백준 1562번 계단 수 JAVA

링크텍스트

설명

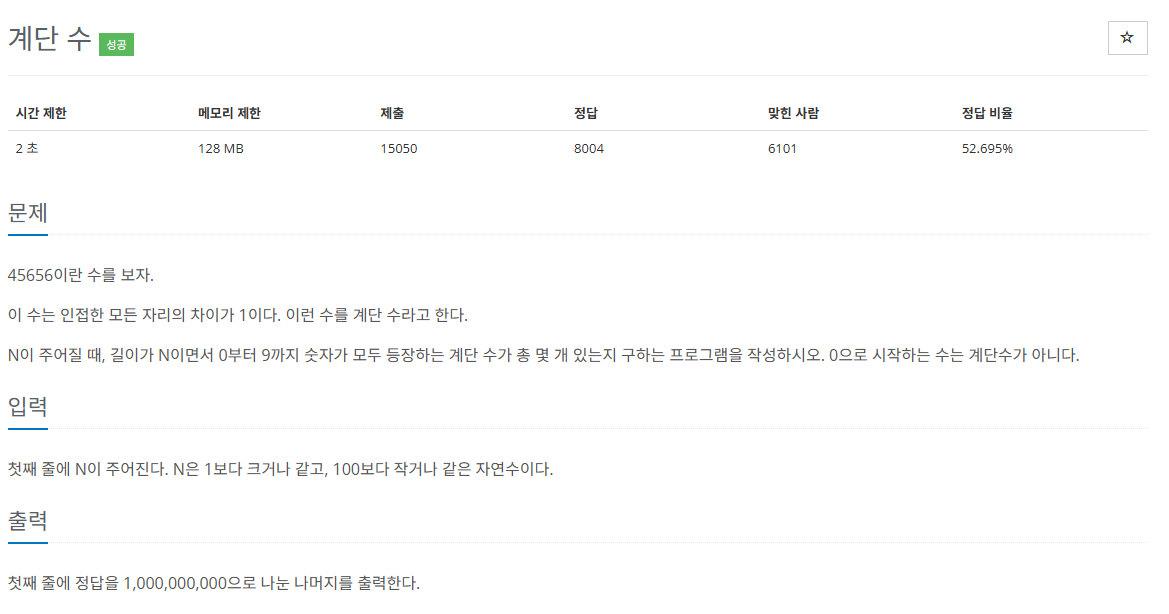
처음으로 도전한 골드 1 문제다. 풀면서 정말 어렵다고 느꼈다. 이 문제를 계기로 앞으로는 설명 아래에 몇 회독했는지를 표시할 예정이다.
이 문제에서는 숫자 0부터 9까지 모든 숫자가 한 번 이상 등장해야 한다. 따라서 N의 길이가 10 미만이면 가능한 경우의 수는 0개다.

비트마스크 1024는 0~9까지 숫자의 등장 여부를 나타내기 위해 선언했다. (2¹⁰ = 1024)
첫 번째 자리에는 1~9만 올 수 있으며, 0으로 시작할 수 없다.
비트마스크에서 1 << digit을 이용해 해당 숫자가 등장했음을 표시한다.
두 번째 자리부터는 j-1 또는 j+1 숫자로만 이동할 수 있다.
이때, 비트마스크(k | (1 << j))를 사용해 해당 숫자가 등장했음을 체크한다.

dp[i][j][k]는 길이가 i이고, 마지막 숫자가 j이며, k 상태(비트마스크)를 만족하는 계단 수의 개수를 의미한다.
특히, dp[n][j][1023]은 길이가 n이고, 마지막 숫자가 j이며, 0~9를 모두 사용한 경우의 개수를 뜻한다.
여기서 1023이 중요한데,
1023 = 0b1111111111
즉, 0부터 9까지 모든 숫자가 최소 한 번 이상 등장한 경우를 의미한다.
시간복잡도: O(N), 공간복잡도: O(N)

회독

• [ x ] 1회
• 2회
• 3회

코드

import java.util.*;
import java.io.*;

class Main {
	public static void main (String[] args) throws IOException {
	    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	    StringBuilder sb = new StringBuilder();

		int n = Integer.parseInt(br.readLine());
		long [][][] dp = new long[n+1][10][1024]; //[숫자 길이][현재 자릿수 숫자][비트마스크]
		int mod = 1_000_000_000;
		
		for(int digit=1;digit<=9;digit++){
			dp[1][digit][1<<digit] = 1;
		}

		for(int i=2;i<=n;i++){
			for(int j=0;j<10;j++){
				for(int k=0;k<1024;k++){
					if(j>0){
						dp[i][j][k | (1 << j)] = (dp[i][j][k | (1 << j)] + dp[i-1][j-1][k]) % mod;
					}if(j<9){
						dp[i][j][k | (1 << j)] = (dp[i][j][k | (1 << j)] + dp[i-1][j+1][k]) % mod;
					}
				}
			}
		}

		long result = 0;

		for(int j=0;j<10;j++){
			result = (result+dp[n][j][1023]) % mod;
		}

		System.out.println(result);
	}
}

참고 글

https://tussle.tistory.com/1143

https://loosie.tistory.com/171

https://seaotter.tistory.com/30