벡터는 크기와 방향을 가지는 단위

벡터에 대한 스칼라 곱이란것은 실수를 * 주는것. 벡터간의 연산

벡터 자체에는 위치정보가 있는 것이 아니다.

3차원 상의 어떤 벡터라도 한 평면에 놓이지 않는 벡터 3개로 표현가능

Affine Combinationt

선형 조합까진 동일
but, 계수들의 합이 1

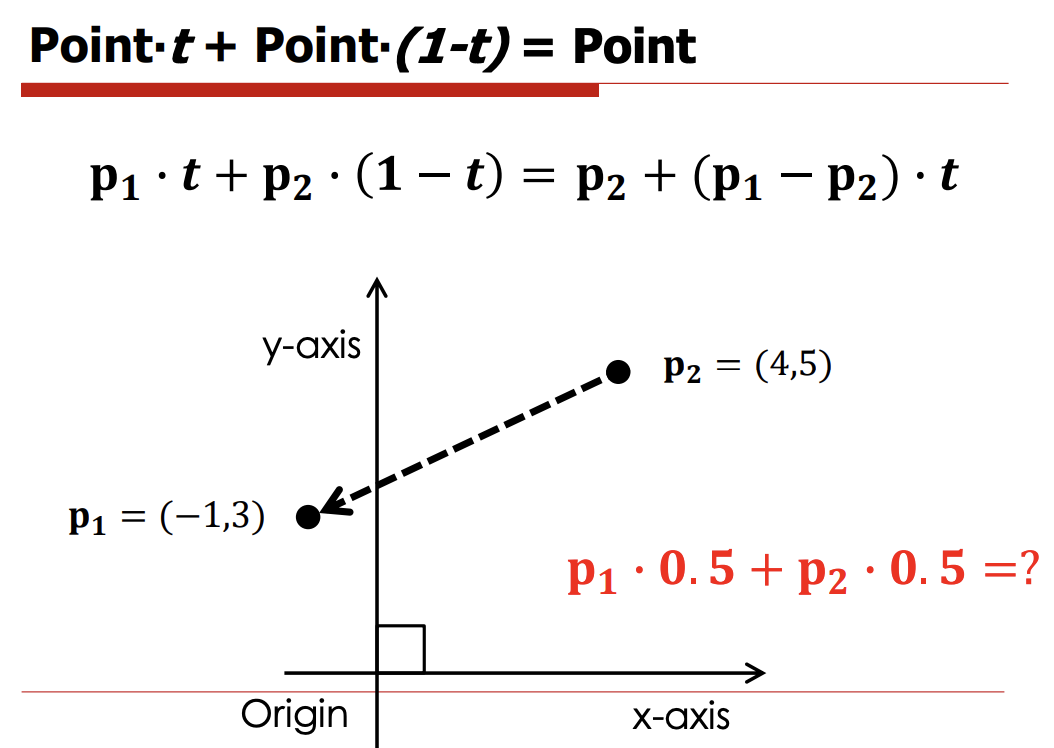
ㄴ 내분을 하거나, 중점을 구하기 용이하다

Convex combination

모든 계수가 0보다 크다.

내분에 가능, 외분은 불가능

벡터와 헷갈리는 것이 Point

둘다 똑같이 좌표값으로 나타내기 떄문에 헷갈릴 수 있다. 그러나 이는 포인터는 결국 위치이다.
위치를 더한다는 것이 의미가 있는가? X
빼는 것은가능한가-> 벡터가 나온다(서로간의 상대적인위치)
Scalar 곱은 의미가 있는가 -> 없다.

그렇기에 이는 서로 다른 타입으로 구현하여 혼용하지 않게 노력해야한다.

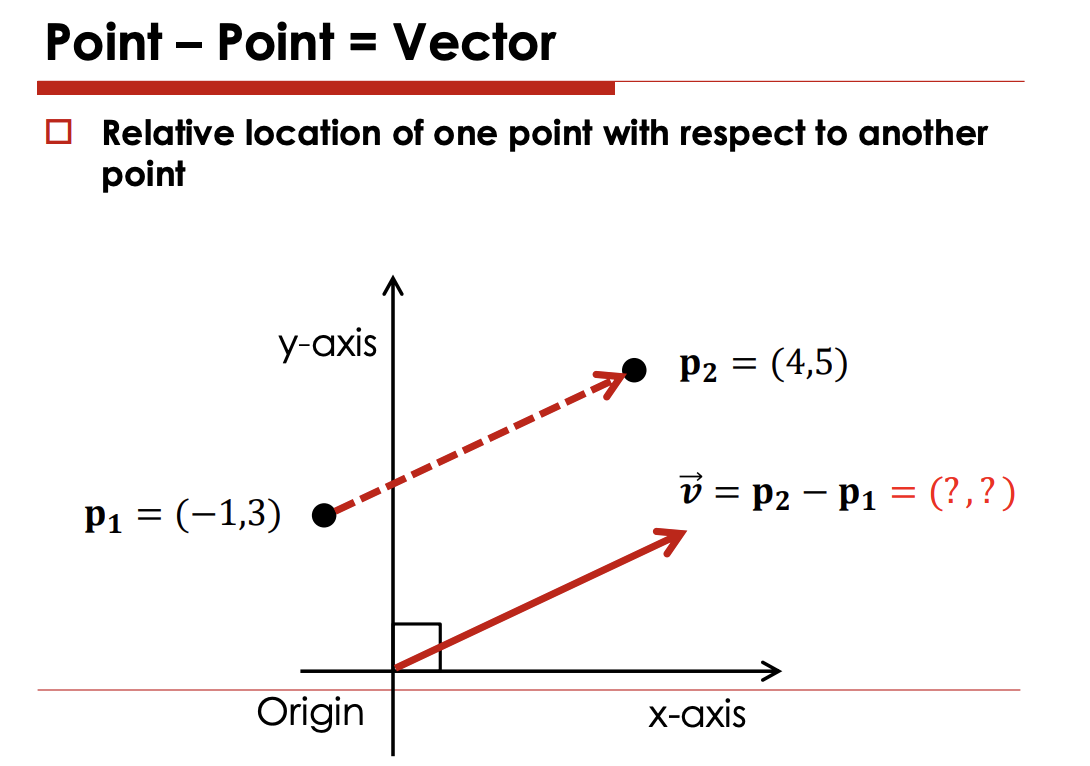
선형 결합중 Affine combination 이 될떄만 기하학적으로 의미가 있다.

내적과 외적

dot product

내적의 결과는 두 벡터의 연산의 결과가 벡터가 아니라

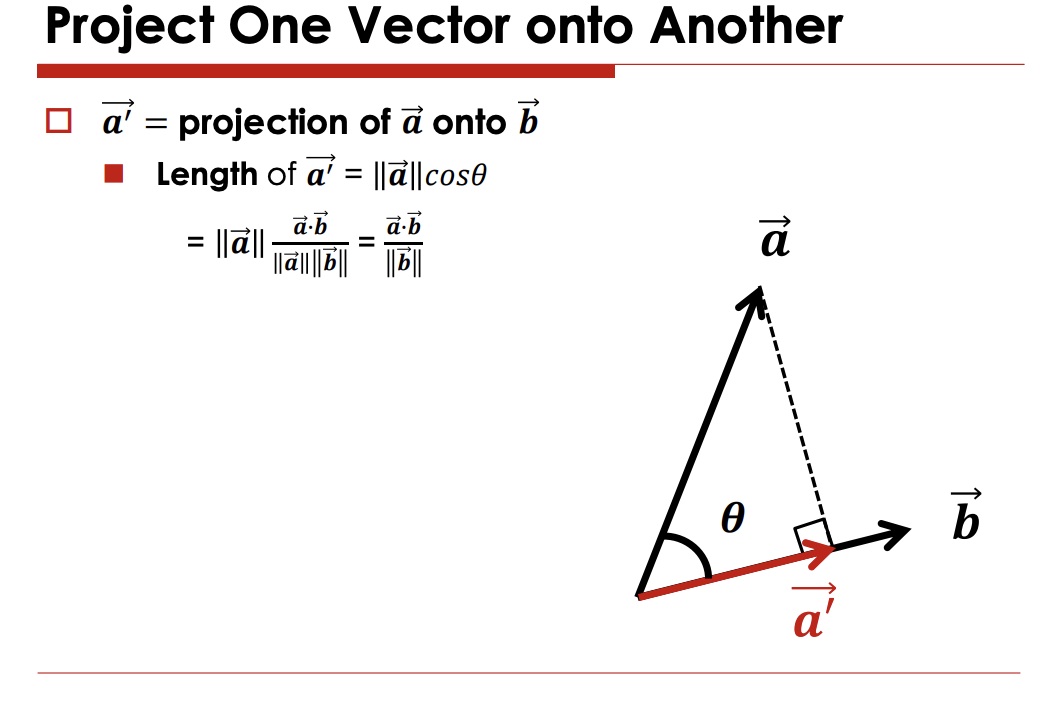
한벡터를 다른 벡터에 프로젝션 - a->b에 수선을 내렸을떄 그 크기를 dot product를 통해 구할 수 있다.
방향은 B벡터가 된다.

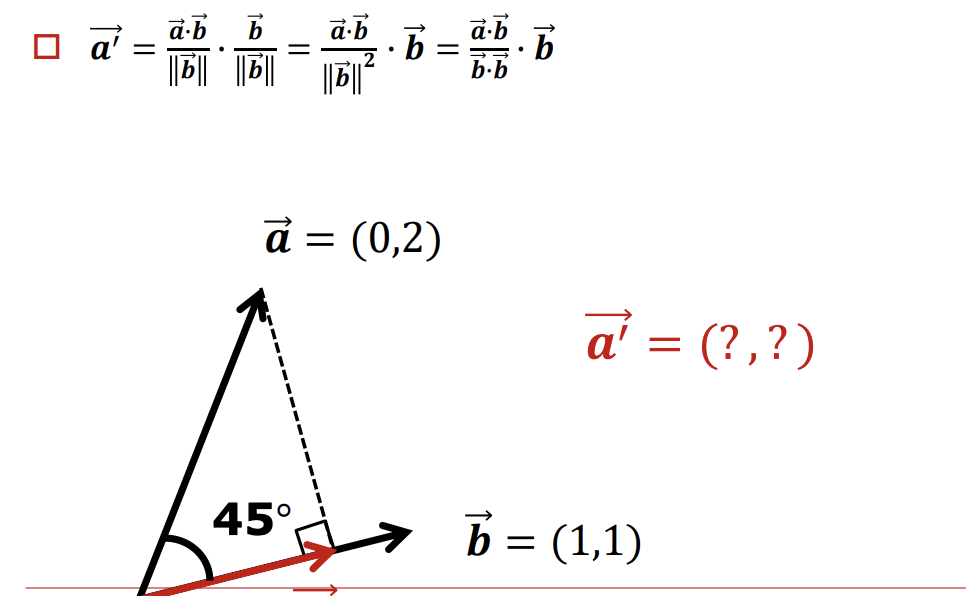
이를 계산하면 1,1정도로 나온다
프로젝션하는 것을 내적을 통해할 수 있어야한다.

이러한 dot product는 서로 다른 두개의 방향이 어떤 관계인지 알 수있다.
내적한 값이 1이라는 것은 일치한다는 것.
방향이 반대인 경우 -1의 값을 가진다 cos180가되기 떄문
직교 여부 cos90도가 되니0

서로 같은 쪽을 보느냐 다른쪽을 보느냐는 0과 1사의 값-> 같은 방향

Cross Product

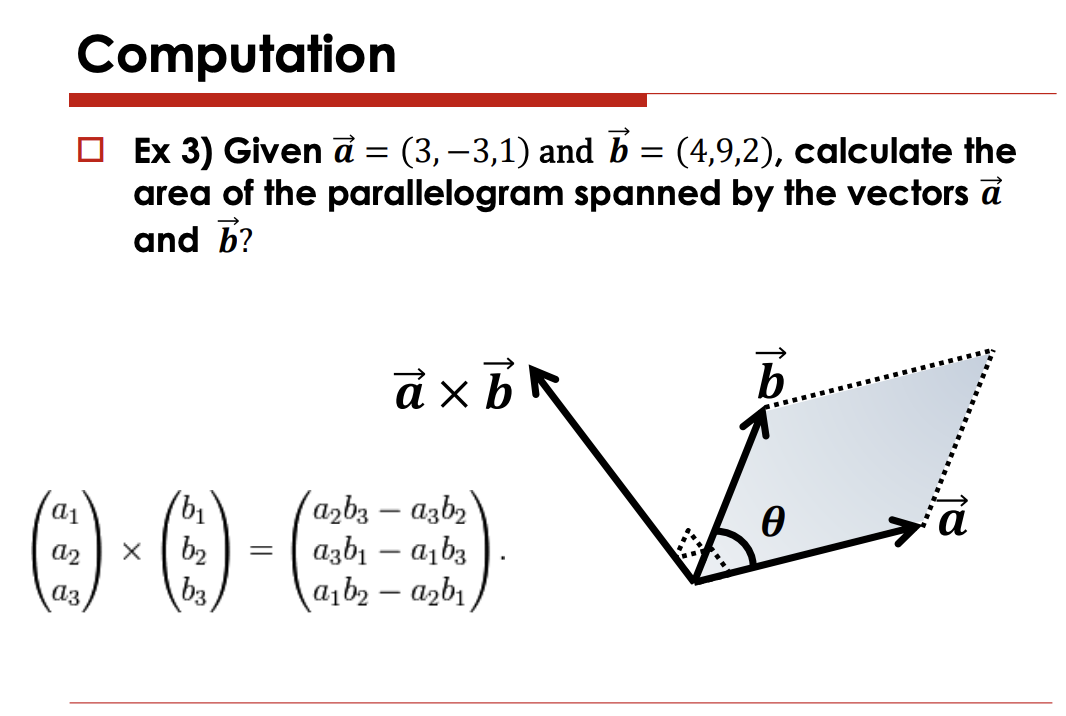
셤에 나오면 푸ㄹ줄알아야함

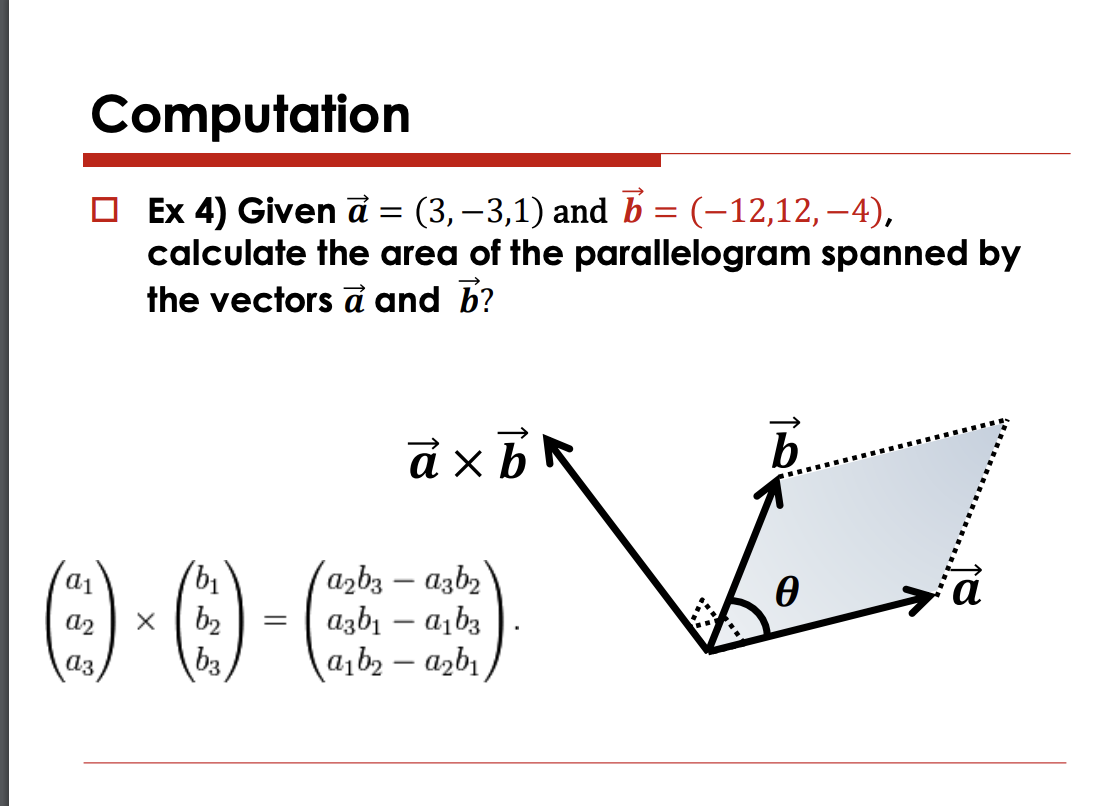
이건 직접 계산안해도 0이 나온다는 걸알아야해 ( -4배 스칼라 곱이기떄문)

Polygon에 법선벡터 방향은 계산을 어떻게하는가 ?
외적을 사용하면 된다.

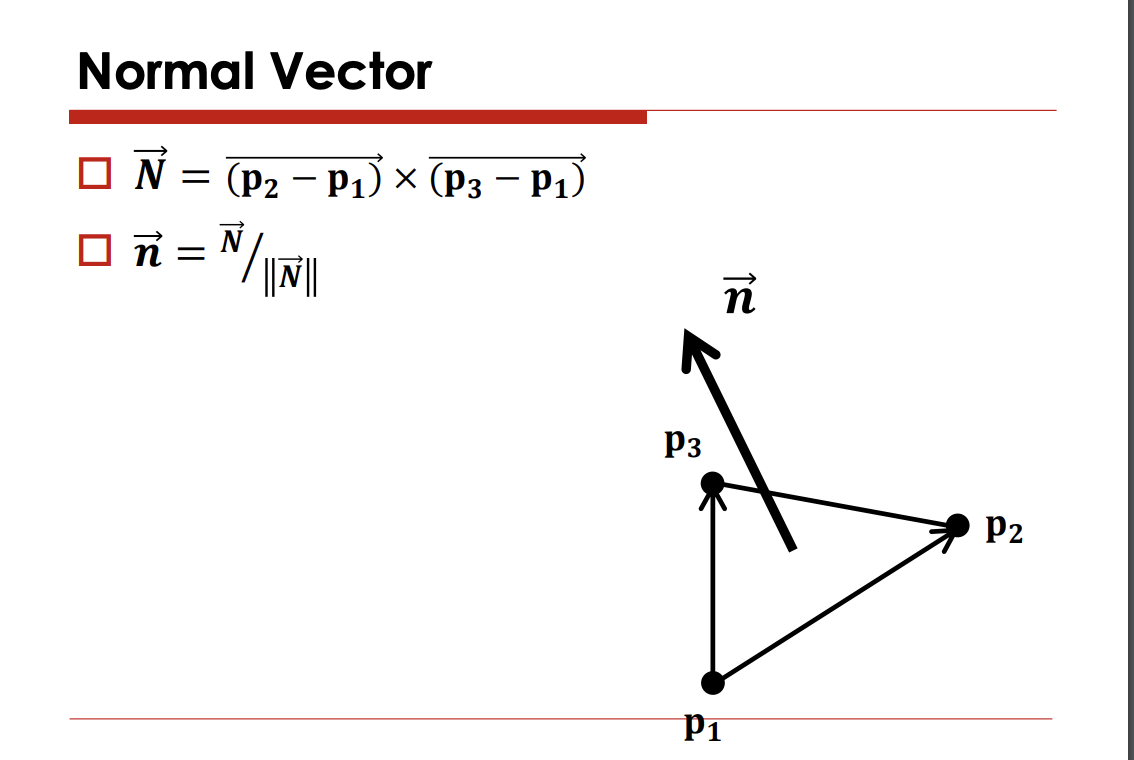
p1->p2
p1->p3 을 외적하면된다
이떄 반드시 정규화 해야한다.

중간고사엔 이런문제들이 나오겠지 미리연습해둬야함