Intro
화면에 비치는 오브젝트에는 다양한 연산이 필요하다.
1. 이동
2. 회전
3. Scalling등
다양한 경우에 행렬이 사용된다.
행렬

M*N의 행렬은 다음과 같이 이야기한다
row 행 - 수평 - 가로줄
column 열 - 수직 - 세로줄
행의 개수: M 열의 개수: N
원소
특정 원소는 다음과 같이 표현한다. ex) i번째 행 j번째 열

Row & Column vector

전치행렬
T로 표시를 하며 행과 열이 뒤바뀐다.
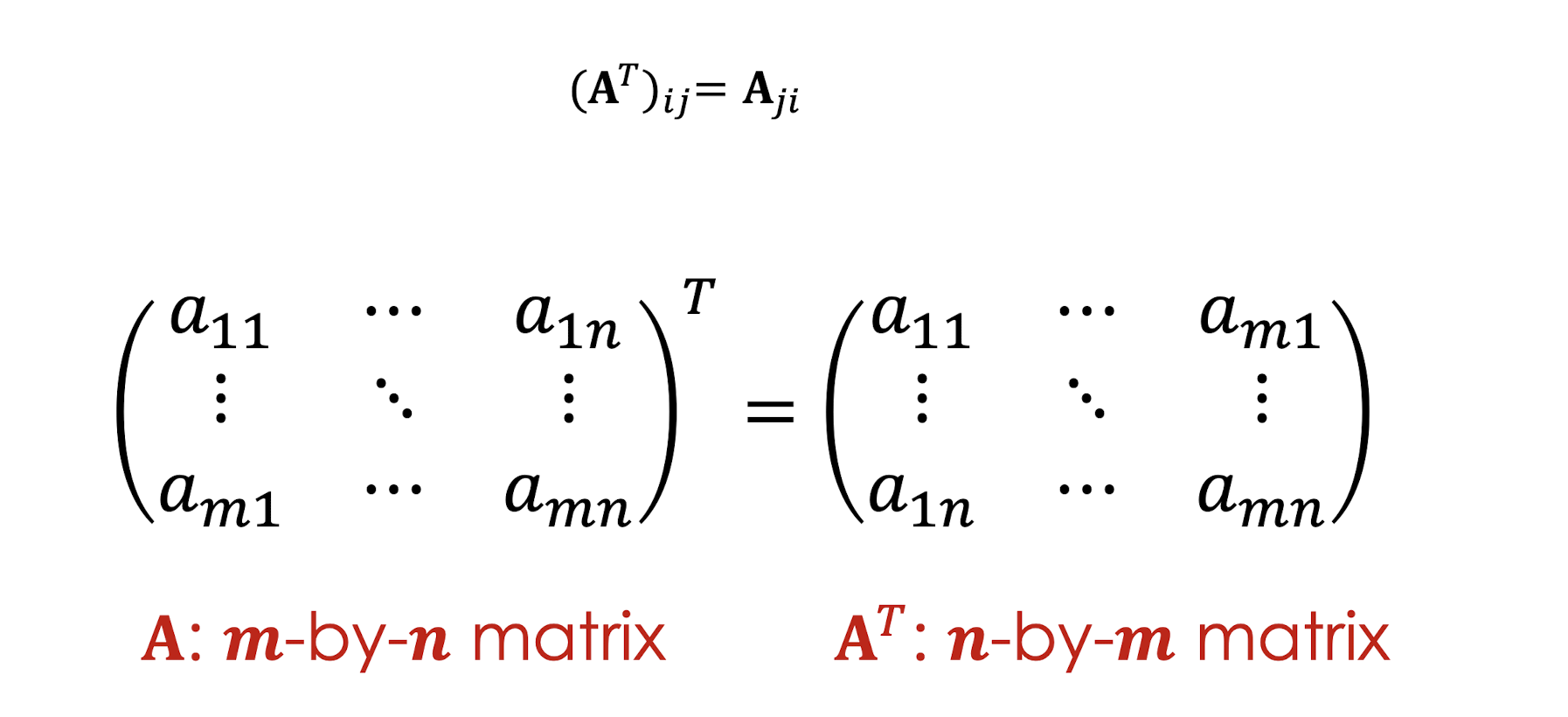
m x n행렬 - 전치행렬 -> n x m행렬
연산
스칼라 곱

모든 원소에 K값을 곱해줌
행렬 합

각 원소에 맞는 원소끼리 합침
행렬의 곱

우선 행렬과 (1개의 열로 이루어진)벡터의 곱을 보자
각 n열과 벡터의 n번째 원소가 곱해져서 앞에 놓인다.
해석1.
행렬과 벡터의 곱은 원래 행의 열벡터를 선형결합하는데 그 계수들이 오른쪽 곱해지는 벡터의 원소가 되는 것이다. 이것이 행렬과 백터의 곱의 정의 이다.
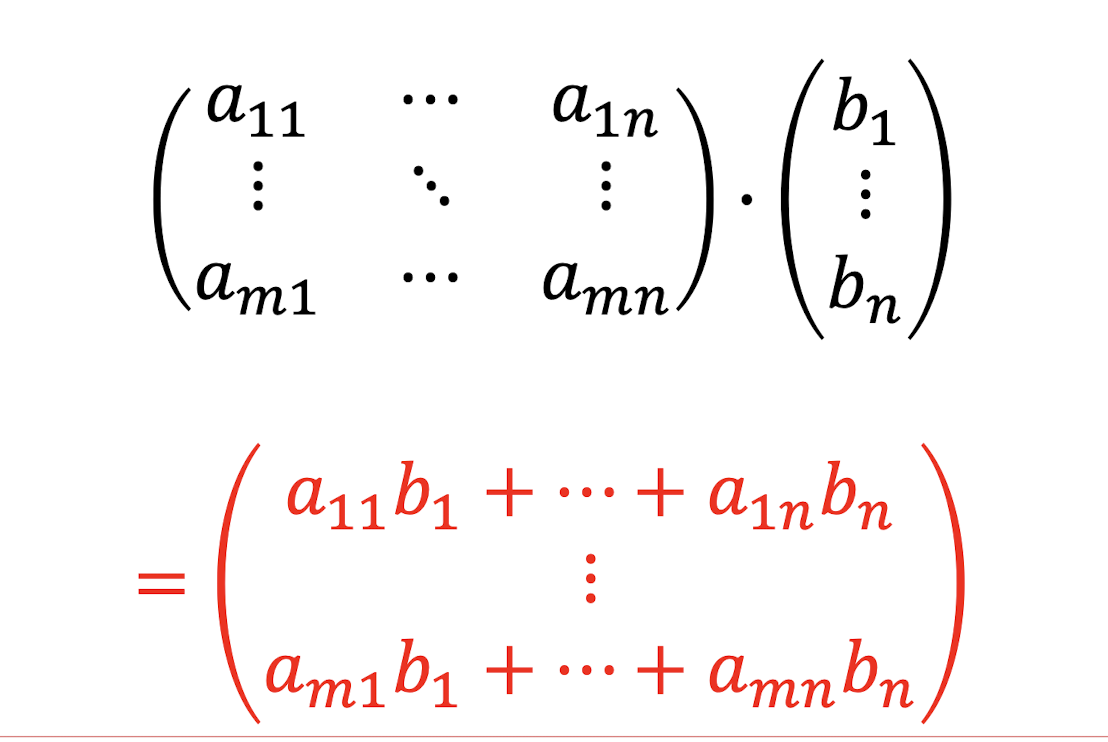
해석 2
내적의 관점으로 해석
각 행렬과 벡터의 곱은 하나의 열백터가 된다 첫번째 행과 벡터간의 내적을 수행한다. 그것이 결과벡터의 첫번쨰 원소가 된다. ...
내적을 통해서 정의한것과 위의 방식으로 내적한 것이 결국 같은 결과를 가진다.
해석하는 방법이 2가지가 있다. 보통 2번째 방법을 계산적인 측면에서 도움이 되기에 많이 배운다.
그러나 개념적으로는 열벡터의 선형결합이 유용한 경우가 많기에 두관점 모두 알면 좋다.
조건
내적의 열의 개수와 곱해지는 백터의 행이 같아야함
행렬 * 행렬
이는 행렬과 행렬의 곱에도 똑같이 적용이 된다.
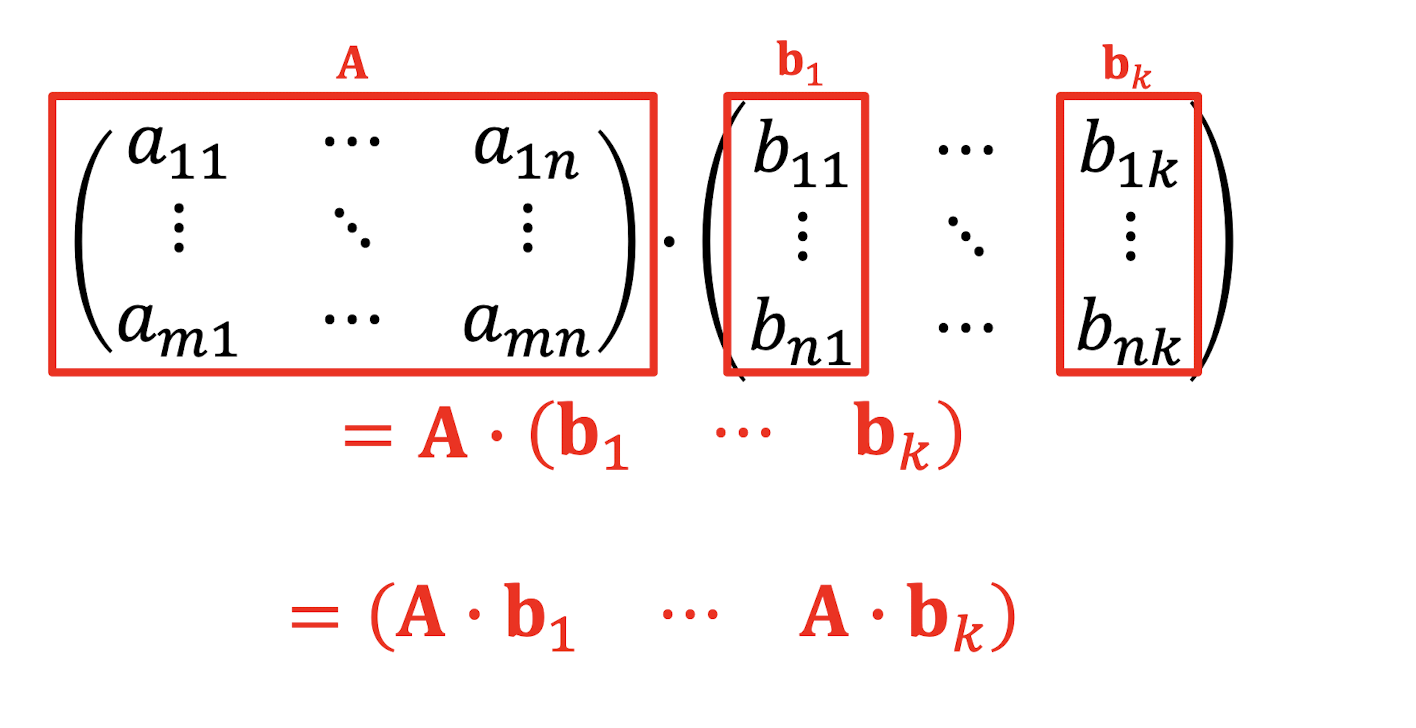
곱해지는 b행렬의 각 열을 하나씩의 백터로 따진다. 그럼 다음과 같은 식이 나오게 된다.
(m x n )행렬에 (n x k)행렬을 곱하면 행의 개수는 M 열의 개수는 K가 된다
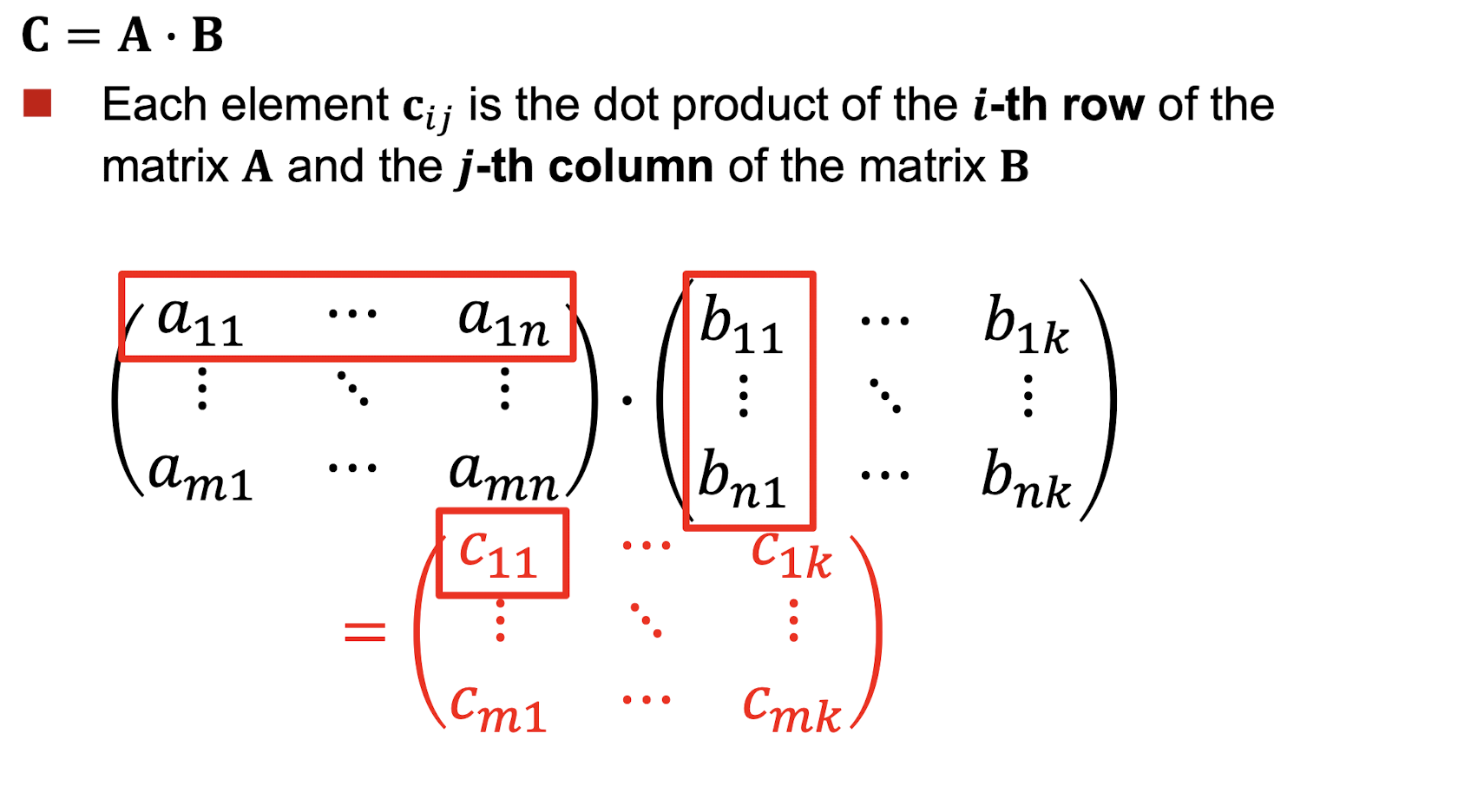
내적 중심의 방식
예시
첫번쨰 행렬의 3행 과 2번쨰 행렬의 4열 내적하면
행렬은 곱하는 순서가 중요하기에 교환법칙 성립
Spuare Matrix
정사각 행렬 M==N인 행렬
Identity Matrix
항등 행렬
항상 곱할떄 같은 행렬이 나오게 된다. 일반적으로 행렬의 곱에는 교환법칙이 성립이 안되나 곱해지는 행렬이 항등 행렬이라면 성립이된다.

Transformation
Modeling transformation
전역 좌표계에서 어디에 배치할지

Viewing transformation
카메라를 어떻게 배치할지
이는 모델링과 상호작용을 크게 가져서 결합해서 생각을 하는 경우가 많다.

Animation
애니메이션은 시간에 따라서 변화하는건데 대게는 위치, 방향, 크기 등이 변화하는 경우가 많다. 우리는 시간에 따라 이러한 공간적 특성이 변화함에 따라 에니메이션을 구성하게 된다.

Transformation 의 정의
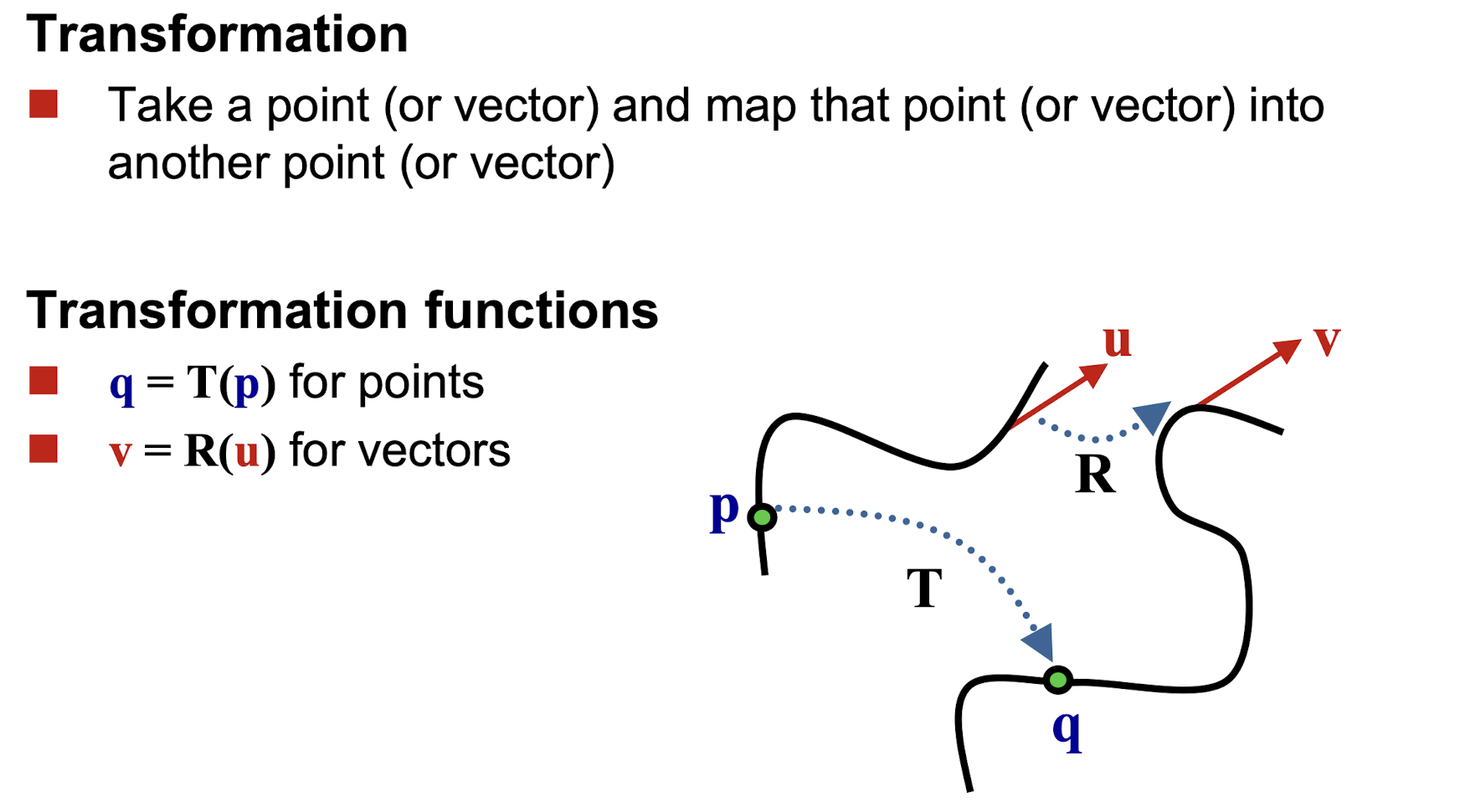
Transformation의 일반적 정의
원래 곡선의 P라는 점이 시간 T가 흐르고 나면 Q로
특정 공간의 포인트를 다른 공간의 포인트로 변환 시키는 것
우리가 보는 변환은 이가 아니라
주로 회전,이동 등을 이야기한다.
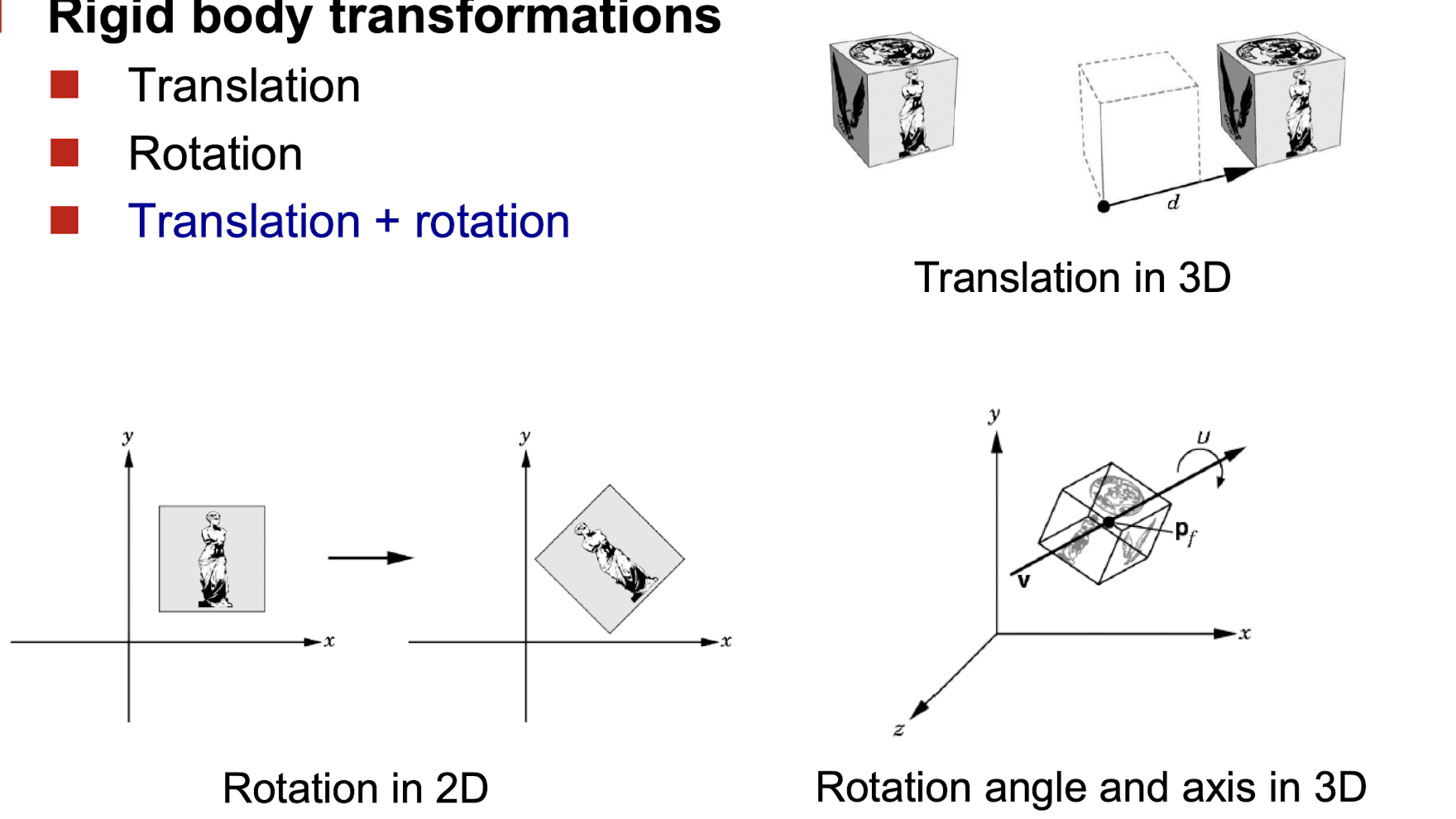
Rigid Body Transformation
강체 - 단단한 물체로
회전과 이동을 생각해볼 수 있다.
Non-Rigid Body
물체의 크기가 고정되지않고 변환 가능
스케일링 크기를 특정 축을 기준으로 크게 만들고 줄이고 할 수 있다
Shearing 은 삐딱하게 기울어지는 것이라 보면된다.

벡터의 선형결합

v1만큼 a v2 만큼 b가 이동 했다고 볼 수 있다.
이가 서로 일치하지 않는 벡터 두개면 다른 벡터가 온다면 표현가능
이런 표현 가능한 벡터를 기저 벡터
이들이 이루는 공간을 선형결합으로 표현 가능한 곳
Linear depent
선형 의존,
하나의 벡터를 다른 벡터의 Scalar 곱으로 표현이 가능한 경우
Linear indepent
선형 독립,
하나의 벡터를 다른 벡터의 Scalar 곱으로 표현이 불가능한 경우
Basis

- 기저 벡터
각 차원을 표현할 수 있는 최소한의 벡터
표현 가능한 공간을 Span 이라고한다.
- Orthonormal Basis
서로 직교하는 단위 기저 벡터
n차원은 n개의 Orthnormal Basis 만 있으면 표현 가능
Ortho-직교 normal- 단위벡터
활용- 데카르트 좌표계 , 카르테시안 좌표계

Basis 가 동일하다면
특정 좌표를 표현할 수 있는 식은 하나밖에 없다.
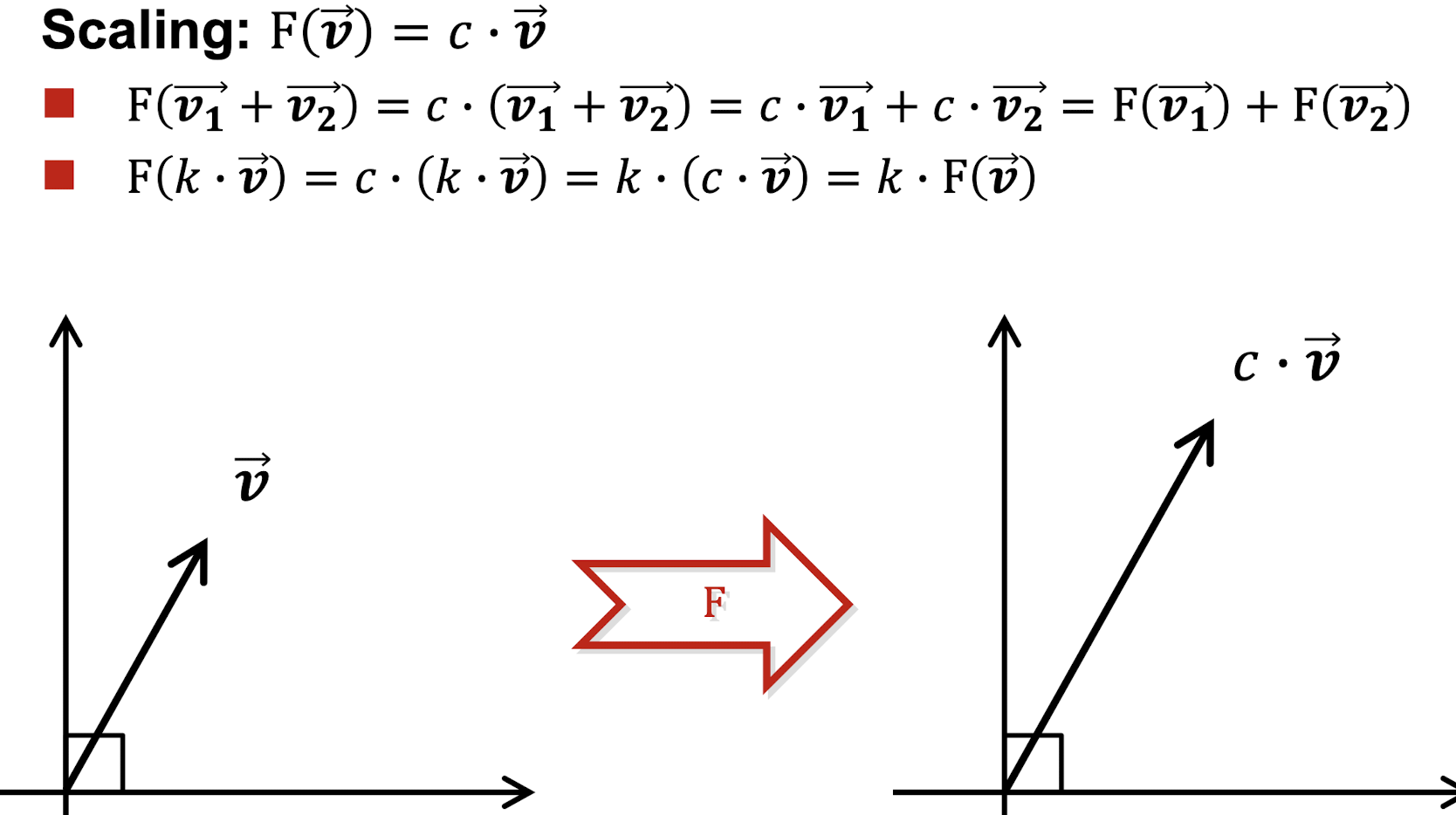
Linear Map

함수에 어떤 벡터 A 를 넣으면 B라는 벡터가 나와야한다.
뒤의 2가지 조건을 만족해야하는데 이는 선형성을 만족하는 조건이다.
이러한 조건을 만족하는 함수를 선형 사상(Linear map) 이라한다.
결국 기저벡터의 선형결합으로 표현이 가능하다.
확인시
1.더하기에 의해 확장 가능한지
2.스칼라 곱에 의해 확장이 가능한지
예시
아래에 따라 F(V)는 Linear
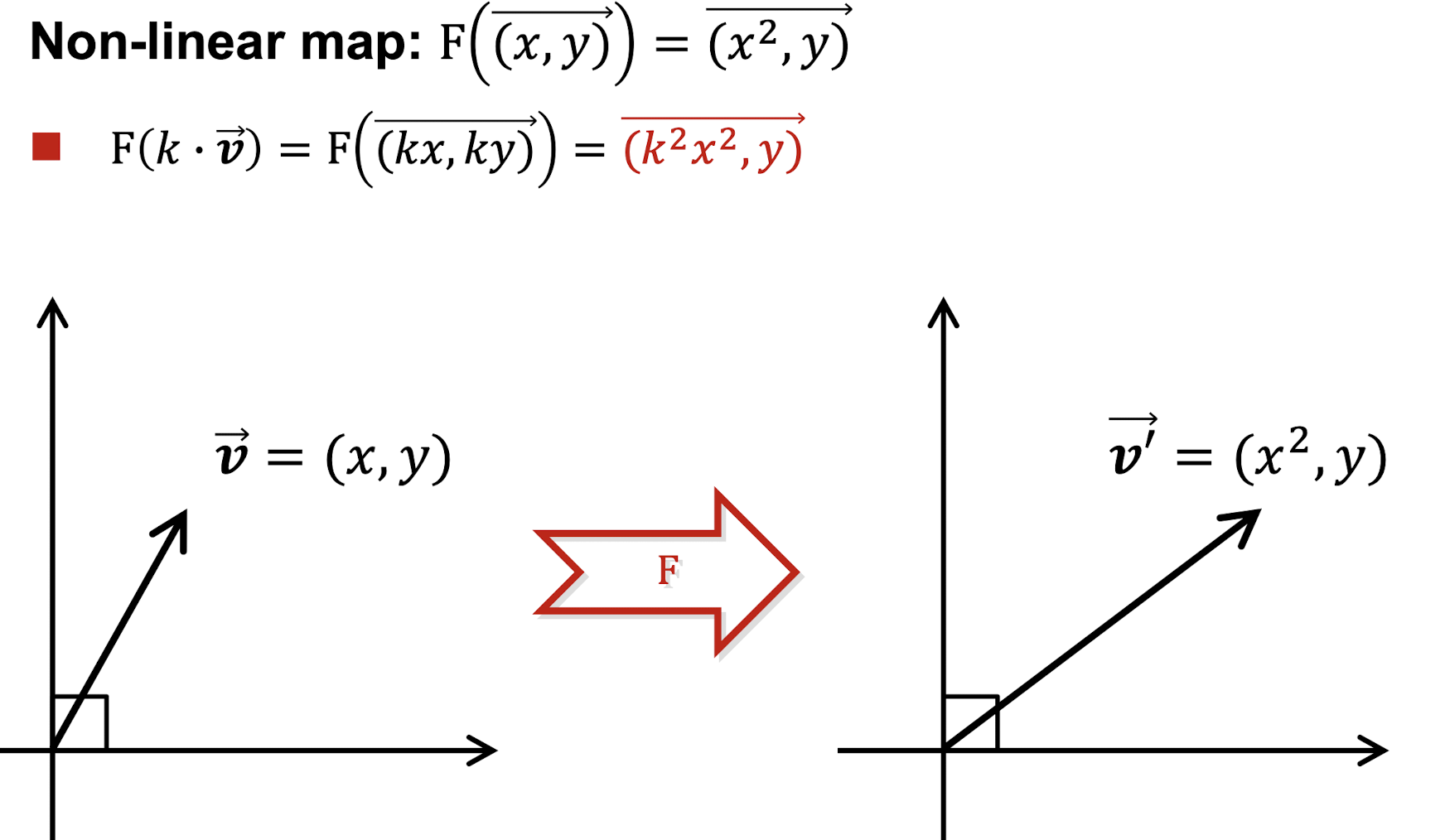
반례
아래는 곱셈에 해당 X 비선형