참고: Calibrate라는 영단어는 그 사전적 의미로는 “(계기 등에) 눈금을 매기다”라는 뜻입니다.

이 리뷰는 2024년 8월 21일 열린 인공지능 스터디 발표를 위해 작성한 논문 리뷰입니다. 왠지 빨리 설명을 마칠 수 있을 것 같은 자신이 들어서 후다닥 설명할 목적에 맞추어 적었던 기억이 있습니다.

https://arxiv.org/pdf/1706.04599

Abstract

• Confidence calibration―예측 확률이 실제 참일 확률과 일치하는 것—은 많은 분야에 응용에서 중요하다.
  • 최근의 뉴럴 네트워크들은 과거의 것과 다르게 poorly calibrated됨을 발견했다.
  • depth, width, weight decay, batch normalisation이 calibration을 높이는 중요한 요소임을 관찰했다.
• 이미지 분류나 문서 분류에서의 SOTA 구조(모델)에 대해 기존의 calibration 후처리 방법들을 평가했다.
  • temperature scaling이라는 단일 파라미터 방법이 많은 데이터셋에서 calibrating에 있어 놀랄 정도로 효과적임을 알아냈다.

1. Introduction

• 최근의 딥러닝 모델들은 성능이 매우 좋아서, (그 이유만으로) 신뢰가 증대되고 있다.
• 현실 세계에 적용할 때는 분류 모델이 정확해야 할 뿐만 아니라, 어느 정도로 부정확할 것인지의 확률도 알아야 한다.
  • 가령 딥러닝을 헬스케어에 적용할 때, 모델의 confidence score가 낮으면 인간 의사에게 통제를 넘겨야만 할 것이다.
  • 더 정확히는, 뉴럴 넷은 예측값에 대해 “calibrated” confidence를 제공해야 한다.
    • 구체적으로, 예측 값으로 나온 클래스의 라벨이 실제 ground truth의 정확도와 일치해야 한다.
• Calibrated confidence estimation은 모델의 해석 가능성에서도 중요하다.
  • 인간은 자연적으로 가능성에 대한 직관이 있기 때문에, confidence score를 잘 추정하는 것은 사용자와의 신뢰 형성을 위한 정보를 보충한다.
    • 특히 뉴럴 넷의 의사 결정은 자주 해석하기 어렵다.
• 확률 값을 잘 추정하는 것은 다른 확률적 모델(probabilistic model)에 포함시키는 것을 유용하게 만든다.
  • 음성 인식에 언어 모델을 넣거나, 카메라 정보에 객체 탐지 모델을 넣거나 하는 식
  • 2005년 연구에서는 뉴럴 넷이 대체로 이진 분류에서 well-calibrated되어있다는 연구가 있었다.
• 10년 전 모델에 비해 현재의 모델은 의심의 여지가 없이 정확도가 더 높지만, 우리도 현대의 뉴럴 네트워크가 더 이상 well-calibrated되지 않았음을 발견하고 놀랐다.
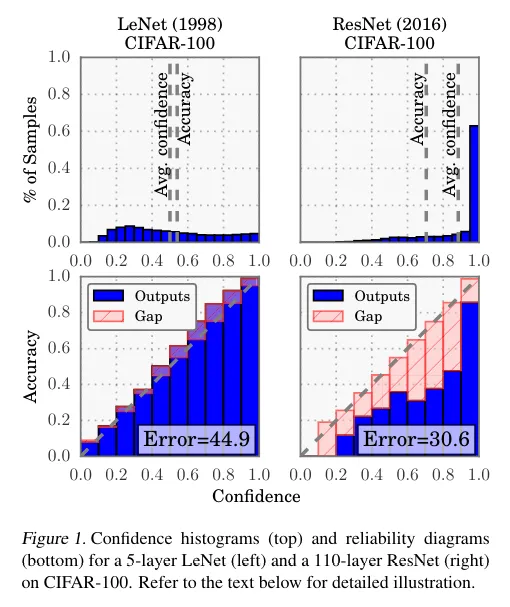
  • Figure 1은 5개의 레이어가 있는 LeNet과 110개의 레이어가 있는 ResNet을 CIFAR-100 데이터셋을 학습한 것을 비교하는 사진이다.
    • LeNet의 평균 confidence는 거의 accuracy와 일치하는데, ResNet의 평균 confidence는 accuracy를 훌쩍 뛰어넘는다.
    • 그 아래에 있는 “Reliability Diagram”을 보면, LeNet은 정확도는 떨어질지언정 모델의 예측 확률과 실제 확률이 일치하는 반면(곧 설명이 나옴. 파란 막대가 대각선을 따라 있어야 함), ResNet은 정확도가 더 좋지만 confidence score와 일치하지 않는다.
• 이 논문의 목표는 왜 miscalibration이 일어나는지, 어떤 방법이 이 문제를 보완할 수 있을지 앚는 것이다.
  • 컴퓨터 비전과 자연어 처리 태스크에 대해 실험을 진행
  • temperature scaling(이라고 논문 저자들이 부르길 원하는) 방법은 구현하기도 쉽고 가장 효과적이다.
    • LLM을 연구하다 보면 temperature라는 속성을 보게 되는데 이 논문에서 비롯된 것입니다.

2. Definitions

(이 논문에서는 신경망의 지도학습 기반 분류에 대한 것임)

• input $X$와 output $Y \in \{ 1,2,...,k \}$는 확률변수이며, 그 ground truth의 결합확률분포 $\pi(X, Y)=\pi(Y|X)\pi(X)$를 따른다. $h$는 뉴럴 네트워크를 나타내고 $h(X)=(\hat Y, \hat P)$로 나타나며 여기서 $\hat Y$는 클래스 예측 결과이고 $\hat P$는 모델의 예측 확률(confidence score)이다.
• 우리는 모델의 예측 확률 $\hat P$가 “calibrated”되기를 원하며, 이를 직관적으로 표현하면 실제 확률을 잘 표현하는 것을 뜻한다.
  • 100개의 예측 결과가 있고, 각각의 confidence가 0.8이면, 실제로도 80%가 맞게 분류된 것을 의미한다.
• 논문에서는 perfect calibration이라는 이상적인 한 가지 상태를 내세우는데, 그 정의는 다음을 만족하는 것이다. (실제로 유한 개의 샘플로 달성 및 만족 여부 확인은 불가능)
  $\mathbb{P}(\hat Y = Y |\hat P=p)=p,\ \forall p \in [0,1]$

Reliability Diagrams

• 모델의 Expected accuracy를 confidence의 함수로 생각하여 나타낸 그림이다.
  • 모델이 perfectly calibrated되어 있다면 diagram은 항등함수여야 한다. (조금이라도 벗어나있다면 miscalibration을 뜻함)
• 유한 개의 샘플로 그 값들을 추정하려면, 예측 값들을 M개의 구간(bin)으로 나눠서 각각의 bin 내에서 계산해야 한다.
  • 예측 확률이 구간 $\left(\frac{m-1}{M}, \frac{m}{M}\right]$안에 들어오는 샘플의 집합을 $B_m$이라 하자. $B_m$의 accuracy는 다음처럼 정의한다.
    $acc(B_m) = \frac{1}{|B_m|}\sum_{i \in B_m} 1(\hat y_i = y_i)$
    • $\hat y_i$, $y_i$는 예측, 실제 클래스 라벨이다. $acc(B_m)$은 $P(\hat Y = Y | \hat P \in I_m)$의 불편추정량(기댓값이 모수와 같음)이자 일치추정량(표본이 많아질수록 모수에 근접함)이다.
  • $B_m$에서의 평균 confidence는 다음처럼 정의한다.
    $conf(B_m) = \frac{1}{|B_m|}\sum_{i \in B_m} \hat p_i$
    • $\hat p_i$는 i번째 샘플에 대한 confidence 값이다.
  • perfectly calibrated model은 모든 $m \in \{ 1, … , M \}$에 대하여 $acc(B_m) = conf(B_m)$이어야 한다.
  • 각 acc와 conf는 perfect calibration의 정의에서 각각 좌변과 우변을 approximate한다.
• 주의: reliability diagram에서 각각의 bin에 샘플의 개수 비율이 같을 필요는 없다. 그래서 “얼마나 많은 샘플이 calibrated되었는지”를 말해주는 것은 아니다.

Expected Calibration Error (ECE)

• Reliability Diagram은 시각적 도구로서 훌륭하지만 이를 요약하는 통계량이 있으면 편리할 것이다.
• Miscalibration을 나타내는 한 방법은 confidence와 accuracy 간 차이의 기대값을 생각하는 것이다.
  $\mathbb{E}_{\hat P}[|\mathbb{P}(\hat Y=Y|\hat P = p) - p|]$
  • 이 값을 근사적으로 구하는 방법은 reliability diagrams에서와 같은 방법으로 여러 개의 bin으로 나눈 다음에 각 bin에서의 가중평균을 취하는 것이다. (충분히 큰 샘플 수 n에 대해)
    $ECE = \mathbb{E}_{\hat P}[|\mathbb{P}(\hat Y=Y|\hat P = p) - p|] \\ = \int_0^1 |\mathbb{P}(\hat Y=Y|\hat P=p)-p|dF_{\hat P}(p) \\ \approx \sum_{m=1}^M |\mathbb{P}(\hat Y=Y|\hat P=p_m)-p_m| \mathbb{P}(\hat P \in I_m) \\ \approx \sum_{m=1}^M \frac{|B_m|}{n}|acc(B_m)-conf(B_m)|$
  • acc와 conf의 차이는 Figure 1의 Reliability Diagram에서의 빨간색 막대기를 뜻한다.
• 이 값(ECE)를 calibration을 측정하는 주된 메트릭으로 사용할 것이다.

Maximum Calibration Error (MCE)

• 특정 분야에서는, acc와 conf 간 차이를 작게 하되, 다음 식을 최소화하여 최악의 경우를 최소화하는 것이 더 중요할 수 있다.
  $MCE = \max_{p \in [0,1]}|\mathbb{P}(\hat Y=Y|\hat P = p) - p| \\ \approx \max_{m \in \{1, ...,M\}} |acc(B_m)-conf(B_m)|$
• MCE는 가장 큰 calibration gap(빨간 막대기)를 뜻하며, MCE는 전체 gap의 가중평균을 의미한다.
  • perfectly calibrated classifier는 $MCE=ECE=0$이다.

Negative log likelihood (NLL)

• 확률 모델의 질을 측정하는 데에 표준적인 방법으로 자리잡았다.
  • 딥러닝의 맥락에서는 “크로스 엔트로피”라고도 부른다.
• 확률모델 $\hat \pi (Y|X)$와 n개의 샘플이 있으면 그것의 NLL은 다음처럼 정의된다.
  $\mathcal{L} = -\sum_{i=1}^{n} \log(\hat \pi(y_i|\bold{x}_i))$
• NLL이 최소화되는 필요충분조건은 $\hat \pi (Y|X)$가 ground truth의 분포 $\pi (Y|X)$를 완벽히 보존할 때이다.

3. Observing Miscalibration

• 근 몇 년 간 뉴럴 네트워크의 훈련 방식이나 구조는 많이 진화했는데…
  • 그 중 몇 가지 기법은 calibration을 저해하는 현상을 발견했다.
  • 다만 인과 관계에 대해 여기서 직접 논할 수는 없다.

Model capacity

• 최근 몇 년 간 신경망의 model capacity는 엄청나게 늘어났다.
  • 최근 연구 왈: 작은 모델보다 깊고 넓은 모델이 더 일반화 성능이 높으면서도, 훈련 세트에 쉽게 적합될 수 있는 용량이 있다.
• 그렇게 depth, width 늘리는 게 예측 오류를 줄일지라도 calibration에는 좋지 못하다.
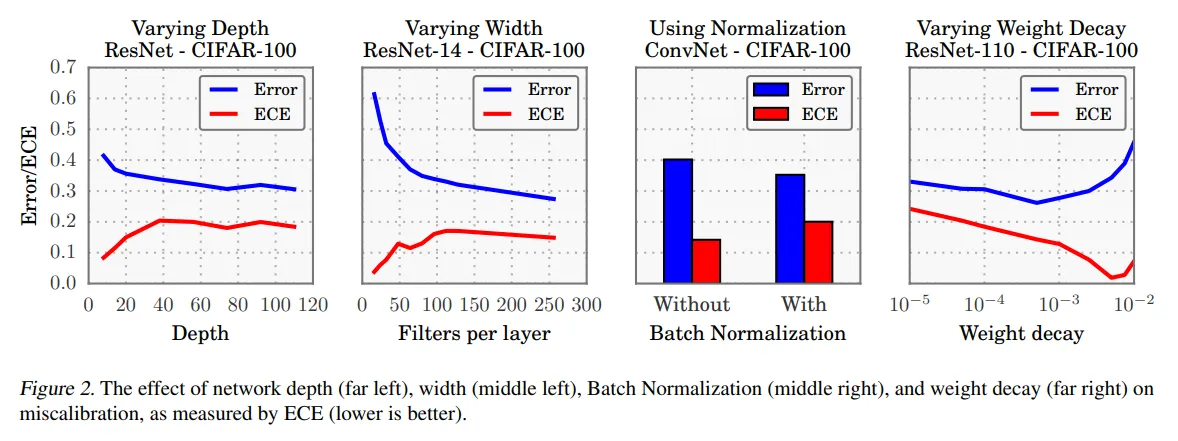
• Figure 2 맨 왼쪽에는 CIFAR-100을 ResNet에 학습한 결과
  • 첫 번째 그래프는 각 레이어에 64 convolution layers를 맞춰줬고, 두 번째 그래프는 14개의 레이어로 고정하였다. (통제 변인)
• ECE가 model capacity가 커짐에 따라 점진적으로 커진다.
• 훈련 도중 모델이 얼추 훈련 샘플을 맞추게 되면, 예측의 confidence를 높이며 NLL을 한 층 더 낮출 수 있을 것이다. (의문점 - confidence를 높인다고?)
  • 모델의 크기가 커지는 것은 NLL 최적화를 덜 하게 만들며, 평균적으로 모델이 overconfident하게 될 것이다.

Batch Normalisation

• 은닉층 내에서 일어나는 “내부 공변량 변화”를 최소화하기 위한 기법
  • 배치 정규화는 훈련 시간에서도 유리하고 다른 규제를 덜 해도 돼서 좋다고 알려짐
  • 몇 경우에는 모델의 정확도 향상에서도 좋다고 알려짐
• 논문 저자는 배치 정규화를 사용한 논문이 더 많이 miscalibrated되는 경향성을 발견했다.
  • Figure 2의 세 번째 사진을 보면 레이어 6개짜리 ConvNet의 calibration이 더 좋지 않은 것을 볼 수 있다.
  • 이 결과는 여러가지 하이퍼파라미터 값(높고 낮은 learning rate 등…)에도 불구하고 같은 양상으로 나타난다.

Weight Decay

• 신경망의 규제 기법
  • Learning Theory에서는 규제가 오버피팅을 막는 데에 필요하다고 하는데, 특히 model capacity가 증가할 수록 그렇다.
  • 최근 연구를 보면 L2 규제를 적용한 모델이 일반화 성능이 좋다.
• weight decay를 작게 하여 학습했을 때 calibration에 나쁜 영향을 준다.
  • weight decay를 많이 한다고 해서 calibration에 나쁜 영향을 주지는 않는다.

NLL

• model의 calibration을 간접적으로 측정하는 데 쓸 수 있다.
• 논문 저자는 NLL과 accuracy가 따로 노는 것을 봤는데, Figure 2의 miscalibration을 설명해줄 수 있을지도 모른다.
  • 뉴럴 네트워크는 0/1 loss에 오버피팅되지 않고도 NLL에 오버피팅될 수 있다.
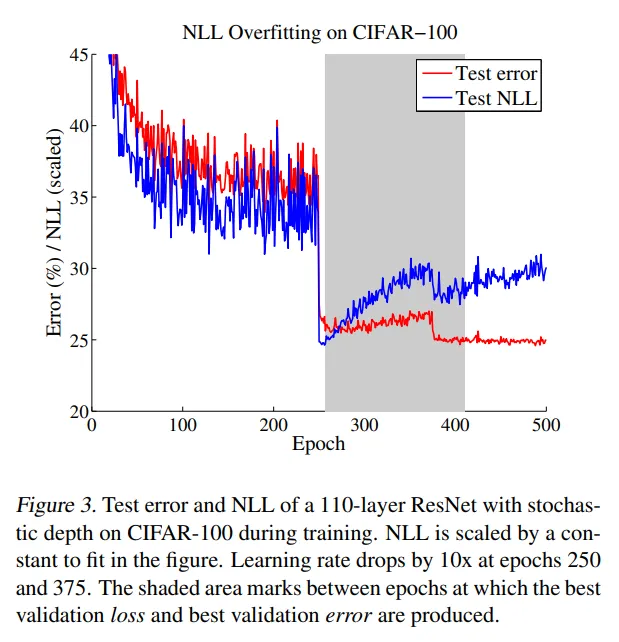
    • miscalibrated한 모델의 학습 곡선에서 이러한 양상을 볼 수 있다.
  • Figure 3을 보면 error와 NLL이 동시에 250에포크에서 (학습률이 낮아질 때) 떨어지지만, NLL은 overfit한 상태로 남는다.
  • 신기하게도 NLL에 오버피팅된 것은 분류 정확도에 좋은 영향을 준다.
    • CIFAR-100에서, NLL에 오버피팅이 시작될 때 테스트 에러가 29%에서 27%로 감소
• 다시 말해, 잘 모델링된 확률을 대가로 더 높은 분류 정확도를 얻는 것이다.
  • 대규모 신경망의 일반화 성능을 설명하는 최근 연구와 연관지을 수 있다.
    • Zhang et al. (2017)에 따르면, 큰 모델에 적은 규제를 했을 때 일반화 성능이 떨어진다는 기존 지식에 반하는 결과를 얻었다.
    • NLL과 0/1 loss 간의 분리성은, capacity가 높은 모델이라도 꼭 오버피팅에 면역이 있다는 것은 아님을 의미하며, 그 대신 오버피팅이 나타나는 것은 확률적 오류에서이지, 분류에서의 오류가 아니다.

4. Calibration Methods

논문에서 몇 가지 calibration method (’눈금을 맞추는’ 방법)를 언급하고 있으나, 우리는 논문에서 중요하게 여겨지는 한 가지에만 주목하겠습니다.

4.1 Calibrating Binary Models

• 우선 이진 분류에서의 모델을 생각한다.
  • i.e. $\mathcal{Y} = \{0, 1\}$
• 편의성을 위해서, 여기서 모델의 출력은 positive class에 대한 confidence라고 가정한다.
  • $\hat p_i = \sigma (z_i)$

Histogram binning

Isotonic regression

Platt scaling

• 다른 방법과 다르게 모수적(parametric) 방법이다.
• 실수 파라미터 a, b를 학습하는데, calibrated된 예측 확률 값으로 $q_i = \sigma(az_i + b)$를 출력한다.
  • 파라미터 a, b는 validation set에서의 NLL loss를 최적화하여 얻는다.

4.2 Extension to Multiclass Models

• K>2개가 넘는 클래스의 분류 문제에서는, 원래의 식으로 돌아온다.
• 신경망은 각 입력 $\bold{x}_i$에 대해 클래스 예측 $y_i$와 confidence score $\hat p_i$를 출력한다. 이 경우 network logit $\bold{z}_i$는 벡터이고, $\hat y_i = \argmax _k z_i ^{(k)}$이며, $\hat p_i$는 전형적으로 softmax 함수를 이용해 얻어진다.
  $\sigma _{SM} (\bold{z}_i)^{(k)} = \frac{\exp(z_i^{(k)})}{\sum_{j=1}^{K}\exp(z_i^{(j)})},\ \hat p_i = \max _k \sigma _{SM}(\bold{z}_i)^{(k)}$
  • 우리의 목표는 calibrated된 confidence $\hat q_i$와 분류 예측 $\hat y'$를 찾는 것이다.

Extension of binning methods

Matrix and vector scaling

Temperature scaling

• Platt scaling의 가장 간단한 확장판이다.
  • 단 한 개의 파라미터 $T>0$를 사용한다.
• 새로운 confidence prediction의 값은 다음처럼 정해진다.

• 여기서 $T$는 temperature라고 불리는 것이다.
  • $T>1$이면 softmax를 “soften”한다(output의 entropy를 올린다).
  • $T → \infty$이면 확률 $\hat q_i$는 $1/K$로 수렴한다.
  • $T=1$이면 원래의 예측 확률 $\hat p_i$를 보존한다.
  • $T → 0$ 이면 확률이 한 점으로 모일 것이다(i.e. $\hat q_i = 1$).
• $T$는 validation set에서 NLL에 대해 최적화하여 얻는다.
• $T$라는 파라미터가 softmax function의 maximum을 바꾸지는 않는다.
  • 그래서 $\hat y'$가 바뀌지는 않을 것이고, 따라서 모델의 accuracy에는 영향을 주지 않는다.
• Temperature scaling은 knowledge distillation, statistical mechanics 등에서 쓰이지만 확률 모델을 calibrating하는 데에 쓰인 이전 사례는 없다.

4.3 Other Related Works

5. Results

• Section 4의 방법들을 이미지 분류와 문서 분류 모델에 적용했다.
  • 이미지 분류에 대해서는 6개의 데이터셋에 대해 적용했다.
    • ResNet, ResNet with stochastic depth(SD), Wide ResNets, DenseNets 등과 같은 state-of-the-art 모델을 학습했다.
  • 문서 분류에 대해서는 4개의 데이터셋에 대해 적용했다.
    • Deep Averaging Networks(DANs), TreeLSTMs을 학습함

Calibration Results

• Model Calibration을 ECE로 측정하였음 (M=15 bins)
• 대부분의 데이터셋과 모델이 ECE 기준 4~10% 정도의 miscalibration을 보인다.
  • 이는 모델의 구조와 상관없이 그렇다.
    • CNN에서도 그렇고, RNN에서도 그렇고, DAN에서도 그렇고…
    • 예외도 있긴 하다. (SVHN, Reuters는 ECE가 1% 미만으로 나옴)
• 가장 중요한 관찰: temperature scaling은 눈에 띄게 간단함에도 불구하고 놀라운 효과성을 보인다.
  • Temperature scaling은 비전 태스크에서 모든 다른 방법을 능가하는 성능을 내고, NLP 데이터셋에서 다른 방법과 대등한 성능을 낸다.
  • 더 놀라운 것: temperature scaling은 그 일반화 버전인 vector and matrix Platt scaling을 능가한다.
  • Matrix scaling은 잘 동작하지 않았고, Binning Method는 calibration을 올려주지만 temperature scaling만큼은 아니다.

Reliability diagrams

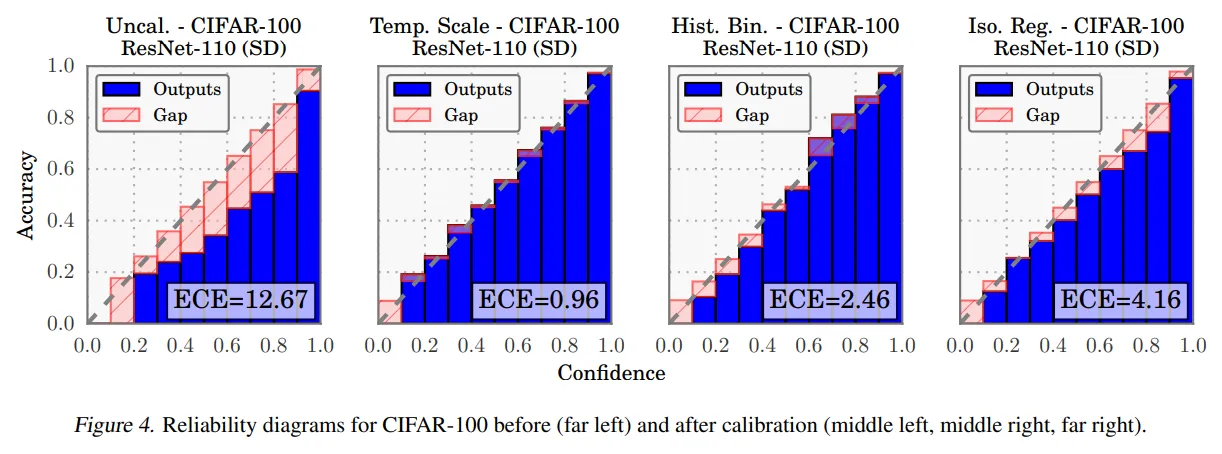
• Figure 4는 CIFAR-100를 학습한 110-layer ResNet의 calibration 전후 reliability diagram을 나타낸 것이다.
  • uncalibrated ResNet은 overconfident한 경향이 있다.
  • temperature scaling 이후의 효과를 눈으로 확인할 수 있다.
  • 여러 방법 중에서도 temperature scaling이 가장 항등함수에 가까운 결과를 낸다.

Computation time

• 소개한 모든 방법은 validation set의 샘플 수에 선형적으로 증가한다.
• Temperature scaling은 가장 빠른 방법인데, 1차원 convex optimisation problem이기 때문이다.
  • Conjugate gradient solver를 쓰면 최적의 temperature를 10번의 iteration만에 찾을 수 있다.

Ease of implementation

• Temperature scaling은 단순히 nn.MulConstant 을 logit과 softmax 사이에 끼워넣기만 하면 되며, 그 파라미터는 $1/T$이다.
  • 처음엔 이 값을 1로 설정하되, validation set을 통해 optimal value를 찾아나갈 수 있다.

6. Conclusion

• 현대의 딥러닝 모델은 이상한 현상을 보인다
  • 확률적 오류와 miscalibration
  • 근데 그와중에 오류율은 낮고…
• 최근 신경망 구조와 학습과 구조의 발전이 신경망의 calibration에 큰 영향을 줬다.
  • model capacity, normalisation, regularisation 등
  • 그것이 “왜” 정확도는 높이면서 calibration에 악영향을 미치는지는 후속 연구로서 남는다.
• 그래도 간단한 방법만으로 이러한 miscalibration을 보완할 수 있다.
  • Temperature scaling은 간단하고, 빠르고, 가장 직관적이다.
  • 그렇게 간단한 것이 자주 가장 효율적이다.