피보나치 제너레이터를 자바스크립트로 작성하며 깨달은 놀라운 점 7가지

• 이 글은 7 Surprising Things I Learned Writing a Fibonacci Generator in JavaScript를 번역한 글입니다.
• 아직 입문자이다보니 오역을 한 경우가 있을 수 있습니다. 양해 부탁드립니다.
• 매끄러운 문맥을 위하여 의역을 한 경우가 있습니다. 원문의 뜻을 최대한 해치지 않도록 노력했으니 안심하셔도 됩니다.
• 영어 단어가 자연스러운 경우 원문 그대로의 영단어를 적었습니다.
• 저의 보충 설명은 인용문에 달았습니다.

ES6에서 새로 등장한 Generator와 Iterator가 빈번하게 등장합니다. 이 글에서는 각각을 제너레이터와 이터레이터로 부르겠습니다.

제너레이터 함수는 ES6에서 소개된 자바스크립트의 새로운 기능입니다. 보다 깊게 알아보기 위하여, 피보나치 제너레이터 함수를 만들어보기로 하였습니다.

그 과정에서 배운 것들을 여기에 적어봅니다.

새로운 기능 받아들이기

새로운 언어 기능이 도입되면, 그 기능들은 모두 익히고 바로 실무에 적용하는 편입니다. 이번에 ES6에 새로 들어온 몇몇들도 마찬가지입니다. 이 중에 가장 마음에 드는 것들을 골라서 명단을 만들고 ROAD MAP이라고 이름지어봤습니다:

• R: Rest & Spread
• O: Object Literal Shortcuts (객체 관련된 축약 문법들)
• A: Arrow Function
• D: Destructing & Default Parameters
• M: Modules
• A: Asynchronous P: Programming (프라미스와 제네레이터)

막 명단을 만들었을 때, 이 명단의 것들이 앞으로 가장 자주 쓰게 될 ES6 기능일 것이라고 생각했습니다. 처음에는 제너레이터에 대한 것이 굉장히 마음에 들었지만, 조금 사용해보고 나니, 실제 제 어플리케이션 코드 상에서 제너레이터를 잘 활용한 사용례(use-case)를 찾기 힘들었습니다. 제너레이터가 필요한 대부분의 경우라면 저는 오히려 RxJS를 사용했습니다. API가 훨씬 풍부하기 때문이죠.

그렇다고 제너레이터에 대한 좋은 예시가 없다는 의미는 아닙니다. 제너레이터 때문에 제가 미쳐버리기 전에 자바스크립트 엔진이 보다 향상되기를 기다린 것이라고 변명해보지만, 그저 제가 제너레이터의 관점에서 생각하지 않았던 것일 수 있죠. 가장 좋은 해결책은 연습, 또 연습입니다.

현재 자바스크립트 문법에 제너레이터가 추가되었지만, 그다지 사용하기 편리하지 않다는 점을 지적하고있는 듯 하군요.

제너레이터를 보고 가장 먼저 생각난 사용 예시는, 무한 수열에서 값을 취하는 경우입니다. 다양한 어플리케이션이 있겠죠, 예를 들면 그래픽 작업, 컴퓨터 게임의 레벨 제너레이터, 음악 시퀀스 등...

피보나치 수열이란 무엇인가?

피보나치 수열은 여러분 모두가 알 만한 간단하고 전형적인 예시입니다. 기본적인 내용을 소개해드리죠.

피포나치 수열은 숫자의 연쇄입니다.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

첫 시드값인 0과 1 이후에는 각 누적값은 이전의 두 숫자의 합입니다. 이 수열의 흥미로운 특징은 바로 이전 값과 현재 값 간의 비율이 황금 비율인 1.61803398875... 로 수렴한다는 것이죠.

피보나치 수열을 사용하면 자연 현상에서 발생하는 황금 나선과 같은 흥미로운 것들을 만들어낼 수 있습니다.

제너레이터 함수는 무엇인가?

제네레이터 함수는 ES6에 추가된 새로운 기능으로, 이 함수는 시간이 흘러감에 따라 다양한 값들을 생성합니다. 제네레이터 함수는 객체를 반환하는데, 이 객체는 제네레이터 함수로부터 한번에 하나씩 값을 가져오도록 반복하여 사용될 수 있습니다.

제너레이터 함수가 호출되면, 값이 바로 반환되는 것이 아니라 이터레이터 객체가 반환됩니다.

이터레이터 프로토콜

이터레이터 객체는 .next() 메서드를 가집니다. .next() 메서드가 호출되면, 제너레이터 함수 내에서는 바로 직전에 .next()가 호출된 뒤 실행되고 있었던 지점의 바로 다음 줄부터 함수가 다시 명령을 수행하기 시작합니다. 그렇게 계속 명령을 수행하다가, yield를 만나고 나면 다음과 같이 생긴 객체를 반환하고 멈춥니다:

{
  value: Any,
  done: Boolean
}

value 속성은 산출값(yielded value)을 포함하며, done은 제너레이터 함수가 가장 마지막 값을 산출해냈는지 여부를 나타냅니다.

yield 키워드는 산출로 번역하였습니다.

이터레이터 프로토콜은 자바스크립트의 다양한 경우에 있어 사용되고 있습니다. for...of 루프, 배열의 rest/spread 연산자 등에서 말이죠.

1. 제너레이터는 재귀가 싫어요

자바스크립트에서의 재귀를 떠올리면 걱정하는 버릇이 있습니다. 한 함수에서 다른 함수를 호출할 때, 새로운 함수의 상태를 저장하기 위하여 새로운 스택 프레임이 할당됩니다. 스택 프레임의 할당량은 제한되기 때문에, 무한 재귀는 메모리 문제로 이어질 수 있습니다. 그 제한량을 초과하게 되면 스택 오버플로우가 발생합니다.

스택 오버플로우는 마치 당신의 파티를 급습하여 당신의 친구들을 모조리 집으로 돌려보내는 경찰들과도 같은 존재입니다. 정말 성가신 존재들이죠.

ES6에서 꼬리 호출(Tail Call) 최적화가 도입되었다는 소식에 저는 굉장히 기뻤습니다. 이제 재귀 함수는 매 반복마다 같은 스택 프레임을 재사용할 수 있게 되었습니다 - 단, 재귀 호출이 꼬리 위치 에서 이루어졌을 때에만 가능합니다. 꼬리 위치에서의 호출이란, 함수가 더 이상의 추가적인 계산 없이 재귀 호출의 결과를 반환하는 것입니다.

• 통상적인 경우라면 스택 프레임이 중첩되어 쌓여나가게 되겠죠. 그러면 결과의 반환은 불변 규칙(Invariant) 검사에 따라 더 이상 재귀가 진행되지 못할 때까지는 발생하지 않을 것입니다. 그렇게 되면 가장 최상단의 스택 프레임부터 순차적으로 결과를 반환하게 되고, 맨 아래의 스택 프레임에서는 재귀 함수의 최종 결과물을 받아볼 수 있게 되겠죠.
• 그렇지만 꼬리 호출이 이루어지면, 호출을 이어나가기에 앞서 현재 스택 프레임에서 얻은 계산 결과를 바로 이전의 스택 프레임으로 우선 반환하게 됩니다. 그러면 작업이 끝난 스택 프레임은 해제되고, 전달받은 결과와 재귀 조건(예를 들어 이번 호출이 몇번째 호출인지) 등을 따져서 다시 다음 재귀 호출을 시도하거나 최종 결과를 반환합니다. 이렇게 되면 이상적으로는 2개의 스택 프레임으로 충분하겠죠.

좋아요! 일단 아주 순진하게 구현해보도록 합시다. 전형적인 피보나치 수열을 살짝만 바꾼 아주 명료한 형태입니다.

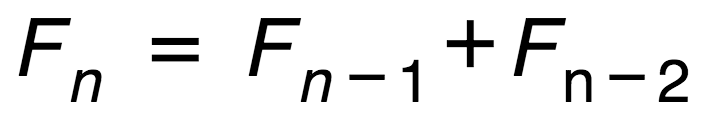
시드값 0과 1을 사용하여 수열을 시작하고, 덧셈의 결과를 함수 호출 시그니처를 통하여 넘겨 주도록 합니다. 그러면 아래와 같은 형태를 보이일 것입니다:

function* fib (n, current = 0, next = 1) {
  if (n === 0) {
    return 0;
  }

  yield current;
  yield* fib(n - 1, next, current + next);
}

코드가 깔끔하니 아주 마음에 드는군요. 함수 시그니처 상에서 시드값은 명확하게 확인할 수 있고, 재귀 호출 상에서도 공식을 명확하게 확인할 수 있습니다.

if 조건에서 볼 수 있듯, n의 값이 0이 되었을 때 yield를 사용하는 대신 return을 사용하여 루프를 멈출 수 있습니다. n을 (다음 함수 호출에) 전달하지 않으면, n의 값은 undefined가 되버리고 n에서 1을 빼려고 할 때 n의 값은 NaN으로 평가될 것입니다. 그렇게 되면 함수가 무한 루프에 빠져버리고 말겠죠.

이 구현은 아주 명료하고... 순진합니다. 이 함수를 큰 값으로 테스트해보니, 폭*발*해버리고 말았습니다.

(ಥ﹏ಥ)

아주 슬프게도, 꼬리 호출 최적화는 제너레이터에 적용되지 않습니다. Runtime Semantics: Evaluation의 함수 호출 명세에 따르면:
\7. tailCall을 IsInTailPosition(thisCall)로 지정한다
\8. EvaluateDirectCall(func, thisValue, Arguments, tailCall)을 반환한다

IsInTailPosition은 제너레이터에 대하여 false를 반환한다(14.6.1 참조):
\5. body가 GeneratorBody의 FunctionBody이면, false를 반환한다.

정리하자면, 무한하게 이어지는 제너레이터에 대하여서는 재귀를 피하라 는 것입니다. 스택 오버플로우를 방지하려면 반복문의 형태를 사용해야만 합니다.

수정) 수 개월간 Babel을 통하여 꼬리 호출 최적화를 해오곤 했는데, 이제는 그만두게 되었습니다. 이 글을 작성하는 현재 시점(2016년 5월 15일) 기준으로 제가 알고 있는 한에서는 Webkit(Safari)만이 새로운 ES6에 적합한 꼬리 호출을 지원합니다. 엔진을 구현하는 사람들 간에 제기된 어려움 호소와 논쟁 때문에 그렇습니다.

약간 코드를 수정하여 재귀를 제거하고, 반복문을 대신 사용하도록 합니다:

function* fib (n) {
  const isInfinite = n === undefined;
  let current = 0;
  let next = 1;

  while (isInfinite || n--) {
    yield current;
    [current, next] = [next, current + next];
  }
}

위에서 볼 수 있듯, 본래의 함수 호출 시그니처에서의 것과 동일하게 변수 간의 값 교환을 수행하지만, 이번에는 while 반복문 내에서 해결할 수 있도록 구조 분해 할당을 사용하고 있습니다. 제한값을 인자로 전달하지 않았을 경우를 대비하여 제너레이터에 isInfinite가 필요합니다.

current와 next의 값이 동시에 필요한 상황이므로 구조 분해 할당을 사용하고 있습니다.

2. 매개 변수가 반복을 제한하도록 합시다

구조 분해 할당과 rest 연산자(...)를 사용하면 제너레이터로부터 배열을 추출해내는 것이 가능합니다:

const [...arr] = generator(8);

하지만 당신이 작성한 제너레이터가 무한 수열이고, 매개 변수를 통하여 한계점을 명시할 방법이 없다면, 결과로 반환되는 배열에는 멈추지 않고 계속 값이 채워질 겁니다.

┻━┻ ︵ヽ(`Д´)ﾉ︵ ┻━┻

위에서 구현한 두 피보나치 수열 모두 호출할 때에 n을 전달하도록 하므로, 이를 통하여 각 함수가 피보나치 수열의 첫 n개 값만 반환하도록 제한할 수 있죠. 아주 좋습니다!

┬─┬ ノ( ゜-゜ノ)

3. 메모이제이션이 적용된 함수를 조심히 다루세요

피보나치 수열과 같은 것을 다룰 때는, 메모이제이션(Memoization)을 적용하고 싶기 마련입니다. 그러면 반복 횟수를 획기적으로 줄일 수 있으니까요. 즉, 훨씬 속도가 빨라집니다.

메모이제이션이 무엇인가요?

동일한 인자에 대하여 동일한 결과를 반환하는 함수에 대하여, 각 결과를 따로 메모에 기록해둔 뒤 나중에 호출이 발생할 때에 활용할 수 있습니다. 그러면 해당 결과를 구하기 위하여 동일한 작업을 반복할 필요 없이, 메모를 참고하면 되겠죠. 피보나치 알고리즘은 결과를 구하기 위하여 상당량의 계산을 반복하게 되는데, 이 함수에 메모이제이션을 적용하면 시간을 상당히 절약할 수 있다는 의미입니다.

메모이제이션을 통하여 결과값을 기록해둔 것을 메모(Memo)라고 부르고 있습니다.

피보나치 제너레이터의 반복문 형태에 대하여 메모이제이션을 적용해봅시다:

const memo = [];

const fib = (n) => {
  if (memo[n] !== undefined) return memo[n];

  let current = 0;
  let next = 1;

  for (let i = 0; i < n; i++) {
    memo[i] = current;
    [current, next] = [next, current + next];
  }

  return current;
};

function* gen (n = 79) {
  fib(n);
  yield* memo.slice(0, n + 1);
}

n의 값이 피보나치 값의 배열에 대한 인덱스로서의 역할을 충분히 해내기 때문에, 이를 그대로 배열의 인덱스로 활용할 수 있습니다. 뒤이어 발생하는 호출은 단지 이 인덱스를 참조하여 이에 대응하는 결과값을 반환합니다.

수정) 이 코드의 원본은 버그가 있습니다. 이 함수는 처음에 실행하면 정상 작동하겠지만, 알맞은 메모를 찾았을 때에 값을 산출해낼 수 없으므로 메모가 정상적으로 기록되지 않습니다. return과 달리, yield는 함수의 나머지 부분이 실행을 멈추게 하지 않습니다. 단지 .next()가 호출되기 전까지 실행을 일시정지시킬 뿐입니다.

위에 제시된 코드는 수정된 버전이어서 원본 코드가 무엇이었는지 알 길이 없습니다. 원본 코드도 올려주었으면 비교할 수도 있고 좋았을텐데 아쉽습니다.

이 부분이 제 머릿속을 정리하는 데에 있어서 가장 어려운 부분이었습니다. 제너레이터에서 yield는 return과 다릅니다. next()를 사용하여 함수를 재개하는 것이 로직을 작성하는 방향에 어떻게 영향을 미칠지에 대해서도 곰곰이 따져봐야 합니다.

이번 경우에는 yield를 사용한 로직이 제대로 작동하도록 하는 데에는 성공했지만, 제어 흐름을 파악하기 어려워졌습니다.

위와 같은 방식으로 메모이제이션을 적용할 수 있는 경우, 계산 관련 로직과 제너레이터 함수를 서로 분리시키는 것이 훨씬 가독성을 향상시킨다는 결론을 내렸습니다.

위에서 볼 수 있듯, 새로 작성한 제너레이터 함수는 굉장히 간단합니다. 메모이제이션을 적용한 fib()를 호출하여 메모를 계산하고, yield*를 사용하여 계산 결과를 담고 있는 반복 가능한 배열에 제너레이터를 위임합니다.

Iterable은 반복 가능(한 것)으로, Delegate는 위임으로 번역했습니다.

yield*는 yield의 특수한 형태로, 다른 제너레이터 또는 반복 가능한 객체로 위임합니다. 다음 예시를 참고해주세요:

const a = [1, 2, 3];
const b = [4, 5, 6];

function* c () {
  yield 7;
  yield 8;
  yield 9;
}

function* gen () {
  yield* a;
  yield* b;
  yield* c();
  yield 10;
}

const [...sequence] = gen();
console.log(sequence); // [1,2,3,4,5,6,7,8,9,10]

yield* 문서와 Iterator Protocol를 참고하시면 더 자세한 내용을 확인할 수 있습니다.

Benchmarks

동일 작업을 위한 서로 다른 알고리즘을 비교할 때면 간단한 벤치마크 스크립트를 작성하여 성능을 비교하곤 합니다.

이번 테스트를 위하여 79개의 값을 처리하도록 했습니다. Node의 process.hrtime()을 사용하여 나노초 단위로 시점을 체크하였고, 총 3회의 테스트를 돌려서 결과를 평균냈습니다:

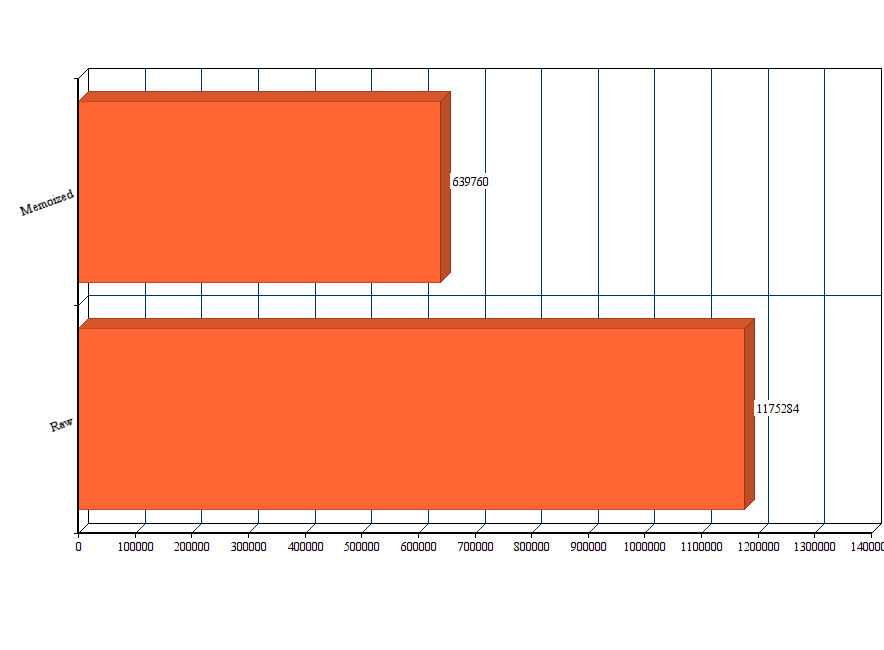
위에서 볼 수 있듯 상당한 차이가 발생합니다. 크기가 큰 수를 빠르게 처리해야 한다면, 메모이제이션은 아주 현명한 해법임이 확실합니다.

단 한 가지 문제가 있군요. 무한 수열의 경우, 메모 배열은 끝도 없이 커질 것입니다. 결국에는 힙 크기 제한에 걸려서 자바스크립트 엔진이 뻗고 말겠죠.

하지만 걱정할 것 없습니다. (??) 자바스크립트의 정수가 가질 수 있는 크기의 최대값은 9007199254740991입니다. 이 값은 1000조를 육박하는 커다란 수치입니다만, 피보나치 수열의 경우 이것으로 만족하지 못하죠. 피보나치 수열은 아주 빠르게 값이 커집니다. 79번째만 되더라도 이 최대값을 넘기고 말 겁니다.

왜 걱정할 것 없다고 그랬는지 저도 모르겠습니다...

4. 정밀한 타이밍을 위해선 내장 API가 필요합니다

벤치마크 스크립트를 작성할 때마다 항상 느끼는 건, Node와 브라우저 양측에서 두루 사용할 수 있는 정밀한 시간 측정 API가 있었으면 좋겠다는 것입니다. 하지만... 없죠. 이에 가장 근접한 것은, 브라우저의 performance.now() API와 Node의 process.hrtime() API를 모두 래핑해주는 통합된 API일 겁니다. 하지만 현실적으로는 Node를 사용하는 벤치마크로도 이번 테스트에는 충분할 겁니다.

유일한 불만은 Node의 process.hrtime()이 단일값 대신 배열로 결과를 반환한다는 것입니다. 물론, 이것은 쉽게 고칠 수 있습니다:

const nsTime = (hrtime) => hrtime[0] * 1e9 + hrtime[1];

이 함수에 process.hrtime()의 결과 배열을 전달하는 것으로 친숙한 나노초 결과를 돌려받을 수 있을 것입니다. 메모이제이션 버전과 반복 버전을 비교하기 위하여 작성한 벤치마크 스크립트를 살표보도록 합시다:

import iterativefib from 'iterativefib';
import memofib from 'memofib';
import range from 'test/helpers/range';

const nsTime = (hrtime) => hrtime[0] * 1e9 + hrtime[1];

const profile = () => {
  const numbers = 79;
  const msg = `Profile with ${ numbers } numbers`;

  const fibGen = iterativefib();
  const fibStart = process.hrtime();
  range(1, numbers).map(() => fibGen.next().value);
  const fibDiff = process.hrtime(fibStart);

  const memoGen = memofib();
  const memoStart = process.hrtime();
  range(1, numbers).map(() => memoGen.next().value);
  const memoDiff = process.hrtime(memoStart);

  const original = nsTime(fibDiff);
  const memoized = nsTime(memoDiff);

  console.log(msg);
  console.log(`
    original: ${ original }ns
    memoized: ${ memoized }ns
  `);
};

profile();

hrtime()의 기능 중 제일 마음에 드는 점은 시작 시간을 함수에 인자로 전달하여 소요 시간을 얻어낼 수 있다는 것입니다. 프로파일링을 할 때에 필요한 바로 그것이죠.

때로는 프로세스가 OS 작업 스케줄러에 의하여 지연되는 운이 나쁜 경우도 있기 때문에, 스크립트를 여러번 돌려서 평균 결과를 얻도록 했습니다.

여러분의 코드를 벤치마킹할 수 있는 보다 정확한 방법이 있을 것이라고 확신하지만, 어쨌든 위의 코드 정도면 대부분의 경우에 충분하게 활용할 수 있습니다. 특히 이번과 같이 확실한 승자 - 메모이제이션이 적용된 피보나치 구현과 같은 경우 말이죠.

5. 부동소수점 정밀도 오류를 조심하세요

일단, 지루하고 어려운 수학 이야기를 하려는 게 아니니 오해하지 마세요. 혹시 반복이나 재귀 없이도 피보나치 수열을 효율적으로 계산할 수 있는 방법이 있다는 것을 아시나요? 아래와 같이 생겼습니다.

const sqrt = Math.sqrt;
const pow = Math.pow;

const fibCalc = n => Math.round(
  (1 / sqrt(5)) *
  (
    pow(((1 + sqrt(5)) / 2), n) -
    pow(((1 - sqrt(5)) / 2), n)
  )
);

유일한 문제점은 부동소수점 정확도의 한계입니다. 실제 공식에서는 내림이 사용되지 않습니다. 여기에 사용한 이유는 부동소수점 오류가 n이 11보다 커지고나면 결과값이 조금씩 어긋나게 만들기 때문입니다. 그다지 좋지 않죠.

다행인 소식은, 내림을 사용하면 정확도를 n이 75일 때까지 보장할 수 있다는 것입니다. 훨씬 좋군요. 자바스크립트의 Number 자료형을 사용했을 때 최대로 정확한 정수값인 79를 조금 밑도는 값이니까요.

따라서 n이 75보다 큰 경우가 아니라면, 이 빨라진 공식은 정상적으로 작동합니다! 제너레이터 패턴으로 바꿔보도록 합시다.

const sqrt = Math.sqrt;
const pow = Math.pow;

const fibCalc = n => Math.round(
  (1 / sqrt(5)) *
  (
    pow(((1 + sqrt(5)) / 2), n) -
    pow(((1 - sqrt(5)) / 2), n)
  )
);

function* fib (n) {
  const isInfinite = n === undefined;
  let current = 0;

  while (isInfinite || n--) {
    yield fibCalc(current);
    current++;
  }
}

좋아보입니다. 벤치마크를 돌려보도록 하죠:

79번째 값으로 프로파일링
     original: 901643ns
     memoized: 544423ns
     formula: 311068ns

훨씬 빨라졌죠? 하지만 일부 자릿값이 없어졌습니다. 적당한 트레이드-오프로군요.

¯\(º_o)/¯

6. 제약 사항

미리 일러둘 점이 몇가지 있습니다:

• 자바스크립트 표준 Number 자료형만을 사용한다면, 이 수열에 대하여 정확한 값을 어디까지 얻어낼 수 있는지 알 수 없습니다.
• formula 버전(바로 위의 fibCalc를 사용한 코드)를 사용한다면, 이 수열에 대하여 정확한 값을 어디까지 얻어낼 수 있는지 알 수 없습니다.
• 정확한 값을 얻기 위하여 재귀 호출을 얼마나 해야 하는지 알 수 없습니다.

하지만 위의 제약 사항을 알고 있는 지금이라면, 여태껏 보여드리지는 않았습니다만 최고의 피보나치 수열 구현은 이것입니다:

const lookup = [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,
987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393,
196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465,
14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296,
433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976,
7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272,
139583862445, 225851433717, 365435296162, 591286729879, 956722026041,
1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723,
17167680177565, 27777890035288, 44945570212853, 72723460248141,
117669030460994, 190392490709135, 308061521170129, 498454011879264,
806515533049393, 1304969544928657, 2111485077978050, 3416454622906707,
5527939700884757, 8944394323791464];

function* fib (n = 79) {
  if (n > 79) throw new Error('Values are not available for n > 79.');
  yield* lookup.slice(0, n);
}

실제 어플리케이션에서 무한 수열을 사용한 대부분의 경우, 특정 목적을 위하여 제한된 수량의 값만이 필요할 뿐이었습니다(보통 그래픽 작업). 별도의 Lookup 테이블에서 값을 가져오는 편이 직접 값을 계산하는 것보다 훨씬 빠른 경우가 많았습니다. 사실 이것은 8-90년대 컴퓨터 게임에서 흔하게 사용된 최적화 방식이기도 합니다. 아마 지금도 그럴 겁니다.

ES6에서는 배열이 반복 가능한 객체이고, 기본적으로 제너레이터와 동일하게 동작하므로, yield*를 사용하여 Lookup 테이블에 손쉽게 위임할 수 있습니다.

전혀 놀라울 것도 없이, 이것이 가장 빠른 구현입니다:

79번째 값으로 프로파일링
original: 901643ns
memoized: 544423ns
formula: 311068ns
lookup: 191683ns

돌이켜 보면, 정확한 값을 사용하는 것으로만 문제를 한정지었다면 호출 스택은 전혀 걱정이 안 되었으리라 생각합니다... 살짝 수정한 재귀 버전이면 아마도 괜찮을 겁니다:

const memo = [0, 1];

const fib = (n) =>
  memo[n] !== undefined ? memo[n] :
  memo[n] = fib(n - 1) + fib(n - 2);

function* gen (n = 79) {
  if (n > 79) throw new Error('Accurate values are not available for n > 79.');
  fib(n);
  yield* memo.slice(0, n);
}

export default gen;

제가 가장 좋아하는 대목이 여기입니다. 시드값이 메모에 기록되면서 실제 계산 결과는 수학적 재귀 관계 Fn = Fn-1 + Fn-2 에 가장 근접하게 됩니다.

제너레이터는 단순히 메모 배열에 또 위임하기만 하면 됩니다.

주의해야 할 제한 사항

• 부동소수점이 필요한 공식을 사용한다면, 정밀도의 한계를 확실하게 검사해야 합니다.
• 기하급수적으로 증가하는 수열을 사용한다면, 자바스크립트의 Number 자료형의 한계에 도달하기 전 어디까지 수열을 사용할 수 있는지 파악해두어야 합니다.
• 한계값이 작은 편이라면, 배포용 앱의 속도 향상을 위하여 룩업 테이블을 미리 만들어서 사용하는 것을 고려해보세요.
• 자바스크립트가 네이티브로 지원하는 것보다 더 큰 정밀도의 숫자를 사용해야 한다면, 아예 불가능한 것은 아닙니다. BigInteger와 같이 큰 수를 다루는 정수 라이브러리를 사용할 수 있습니다.

제너레이터와 유사하게 작동하는 것들이 많이 있습니다

ES6에서 제너레이터 함수가 처음 소개되었을 때, 많은 내장 객체들이 이터레이터 프로토콜을 구현했습니다 (여기서 이터레이터 프로토콜이란 계속 반복해서 사용할 수 있는 객체를 제너레이터가 반환하는 방식을 말합니다).

더 정확하게 말하면, 반복 가능 프로토콜(Iterable Protocol)을 구현했습니다. String, Array, TypedArray, Map, 그리고 Set은 모두 내장된 반복 가능한 객체입니다. 즉, 앞서 언급한 객체들은 열거할 수 없는 [Symbol.iterator] 속성을 가집니다.

다르게 말하면, 내장된 유사 배열 객체에 대하여 이터레이터의 .next() 메서드를 통하여 반복 사용할 수 있습니다.

이제 배열 이터레이터에 어떻게 접근할 수 있는지 다뤄보도록 하겠습니다. 반복 가능 프로토콜을 구현하는 것과 동일한 기법을 사용하면 됩니다.

let arr = [1,2,3];
let foo = arr[Symbol.iterator]();

arr.forEach(() => console.log( foo.next() ));
console.log(foo.next());
// { value: 1, done: false }
// { value: 2, done: false }
// { value: 3, done: false }
// { value: undefined, done: true }

여러분이 원한다면 고유한 반복 가능 객체를 만들 수도 있습니다.

const countToThree = {
  a: 1,
  b: 2,
  c: 3
};

countToThree[Symbol.iterator] = function* () {
  const keys = Object.keys(this);
  const length = keys.length;

  for (const key in this) {
    yield this[key];
  }
};

let [...three] = countToThree;
console.log(three); // [ 1, 2, 3 ]

기존의 내장된 반복 가능 객체의 동작을 다시 정의할 수도 있지만, 조심해야 합니다. V8 엔진과 Babel 간에 일관성 없는 동작이 발견되고 있습니다.

const abc = [1,2,3];

abc[Symbol.iterator] = function* () {
  yield 'a';
  yield 'b';
  yield 'c';
};

let [...output] = abc;
console.log(output);
abc.forEach(c => console.log(c));

// babel logs:
/*
[1,2,3]
1
2
3
*/

// Node logs:
/*
[ 'a', 'b', 'c' ]
1
2
3
*/

arr[Symbol.iterator]()를 쉽게 실행할 수 있는 단축키 같은 함수를 만들면 편리하겠다는 생각을 해서, 그러한 API를 만들어서 여러분께 제공해드리니 배열을 간단하게 이터레이터로 변화하는 데에 활용하시길 바랍니다. 저는 이것을 arraygen 이라고 부르기로 했습니다. Github에서 확인하실 수 있습니다.

결론

부디 이 글을 통하여 여러분들이 제너레이터에 대하여 몰랐던 점들을 알아가실 수 있기를 바랍니다. 몇몇 흥미로운 다른 이야기를 하느라 옆길로 새기도 했군요.

1. 재귀를 피하세요. 제너레이터는 최적화된 꼬리 호출을 수행할 수 없습니다.
2. 매개 변수를 사용하여 제너레이터의 길이를 제한하세요. 매개 변수를 해체 할당할 때 ...(rest) 연산자를 사용할 수 있습니다.
3. 무한대를 다루는 제너레이터를 메모이징하면 힙 사이즈 제한 문제를 해결할 수 있습니다.
4. 자바스크립트에는 정밀한 시점 계산에 사용되는 2가지 좋은 API를 제공합니다. 왜 같이 사용할 수 없는 걸까요? (ಥ﹏ಥ)
5. 부동소수점 정밀도 오차로 인하여 공식 기반의 무한대 제너레이터가 오작동할 수 있으니 조심하세요.
6. 제한 사항을 분명히 파악하세요. 당신의 앱이 요구하는 계산 한도를 제너레이터가 충족시킬 수 있나요? 그 계산 한도를 충족시킬 수 있는 정밀도를 지원하나요? 사용할 자료형의 한계치를 초과할 수도 있나요? 자바스크립트 엔진이 제너레이터의 동작을 감당할 수 있을 만큼의 메모리를 확보할 수 있나요?
7. 대부분의 내장 객체는 반복 가능 프로토콜을 활용하여 제너레이터와 유사하게 동작할 수 있습니다. 또한 여러분이 고유한 반복 가능 객체를 정의할 수도 있습니다.

이 글에서 사용된 피보나치 예제를 실제로 사용해보고 싶다면, 전체 소스를 Github에서 클론할 수 있습니다.