DFS 찍먹 ( BOJ11724 - Java )

DFS?

완전탐색의 방법중 하나. 그래프 탐색 방법!

그래프안에서 노드의 최하점까지 쭉 들어가는 탐색!

인접 리스트로 구현 시 O(N+E)이다. (N == node, E == edge)

보통 재귀함수나, 스택을 사용해서 표현된다. 사실상 둘이 같음

• 재귀함수 dfs가 호출되고, 값이 처리되는 과정을 보면 (숫자는 호출순서)
  dfs(1) -> dfs(2) -> dfs(3) -> ... -> dfs(N) ::: 호출순서
  dfs(N) -> dfs(N-1) -> ... dfs(1) ::: 값이 처리되는 순서
  Stack처럼, FILO(First in last out)이다. 맨 첨 호출한놈이 맨 마지막에 나옴!

---

문제 링크 - BOJ11724

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class BOJ11724{
        static boolean[] visited;
        static ArrayList<Integer>[] A;
        public static void main(String[] args) throws IOException {
            BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

            StringTokenizer st = new StringTokenizer(br.readLine());

            int n = Integer.parseInt(st.nextToken()); // 노드 개수
            int m = Integer.parseInt(st.nextToken()); // 엣지 개수

            visited = new boolean[n + 1]; // 0번 인덱스 사용하면 헷갈리니까 걍 N+1 선언

            A = new ArrayList[n+1];

            for (int i = 1; i < A.length; i++) {
                A[i] = new ArrayList<>(); // 실제 객체 선언
            }
            for (int i = 0; i < m; i++) { // 엣지 개수만큼 (== 주어지는 엣지 정보 담기 위해)
                st = new StringTokenizer(br.readLine());
                int start = Integer.parseInt(st.nextToken());
                int end = Integer.parseInt(st.nextToken());

                A[start].add(end); //  시작점에서 종료점으로 갈 수 있다
                A[end].add(start); // 종료점에서 시작점으로 갈 수 있다.
            }

            int count = 0;

            for (int i = 1; i < n + 1; i++) { // 1~n+1 이 어레이리스트의 유효지점이기 때문에 맞춰준다
                if (!visited[i]){ // 방문하지 않은 노드가 있으면
                    count++;
                    dfs(i); // 방문하지 않은 해당 노드 기준으로 dfs 실행!
                }
            }
            System.out.println(count);
        }

        private static void dfs(int node) {
            if (visited[node]){ // 현재 노드가 이미 방문한 노드라면
                return;
            }
            visited[node] = true; // 방문하지 않았으면, 방문으로 만들고
            for (Integer integer : A[node]) { // 현재 노드에서 연결되어 있는 노드 모두 돌면서
                if (!visited[integer]){ // 인접리스트 안에 있는 요소가 아직 탐색되지 않은 노드라면
                    dfs(integer); // 탐색하지 않은 노드 기준으로 다시 dfs 실행해라!
                }
            }
        }
    }

• ArrayList활용한 인접 리스트 만들기가 중요하다.
• 이 인접 리스트는 각 노드마다의 "연결 정보"를 저장한다.

				...
                A[start].add(end); //  시작점에서 종료점으로 갈 수 있다
                A[end].add(start); // 종료점에서 시작점으로 갈 수 있다.
                ...

• 이 부분처럼, 특별히 방향이 설정되어 있는 엣지가 아니라면 양방향 모두 추가해줘야 한다.

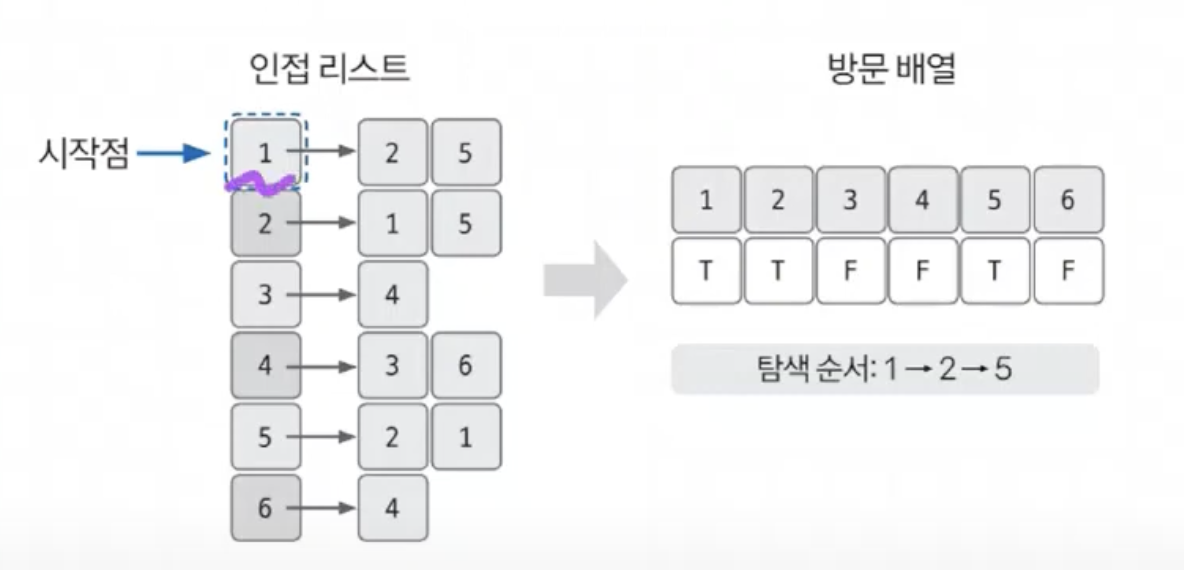
위와 같은 형태가 됨 (이미지 출처)

• 더해서 boolean[] visited 배열 사용해서 방문한 노드는 체크한다.

---

난 이게 왤캐 어렵지? 문제를 좀 더 많이 풀어서 생소함을 깨쳐야겠다.
아마도 생소함 때문일듯! "인접 리스트" 아이디어가 내게 없었다. 강의를 듣는 이유를 알겠군