프로그래머스 누적합 - 연속 펄스 부분 수열

문제 링크

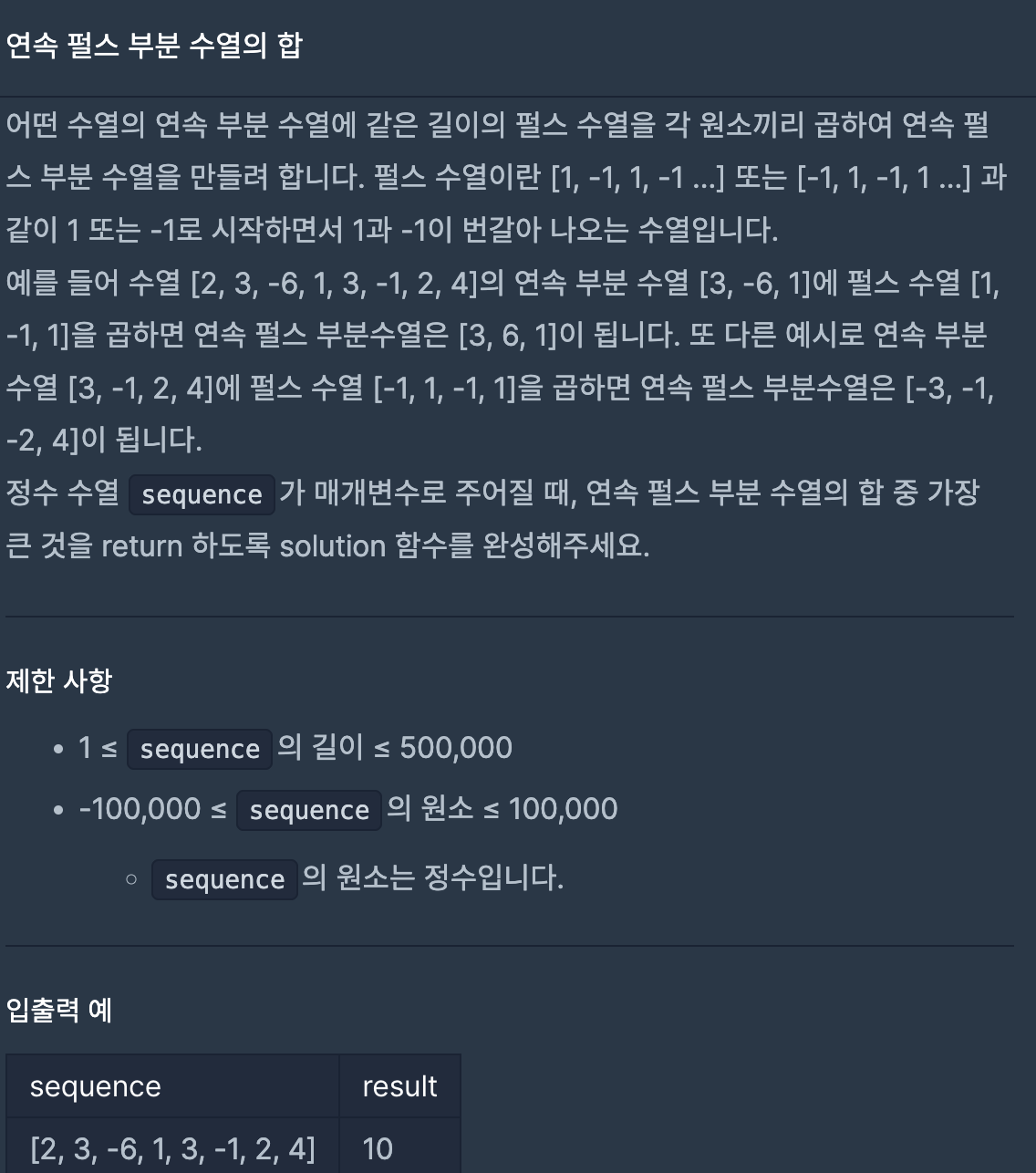
• 최대 구간합을 구한다?
• 입력 범위가 매우 크다?(즉, 완탐같은걸로 풀면 안된다?)

그럼 넌 누적합이야

풀이

    public long solution(int[] sequence) {
        // 요구사항 - 어쨌든 시퀀스안에서 누적합이 제일 큰 녀석 - 젤 작은 녀석
        // 그러면, pulse 1, pulse2 해서 누적합 배열을 두 개 만들어?
        
        // 예시의 누적합 구해보자
        // 2, {3, -6,1,} 3,-1, 2, 4

        // 2, -1, -7, -8, -5, -4, -2, -6  {1,-1...}

        // -2, 1,  7,  8,  5,  4,  2,  6 {-1,1,1} 양음만 반대다. 그럼 하나로 되겠는데?
        
        // 젤 큰놈 - 작은놈 = 10 (누적합의 차가 젤 큰놈이 구간합 최대니까)

        long[] prefixSum = new long[sequence.length + 1];

        for (int i = 1; i < prefixSum.length; i++) {
            if (i % 2 == 0){
                prefixSum[i] = prefixSum[i - 1] + sequence[i - 1] * -1;
            } else {
                prefixSum[i] = prefixSum[i - 1] + sequence[i - 1];
            }
        }

        long max = Long.MIN_VALUE;
        long min = Long.MAX_VALUE;

        for (int i = 0; i < prefixSum.length; i++) {
            if (prefixSum[i] > max){
                max = prefixSum[i];
            }
            if (prefixSum[i] < min){
                min = prefixSum[i];
            }
        }

        return max - min;
    }

• 주석으로 주저리 주저리 적어놓은 것처럼, 펄스 배열이 음수부터 시작하든 양수부터 시작하든 어차피 최대값-최소값 의 값은 같다
  why? : 2 - (-8) == 8 - (-2)
• 따라서, 누적합을 선언 할 때 짝수는 - 홀수는 +로 미리 선언
• 그 후 최대값 - 최솟값 하면 최대의 구간합을 찾을 수 있다.

---

다른 사람의 풀이(멋짐)

출처 블로그

class Solution {
    public long solution(int[] sequence) {
        int a = 1,
        b = -1,
        size = sequence.length;
        
        long aSum = sequence[0],
        bSum = sequence[0] * -1,
        aMin = 0,
        bMin = 0,
        max = Long.MIN_VALUE;
        
        for (int i = 1; i <= size; i++) {
            a *= -1;
            b *= -1;
            
            max = Math.max(max, aSum - aMin);
            max = Math.max(max, bSum - bMin);
            
            aMin = Math.min(aMin, aSum);
            bMin = Math.min(bMin, bSum);
            
            if (i == size) break;
            
            aSum += sequence[i] * a;
            bSum += sequence[i] * b;
        }
        
        return max;
    }
}

• 선언과 비교를 동시에! 어케 생각한거지?...

---

정리

이전 포스트에서 렝스+1 로 구간합 선언이 싫다고 했는데, 아주 후회한다. 계산이 오히려 너무 복잡하고 어지러워져서 렝스+1이 훨씬 편한듯.