DP(Dynamic Programming)이란

컨셉은 다음과 같다.

• 문제를 부분 문제로 분할한다
• 부분 문제의 해를 기억 한다. (혹은 저장한다)
• 기억한 해를 이용해서 전체 문제를 푼다.

제일 중요한 컨셉은 기억이다.

DP 사용 이유

같은 작업을 중복적으로 수행하는 경우를 피하고, 이전에 계산한 값을 저장해 재활용하여 계산 속도를 높이기 위함이다.

DP 단골 문제인 피보나치 수열은 다음과 같은 계산 과정이 들어간다.

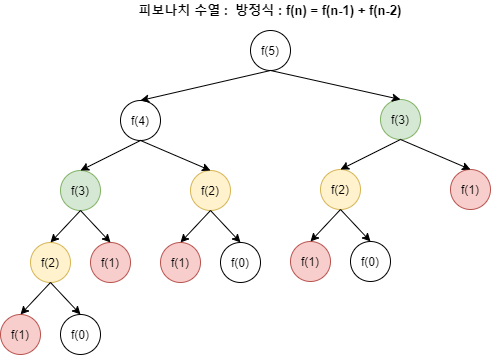
출처(이미지)

public int fibonacci(int n) {
        if(n <= 1) {
            return n;
        }
        return fibonacci(n-1) + fibonacci(n-2);
    }

위 fibonacci 매서드는 재귀적으로 fibonacci 매서드를 호출한다. 따라서

f4 = f3, f2

f5 = f4,f3,f2

f6 = f5,f4 ...

위와 같이 수많은 중복 계산이 들어가게 된다.

이를 방지하기 위해서 값을 기억/저장 해놓고, 재사용한다는 아이디어가 DP의 핵심이다

---

Tabulation

예시 코드

public int fibonacciTabulation(int n) {
    int[] dp = new int[n+1];
    dp[0] = 0;
    dp[1] = 1;
    
    for(int i=2; i<=n; i++) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    
    return dp[n];
}

위 함수는 반복문을 통해서 피보나치 수열을 구하고, 배열에 값을 "저장"해나가면서 피보나치 수열을 완성시켜 [n]번째 피보나치 수열의 값을 구한다.

위 코드 예시처럼 Tabulation 이란 Bottom-up 방식으로, 반복문과 배열 등을 사용해서 값을 계속해서 저장해나가고, 이 저장한 값을 재사용한다.

Memoization

public int fibonacciMemoization(int n) {
    int[] memo = new int[n+1];
    Arrays.fill(memo, -1);
    return fibonacciMemoizationHelper(n, memo);
}

private int fibonacciMemoizationHelper(int n, int[] memo) {
    if(n <= 1) {
        return n;
    }
    if(memo[n] != -1) {
        return memo[n];
    }
    memo[n] = fibonacciMemoizationHelper(n-1, memo) + fibonacciMemoizationHelper(n-2, memo);
    return memo[n];
}

위와 같은 코드 형태로 이루어진다.

public int fibonacciMemoization(int n) {
    int[] memo = new int[n+1];
    Arrays.fill(memo, -1);
    return fibonacciMemoizationHelper(n, memo);
}

• 이 부분에서 메모 배열을 생성, 초기화한다.
• 배열의 크기는 n+1이며, 이는 n이 인덱스로써 활용되어 재귀되기 때문이다
• 배열을 -1로 초기화 하는 부분이 중요하다.

• Memoization은 이전에 계산한 값을 저장해두고, 다음 번에 동일한 계산이 필요할 때 이전에 저장된 값을 사용하여 중복 계산을 피하는 방법이다.

• 이를 위해서 계산한 값과 계산하지 않은 값의 구분이 필요하다.
• 따라서 초기값을 중복되지 않을 값인 -1 로 초기화해서 Memoization 을 수행한다.

private int fibonacciMemoizationHelper(int n, int[] memo) {
    if(n <= 1) {
        return n;
    }
    if(memo[n] != -1) {
        return memo[n];
    }
    memo[n] = fibonacciMemoizationHelper(n-1, memo) + fibonacciMemoizationHelper(n-2, memo);
    return memo[n];
}

위에서는 재귀를 통해 피보나치 수열을 선언하고, 구해간다.