N개의 최소공배수 (프로그래머스) 자바 (With 유클리드 호제법)

개요

문제 링크

재밌는 문제인듯! 유클리드 호제법 기억이 안나서...좀 헤맸다

1. 유클리드 호제법

2개의 자연수 a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면 (단 a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.

이 성질에 따라, b를 r로 나눈 나머지 r0를 구하고, 다시 r을 r0로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.

: (출처) https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95

즉, 아래와 같은 수식으로 나타낼 수 있다. 출처

---

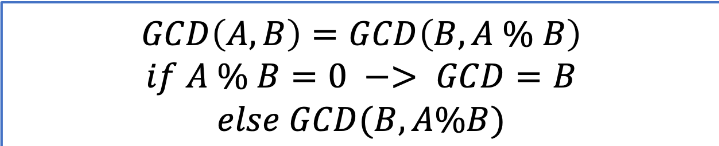
2. 자바 코드로 최대공약수(gcd), 최소공배수(lca) 구하기

자바 코드로 나타내면 다음과 같다

    
    public static int lca(int a, int b) {
        int gcd = gcd(a, b);
        return a * b / gcd;
    }

    public static int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }

유클리드 호제법에 따라 a % b == 0 이 될때까지 최대공약수를 구한다. 그리고 최소공배수 공식을 이용해서( a*b / gcd ) 최소공배수도 구해준다.

• 문제에서는 배열의 형태로 주어지므로, 0번째 인덱스와 첫번째 인덱스부터 비교하면서 최소공배수를 구해서 배열의 최소공배수를 구한다.

3. 정답 코드

class Solution {
    public int solution(int[] arr) {
        int answer = arr[0];
        for (int i = 1; i < arr.length; i++) {
            answer = lca(answer, arr[i]);
        }
        return answer;
    }
    
    public static int lca(int a, int b) {
        int gcd = gcd(a, b);
        return a * b / gcd;
    }

    public static int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }
}

---

문제에서는 "[2,6,8,14] " 와 같은 int[] 가 주어진다. 따라서 0번째-1번째 인덱스부터 쭉쭉 최소공배수를 구하면 이 배열의 최소공배수가 된다.

1st : 2 / 6 -> 6
2nd : 6 / 8 -> 24
3rd : 24 / 14 -> 168

이런 식으로 해결된다. 시간 복잡도는 O(n)