투포인터 알고리즘 (백준 2018, 1940)

문제 링크

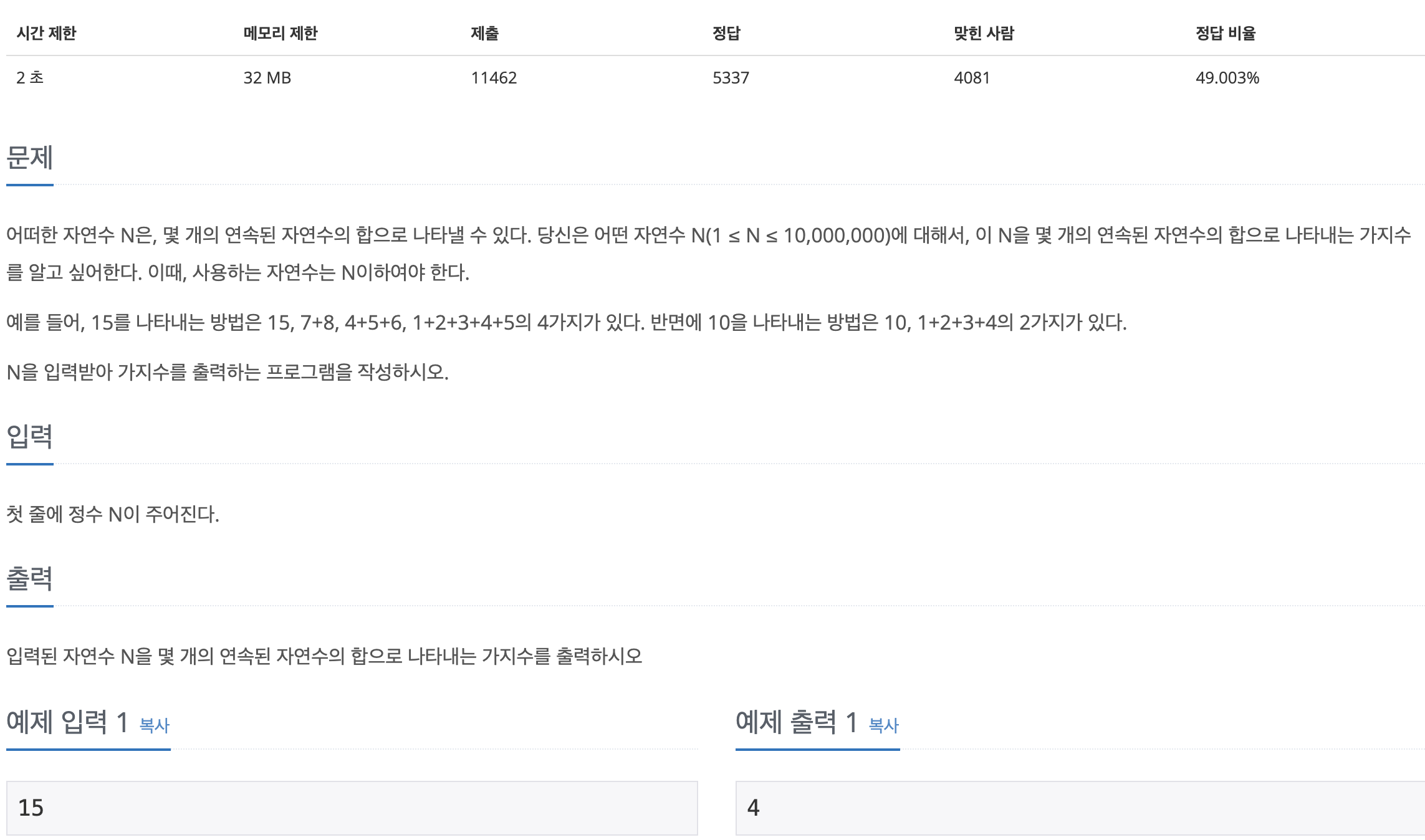
문제를 간략히 설명하면 위와 같다

"연속된" 자연수로 주어진 자연수 15를 만들기 위한 방법의 개수를 리턴하라

15를 만드는 연속된 자연수는

{1,2,3,4,5}, {4,5,6}, {7,8}, {15} 의 네가지다

주어진 N의 크기가 매~우 크고 (1000만), 따라서 O(nLogN)보다 작은 O(N)으로풀어야 함.

---

문제 풀이

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        int start = 1; // 시작 값
        int end = 1; // 끝 값
        int sum = 0; // 현재까지의 합
        int count = 0; // 경우의 수

        while (start <= N) {
            if (sum < N) {
                sum += end; // 현재까지의 합에 end 값을 더함
                end++; // end 값을 증가시킴
            } else if (sum == N) {
                count++; // 경우의 수를 증가시킴
                sum -= start; // 현재까지의 합에서 start 값을 빼고
                start++; // start 값을 증가시킴
            } else { // sum > N
                sum -= start; // 현재까지의 합에서 start 값을 빼고
                start++; // start 값을 증가시킴
            }
        }

        System.out.println(count);
    }
}

• start ~ end까지의 sum을 저장해서, 타겟 N과 비교한다
• sum < N 일 경우, 스타트에서 엔드까지의 총합이 N보다 작으므로 섬에다가 엔드를 더하고, 엔드를 하나 올려준다
• sum > N 일 경우 스타트~엔드 총합이 N을 오버했으므로 섬에서 스타트를 빼주고, 스타트를 증가시킨다
• 마지막으로 같을경우 카운트(정답)을 하나 올리고, 섬에서 스타트를 뺀 후 다시 스타트를 올려준다.

---

문제 링크

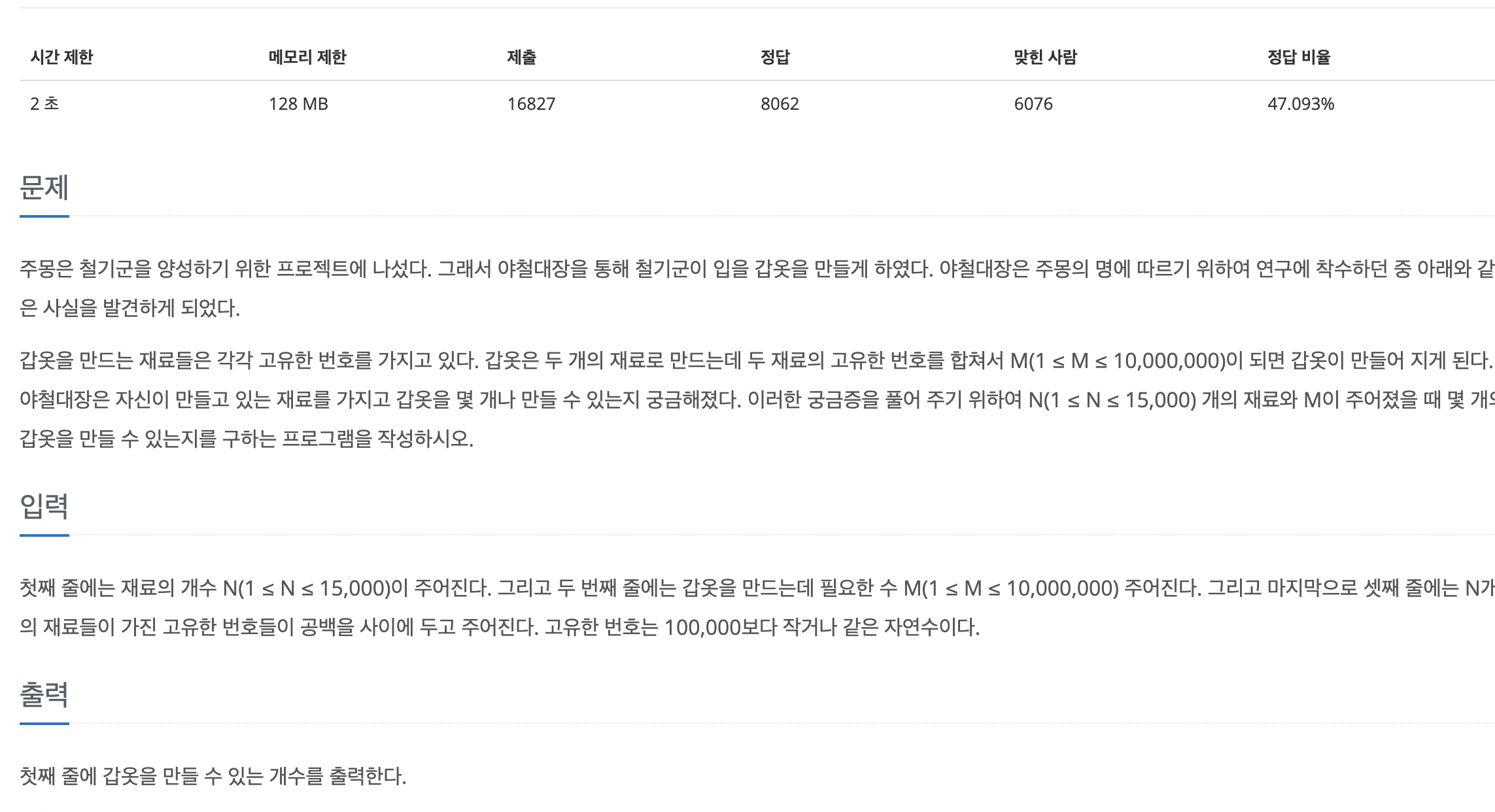
마찬가지로 간단한 투포인터 알고리즘. 위의 문제와 다른 것은 "2개"만 더하라는 것.

    public static class BOJ1940 {

        public static void main(String[] args) throws IOException {
            BufferedReader br = 
            new BufferedReader(new InputStreamReader(System.in));
            BufferedWriter bw = 
            new BufferedWriter(new OutputStreamWriter(System.out));

            int N = Integer.parseInt(br.readLine());
            int M = Integer.parseInt(br.readLine());
            int[] arr = new int[N];

            StringTokenizer st = new StringTokenizer(br.readLine());
            for(int i=0; i<N; i++) {
                arr[i] = Integer.parseInt(st.nextToken());
            }

            Arrays.sort(arr);

            int i=0, j=arr.length-1;
            int cnt = 0;

            while(i < j) {
                if(arr[i] + arr[j] == M) {
                    i++;
                    j--;
                    cnt++;
                }
                else {
                    if(arr[i] + arr[j] > M) {
                        j--;
                    }
                    else {
                        i++;
                    }
                }
            }

            bw.write(String.valueOf(cnt));

            br.close();
            bw.close();
        }
    }

• 투포인터 사용하기 위해 먼저 Arrays.sort()
• 맨 앞과 끝을 서로 더해가면서 찾는다(2개씩만)
• i + j == 일경우 양쪽에서 하나 좁힌다
• i + j > M 일경우 오른쪽에서 하나 내려온다
• i + j < M 일경우 왼쪽에서 하나 올라간다

---

생각보다 까다롭다. 더 풀어보자