개요 - 누적합이란?
- 제시된 구간의 합을 쉽게 구하기 위해서 사용하는 녀석으로써
- 입력 값의 범위가 매우 넓을 시, 구간의 합을 매번 구하는 것은 비효율적이다(10만만큼 100번한다고 생각해보자)
- 따라서 누적합을 먼저 계산 후 선언, 그것을 사용해서 구간 합을 구한다.
핵심 아이디어는 아래와 같다. 코드로 보자면,
public static void main(String[] args) {
int[] arr = {3, 1, 7, 4, 2, 9};
// 입력값 명시 선언
int[] prefixSum = new int[arr.length];
// 누적합 배열 선언
prefixSum[0] = arr[0];
// 누적합 배열의 0번 인덱스는 입력값 배열의 0번인덱스와 같음
for (int i = 1; i < arr.length; i++) {
prefixSum[i] = prefixSum[i-1] + arr[i];
// 누적 합 하는 부분 {3, 4, 11, 15, 17, 26}
}
for (int i = 0; i < prefixSum.length; i++) {
System.out.print(prefixSum[i] + " ");
//-> {3, 4, 11, 15, 17, 26}
}
System.out.println();
}- 위와 같이 가능하다
- 예를 들어 문제가, 어레이의 1번부터 3번까지의 "구간 합"을 구하라?
- 1,7,4 세개의 합이므로 12이다.
public static int noPrefix(int startIdx, int endIdx){
int[] arr = {3, 1, 7, 4, 2, 9};
// 1, 3
int sum = 0;
for (int i = startIdx; i <= endIdx; i++) {
sum += arr[i];
}
return sum; // 12 (답 맞음)
}- 그러나 위 배열과같이 6개의 요소가 아닌, 10만개의 요소를 가진 배열을 순회해야 한다면?
- 매우 비효율적이다. 따라서 먼저 누적합을 선언 후, 누적합들의 차로 구간 합을 구하는 것이 훨씬 빠름
문제 링크(11659) - " 구간 합 구하기 "
풀이 (Do it 책 vs 내 풀이)
Do it 책 기반 풀이
public static class BOJ11659 {
static int[] array;
public static void main0(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
array = new int[n + 1];
for (int i = 1; i <= n; i++) { // i까지의 누적합 구하기
array[i] = array[i - 1] + Integer.parseInt(st.nextToken());
System.out.println(array[i]);
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
// a, b사이의 구간합은 array[b]-array[a-1]과 같다
System.out.println(array[b]-array[a-1]);
}
}
}
}- 누적 합 구하기 위한 배열 선언 시, n+1 만큼의 배열 크기 정의
- 그를 통해서 누적합은 0번 인덱스가 존재하지 않고, 1번 인덱스 = arr[0], 2번부터 누적합 발생
- 따라서 계산시 array[b] - array[a-1] 계산해서 값 도출 가능
그러나, 0번 인덱스가 존재하지 않는 점과 어레이의 길이가 다르다는 점이 좀 마음에 안들었음. 그리고 결정적으로, 책에서 아이디어만 보고 풀었어서 dp에서 썼던 [0]번 인덱스 먼저 선언하고 채워가는 식으로 구현해봄.
나의 풀이
...
// https://www.acmicpc.net/problem/11659
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt(); // 배열의 길이
int N = sc.nextInt(); // 구간합 구해야 하는 개수
int[] arr = new int[M];
for (int i = 0; i < M; i++) {
arr[i] = sc.nextInt();
}
int[] preFixSum = new int[M];
preFixSum[0] = arr[0];
// 5,4,3,2,1 인 경우
// prefixSum[0] = 5;
// prefixSum[1] = 5 + 4 = 9
// prefixSum[2] = 9 + 3 = 12
// ... 14
// prefixSum[4] = 14 + 1 = 15
for (int i = 1; i < arr.length; i++) {
preFixSum[i] = preFixSum[i - 1] + arr[i];
}
for (int i = 0; i < N; i++) {
int from = sc.nextInt();
int to = sc.nextInt();
// 1 3 : 12 --> 12
// 2 4: 9 --> 14 - 5 = 9
// 구간합 계산
// 인덱스를 0부터 해서 toIdx -1, from 인덱스는 1 이상일경우 -2, 아니면 0
int sum = preFixSum[to - 1] - (from > 1 ? preFixSum[from - 2] : 0);
System.out.println(sum);
}
}- 위와 같이, 구간 합 예시를 보면 계산이 가능함
- to인덱스에서 -1, 그리고 from인덱스에서 -2 해야하는데, 1 이상인 경우만 그리 함
- 왜 이런 작업이 발생하는가? 인덱스 자체가 동일하므로 다시 한번 가공을 거쳐야함(렝스 위주로 계산되기 때문에)
문제 링크 - 2259 "수열"
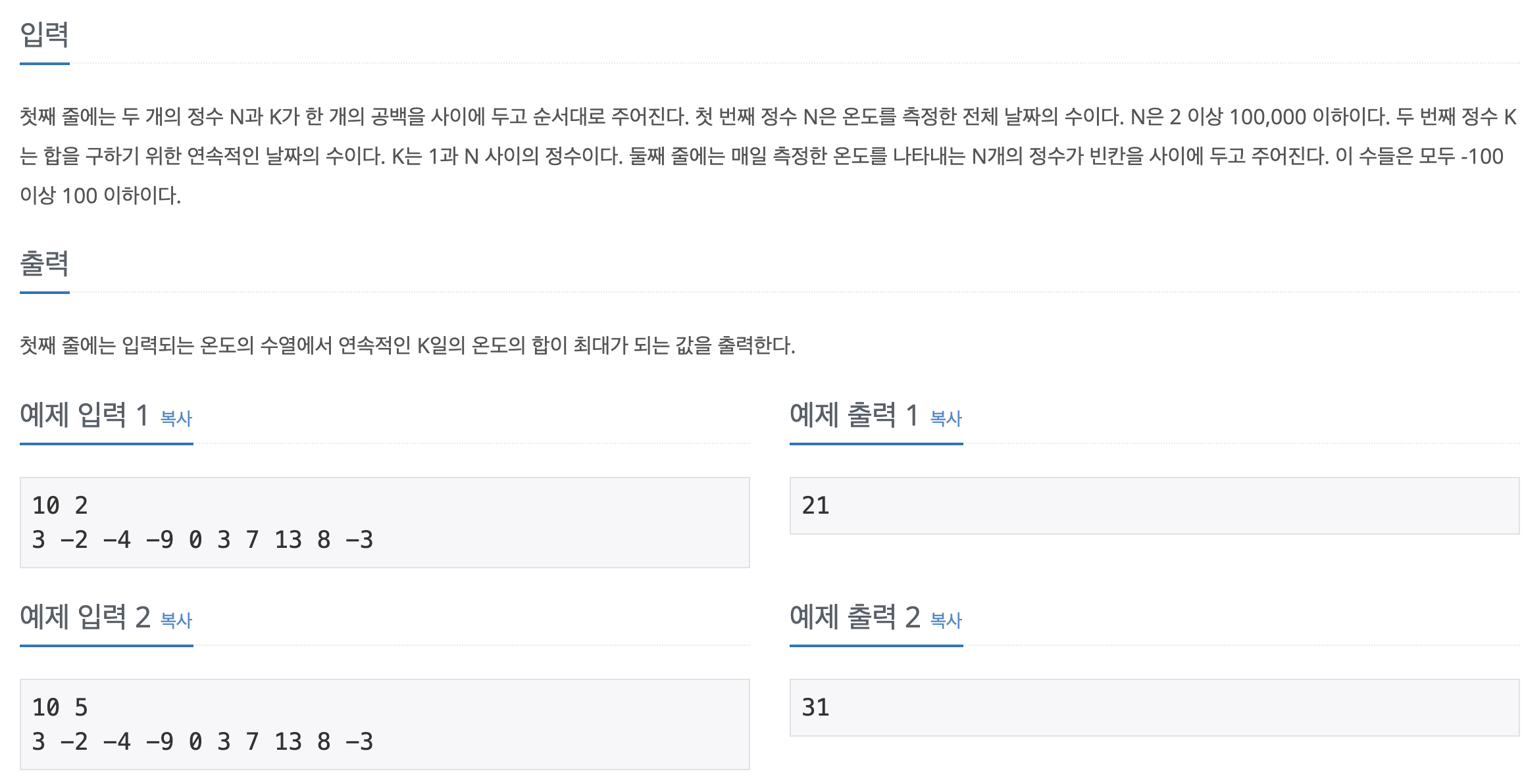
나의 풀이(맞은 풀이)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BOJ2559{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 전체 날짜 수
int K = Integer.parseInt(st.nextToken()); // 구간 합
// 5, 3 -> 0,1,2 // 1,2,3 // 2,3,4
// 0,1,2 맞네
int[] arr = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < arr.length; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int[] prefixSum = new int[N];
prefixSum[0] = arr[0];
for (int i = 1; i < N; i++) {
prefixSum[i] = prefixSum[i-1] + arr[i];
}
// int max = 0; // 0으로 하면 틀림.
int max = Integer.MIN_VALUE;
//10 2 --> 21
//1 2 3 4 5 6 7 8 9 10
//3 -2 -4 -9 0 3 7 13 8 -3
// 9+8이 젤큼
//21
//1 2 3 4 5 6 7 8 9 10
//3, 1, -3, -12, -12, -9, -2, 11, 19, 16
// 아이가 7이라면?
// 8번 인덱스, 7번 인덱스
for (int i = 0; i < prefixSum.length - K + 1; i++) {
int sum = prefixSum[i + K - 1] - (i > 0 ? prefixSum[i - 1] : 0);
if (sum > max){
max = sum;
}
}
System.out.println(max);
}
}- 젤 중요했던 부분은 마찬가지로 출력부분(누적합에서 적절한 의미 찾는 부분)
- 바로 이부분이다
...
for (int i = 0; i < prefixSum.length - K + 1; i++) {
int sum = prefixSum[i + K - 1] - (i > 0 ? prefixSum[i - 1] : 0);
if (sum > max){
max = sum;
}
}
System.out.println(max);
}
...- 예를 들어, 예시와 같이 N이 10이고 K가 2라면
- 1+2, 2+3 등 수같이 "2개"만 정해서 합쳐야한다. 그러나 인덱스에서 -2 만큼의 차이에 모두 들어가는 누적합은 3개가 된다
- 따라서, i + K " -1" 해 준 값에, (i > 0 ? prefixSum[i - 1] : 0); 를 뺴준다(0번에서 k-1번까지의 합은 무엇인가를 빼줄 필요가 없으므로)
정리
- 누적합을 쓰는 이유는 구간 합을 구할 때, 먼저 배열의 길이만큼의 연산을 통해서 누적합을 선언하고, 누적합들의 차이로 구간합을 구하는 것이 훨씬 유리하기 때문
- dp 개념이랑도 (Tabulation) 비슷하다.
