로지스틱 회귀

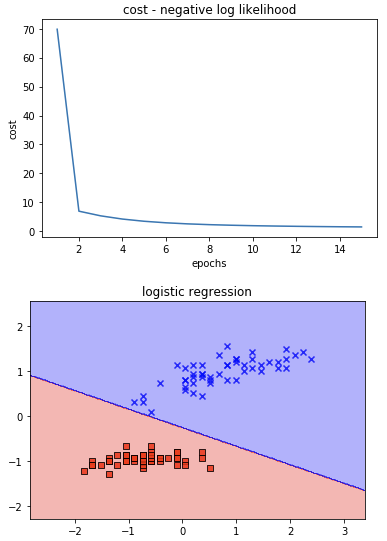
로지스틱 회귀 logistic regression

선형 회귀 방식을 이용한 이진 분류 모델

로지스틱 시그모이드 함수 logistic sigmoid function

• 오즈 비 odds ratio: 특정 이벤트가 발생할 확률이 그렇지 않을 확률의 몇배인가? (여기서 특정 이벤트: $y=1$)

  • $odds\_ratio=\frac{p(y=1|x)}{1-p(y=1|x)}$
  • 오즈 비의 출력값의 범위: $\left[0, +\infin\right)$

• 로짓 함수: 오즈 비의 입력값 $p$의 범위가 [0, 1]일 때, $(-\infin, +\infin)$ 범위의 출력을 얻기 위해 오즈 비에 로그를 덧씌운다.

  • $logit(p)=ln\frac{p}{1-p}$
  • 선형 회귀 방식을 이용하여 독립변수의 선형결합으로 logit값을 예측한다.
    $\quad logit(P(y=1|x))=w_0x_0+\cdots+w_mx_m=\sum_{i=0}^m w_ix_i = \boldsymbol{w}^\top\boldsymbol{x} = z$

• 로지스틱 시그모이드 함수: 데이터 샘플의 레이블을 예측하기 위해선 $\boldsymbol{x}$를 입력으로 받아 $P(y=1|x)$, 레이블이 1일 확률을 계산해야하므로 로짓 함수를 $\boldsymbol{x}$를 입력받아 $p$를 출력하도록 역함수를 취한다. 짧게 시그모이드 함수.
  • $p_i=logit^{-1}(\boldsymbol{w}^\top\boldsymbol{x})=\frac{1}{1+e^{-\boldsymbol{w}^\top\boldsymbol{x}}} = \frac{1}{1+e^{-z}}$
  • 특정 샘플의 실수 로짓값을 입력받아 $y=1$일 확률값을 출력한다.
    • $z\rightarrow\infin$: 오즈비가 매우 크다. $y=1$일 확률이 1에 가까워진다. = 시그모이드 함수 값이 1에 가까워진다.
    • $z\rightarrow-\infin$: 오즈비가 매우 작다. $y=1$일 확률이 0에 가까워진다. = 시그모이드 함수 값이 0에 가까워진다.
      

로지스틱 회귀 모델

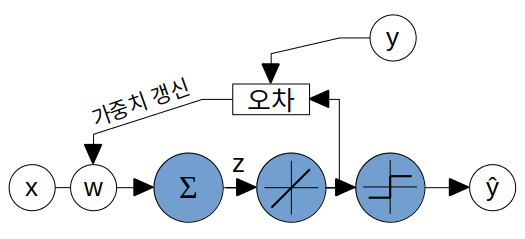
ADALINE과 비교

• ADALINE
  
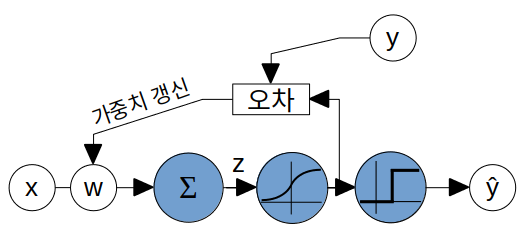
• 로지스틱 회귀 모델: 아달린의 선형 함수를 시그모이드 함수로 대체
  

시그모이드 함수의 해석

$\boldsymbol{x}$에 대한 시그모이드 함수의 출력은 $\boldsymbol{x}$의 레이블 $y$가 1일 확률 $\phi(z)=P(y=1|\boldsymbol{x};\boldsymbol{w})$
어떤 샘플에 대해서 $\phi(z)=0.7$이라면 이 샘플이 클래스1에 속할 확률이 70%라고 해석한다.
클래스 0에 속할 확률 $P(y=0|\boldsymbol{x};\boldsymbol{w})=1-\phi(z)$

임계함수

시그모이드 함수의 출력을 이진 출력으로 변환.
어떤 클래스에 속할 확률(시그모이드 함수 출력값)이 50% 이상이면 그 클래스를 반환.

$\hat{y}=\left\{\begin{matrix}1,&\phi(z)\ge0.5\\0,&otherwise\end{matrix}\right.$

$\hat{y}=\left\{\begin{matrix}1,&z\ge0.\\0,&otherwise\end{matrix}\right.$

가능도 likelihood L

$L(\boldsymbol{w})=P(\boldsymbol{y}|\boldsymbol{x};\boldsymbol{w})=\prod_{i=1}^n P(y^{(i)}|\boldsymbol{x}^{(i)};\boldsymbol{w})=\prod_{i=1}^n(\phi(z^{(i)}))^{y^{(i)}}(1-\phi(z^{(i)}))^{1-y^{(i)}}$

시그모이드 함수로 계산한 개별 샘플들이 각자의 레이블에 속할 확률의 곱
모든 샘플들이 각자의 레이블에 속할 확률이 100%라면 $L=1$로 최댓값

• $y^{(i)}=1$인 샘플 $\boldsymbol{x}^{(i)}$에 대해서
  • $(\phi(z^{(i)}))^{y^{(i)}}$: $\boldsymbol{x}^{(i)}$의 클래스가 1일 확률에 대한 항으로 1에 가까워져야한다.
  • $(1-\phi(z^{(i)}))^{1-y^{(i)}}$: $\boldsymbol{x}^{(i)}$의 클래스가 0일 확률. 다만 $y^{(i)}=1$인 경우 확률값을 $1-y^{(i)}=0$제곱하여 1이 되므로 무시된다.
• $y^{(i)}=0$인 경우에는 반대로 $(\phi(z^{(i)}))^{y^{(i)}}$, 샘플이 클래스 1에 속할 확률이 무시되고 $(1-\phi(z^{(i)}))^{1-y^{(i)}}$, 샘플이 클래스 0에 속할 확률이 가능도 계산에 포함된다.

가능도를 최대화하는 방향으로 가중치를 업데이트한다. (가능도의 최대화 = '모델이 계산한 개별 샘플들이 각자의 클래스에 속할 확률'의 최대화)

가능도에 로그를 씌울 경우

1. 가능도가 매우 작아 발생하는 언더플로우 방지: $0\le\phi(z)\le1$ 이므로 계속 곱할 경우 매우 작아진다.
2. 계수의 곱을 합으로 바꾼다.

$l(\boldsymbol{w})=logL(\boldsymbol{w})=\sum_{i=1}^n\left[y^{(i)}log(\phi(z^{(i)}))+\left(1-y^{(i)}\right)log(1-\phi(z^{(i)}))\right]$

• $y^{(i)}=1$일 때, $log(\phi(z^{(i)}))$만 더해진다.
• $y^{(i)}=0$일 때, $log(1-\phi(z^{(i)}))$만 더해진다.

로그 가능도에 $-1$을 곱해 최소화해야하는 비용함수로 사용할 수 있다.
$J(\boldsymbol{w})=-\sum_{i=1}^n\left[y^{(i)}log(\phi(z^{(i)}))+\left(1-y^{(i)}\right)log(1-\phi(z^{(i)}))\right]$

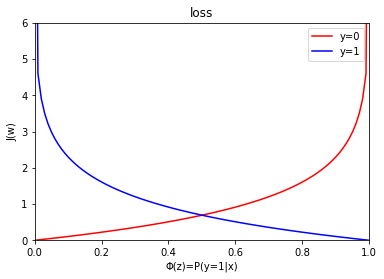
이 경우 개별 샘플에 대해서 다음과 같이 loss가 계산되고 에러가 클수록 더 큰 비용을 부과하게된다.
$J(\phi(z), y;\boldsymbol{w})=\begin{cases}-log(\phi(z)),&y=1\\-log(1-\phi(z)), &y=0\end{cases}$

가중치 갱신 - 경사 하강법

$\Delta w_{j} = -\eta{\partial J \over \partial\phi(z)}{\partial\phi(z)\over\partial z}{\partial z\over \partial w_{j}}$

${\partial\phi(z)\over\partial z}={\partial\over\partial z}{1 \over 1+e^{-z}}=({1\over 1+e^{-z}})^2e^{-z}={1 \over 1+e^{-z}}{e^{-z} \over 1+e^{-z}}=\phi(z)(1-\phi(z))$

$\Delta w_{j}=\eta\sum_{i=1}^n\left[y^{(i)}{1\over\phi(z^{(i)})}-\left(1-y^{(i)}\right){1\over 1-\phi(z^{(i)})}\right]\phi(z^{(i)})(1-\phi(z^{(i)}))x^{(i)}_j=\eta\sum_{i=1}^n(y^{(i)}-\phi(z^{(i)}))x^{(i)}_j$

$w_j=w_j+\Delta w_j=w_j+\eta\sum_{i=1}^n(y^{(i)}-\phi(z^{(i)}))x^{(i)}_j$

$\boldsymbol{w} = \boldsymbol{w} + \Delta\boldsymbol{w}=\boldsymbol{w}-\eta\nabla J(\boldsymbol{w})=\boldsymbol{w}+\eta\sum_{i=1}^n(y^{(i)}-\phi(z^{(i)}))\boldsymbol{x}^{(i)}$

코드

https://github.com/canlion/ml_study/blob/main/3_1_logistic_regression.ipynb