선형대수.5 - 선형변환_3

다시 공부 중...·2021년 11월 24일
선형대수책:mml
0

기저 변환

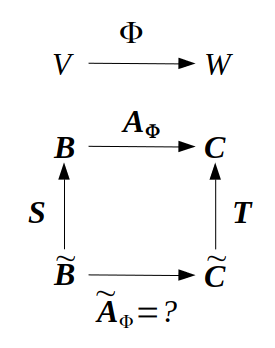
벡터 공간 VV와 기저 B=(b1,⋯ ,bn),B~=(b~1,⋯ ,b~n)B=(\boldsymbol{b}_1, \cdots, \boldsymbol{b}_n), \tilde{B}=(\tilde{\boldsymbol{b}}_1, \cdots, \tilde{\boldsymbol{b}}_n),
벡터공간 WW와 기저 C=(c1,⋯ ,cm),C~=(c~1,⋯ ,c~m)C=(\boldsymbol{c}_1, \cdots, \boldsymbol{c}_m), \tilde{C}=(\tilde{\boldsymbol{c}}_1, \cdots, \tilde{\boldsymbol{c}}_m),
선형 변환 Φ:V→W\Phi:V\rightarrow W와 기저 B,CB, C에 대한 변환행렬 AΦ\boldsymbol{A}_{\Phi},
선형 변환 Φ:V→W\Phi:V\rightarrow W와 기저 B~,C~\tilde{B}, \tilde{C}에 대한 변환행렬 A~Φ\tilde{\boldsymbol{A}}_{\Phi} 일 때,

❓: AΦ\boldsymbol{A}_\Phi와 A~Φ\tilde{\boldsymbol{A}}_\Phi의 관계

b~j=s1jb1+⋯+snjbn=∑i=1nsijbi\tilde{\boldsymbol{b}}_j=s_{1j}\boldsymbol{b}_1+\cdots+s_{nj}\boldsymbol{b}_n=\sum_{i=1}^{n} s_{ij}\boldsymbol{b}_i ➡ 변환행렬 S\boldsymbol{S}: 기저 B~\tilde{\boldsymbol{B}}에 대한 좌표를 기저B\boldsymbol{B}에 대한 좌표로 변환
c~k=t1kc1+⋯+tmkcm=∑l=1mtlkcl\tilde{\boldsymbol{c}}_k=t_{1k}\boldsymbol{c}_1+\cdots+t_{mk}\boldsymbol{c}_m=\sum_{l=1}^{m} t_{lk}\boldsymbol{c}_l ➡ 변환행렬 T\boldsymbol{T}: 기저 C~\tilde{\boldsymbol{C}}에 대한 좌표를 기저C\boldsymbol{C}에 대한 좌표로 변환

1) 먼저 B~\tilde{B}를 C~\tilde{C}를 경유해서 CC로 표현해본다.
Φ(b~j)=∑k=1mα~kjc~k=∑k=1mα~kj∑l=1mtlkcl=∑l=1m(∑k=1mtlkα~kj)cl\Phi(\tilde{\boldsymbol{b}}_j)=\sum_{k=1}^m \tilde{\alpha}_{kj}\tilde{\boldsymbol{c}}_k=\sum_{k=1}^m \tilde{\alpha}_{kj}\sum_{l=1}^{m}t_{lk}\boldsymbol{c}_l=\sum_{l=1}^{m}\left(\sum_{k=1}^m t_{lk}\tilde{\alpha}_{kj}\right)\boldsymbol{c}_l

2) 다음은 B~\tilde{B}를 BB를 경유해서 CC로 표현해본다.
Φ(b~j)=Φ(∑i=1nsijbi)=∑i=1nsijΦ(bi)=∑i=1nsij∑l=1mαlicl=∑l=1m(∑i=1nαlisij)cl\Phi(\tilde{\boldsymbol{b}}_j)=\Phi\left(\sum_{i=1}^n s_{ij}\boldsymbol{b}_i\right)=\sum_{i=1}^n s_{ij}\Phi(\boldsymbol{b}_i)=\sum_{i=1}^n s_{ij}\sum_{l=1}^m \alpha_{li}\boldsymbol{c}_l=\sum_{l=1}^m(\sum_{i=1}^n \alpha_{li}s_{ij})\boldsymbol{c}_l

3) ∑k=1mtlkα~kj=∑i=1nαlisij\sum_{k=1}^m t_{lk}\tilde{\alpha}_{kj}=\sum_{i=1}^n \alpha_{li}s_{ij}\quad ➡ TA~Φ=AΦS\quad\boldsymbol{T}\tilde{\boldsymbol{A}}_\Phi=\boldsymbol{A}_\Phi\boldsymbol{S}\quad ➡ A~Φ=T−1AΦS\quad\tilde{\boldsymbol{A}}_\Phi=\boldsymbol{T}^{-1}\boldsymbol{A}_\Phi\boldsymbol{S}

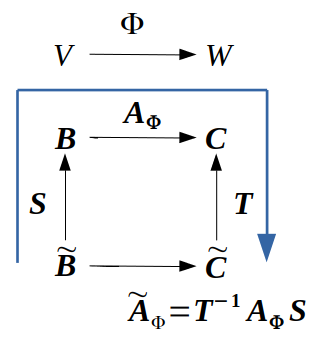
📌 A~=T−1AS\tilde{\boldsymbol{A}}=\boldsymbol{T}^{-1}\boldsymbol{AS} 를 만족하는 T∈Rm×m\boldsymbol{T}\in\mathbb{R}^{m\times m}, S∈Rn×n\boldsymbol{S}\in\mathbb{R}^{n\times n} 이 존재하면 A,A~\boldsymbol{A}, \tilde{\boldsymbol{A}} 는 서로 equivalent하다고 한다.
📌 A~=S−1AS\tilde{\boldsymbol{A}}=\boldsymbol{S}^{-1}\boldsymbol{AS} 를 만족하는 S∈Rn×n\boldsymbol{S}\in\mathbb{R}^{n\times n} 이 존재하면 A,A~∈Rn×n\boldsymbol{A}, \tilde{\boldsymbol{A}} \in \mathbb{R}^{n \times n}은 similar, 서로 닮음 이라고 한다.

  • 닮은 행렬들은 항상 equivalent하지만 equivalent한 행렬들이 항상 닮은 행렬은 아니다.

Image, Kernel

선형 변환의 image와 kernel은 어떤 특징을 가진 벡터 공간

📌 Φ:V→W\Phi: V\rightarrow W 에 대해서

  • kernel, null space:
    ker(Φ):=Φ−1(0W)={v∈V:Φ(v)=0W}\mathrm{ker}(\Phi) := \Phi^{-1}(\boldsymbol{0}_{W})=\left\{\boldsymbol{v}\in V:\Phi(\boldsymbol{v})=\boldsymbol{0}_W\right\}
    🤔 변환시에 0\boldsymbol{0}이 되는 VV의 벡터들. AΦx=0\boldsymbol{A}_{\Phi}\boldsymbol{x}=\boldsymbol{0}의 해.

  • image, range:
    Im(Φ):=Φ(V)={w∈W∣∃v∈V:Φ(v)=w}\mathrm{Im}(\Phi):=\Phi(V)=\left\{\boldsymbol{w}\in W|\exist\boldsymbol{v}\in V:\Phi(\boldsymbol{v})=\boldsymbol{w}\right\}
    🤔 변환으로 VV의 벡터들과 맵핑되는 WW의 벡터들의 집합. 변환으로 VV에서 도달할 수 있는 WW의 벡터들.

  • VV를 Φ\Phi의 domain, WW를 Φ\Phi의 codomain이라 한다.

📌 Φ:V→W\Phi:V\rightarrow W가 선형 변환, V,WV, W가 벡터공간일 때

  • Φ(0V)=0W\Phi(\boldsymbol{0}_V)=\boldsymbol{0}_W를 항상 만족하므로 0V∈ker(Φ)\boldsymbol{0}_V\in \mathrm{ker} (\Phi). 그러므로 kernel은 공집합이 아니다.
    🤔 AΦx=0\boldsymbol{A}_{\Phi}\boldsymbol{x}=\boldsymbol{0} 의 자명한 해 0\boldsymbol{0}

  • Im(Φ)⊆W\mathrm{Im}(\Phi)\subseteq W 는 WW의 부분공간, ker(Φ)⊆V\mathrm{ker}(\Phi)\subseteq V는 VV의 부분 공간.
    🤔 image와 kernel 모두 0\boldsymbol{0}를 포함하고 Φ\Phi가 선형 변환이면 image의 경우 Φ(αv1)+Φ(βv2)=w1+w2=w=Φ(αv1+βv2)\Phi(\alpha\boldsymbol{v}_1)+\Phi(\beta\boldsymbol{v}_2) = \boldsymbol{w}_1+\boldsymbol{w}_2=\boldsymbol{w}=\Phi(\alpha\boldsymbol{v}_1+\beta\boldsymbol{v}_2) 이므로 w1,w2∈Im(Φ)\boldsymbol{w}_1,\boldsymbol{w}_2\in\mathrm{Im}(\Phi) 일 때,w∈Im(Φ)\boldsymbol{w}\in\mathrm{Im}(\Phi) / kernel의 경우 Φ(αv1)+Φ(βv2)=Φ(αv1+βv2)=0\Phi(\alpha\boldsymbol{v}_1) + \Phi(\beta\boldsymbol{v}_2) = \Phi(\alpha\boldsymbol{v}_1+\beta\boldsymbol{v}_2)=\boldsymbol{0} 으로 v1,v2∈ker(Φ)\boldsymbol{v}_1,\boldsymbol{v}_2\in\mathrm{ker}(\Phi) 일 때, αv1+βv2∈ker(Φ)\alpha\boldsymbol{v}_1+\beta\boldsymbol{v}_2\in\mathrm{ker}(\Phi)이므로 image, kerenl 모두 벡터 합과 스칼라의 곱에 닫혀있음.

  • Φ\Phi는 injective, 단사   ⟺  ker(Φ)={0}\iff \mathrm{ker}(\Phi)=\{\boldsymbol{0}\}
    🤔 일단 0∈ker(Φ)\boldsymbol{0}\in\mathrm{ker}(\Phi)이므로 Φ\Phi가 단사인 경우 ker(Φ)={0}\mathrm{ker}(\Phi)=\{\boldsymbol{0}\} / 단사임을 보이려면 Φ(a)=Φ(b)\Phi(a)=\Phi(b)일 때, a=ba=b를 보여야함. Φ(a)=Φ(b)\Phi(\boldsymbol{a})=\Phi(\boldsymbol{b})라면 Φ(a)−Φ(b)=Φ(a−b)=0\Phi(\boldsymbol{a})-\Phi(\boldsymbol{b})=\Phi(\boldsymbol{a}-\boldsymbol{b})=\boldsymbol{0}. 여기서 ker(Φ)={0}\mathrm{ker}(\Phi)=\{\boldsymbol{0}\}이면 a−b=0\boldsymbol{a}-\boldsymbol{b}=\boldsymbol{0}, a=b\boldsymbol{a}=\boldsymbol{b}. 단사.

📌 A∈Rm×n\boldsymbol{A}\in\mathbb{R}^{m\times n}, 선형 변환 Φ:Rn→Rm,x↦Ax\Phi:\mathbb{R}^n\rightarrow\mathbb{R}^m, \boldsymbol{x}\mapsto\boldsymbol{Ax} 일 때,

  • A=[a1,⋯ ,an]\boldsymbol{A}=\left[\boldsymbol{a}_1, \cdots, \boldsymbol{a}_n\right] 일 때,
    Im(Φ)={Ax:x∈Rn}={∑i=1nxiai:x1,⋯ ,xn∈R}=span[a1,⋯ ,an]⊆Rm\mathrm{Im}(\Phi)=\{\boldsymbol{Ax}:\boldsymbol{x}\in\mathbb{R}^n\}=\{\sum_{i=1}^n x_i \boldsymbol{a}_i:x_1, \cdots, x_n \in \mathbb{R}\}=\mathrm{span}[\boldsymbol{a}_1, \cdots, \boldsymbol{a}_n]\subseteq \mathbb{R}^m
    image는 A\boldsymbol{A}의 열들의 span으로 column space, 열공간이라고도 한다. Rm\mathbb{R}^m의 부분공간.

  • rk(A)=dim(Im(Φ))\mathrm{rk}(\boldsymbol{A})=\mathrm{dim}(\mathrm{Im}(\Phi))
    🤔 rank는 행렬의 피벗열의 수 = 선형 독립인 열의 수 = 행렬의 열들로 구성하는 벡터 공간의 기저의 수

  • ker(Φ)\mathrm{ker}(\Phi)는 homogeneous, 동차연립방정식 Ax=0\boldsymbol{Ax}=\boldsymbol{0}의 일반해로 0∈Rm\boldsymbol{0}\in\mathbb{R}^m을 만드는 모든 선형 결합이다.

  • ker(Φ)\mathrm{ker}(\Phi)는 Rn\mathbb{R}^n의 부분 공간이고 (nn은 A\boldsymbol{A}의 열의 수) 행렬의 열들간의 관계를 나타낸다. = 행렬의 열들의 선형 종속 여부를 알 수 있다.
    🤔 Ax=0\boldsymbol{Ax}=\boldsymbol{0} 의 해를 구하는 방식이 행렬의 어떤 열을 다른 열들로 표현하여 0\boldsymbol{0}을 만드는 방식이었다.

📖 Φ:R4→R2\Phi:\mathbb{R}^4 \rightarrow \mathbb{R}^2, [x1x2x3x4]↦[12−101001][x1x2x3x4]\begin{bmatrix}x_1\\x_2\\x_3\\x_4\end{bmatrix}\mapsto\begin{bmatrix}1&2&-1&0\\1&0&0&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\\x_4\end{bmatrix}일 때,

Im(Φ)=span[[11],[20],[−10],[01]]⊂R2\mathrm{Im}(\Phi)=\mathrm{span}[\begin{bmatrix}1\\1\end{bmatrix}, \begin{bmatrix}2\\0\end{bmatrix}, \begin{bmatrix}-1\\0\end{bmatrix}, \begin{bmatrix}0\\1\end{bmatrix}] \subset \mathbb{R}^2 / image는 codomain의 부분공간으로 변환행렬의 열들의 선형 결합 집합.

ker(Φ)\mathrm{ker}(\Phi)를 구하려면 Ax=0\boldsymbol{Ax}=\boldsymbol{0}을 푼다.
변환 행렬을 기약 사다리꼴로 변환하고
[12−101001]⇝⋯⇝[100101−12−12]\begin{bmatrix}1&2&-1&0\\1&0&0&1\end{bmatrix} \rightsquigarrow\cdots\rightsquigarrow \begin{bmatrix}1&0&0&1\\0&1&-\frac{1}{2}&-\frac{1}{2}\end{bmatrix}
피벗열이 아닌 열들을 좌측의 피벗열들로 표현하여 상쇄해 0\boldsymbol{0}을 만든다.
ker(Φ)=span[[01210],[−11201]]⊂R4\mathrm{ker}(\Phi)=\mathrm{span}[\begin{bmatrix}0\\\frac{1}{2}\\1\\0\end{bmatrix},\begin{bmatrix}-1\\\frac{1}{2}\\0\\1\end{bmatrix}]\subset \mathbb{R}^4 / kernel은 domain의 부분공간.

📌 Rank-Nullity 정리
벡터공간 V,WV, W, 선형 변환 Φ:V→W\Phi:V\rightarrow W일 때, dim(ker(Φ)))+dim(Im(Φ))=dim(V)\mathrm{dim}(\mathrm{ker}(\Phi))) + \mathrm{dim}(\mathrm{Im}(\Phi)) = \mathrm{dim}(V)

dim(V)=n,dim(ker(Φ))=k\mathrm{dim}(V)=n, \mathrm{dim}(\mathrm{ker}(\Phi))=k일 때, dim(Im(Φ))=n−k\mathrm{dim}(\mathrm{Im}(\Phi))=n-k임을 보여야한다.
VV의 기저가 (b1,⋯ ,bn)(\boldsymbol{b}_1, \cdots, \boldsymbol{b}_n)일 때,
Im(Φ)=span[Φ(b1),⋯ ,Φ(bn)]\qquad\mathrm{Im}(\Phi)=\mathrm{span}[\Phi(\boldsymbol{b}_1), \cdots, \Phi(\boldsymbol{b}_n)]
여기서 ker(Φ)\mathrm{ker}(\Phi)의 기저가 (b1,⋯ ,bk)(\boldsymbol{b}_1, \cdots, \boldsymbol{b}_k)이라면 Φ(b1)=⋯=Φ(bk)=0\Phi(\boldsymbol{b}_1) = \cdots = \Phi(\boldsymbol{b}_k) = \boldsymbol{0} 이므로
Im(Φ)=span[Φ(bk+1),⋯ ,Φ(bn)]\qquad\mathrm{Im}(\Phi)=\mathrm{span}[\Phi(\boldsymbol{b}_{k+1}), \cdots, \Phi(\boldsymbol{b}_n)]
Φ(bk+1),⋯ ,Φ(bn)\Phi(\boldsymbol{b}_{k+1}), \cdots, \Phi(\boldsymbol{b}_n)가 기저이려면 선형 독립인지 확인해야한다.
∑i=k+1nαiΦ(bi)=Φ(∑i=k+1nαibi)=0\qquad\sum_{i=k+1}^n\alpha_i\Phi(\boldsymbol{b}_i)=\Phi(\sum_{i=k+1}^n \alpha_i \boldsymbol{b}_i)=\boldsymbol{0}
여기서 ∑i=k+1nαibi\sum_{i=k+1}^n \alpha_i \boldsymbol{b}_i는 ker(Φ)\mathrm{ker}(\Phi)의 원소이고 이는 ker(Φ)\mathrm{ker}(\Phi)의 기저 (b1,⋯ ,bk)(\boldsymbol{b}_1, \cdots, \boldsymbol{b}_k)의 선형 결합으로 표현할 수 있다.
∑i=k+1nαibi=∑j=1kβjbj\qquad\sum_{i=k+1}^n \alpha_i \boldsymbol{b}_i=\sum_{j=1}^k \beta_j \boldsymbol{b}_j
(b1,⋯ ,bn)(\boldsymbol{b}_1, \cdots, \boldsymbol{b}_n)은 VV의 기저이므로 ∀α,∀β=0\forall\alpha,\forall\beta=0으로 Φ(bk+1),⋯ ,Φ(bn)\Phi(\boldsymbol{b}_{k+1}), \cdots, \Phi(\boldsymbol{b}_n)는 선형 독립이며 Im(Φ)\mathrm{Im}(\Phi)의 기저이므로 dim(Im(Φ)))=n−k\mathrm{dim}(\mathrm{Im}(\Phi)))=n-k

  • dim(Im(Φ))<dim(V)\mathrm{dim}(\mathrm{Im}(\Phi)) < \mathrm{dim}(V)이면 ker(Φ)\mathrm{ker}(\Phi)는 0V\boldsymbol{0}_V 외의 원소를 갖고 dim(ker(Φ))≥1\mathrm{dim}(\mathrm{ker}(\Phi))\geq1
  • dim(Im(Φ))<dim(V)\mathrm{dim}(\mathrm{Im}(\Phi)) < \mathrm{dim}(V)이면 AΦx=0\boldsymbol{A}_\Phi\boldsymbol{x}=\boldsymbol{0}은 무수히 많은 해를 갖는다.
  • dim(V)=dim(W)\mathrm{dim}(V)=\mathrm{dim}(W)이면 Φ\Phi가 (injective 단사 / surjective 전사 / bijective 단전사)는 3방향 동치.
    🤔 단사라면 ker(Φ)={0}\mathrm{ker}(\Phi)=\{\boldsymbol{0}\}이므로 전사. 전사라면 dim(Im(Φ))=dim(W)\mathrm{dim}(\mathrm{Im}(\Phi))=\mathrm{dim}(W)이고 kernel의 차원 0으로 ker(Φ)={0}\mathrm{ker}(\Phi)=\{\boldsymbol{0}\}이고 단사. 그리고 전단사.
profile
다시 공부 중...
인공지능, 개발 공부
이전 포스트

로지스틱 회귀

다음 포스트

Big-O notation & sorting

0개의 댓글