핵심수학 메모

벡터

제2 cos 법칙

$\mathrm{cos}\theta_A=\frac{b^2+c^2-a^2}{2bc}$

두 벡터 사이의 각도

$\mathrm{cos}\theta=\frac{||\boldsymbol{x}||_2^2+||\boldsymbol{y}||_2^2-||\boldsymbol{y-x}||_2^2}{2||\boldsymbol{x}||_2||\boldsymbol{y}||_2}=\frac{<\boldsymbol{x, y}>}{||\boldsymbol{x}||_2||\boldsymbol{y}||_2}$
$<\boldsymbol{x, y}>=\sum_{i=1}^d x_i y_i$ 내적

내적

$<\boldsymbol{x, y}>=\sum_{i=1}^d x_i y_i=||\boldsymbol{x}||_2||\boldsymbol{y}||_2\mathrm{cos}\theta$
$\boldsymbol{x}$에서 $\boldsymbol{y}$ 위에 내린 정사영 $\mathrm{Proj}(\boldsymbol{x})$의 길이($||\boldsymbol{x}||_2\mathrm{cos}\theta$)에 $||\boldsymbol{y}||_2$를 곱한 값
두 벡터의 유사도 계산에 사용

---

행렬

넘파이의 inner 함수

$\boldsymbol{X}\in\mathbb{R}^{n\times l}, \boldsymbol{Y}\in\mathbb{R}^{m\times l}$, Z = np.inner(X, Y)이라면
$\boldsymbol{Z}=(\sum_k x_{ik}y_{jk})\in\mathbb{R}^{n\times m}$로 $\boldsymbol{X}$의 $i$번째 행과, $\boldsymbol{Y}$의 $j$번째 행을 내적한 값이 $\boldsymbol{Z}$의 $i$행, $j$열 성분
$\boldsymbol{Z}=\boldsymbol{XY}^\top$

X = np.array([  # 2x4
    [1, 2, 3, 4],
    [5, 6, 7, 8],
])

Y = np.array([  # 5x4
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
    [13, 14, 15, 16],
    [17, 18, 19, 20],
])

np.inner(X, Y)  # 2x5
# array([[ 30,  70, 110, 150, 190],
#        [ 70, 174, 278, 382, 486]])

np.matmul(X, Y.T)
# array([[ 30,  70, 110, 150, 190],
#        [ 70, 174, 278, 382, 486]])

넘파이의 np.linalg.inv: 역행렬 계산 함수

의사역행렬/유사역행렬/무어-펜로즈 역행렬

📌 행렬이 정사각행렬이 아닐때 이용
$\boldsymbol{A}\in\mathbb{R}^{n\times m}$

• $\boldsymbol{A}$의 행이 열보다 많을때, $n>m$
  $\boldsymbol{A}^+=(\boldsymbol{A}^\top\boldsymbol{A})^{-1}\boldsymbol{A}^\top$
  $\boldsymbol{A}^+\boldsymbol{A}=\boldsymbol{I}$
• $\boldsymbol{A}$의 열이 행보다 많을때, $n<m$
  $\boldsymbol{A}^+=\boldsymbol{A}^\top(\boldsymbol{A}\boldsymbol{A}^\top)^{-1}$
  $\boldsymbol{A}\boldsymbol{A}^+=\boldsymbol{I}$

📌 np.linalg.pinv(Y)

X = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8],
])

X_pinv = np.linalg.pinv(X)

X @ X_pinv  # 행<열 이므로 오른쪽에.
# array([[ 1.00000000e+00, -2.77555756e-16],
#        [ 1.33226763e-15,  1.00000000e+00]])

X_pinv @ X  # 반대쪽에 붙이면 틀린 결과
# array([[ 0.7,  0.4,  0.1, -0.2],
#        [ 0.4,  0.3,  0.2,  0.1],
#        [ 0.1,  0.2,  0.3,  0.4],
#        [-0.2,  0.1,  0.4,  0.7]])

📌 쓰임새

1. 연립방정식 풀이 - ???
   행보다 열이 많으면 유사역행렬을 오른쪽에 곱해야..?

2. 선형회귀 - 변수의 수보다 식의 수가 많은 경우 (행 > 열)
   $\boldsymbol{Xw}=\boldsymbol{y}$

   • 연립방정식은 풀리지 않음. 그러므로 $\boldsymbol{Xw}=\hat{\boldsymbol{y}}\approx\boldsymbol{y}$ 인 $\boldsymbol{w}$가 목표
   • $\boldsymbol{w}=\boldsymbol{X}^+\boldsymbol{y}$

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split


diabetes = load_diabetes()

X = diabetes['data']
X = (X-X.mean(axis=0)) / X.std(axis=0)
y = diabetes['target']
y = (y-y.mean()) / y.std()
print(X.shape, y.shape)
# (442, 10) (442,)

x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.1)

# =======================================================================
# == LinearRegression ===================================================
# =======================================================================

model = LinearRegression()
model.fit(x_train, y_train)
model.score(x_test, y_test)
# 0.4057564640105007

# =======================================================================
# == 유사역행렬 ==========================================================
# =======================================================================

x_train_ = np.concatenate([np.ones((x_train.shape[0], 1)), x_train], axis=-1)
x_test_ = np.concatenate([np.ones((x_test.shape[0], 1)), x_test], axis=-1)
x_train_ = np.concatenate([np.ones((x_train.shape[0], 1)), x_train], axis=-1)
x_test_ = np.concatenate([np.ones((x_test.shape[0], 1)), x_test], axis=-1)

w = np.linalg.pinv(x_train_) @ y_train

y_predict = x_test_ @ w

u = ((y_test - y_predict)**2).sum()
v = ((y_test - y_test.mean())**2).sum()
score = 1-u/v
print(score)
# 0.4057564640105006

이게 무슨 일이지 무슨 원리지

---

경사하강법-순한맛

$f(x)$값을 증가시키려면 $x=x+f'(x)$, 감소시키려면 $x=x-f'(x)$

편미분

$\partial_{\boldsymbol{x}_i}f(\boldsymbol{x})=\lim_{h \to 0} \frac{f(\boldsymbol{x}+h\boldsymbol{e}_i)-f(\boldsymbol{x})}{h}$, $\boldsymbol{e}$는 표준기저벡터

nabla $\nabla$
$\nabla f = (\partial_{\boldsymbol{x}_1}f, \cdots, \partial_{\boldsymbol{x}_d}f)$ : 그래디언트 벡터, 각 변수 별로 편미분한 값을 담은 벡터

딥러닝 학습법 이해하기

선형모델: $\boldsymbol{O}=\boldsymbol{XW}+\boldsymbol{b}$

$\boldsymbol{X}\in\mathbb{R}^{n\times d}, \boldsymbol{W}\in\mathbb{R}^{d\times p}$라면 $\boldsymbol{O}\in\mathbb{R}^{n\times p}$이고 이는 $p$개의 선형모델을 의미

softmax:

$\mathrm{softmax}(\boldsymbol{o})=(\frac{\mathrm{exp}(o_1)}{\sum_{k}^p \mathrm{exp}(o_k)}, \cdots, \frac{\mathrm{exp}(o_p)}{\sum_{k}^p \mathrm{exp}(o_k)})$
원소 간의 대소관계 유지되고, 상대적으로 작은 차이를 상대적으로 크게 만들어주고, 합이 1이되어 확률값으로 해석가능
분류에 주로 사용
지수함수 사용하므로 입력 벡터 중 너무 큰 값이 있다면 overflow 위험 존재. 그러므로 입력 벡터의 최댓값을 입력벡터에서 빼고 소프트맥스 계산. (대소관계 유지되므로 문제 없다.)
선형모델 + 소프트맥스 = 분류기

신경망:

비선형모델, 선형모델과 비선형 함수(활성 함수)들의 결합
선형모델의 출력에 활성 함수를 적용한 벡터 = 잠재벡터, 히든벡터, 뉴런

선형모델-활성함수-선형모델-활성함수-... 반복

활성함수

비선형 함수
비선형 함수 없이는 신경망은 선형모델과 차이 없음

• sigmoid:
  $\sigma(\boldsymbol{x})=\frac{1}{1+e^{-\boldsymbol{x}}}$
  
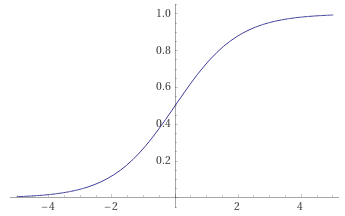
• tanh:
  $\tanh(\boldsymbol{x})=\frac{e^\boldsymbol{x}-e^{-\boldsymbol{x}}}{e^\boldsymbol{x}+e^{-\boldsymbol{x}}}$
  
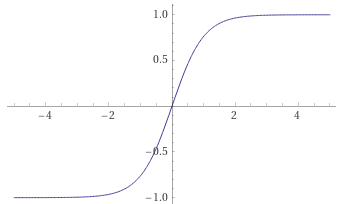
• ReLU
  $\mathrm{ReLU}(\boldsymbol{x})=\mathrm{max}\{0, \boldsymbol{x}\}$
  

층을 쌓는 이유

• 이론적으로는 2층으로 임의의 연속함수 근사 가능: universal approximation theorem
• 많은 레이어 = 목적 함수 근사에 필요한 뉴런 숫자 감소 = 효율적
  • 복잡한 목적 함수를 효율적으로 근사하려고

딥러닝의 학습: 역전파 알고리즘

• 손실함수를 각 가중치로 편미분하여 손실함수를 감소시키는 방향으로 가중치 갱신
• 체인룰 이용하여 출력층부터 입력층까지 그래디언트 차례로 계산, 전달 반복: 역전파
  • 체인룰 기반 자동미분
  • 각 레이어의 순전파 값을 보관해야하므로 역전파 알고리즘은 메모리 사용이 많다.

베이즈 통계학

조건부 확률을 이용하여 정보를 갱신하는 방법을 알려준다