Week3 : Normal approximation

• 많은 데이터는 위와 같은 bell-shaped 모양을 가진다.

경험적인 규칙(empirical rule)

• 어떤 데이터가 normal curve를 따른다고 해보자. 그렇다면, 데이터의 약 2/3 (68%)가 평균의 1 표준편차에 속한다.
• 마찬가지로 95%의 데이터는 평균의 2 표준편차에 속하며 99.7%는 3 표준편차에 속한다.
• 어떤 반의 키를 측정하였을 때, 이 데이터들은 normal curve를 따르고 평균이 $\bar x$=68.3, 표준편차가 $s$=1.8 로 계산된다고 해보자. 95%의 키 집합들을 구하라고 하면, 64.7≤x≤71.9 를 구할 수 있다 (68.3-1.8x2, 68.3+1.8x2).

Standardizing data

• A normal curve는 $\bar x$와 $s$로 결정된다. 만약, 데이터가 normal curve를 따른다고 하면, 우리는 $\bar x$와 $s$를 알고 있는 것이다.
• Normal curve의 면적을 계산하기 위해서, 우리는 데이터에 $\bar x$를 빼고 $s$ 로 나누는 작업을 한다. 이렇게 계산된 값을 $z$라고 하며, “standardized value or z-score” 라고 부른다.

• $z=2$는 average로부터 above한 2 stadard deviation라고 읽는다.

• 위 curve는 다음과 같은 함수로도 표현할 수 있다.

  $y = {1\over \sqrt 2\pi} e^{-{1\over2}x^2}$

• Normal approximation을 한다는 것은 normal curve의 영역을 구한다는 의미이다.

• 통계학자들이 정규분포의 면적을 계산해놓았다. 테이블은 이 링크(Standard Normal Table)에서 확인 가능하다, normal approximate 시에 항상 참고하면 되겠다.

위 z 수식을 다시 풀어보면 $x = \bar x + zs$ 이고, 따라서 30 percentile 의 heights(x)를 구하라고하고 table로부터 z=-0.52라고 주어졌다고 하면, 68.3 -0.52*1.8 = 67.4 가 된다.

Binominal settings

• 각 실험에서는 독립적인 시행이어야 한다.
• 각 실험들은 두 가지 결과를 가진다. (보통 성공/실패 로 불린다.)
• 각 실험마다 한 결과에 대한 같은 확률을 지닌다. (e.g., P(sucess p) = 49%

Binominal coefficient

• P( 2 out of 5 newbons are girls) 를 구해야한다고 생각해보자,
• 우리는 이를 구하기 위해 5번의 newborns에 대해서 경우의 수를 세볼 수 있다. GBBBG, GGBBB, GBGBB, … 를 모두 세면 10개의 가능한 개수가 나온다.
• 이런 수를 모두 세기에는 n이 커질수록 급격하게 계산해야할 수가 늘어난다. 다행히 이는 일정한 패턴을 지녀 계수를 구해볼 수 있다.

• 이를 binominal coefficient 라고 부른다.

• ★★★ 이를 일반화하면 $P(k \; successes \; in \; experiments)$ = ${n! \over k!(n-k)!} p^k (1-p)^{n-k}$.

• 만약 10번의 게임을 해야한다고 해보자, 이 때 2번 준우승할 확률은? 각각 세 가지의 가능한 결과가 있다. P(우승) = 10% P(준우승) = 20% P(무승) = 70%.

• 10!/2!x8! (0.2)^2(0.8)^8 $\approx$ 0.3022

★★★Random variables

• 위 내용을 기반으로 ‘random variable’ 이라는 표현을 배워볼 것이다. 결론만 말하면, 위 30.2%의 확률은 P(X=2) = 30.2% 이렇게 쓸 수 있다.
• 우리가 10번의 실험을 할 때, 성공의 수는 랜덤하게 정해지게 된다. 어떤 집합은 10번의 시행에서 4번의 성공, 또 다른 집합은 7번의 성공을 얻었을 수 있다. 이 때, X는 “number of success” 로 지칭하며, 이 때의 X를 random variable이라고 부른다. 이 랜덤 변수는 일어날 확률과 함께 표현할 수 있고,

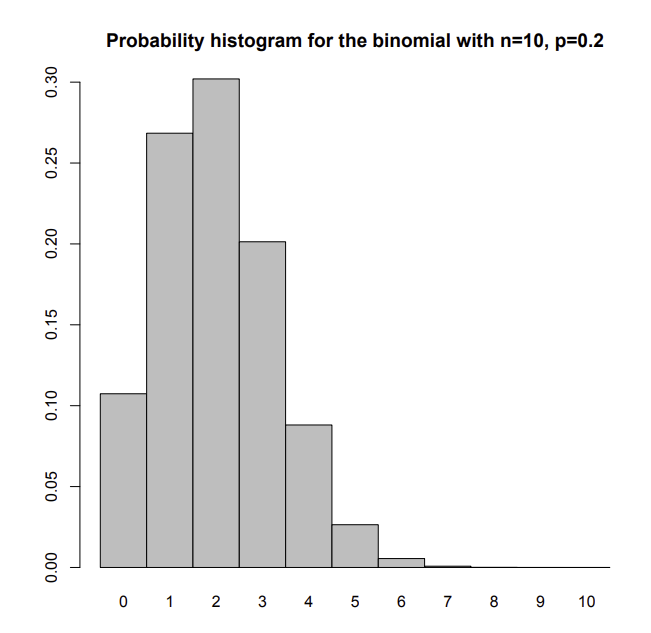
• 우리는 X=0, 1, …, 9, 10을 계산하여, 다음과 같이 확률 히스토그램으로 나타내볼 수 있다.
  • 물론 이 확률들은 실제 관측된 데이터들로 구성한 것이라기보단, 이론적으로 이상적인 형태라고 이해해야한다.
• 이 때, 세로는 데이터가 관측될 확률이라고 해석할 수 있다.

★★Normal approximation to the binomial

• 그럼 binomial 한 probability histogram에 대해서 normal approximation을 해보자.
• $n$의 크기를 계속 키워서 실험한다고 했을 때, binomial distribution은 점점더 normal한 curve 모양에 가까워진다.

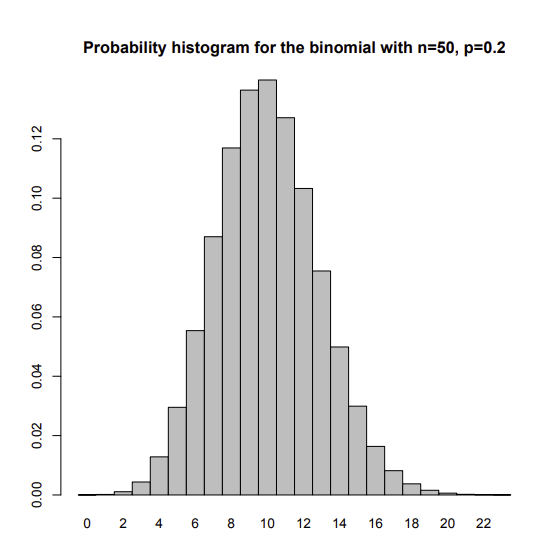
• 이 때, binominal probabilities를 normal approximate 하여서 빠르고! 간단하게 standardize하고 면적을 구해볼 수 있다.

• n은 시행 횟수, p는 랜덤변수 X=x에서의 확률이다. 이를 통해 $z$를 구할 수 있고, 위 소개한 정규분포 테이블을 통해 면적을 구할 수 있다.

• Exercise

1. A fair coin is tossed 400 times. Approximately what are the chances to get more than 210 tails? (Use the empirical rule and the normal approximation to the binomial distribution.)

   1) **16%** 2) 5% 3) 32%

• From the normal approximation to a binomial distribution for 400 trials and 1/2 probability of success, the mean number of successes is 400(1/2) = 200, and the standard deviation is the square root of 400(1/2)(1/2), which is 10.
  
• So 210 successes is one standard deviation above the mean. From the empirical rule, one half of 68% of the data lies within one standard deviation to the right of the mean, so 50 + (1/2)68 = 84% of the data lies to the left of 210. That is, 16% percent of the data lies to right of 210.