Week4 : Correlation Measures Linear Association
예측은 통계에서 아주 주요한 태스크 중 하나다. 예를 들어서 928명의 사람들 중 랜덤으로 한 명을 선택해서 키를 잰다고 했을 때, 평균은 그 사람의 키를 예측하는데 참고하기에 좋은 값이다.
여기에 그 사람의 아버지의 키에 대한 정보가 같이 주어진다고 생각해보자, 아버지의 키가 172cm 이상인 사람의 키를 예측한다고 했을 때, 더 나은 예측을 할 수 있게 도와줄 것이다. 바로 이런 작업들이 “regression” 이다.
The correlation coefficient
- Scatterplot은 두 quantative 한 variables의 관계를 시각화하기에 좋다.
- 방향을 표현할 수 있고, cluster의 모양을 확인할 수도 있으며, 점들 간에 얼마나 가까이, 멀리 있는지 확인을 통해 그 강도도 표현이 가능하다.
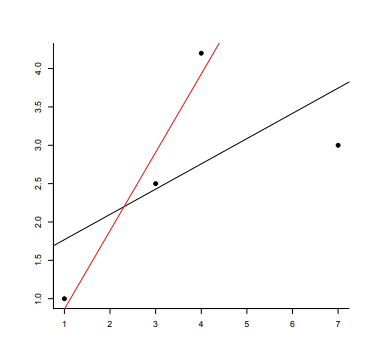
만약, 형태가 linear한 모양을 지닌다면, 그 강도를 correlation coefficient r 로 표현해볼 수 있다.
따라서 데이터 에 대해서, 아래와 같이 표현할 수 있다.
수식을 좀 더 해석해보면, X variable 정규화된 값과 Y variable의 정규화된 값을 곱한 것을 모두 합하여 그 샘플 개수만큼 나눠주면 correlation coefficient를 구할 수 있다.
Standardization 이라 생각하고 식을 단순화해보면, r = xy, y = 1/r x 로 그 관계에 대해서 표현하고 있음을 확인할 수 있다.

- 위 그림을 통해 scatter의 형태에 대해 정리해볼 수 있다.
- x축은 explanatory variable or predictor 세로축은 response variable 이라고 부른다.
- 이 때, 주의해야할 것이 linear한 형태에서 r이 의미를 갖고 유용하게 쓰일 수 있다. 그리고, correlation은 causation을 의미하지 않는다.
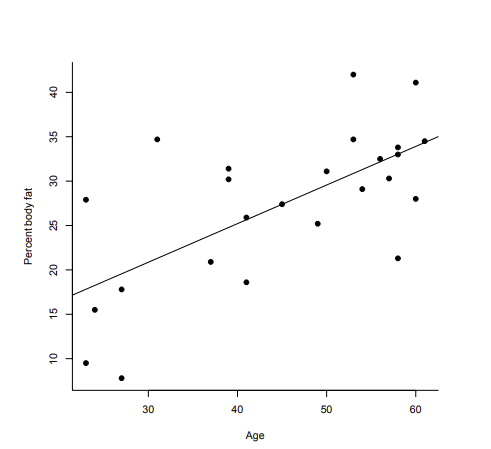
Regression line & Method of least squares
- Regression line 은 개의 pair 데이터 (x1, y1), …, (xn, yn) 에서 과 같은 equation을 찾는 작업이다. 이 line은 관찰된 와 의 유클리드 거리의 합을 최소화 하는 line을 선택하게 된다.
-
결국 regression의 가장 주요한 이용은 로부터 를 예측하는 데 있다.
-
위 equation을 구하기 위해서, 식을 세운다. 관측 데이터 와 우리가 세운 line 위의 와의 차이를 최소화하는 선을 유클리드 거리를 이용하면 위와 같이 식을 세울 수 있다.
-
이 때, 식을 대입하면, 으로 다시 쓸 수 있다**.
-
이 식으로부터 a와 b를 유도해보았다.
-
먼저 제곱을 날리고 시그마를 분배법칙에 의해서 다시 쓰면 으로 바꿀 수 있고 이 때, a는 i와는 상관없으므로 a로 다시 쓰면 로 구할 수 있다.
-
a 자리에 다시 위 식을 대입하여, 으로 쓸 수 있고, 는 동일한 형태이다 ( 로 대체). 로 표현해볼 수 있으므로 과 같은 꼴이 만들어져 로 수식을 유도해보았다.
Towards the mean
- “평균으로의 회귀” 는 골턴이 관찰한 현상으로 x가 s_x 만큼 더 좋을 때, y는 r x s_y 만큼 예측된다는 것이다. 보통 r의 범위는 -1 ~ 1 사이므로 이동이 더 작아진다고 볼 수 있다.
- 극단 케이스에서 주로 관찰되는 현상으로, 중간때 제일 좋은 점수를 받았던 사람의 경우 기말 때 원하는 수준보다 더 낮은 점수를 받거나, 중간 때 낮은 점수를 받은 그룹이 기말 때 올라가는 것이다. 다른 말로 regression effect, regression fallacy 라고도 부른다.
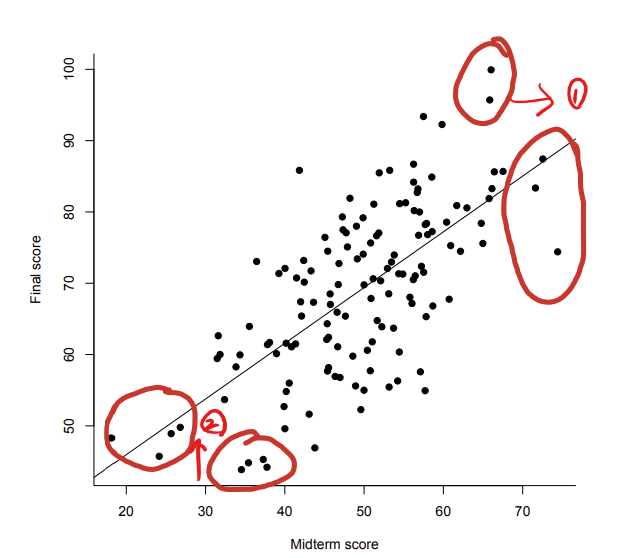
(흔히 위 scatter 형태를 “football shaped scatter” 라고 한다.)Example
- 예제를 통해 regression을 해보자. 관측 데이터의 = 49.5, = 69.1, =10.2, =11.8, =0.67 이라는 정보가 있다. 이 때, 중간고사에 41점 받은 사람의 기말고사 점수를 예측해보자. 를 구하기 위해, 위 식을 다시 정리해보면, 를 구하는 것으로 정리가능하다. 식을 다시 정리하면 를 구하면 된다. 49.5 - 41 / 10.2 0.83 = 69.1 - 0.67 x 0.83 x 11.8 = 62.5
- 위 정보를 토대로, 선형 회귀를 하면 41점을 받은 친구는 기말고사 때, 62.5을 받을 것이다.
Normal Approaximation in Regression
-
Linear regression 시, scatter는 football 모양을 필요로 한다. 이를 x 조건에서, y-value에 대해 normal approximation을 한다면 y-values에 대해서 더 많은 정보를 얻을 수 있다.
-
를 standardization 할 때, ★★★
로 나누어 를 구할 수 있다. -
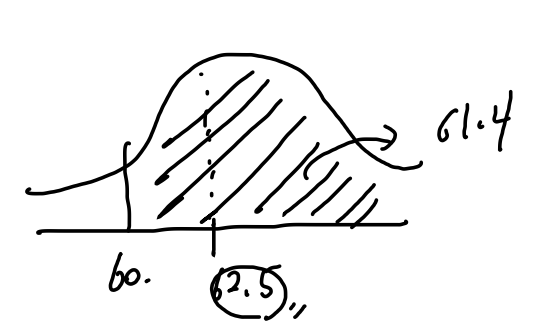
이를 이용하여, 위에서 제시되었던 정보를 바탕으로 중간고사에서 41점을 받은 학생이 기말에서 60 이상을 받을 확률은 어떻게 되는가? 라는 질문에 대해 계산해보자.
-
아까 계산에 의해, 기말고사 점수를 62.5로 예측해볼 수 있는데, 이를 standarize하면 62.5 - 60 / 11.8 X root(1-0.67^2) = -0.29
-
Normal Table에 의해, -0.29의 확률 밀도값을 확인가능하다. 즉, 61.4% 의 확률로 62.5의 점수를 받을 것이라고 예측해볼 수 있다.
Residual Plots
- 여기서 residual은 예측한 y-value들과 관찰된 값의 차이를 말한다.
- 이 residual 로 regression이 적합한지 이용해볼 수 있다.
아래와같이, curved한 pattern을 지닌 scatter도 data를 transforming하여 regression으로 분석해볼 수 있다.
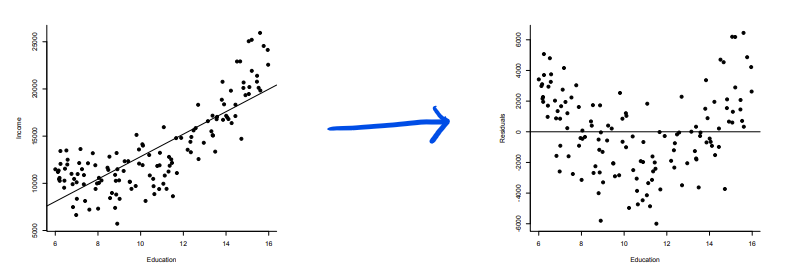
- 어떤 x-value가 x-values의 평균에서 멀리 떨어져있는 경우 high leverage를 갖는다고 표현하는데, 이는 regression line의 큰 변화를 가져올 가능성이 높다. 이 때, line의 변화를 influential point라고 하므로 high leverage로 인한 관찰 데이터가 많을수록 influential 하다고 표현할 수 있다.