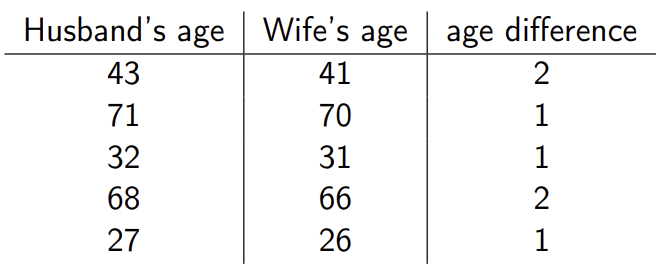[Introduction to Statistics] From Z-test to Sign test

Week5 : The logic behind testing hypotheses

Null hypothesis & Alternative hypothesis

$H_o$ (null hypothesis)

• Nothing extraordinary is going on

$H_A$ (alternative hypothesis)

• There is a different chance process that generates the data.

가설을 테스트하는 과정은 데이터를 수집하고 평가해서 데이터가 기존에 양립하는지 아닌지를 판단하는 과정이다. 만약, 양립하지 못한다면 $H_0$을 기각하게 된다.

이 때, 우리는 테스트를 하여 기각하고 싶은 가설을 $H_0$으로 둔다.

예를 들어, 동전을 던지는 실험을 10 번 실행한다고 했을 때, 7번의 tail이 나온 결과가 있다고 했을 때, 동전이 구부러지거나 편향되었다고 결정내리기 충분한 증거인가? 에 대해서 아래와 같이 표현하게 된다.

Test statistic & z-statistic

• Test statistic를 통해 데이터가 우리가 믿고 싶은 $H_0$이 사실이라는 것과 얼마나 떨어져있는지 측정한다. 보통, z-statistic를 이용한다.

• 실제 위 동전 뒤집기 사건으로 이를 계산해보자.
• “Observed”는 10번을 실행하였을 때, 실제 나온 tail의 수가 된다. → 7
• “Expected”는 $H_0$이 사실이라는 전제 하의 expected value를 구하게 된다.
  • E(sum) = 0 P(0) + 1P(1) = 1/2
  • = N * $\mu$ = 10x1/2 → 5
• “SE”는 마찬가지로 $H_0$이 사실이라는 전제 하에 랜덤 변수 X의 표준편차를 구한다. (Week 5, 샘플들에서 expected value, standard error를 구하는 방법을 배웠었다. $SE(S_n) = \sqrt n\sigma$ )
  • $\sigma$ = $\sqrt {np(1-p)}$
  • $\sqrt 10$ x $\sqrt {{1\over2} \times {1\over2}} \approx 1.58$
• 7-5 / 1.58 → 1.27

P-values & Statistically Significant

• $|z|$가 커질 수록 $H_0$가 기각될 증거가 더 커진다고 볼 수 있다.
• 이렇게 증거를 “The strength of the evidence”라고 표현하고, p-value 이를 표현한다.
• ★★★ p-value는 $H_0$가 true로 판단된다고 가정했을 때, $z$가 관찰된 $z$보다 더 높은 값을 갖게 될 확률이다.
• p-value가 작을수록, H0의 가설을 기각할 증거가 더 강력하다고 보면 된다. 보통 p-value가 5% 미만이면 H0을 기각한다 (statistically significant).
• (주의) p-value는 $H_0$이 사실인지 아닌지에 대해 정보를 주는 확률은 아니다. $H_0$를 사실이라고 가정했을 때, statistic의 확률을 검증하는 것이다.

예제를 들어서, Coke와 Pepsi를 구분하는 사건으로 $p \; value$를 계산해보자.

랜덤으로 10개의 컵에 coke와 pepsi가 채워져있다고 할 때, 둘의 차이가 있는지 없는지에 대해 임의의 사람들로 하여금 구분하도록 하여 수를 측정한다. 이 때, 사람들이 7개를 맞췄다면, Coke와 Pepsi가 구별 가능하다는 결론에 타당한 증거가 되는가?

먼저 z를 구하기 위해 이 사건에서 expected sum을 구해보면 위 동전과 같이 10x1/2→ 5가 된다. 관찰된 사건의 합인 7에서 5를 뺀 2를 마찬가지로 SE ($SE(S_n) = \sqrt n\sigma$ = 1.58)로 나눠주면, z value는 1.27이 나온다. 만약 H0이 사실이라면, z는 standard normal curve를 따른다고 볼 수 있고 중심극한 정리에 의해 p-value를 구해보면, 아래 그림과 같이 normal approximation해볼 수 있다.

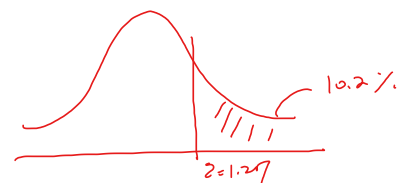
따라서, p-value를 percentage로 변환하면 10.2%가 되며 5%보다 작지 않으므로 $H_0$을 기각할 수 없다. 즉, 사람들이 coke, pepsi를 구분하지 못한다는 것을 기각하지 못한다.

T-test

• 위에서, SE of average를 구할 때, 기존 SE/n 을 하므로 아래와 같이 구할 수 있다. (Week 5: confidence interval를 참고하자.)

• $\sigma$가 안알려진 경우, Bootstrap principle을 이용해서 $\sigma$는 $s$로 추정할 수 있지만 $n$이 너무 작은 경우 ( $n \leq 20)$ normal curve는 z-statistic distribution을 사용하기에 좋은 approximation이 아니다.
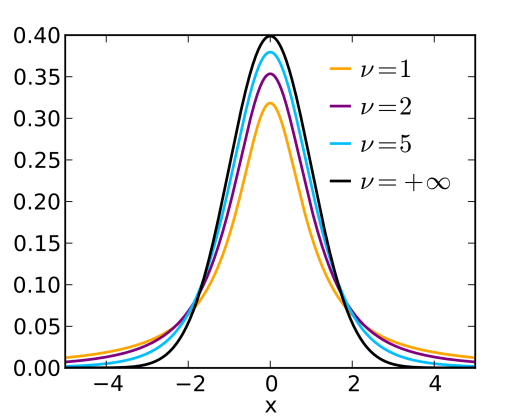
• ★★★이 때, student t-distribution을 n-1 의 자유도로 사용하여 approximation을 하게 된다.
• 위 그림에서 $v$는 자유도를 뜻하며, 자유도 $v$를 갖는 t 분포라고 부른다. t 분포에서 $v$가 높을 수록 0 중심에 몰리는 현상을 보여주며, 비교적 낮은 $v$에 대해서 몰리는 현상이 덜하다.
• 이는 낮은 표본에 대해서 신뢰도가 낮아지는 부분을 고려하여, 예측 범위를 넓히기 위함이다.

기타

Two-sample z-test

• 두 샘플에 대해서도 z-test를 할 수 있다.
• 예를 들어, 저번달에 1000개의 샘플링한 것을 통해 대통령 지지율을 55%를 측정하고 이번 달 1500개의 샘플을 통해 58%를 얻었다고 해보자. 이런 사실에 대해 지지율에 변화가 있는지를 검증하고 싶다. 따라서, 우리는 $H_0$의 경우 지지율에 변화가 없다. 를 놓고 기각하기 위한 검증을 실시하려고 한다.
• 이 때, $H_0 : p_2 - p_1 = 0$ ; $H_1 : p_2 - p_1 \ne 0$ 으로 둘 수 있다.
• z-test를 계산 하면, z = observed diff - expected diff / SE of diff

• 위처럼 쓸 수 있고 $SE(\hat p_1)$는 $\sigma / \sqrt n$ 이며, central limit theorem 을 적용했을 때, $\sigma = p(1-p)$ 으로 쓸 수 있다. 따라서, 계산하면 0.03 / root((0.55 0.45)/1000 + (0.580.42)/1500) $\approx$ 0.0202 → 1.485

Sign Test

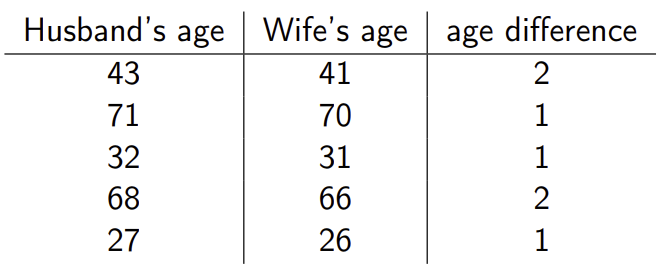
• Matched pairs : 다음 아래 자료를 볼 때, 남편의 나이와 아내의 나이는 완전히 독립적이라곤 볼 수 없다.
• matched pairs에 대해서 paired t-test를 수행 가능하다. 각 차이 $d_i$의 평균 $\bar d$를 이용하며, 분산도 이 차이의 분산을 이용하여 구한다 ($\sigma_d/\sqrt n)$.