문제
https://www.acmicpc.net/problem/10844
45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.
입력
첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
풀이
길이가 5인 계단 수를 예로 들어 생각해보자. 1로 시작하는 계단수, 2로 시작하는 계단수, 3으로 시작하는 계단수, ... , 9로 시작하는 계단수로 나눌 수 있다. 9가지 경우를 모두 더하면 정답을 구할 수 있다. 길이가 5인 계단 수를 구하기 위해 길이가 1인 계단수부터 생각해보자. 1로 시작하며, 길이가 1인 계단수는 1이다. 마찬가지로 2~9로 시작하며 길이가 1인 계단수는 1이다. 차례대로 길이를 늘려가며 계단수를 구해보면 일정한 규칙을 찾을 수 있다. 길이가 5인 계단수를 구하려면 길이가 1, 2, 3, 4인 계단수를 차례대로 구해내며 찾을 수 있다.
행은 수의 길이(1~N), 열은 시작하는 수(0~9)로 이루어진 2차원 dp 배열을 생성한다.

0으로 시작하는 계단수는 없지만 동적계획법으로 문제를 풀기 위해 필요하다. 마지막에 계단수를 합할 때 column 값이 1~9인 항목만 더하여 구해주면 된다.
dp 배열을 구할 때 규칙은 다음과 같다.
- 길이가 1인 계단수는 1이다.
- 0으로 시작하는 계단수는 직전 행의 index 1 값과 같다.
- 9로 시작하는 계단수는 직전 행의 index 8 값과 같다.
- 2, 3의 경우를 제외한 내부에 있는 계단수는 직전 행의 index-1과 index+1을 더해준 값과 같다.
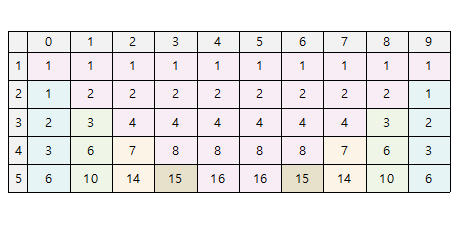
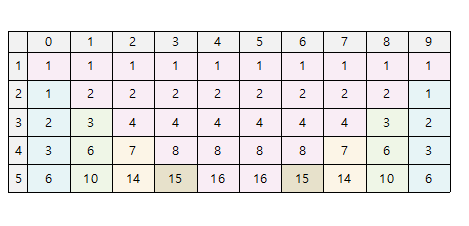
이를 토대로 길이가 5인 계단수를 구하기 위한 동적 배열 dp에 저장될 값을 표로 나타내면 다음과 같다. 위에 언급한 바와 같이 0으로 시작하는 계단수부터 구해야 하며, 길이가 1인 계단수부터 5인 계단수까지 차례대로 구해준다.
위에서 만든 규칙을 토대로 식을 작성해보면 다음과 같다.
// 1번 규칙 - 길이가 1인 계단수는 1이다.
for (int i = 0; i < 10; i++) {
dp[1][i] = 1;
}
for (int i = 2; i <= N; i++) {
for (int j = 0; j < 10; j++) {
// 2번 규칙 - 0으로 시작하는 계단수는 직전 행의 index1 값과 같다.
if (j == 0) dp[i][j] = dp[i - 1][1];
// 3번 규칙 - 9로 시작하는 계단수는 직전 행의 index8 값과 같다.
else if (j == 9) dp[i][j] = dp[i - 1][8];
// 4번 규칙 - 직전 행의 index-1과 index+1을 더해준 값과 같다.
else dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]);
}
}dp 배열을 long 타입으로 선언하고 1,000,000,000으로 나누어주는 부분만 조심하면 문제를 해결할 수 있다.
전체 코드
import java.io.*;
import java.util.*;
class Main {
public static long[][] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
bw.write(String.valueOf(dfs(N)) + "\n");
bw.flush();
bw.close();
}
public static long dfs(int N) {
dp = new long[N + 1][10];
for (int i = 0; i < 10; i++) {
dp[1][i] = 1;
}
for (int i = 2; i <= N; i++) {
for (int j = 0; j < 10; j++) {
if (j == 0) dp[i][j] = dp[i - 1][1];
else if (j == 9) dp[i][j] = dp[i - 1][8];
else dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]) % 1000000000;
}
}
long sum = 0;
for (int i = 1; i < 10; i++) {
sum += dp[N][i];
sum %= 1000000000;
}
return sum % 1000000000;
}
}실수 모음
처음에 1,000,000,000으로 나눠줘야 하는 부분을 다음과 같이 작성했다.
sum += dp[N][i] % 1000000000이렇게 작성하면 누적합인 sum 변수의 값을 매번 1,000,000,000으로 나눠주는 게 아니라 dp 배열의 값을 나눈 후에 sum 변수에 더해진다. dp 배열에 저장될 때 이미 연산이 되어 있으며 추가적으로 sum 변수에 값을 더해가며 누적할 때 한 번 더 1,000,000,000으로 나누어줘야 올바르게 구할 수 있다.
또한 sum 변수만 long 타입으로 선언하는 것이 아니라 dp 배열도 long 타입 배열로 선언해야 한다. 이미 각 계단수들이 int 타입의 범위를 벗어나기 때문이다.
