[프로그래머스] 등굣길 (동적계획법 Lv. 3) - 자바 Java

문제

https://school.programmers.co.kr/learn/courses/30/lessons/42898

계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.

아래 그림은 m = 4, n = 3 인 경우입니다.

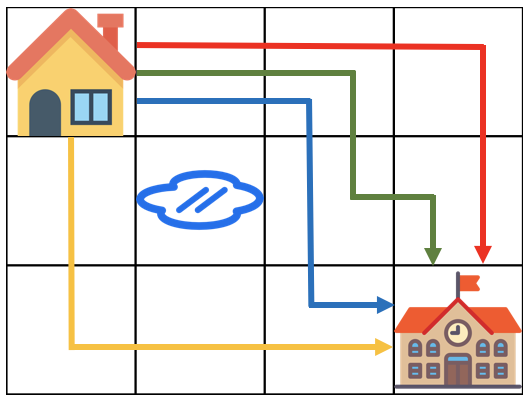
가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.

격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.

제한사항

• 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
• m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다.
• 물에 잠긴 지역은 0개 이상 10개 이하입니다.
• 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.

풀이

m이 가로 길이, n이 세로 길이라서 2차원 배열을 만들 때 행과 열이 조금 헷갈리지만 무시하고 풀어도 문제가 없다. 어차피 주어지는 puddles 배열도 열, 행 순서대로 주어지기 때문에 굳이 m과 n의 순서를 바꾸어 2차원 배열을 생성할 필요는 없다.

동적 계획법으로 풀이하기 위해 2차원 dp 배열을 생성한다. 이때 좌표의 크기를 하나씩 크게 설정해서 문제에 제시된 것처럼 집의 좌표가 (1, 1), 학교의 좌표가 (m, n)이 될 수 있도록 한다. puddles 배열도 (1, 1)로 시작하는 것을 전제로 주어지기 때문에 이렇게 푸는 것이 한결 더 편하다.

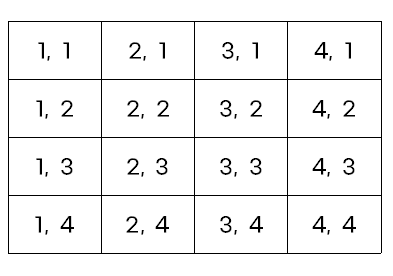
int dp[][] = new int[m + 1][n + 1];

장애물이 있는 부분은 지나갈 수 없기 때문에 dp 배열의 해당 좌표에 -1을 저장한다.

for (int i = 0; i < puddles.length; i++) {
            dp[puddles[i][0]][puddles[i][1]] = -1;
}     

이 문제의 problem은 집에서 학교까지 가는 최단경로의 개수이고, 집에서 각 좌표까지의 최단경로의 개수를 sub problem으로 둘 수 있다.

집에서 집까지 가는 최단 경로의 개수는 1가지이므로 dp[1, 1]에 1을 저장한다. 집에서 직선 거리에 있는 집들까지의 최단 경로의 개수도 마찬가지로 1이다.

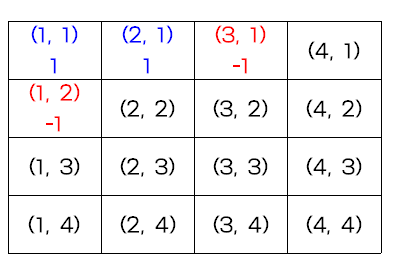
단, 이 경우 아래와 같이 장애물을 만나면 더이상 갈 수 있는 방법이 없다. 오른쪽과 아래쪽으로만 움직일 수 있기 때문이다.

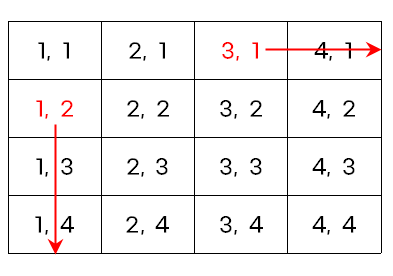
위와 같이 집과 직선 거리에 있는 경로에 장애물이 있는 경우 해당 지점부터 끝까지 갈 수 없는 위치라고 판단하며 -1을 저장한다.

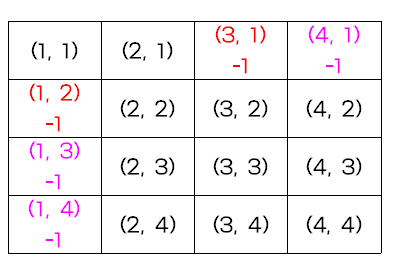
이를 코드로 나타내면 다음과 같다.

for (int i = 2; i <= m; i++) {
	// 장애물이 있는 칸이 아니라면 직전 dp 배열의 값과 같다.
	if (dp[i][1] != -1) {
    	dp[i][1] = dp[i - 1][1];
    } else {
    //장애물이 있는 칸이라면 지금 위치부터 직선 끝까지 dp 배열에 -1을 저장한다.
    	for (int j = i; j <= m; j++)\
        	dp[j][1] = -1;
            break;
		}
}


for (int i = 2; i <= n; i++) {
	if (dp[1][i] != -1) {
    	dp[1][i] = dp[1][i - 1];
    } else {
    	for (int j = i; j <= n; j++)
        	dp[1][j] = -1;
            break;
	}
}

초기값 설정을 완료하면 왼쪽과 위쪽 두 곳에서부터 올 수 있는 위치만 남는다. 이 경우 최단경로의 개수는 왼쪽 dp와 위쪽 dp의 값을 더해주면 구할 수 있다. 이때 왼쪽 dp와 위쪽 dp가 모두 -1이라면 현재 위치에 올 수 없다는 뜻이므로 -1을 저장한다. 만약 왼쪽 dp나 위쪽 dp 중 어느 한쪽의 값이 -1이라면 다른쪽 dp의 값을 그대로 저장한다. 이를 토대로 다음과 같이 구할 수 있다.

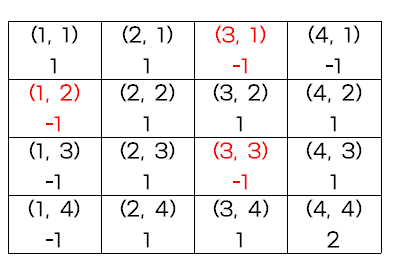
전체 코드

class Solution {


    public int solution(int m, int n, int[][] puddles) {
        int MOD = 1000000007;

        int dp[][] = new int[m + 1][n + 1];


        for (int i = 0; i < puddles.length; i++) {
            dp[puddles[i][0]][puddles[i][1]] = -1;
        }

        dp[1][1] = 1;

        for (int i = 2; i <= m; i++) {
            if (dp[i][1] != -1) {
                dp[i][1] = dp[i - 1][1];
            } else {
                for (int j = i; j <= m; j++)
                    dp[j][1] = -1;
                break;
            }

        }


        for (int i = 2; i <= n; i++) {
            if (dp[1][i] != -1) {
                dp[1][i] = dp[1][i - 1];
            } else {
                for (int j = i; j <= n; j++)
                    dp[1][j] = -1;
                break;


            }
        }

        for (int i = 2; i <= m; i++) {
            for (int j = 2; j <= n; j++) {

                if (dp[i][j] == -1) continue;
                else if (dp[i - 1][j] == -1 && dp[i][j - 1] == -1) dp[i][j] = -1;
                else if (dp[i - 1][j] == -1) dp[i][j] = dp[i][j - 1];
                else if (dp[i][j - 1] == -1) dp[i][j] = dp[i - 1][j];
                else dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % MOD;
            }
        }

        if (dp[m][n] == -1) return 0;

        return dp[m][n] % MOD;
    }

}

실수 모음

• 나누기 연산을 하지 않았다.
• 학교까지 갈 수 없는 케이스가 테스트케이스에 있었다. dp 배열에서 장애물이 있거나 다다를 수 없는 곳은 최종적으로 -1이 저장되는데, 0이 출력되어야 한다. 그래서 반환하기 전 마지막 줄에 return dp[m][n] % MOD;를 추가했다.