[WEEK01] 백준 1914 하노이 탑

문제

세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 100)이 주어진다.

출력

첫째 줄에 옮긴 횟수 K를 출력한다.

N이 20 이하인 입력에 대해서는 두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다. N이 20보다 큰 경우에는 과정은 출력할 필요가 없다.

풀이

재귀함수 문제라고 한다.
일단 어떻게 시작해야할지 몰라 단계별로 그려보았다.

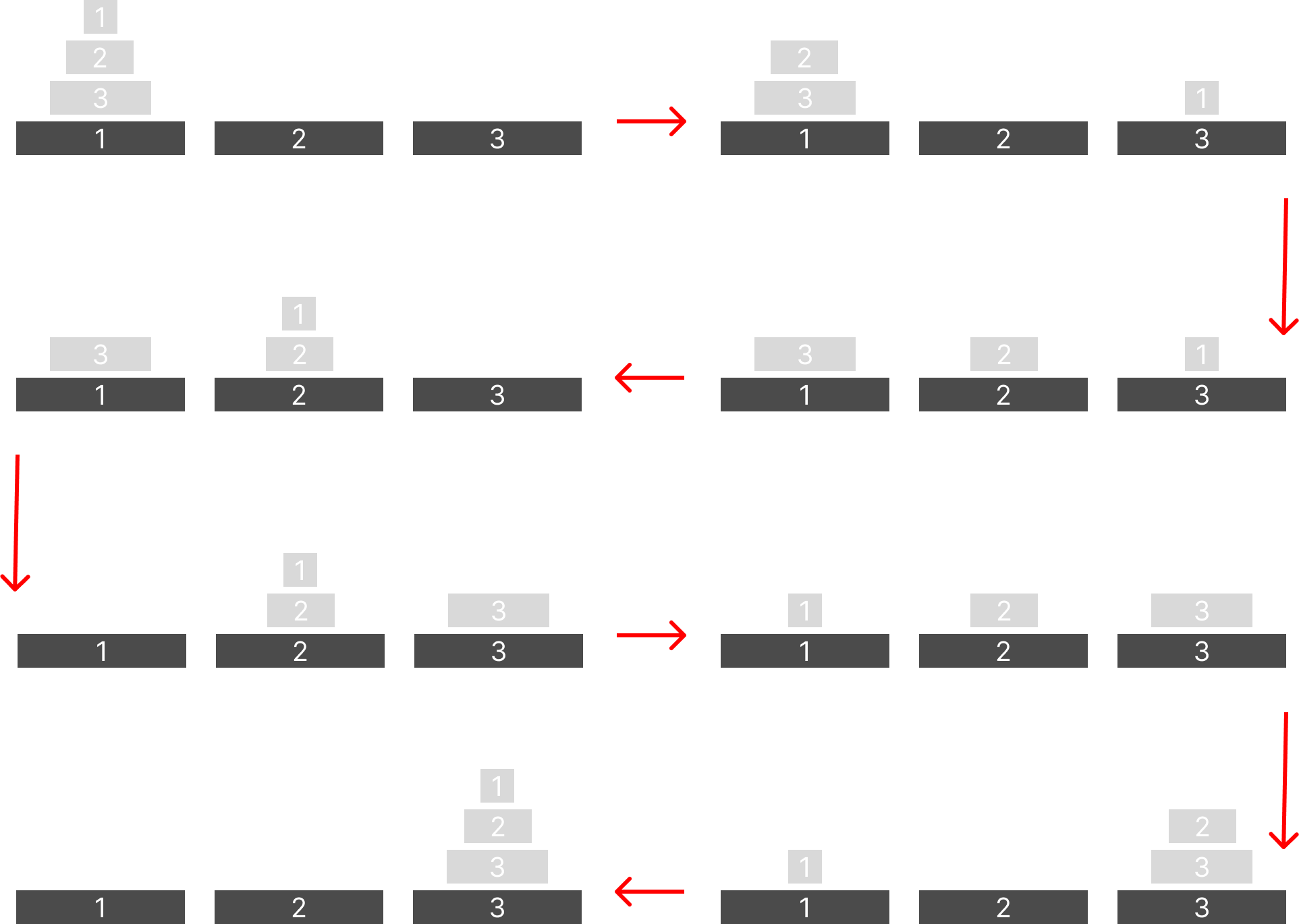
특정 단계만 살펴보겠다.

start: 1 via: 2 end: 3

• 첫번째 -> 두번째
  2개 짜리를 1 -> 2
• 두번째 -> 세번째
  3번 블럭을 1 -> 3
• 세번째 -> 네번째
  2개 짜리를 2 -> 3
  

def hanoi(n, start, end, via):
	if n == 0:
    	return
    hanoi(n-1, start, via, end)
    print(start, end)
    hanoi(n-1, via, end, start)

전체코드

def hanoi(n, start, end, via):
    if n==0:
        return
    hanoi(n-1, start, via, end)
    print(start, end)
    hanoi(n-1, via, end, start)


n = int(input())
count = 2**n - 1

if n > 20:
    print(count)
else:
    print(count)
    hanoi(n, 1, 3, 2)