[WEEK02] 백준 13334 철로

문제

집과 사무실을 통근하는 n명의 사람들이 있다. 각 사람의 집과 사무실은 수평선 상에 있는 서로 다른 점에 위치하고 있다. 임의의 두 사람 A, B에 대하여, A의 집 혹은 사무실의 위치가 B의 집 혹은 사무실의 위치와 같을 수 있다. 통근을 하는 사람들의 편의를 위하여 일직선 상의 어떤 두 점을 잇는 철로를 건설하여, 기차를 운행하려고 한다. 제한된 예산 때문에, 철로의 길이는 d로 정해져 있다. 집과 사무실의 위치 모두 철로 선분에 포함되는 사람들의 수가 최대가 되도록, 철로 선분을 정하고자 한다.

양의 정수 d와 n 개의 정수쌍, (hi, oi), 1 ≤ i ≤ n,이 주어져 있다. 여기서 hi와 oi는 사람 i의 집과 사무실의 위치이다. 길이 d의 모든 선분 L에 대하여, 집과 사무실의 위치가 모두 L에 포함되는 사람들의 최대 수를 구하는 프로그램을 작성하시오.

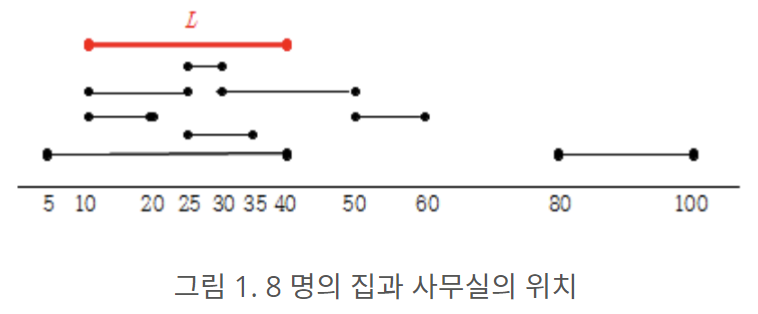
그림 1. 8 명의 집과 사무실의 위치

그림 1 에 있는 예를 고려해보자. 여기서 n = 8, (h1, o1) = (5, 40), (h2, o2) = (35, 25), (h3, o3) = (10, 20), (h4, o4) = (10, 25), (h5, o5) = (30, 50), (h6, o6) = (50, 60), (h7, o7) = (30, 25), (h8, o8) = (80, 100)이고, d = 30이다. 이 예에서, 위치 10 과 40 사이의 빨간색 선분 L이, 가장 많은 사람들에 대하여 집과 사무실 위치 모두 포함되는 선분 중 하나이다. 따라서 답은 4 이다.

입력

입력은 표준입력을 사용한다. 첫 번째 줄에 사람 수를 나타내는 양의 정수 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 각 줄에 정수 쌍 (hi, oi)가 주어진다. 여기서 hi와 oi는 −100,000,000이상, 100,000,000이하의 서로 다른 정수이다. 마지막 줄에, 철로의 길이를 나타내는 정수 d (1 ≤ d ≤ 200,000,000)가 주어진다.

출력

출력은 표준출력을 사용한다. 길이 d의 임의의 선분에 대하여, 집과 사무실 위치가 모두 그 선분에 포함되는 사람들의 최대 수를 한 줄에 출력한다.

풀이

(집 사무실), (사무실 집) 순서는 중요치 않다. 따라서 입력받은 좌표값은 (작은좌표, 큰좌표) 로 배열에 저장을 하고, 이 배열을 끝점 기준으로 오름차순 정렬을 해준다.
또 거리가 d보다 큰 좌표는 빼준다.

이제 끝점을 1개씩 읽어오면서 끝점 기준 왼쪽으로 철로를 d만큼 깔아본다.
철로를 깐 현재점은 당연히 포함될것이고, 힙에 넣어준다.

2번째 끝점 에서 왼쪽으로 d만큼 깔아준다. 힙에 들어있는 좌표가 철로에 포함되지 않는다면 빼준다.

이 과정을 반복해준다.

최소힙을 사용하게 되는데 이유는 끝점이 같은 좌표가 있다고 하면, 철로로부터 멀리 떨어진것부터 판단하기 위해서이다.

전체코드 1

import sys
import heapq

coordis = []            # 좌표들 저장
valid_coordis = []      # 실제 철로 길이와 비교할 좌표들 
heap = []
d = 0                   # 철로 길이
result = 0              # 최대 수

# 좌표 입력
for _ in range(int(input())):
    tmp = list(map(int, sys.stdin.readline().split()))
    coordis.append(sorted(tmp))

print(coordis)
# 철로 길이 입력
d = int(input())

# 두 점 사이의 길이가 d 이하인 좌표만 넣어줌
for coordi in coordis:
    if abs(coordi[0] - coordi[1]) > d: continue
    valid_coordis.append(coordi)

print(valid_coordis)

# 끝점 기준으로 오름차순
valid_coordis = sorted(valid_coordis, key = lambda x: x[1])
print(valid_coordis)

for coordi in valid_coordis:

    # 없으면 넣어줌
    if not heap:
        heapq.heappush(heap, coordi)
        continue

    # 안에 있던 시작점이 현재 끝점에서 d만큼 뺀것보다 작다면 범위 안에 없으니 제거
    # 시작점이 작은거부터 제거해야 원하는대로 동작 -> 항상 최소힙 상태면 가능
    while heap[0][0] < coordi[1] - d:
        # 시작점 작은거 날림
        heapq.heappop(heap)
        # 날리고 비어있으면 종료
        if not heap:
            break

    # 제거할게 없으면 현재 좌표 넣어줌    
    heapq.heappush(heap, coordi)
    # 최대 수 갱신
    result = max(result, len(heap))

print(result)

만약에 철로를 시작점에서부터 깐다면 처음에 끝점 기준으로 정렬을 하게 되고 최대힙을 사용하게 된다.
밑의 코드는 위와 달리 시작점 기준으로 철로를 깔았을 때이다.

전체코드 2

import sys
import heapq

n = int(input())
tmp_start_end_pos = []
start_end_pos = []
heap = []
result = 0

# 시작점 끝점을 정렬해서 넣어줌
for _ in range(n):
    h, o = map(int, sys.stdin.readline().split())
    tmp_start_end_pos.append(sorted([h, o]))

d = int(input())

# 시작점 끝점 거리가 d 이하인 것들을 새 배열에 넣어줌
for i in range(n):
    if abs(tmp_start_end_pos[i][0] - tmp_start_end_pos[i][1]) > d: continue
    start_end_pos.append(tmp_start_end_pos[i])

# 시작점 기준으로 내림차순
start_end_pos = sorted(start_end_pos, key = lambda x: -x[0])

for start, end in start_end_pos:
    # 범위 밖에 있으면 빼주고
    while heap and start + d < -heap[0]:
        heapq.heappop(heap)

    # 끝점 정보만 최대힙으로 넣어줌
    # 시작점부터 철로를 두니 끝점이 멀리있는것부터 비교해줘야 함
    heapq.heappush(heap, -end)
    result = max(result, len(heap))

print(result)