문제
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자모양 상자의 칸에 하나씩 넣은 다음, 상자들을 수직으로 쌓아 올려서 창고에 보관한다.
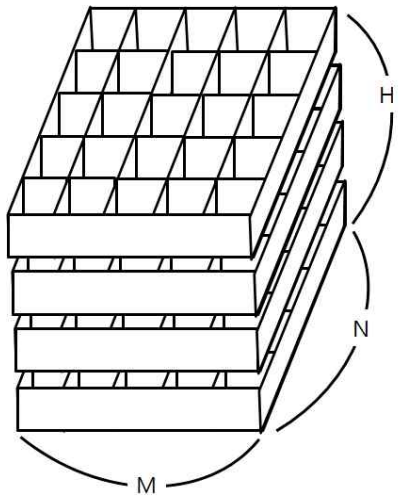
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토에 인접한 곳은 위, 아래, 왼쪽, 오른쪽, 앞, 뒤 여섯 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지 그 최소 일수를 알고 싶어 한다.
토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.
입력
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100, 1 ≤ H ≤ 100 이다. 둘째 줄부터는 가장 밑의 상자부터 가장 위의 상자까지에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 하나의 상자에 담긴 토마토의 정보가 주어진다. 각 줄에는 상자 가로줄에 들어있는 토마토들의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0 은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다. 이러한 N개의 줄이 H번 반복하여 주어진다.
토마토가 하나 이상 있는 경우만 입력으로 주어진다.
출력
여러분은 토마토가 모두 익을 때까지 최소 며칠이 걸리는지를 계산해서 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.
풀이
처음에는 백준 2573 빙산문제와 같은 방식으로 풀려고했다.
완숙토마토 좌표를 저장해놓고 해당 좌표 주변에 반숙토마토가 몇개 있나를 저장하고 탐색이 끝났을 때 반숙토마토가 존재했다면 완숙토마토 주변에 있던 반숙토마토를 익혀주는 식으로 반복을 하다가 더이상 반숙토마토를 발견하지 못하면 답을 출력하려 했다.
하지만 이렇게 하려니 익힐 반숙토마토가 아예 없는 경우와 해당 반숙토마토에 접근할 수 없는 경우에 둘 다 완숙토마토 기준으로 주변에 반숙토마토의 개수는 0으로 나오게되고 구분하기가 힘들어진다. 또 시간도 굉장히 오래걸려서 접근 방법을 다르게하였다.
탐색 -> 익히기 -> 탐색 -> 익히기 방식이 아닌
한번의 탐색으로 익힐 수 있는 토마토를 전부 익혔다.
완숙토마토 위치의 값이 1이라면 breadth가 퍼져나가면서 1씩 더해주면서 익혔다. 최종적으로 그래프의 값중 가장 큰값을 읽어오고 -1 해준 값을 출력해주면 걸린 일수가 나온다.
전체코드
import sys
from collections import deque
input = sys.stdin.readline
def bfs():
while q:
z, x, y = q.popleft()
for dz, dx, dy in direction:
nz, nx, ny = z + dz, x + dx, y + dy
if nz < 0 or nz > h - 1 or nx < 0 or nx > n - 1 or ny < 0 or ny > m - 1:
continue
# 현재 익는 토마토가 있는 위치의 값은
# day + 1 이다
if not visit[nz][nx][ny] and graph[nz][nx][ny] == 0:
graph[nz][nx][ny] = graph[z][x][y] + 1
visit[nz][nx][ny] = 1
q.append((nz, nx, ny))
m, n, h = map(int, input().split())
graph = [[] for _ in range(h)]
visit = [[[0] * m for _ in range(n)] for _ in range(h)]
direction = [(0, -1, 0), (0, 0, -1), (0, 1, 0), (0, 0, 1), (1, 0, 0), (-1, 0, 0)]
day = 0
q = deque()
for i in range(h):
for j in range(n):
graph[i].append(list(map(int, input().split())))
# 1인 지점을 먼저 다 집어넣고 bfs를 돌려야 함
# 안 그러면 양쪽에 1이 있다 가정할 때 가운데로 좁혀오면 3일이면 될걸
# 한쪽에서만 먼저 bfs를 진행해주면 6일이 걸리기 때문
for k in range(h):
for i in range(n):
for j in range(m):
if not visit[k][i][j] and graph[k][i][j] == 1:
visit[k][i][j] = 1
q.append((k, i, j))
bfs()
# 3중 for문 어떻게 탈출할지 몰라서 죄다 break 걸어줌
for k in range(h):
for i in range(n):
for j in range(m):
# 익힐 수 있는건 다 익혔는데 0이 남아있다면 -1
if graph[k][i][j] == 0:
day = -1
break
# graph 인덱스중 가장 큰거 - 1 이 답임
day = max(day, graph[k][i][j] - 1)
if day == -1:
break
if day == -1:
break
print(day)