#1: 모든 노드는 red or black
#2: 루트 노드는 black
#3: 모든 nil 노드는 black
#4: red의 자녀들은 black
#5: 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다
삽입
RBTree의 경우 이진트리처럼 새로운 노드를 삽입하고나서 룰을 위반했다면 추가적인 조정을 해주는 방식이다.
새롭게 삽입되는 노드의 색깔을 RED로 #2, #4를 위반할 가능성이 생긴다. 따라서 #2, #4를 위반했을 때 각각이 경우에 따라 적절한 조치를 해준다.
#2를 위반했을 때에는 간단하다. 새롭게 삽입된 노드를 BLACK으로 바꿔주면 된다.
#4를 위반했을 때에는 3가지 경우로 나누어 각각에 맞춰 해결한다.
방법은 아래와 같다.
case. 3
부모의 형제가 BLACK이고, 뻗은 형태로 있을 때
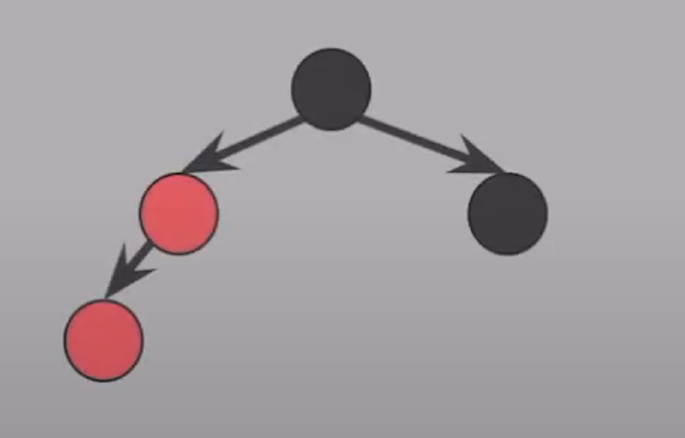
- 부모와 할아버지 색을 바꾼다.
- 할아버지 기준 오른쪽 회전한다.
case. 2
부모의 형제가 BLACK이고, 꺾인 형태로 있을 때
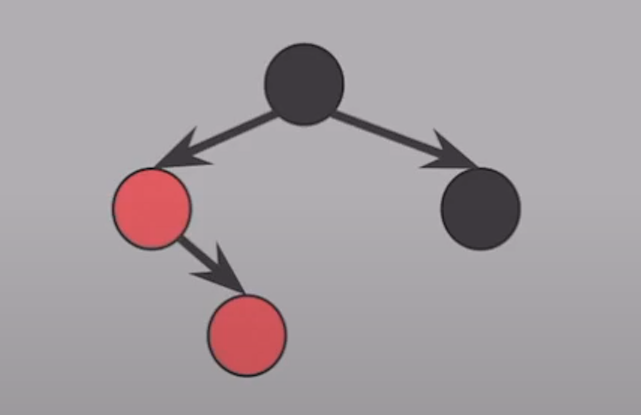
- 부모 기준 왼쪽 회전한다.
- case. 3과 동일하게 해결한다.
case. 1
부모의 형제가 RED일 때
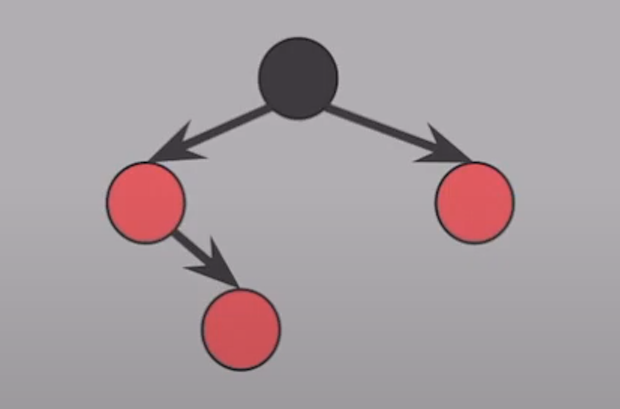
- 부모와 부모형제의 RED를 한데모아 할아버지에게 넘겨준다.
- 할아버지 기준으로 다시 #4를 위반하는지 확인한다.
[삽입 예제 링크]
https://youtu.be/2MdsebfJOyM?t=1490
코드
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *p = t->nil;
node_t *now = t->root;
// 입력받은 key를 가지는 node 생성
node_t *node = (node_t *)calloc(1, sizeof(node_t));
node->key = key;
// key 값이 들어갈 적절한 빈 공간을 찾기
while (now != t->nil){
// 적절한 위치를 찾았을 때 해당위치의 부모를 알기 위해 캐싱
p = now;
if (node->key < now->key)
now = now->left;
else
now = now->right;
}
// 새 node에 부모 연결
node->parent = p;
// 부모가 nil node였으면 처음부터 root가 비어있었다는 것
// 새 node를 root node로 지정
if (p == t->nil)
t->root = node;
// 부모에 새 node 연결
else if (node->key < p->key)
p->left = node;
else
p->right = node;
// 새 node의 left, right를 nil node로 초기화
// 새로 삽입되는 node는 무조건 RED
node->left = t->nil;
node->right = t->nil;
node->color = RBTREE_RED;
// 이진 트리 방식으로 삽입이 끝났으면
// RBTree의 룰을 위반하지 않았는지 검사
rbtree_insert_fixup(t, node);
return node;
}위의 코드는 이진트리의 삽입 방식과 거의 유사하다.
root가 비어있었다면 새롭게 생성되는 노드를 root로 지정을 하고,
비어있지 않았으면 새 노드가 들어갈 적절한 위치를 찾고 해당 위치의 부모를 새 노드의 parent가 가르키게 한다.
새로 삽입되는 노드의 색깔은 RED이다. 따라서 #2와 #4를 위반하지 않는지 검사를 해야한다. 검사 진행 중 위반을 하였다면 위에 소개하였던 case 1, 2, 3에 따라 해결해야한다.
이러한 동작을 맡는 함수가 rbtree_insert_fixup이다. 코드는 아래와 같다.
void rbtree_insert_fixup(rbtree *t, node_t *node) {
// 새로 추가된 노드가 root 노드라면 BLACK으로 바꿔주고 종료
// #2를 위반했을 때
if (node == t->root) {
node->color = RBTREE_BLACK;
return;
}
// 추가된 노드의 부모가 같은색이라면 -> RED가 연속으로 나타나면
// #4를 위반하지 않을 때까지 무한반복
while (node->parent->color == RBTREE_RED) {
// 할아버지 기준 왼쪽에 있을 때
if (node->parent == node->parent->parent->left) {
// 부모형제의 색깔이 RED일 때 -> case.1
if (node->parent->parent->right->color == RBTREE_RED) {
// 부모와 부모형제의 RED를 모아 위로 올려줌
node->parent->color = RBTREE_BLACK;
node->parent->parent->right->color = RBTREE_BLACK;
// 할아버지는 RED를 받음
node->parent->parent->color = RBTREE_RED;
// 할아버지가 새로운 RED가 되었으니 #4를 위반하는지 검사
node = node->parent->parent;
}
else { // 부모형제의 색깔이 BLACK일 때
// 왼쪽 영역에 있는데 부모의 오른쪽일 때 -> 꺾인 형태 -> case.2
// case.2는 case.3으로 바꿔주고 case.3과 동시에 처리
if (node == node->parent->right) {
node = node->parent;
rbtree_left_rotate(t, node);
}
// 왼쪽 영역에 있는데 부모의 왼쪽일 때 -> 뻗은 형태 -> case.3
node->parent->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
rbtree_right_rotate(t, node->parent->parent);
}
}
// 할아버지 기준 오른쪽에 있을 때
// 왼쪽과 대칭이니 똑같은 방식으로 해주면 됨
else {
if (node->parent->parent->left->color == RBTREE_RED) {
node->parent->color = RBTREE_BLACK;
node->parent->parent->left->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
node = node->parent->parent;
}
else {
if (node == node->parent->left) {
node = node->parent;
rbtree_right_rotate(t, node);
}
node->parent->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
rbtree_left_rotate(t, node->parent->parent);
}
}
}
}rotate 함수의 코드는 아래와 같다.
void rbtree_left_rotate(rbtree *t, node_t *node) {
node_t *tmp = node->right;
// node와 tmp->left 상호연결
node->right = tmp->left;
if (tmp->left != t->nil)
tmp->left->parent = node;
// tmp와 node->parent 상호연결
tmp->parent = node->parent;
if (node->parent == t->nil)
t->root = tmp;
else if (node == node->parent->left)
node->parent->left = tmp;
else
node->parent->right = tmp;
// tmp와 node 상호연결
tmp->left = node;
node->parent = tmp;
}
void rbtree_right_rotate(rbtree *t, node_t *node) {
node_t *tmp = node->left;
// node와 tmp->right 상호연결
node->left = tmp->right;
if (tmp->right != t->nil)
tmp->right->parent = node;
// tmp와 node->parent 상호연결
tmp->parent = node->parent;
if (node->parent == t->nil)
t->root = tmp;
else if (node == node->parent->left)
node->parent->left = tmp;
else
node->parent->right = tmp;
// tmp와 node 상호연결
tmp->right = node;
node->parent = tmp;
}삭제
삭제를 할 때에는 삭제된 노드의 색깔에 따라 #2, #4, #5를 위반할 가능성이 있다. 따라서 삭제된 노드의 색깔이 중요하다
red 노드가 삭제가 된다면 5가지 조건을 위반할리 없다.
즉, black 노드가 삭제될 때에만 검사를 진행해주면 된다.
일단, 삭제된 노드의 색깔이 무엇인지 판단해보자.
2가지 경우로 나뉜다.
- 자식이 0개 또는 1개 있을 때 -> 원래 색
- 자식이 2개 있을 때 -> successor의 색
1번의 경우에는 원래 삭제하기 했던 노드 색깔 그대로 삭제된다.
하지만 2번의 경우에는 삭제되는 노드의 자리를 오른쪽 서브트리에서 가장 작은 값이 대체하게 되는데 이 대체하는 노드의 색깔이 삭제되는것이다.
간단하게 자리를 대체하는 노드가 자신의 색을 버리고 삭제된 노드의 색깔을 받기 때문이다.
그러면 이제 삭제된 색이 검은색이라 가정하고 #2, #4, #5를 위반했을 때 조정 방법을 알아보자.
삭제된 색이 검은색이라면 해당 노드를 대체하는 노드에 extra black을 부여한다. 검은색이 사라져서 문제가 된것이니 extra black을 부여해서 검은색을 다시 채워넣는다면 괜찮지 않을까하는 생각으로 시작된다.
그러면 이제 이 extra black을 어떻게 처리해줄지가 관건이다.
원래 삭제하려던 노드를 origin, 이 노드를 대체하는 노드를 target, target의 자리를 대체하는 노드를 sub_node라 하겠다.
origin의 자식이 0개 또는 1개라면 target = origin으로 같으며 sub_node는 target->left 또는 target->right가 될 것이다.
자식이 2개라면 target = successor가 되고, sub_node는 successor->right가 될 것이다. successor의 left는 존재할 수가 없다. 애초에 successor가 가장 왼쪽에 있는 노드이기 때문이다.
- RED + extra black -> red and black일 때
= BLACK으로 바꿔주면 끝.- BLACK + extra black -> doubly black일 때
= case.1, case.2, case.3, case.4로 나누어 해결방안을 따른다.
이제 각 case는 어떤 조건이며 어떻게 해결하는지 알아보자.
case. 4
형제가 black이고 형제의 red 자식이 뻗은 형태로 있을 때
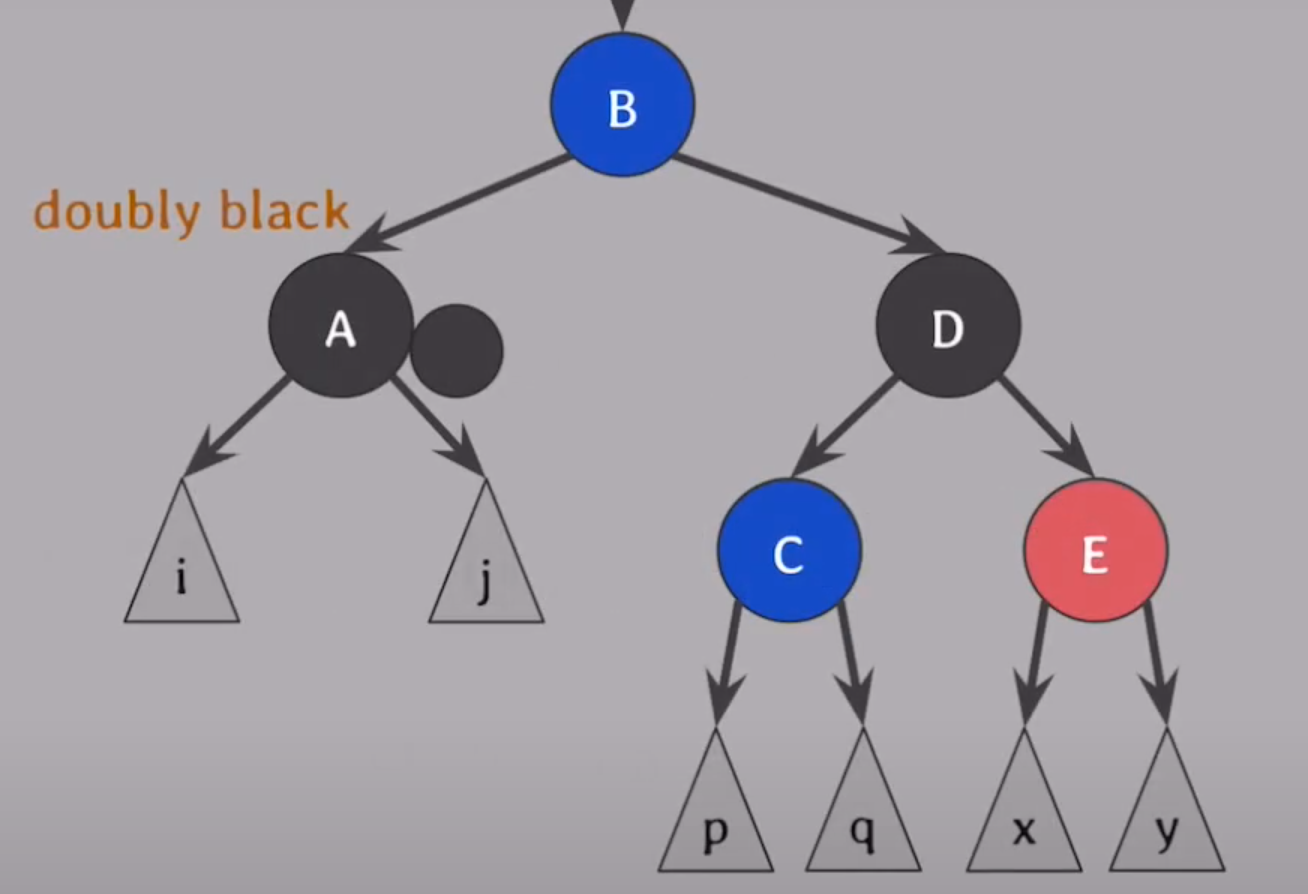
- 형제에 부모의 색을 준다.
- 부모와 형제의 red 자식의 색을 black으로 바꿔준다.
- 회전한다.
case. 3
형제가 black이고 형제의 red 자식이 꺾인 형태로 있을 때
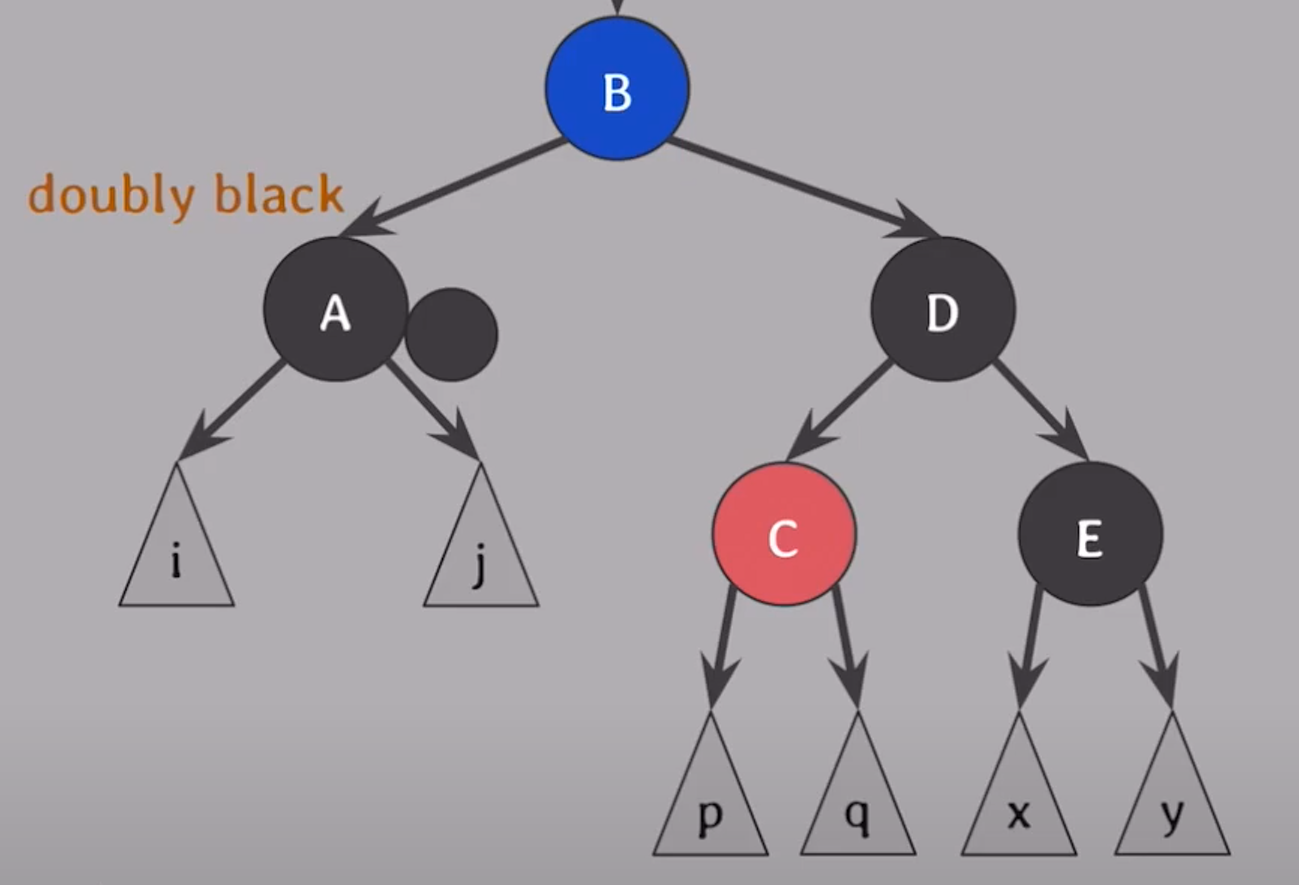
- 형제와 형제의 red 자식의 색을 바꾼다.
- 회전하여 case. 4의 형태로 만든다
- case. 4와 동일하게 해결한다.
case. 2
형제가 black이고 형제의 자식 모두 black일 때
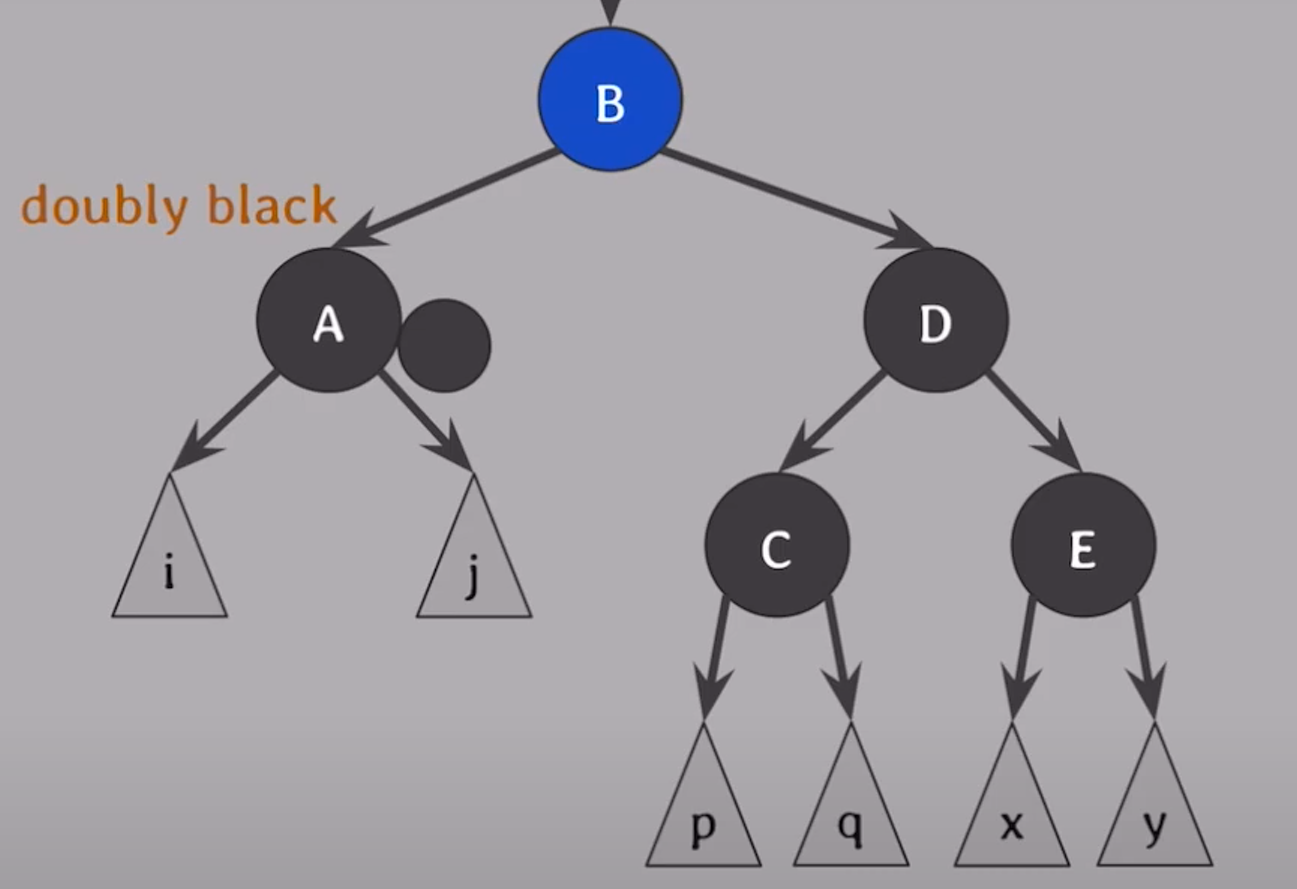
- 공통 속성인 extra black과 형제의 black을 부모에 전달한다. (형제는 red로 바뀜)
- 부모 + extra black을 재검사해준다.
case. 1
형제가 red일 때
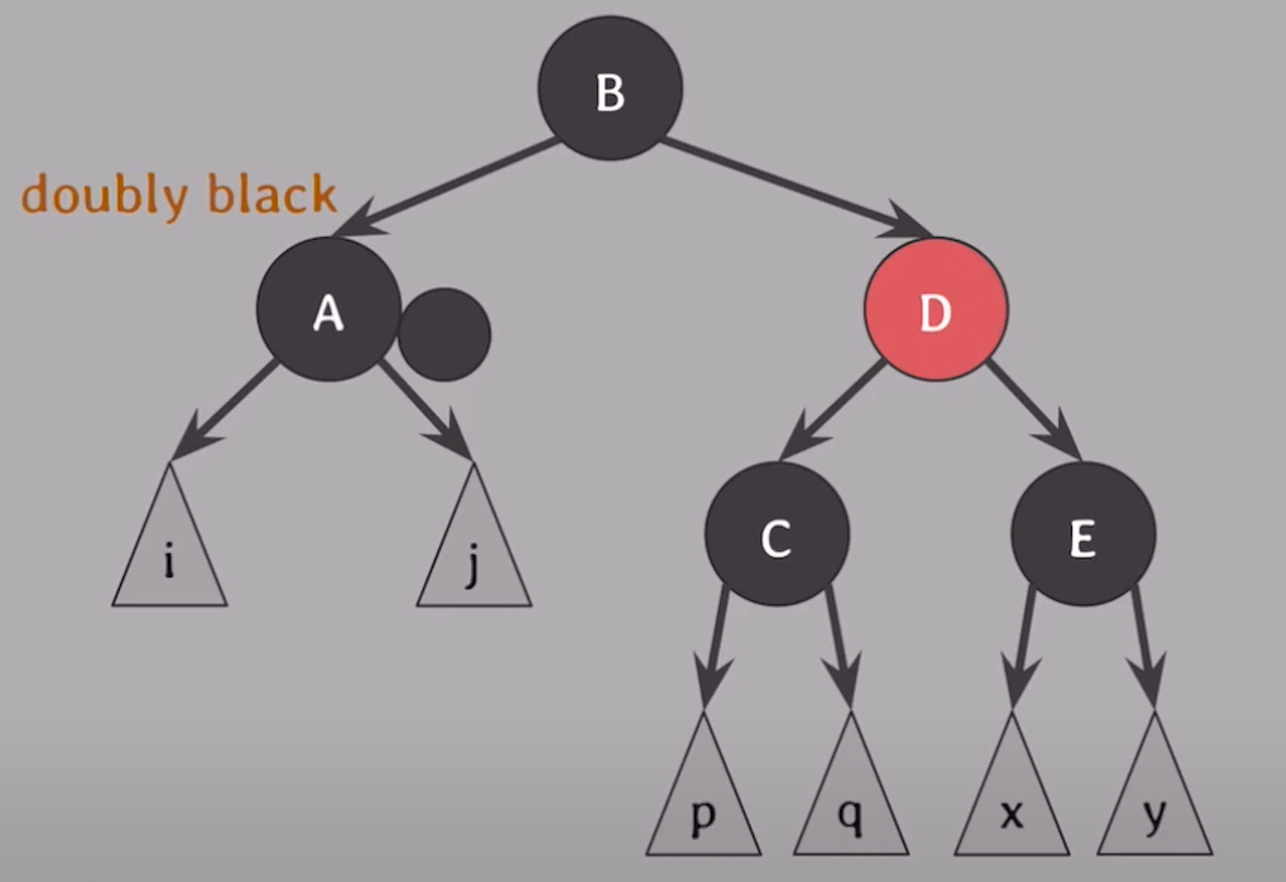
- 부모와 형제의 색을 바꾼다.
- 회전한다.
- case 2,3,4 해결방안을 따른다.
-> 회전하게 되면 해당 그림에서는 C가 A의 형제가 된다. 즉, A에게 검은색의 형제가 생긴다.
[삭제 예제 링크]
https://youtu.be/6drLl777k-E?t=1622
코드
void rbtree_transplant(rbtree *t, node_t *empty, node_t *replace) {
// empty 노드가 root였다면
// root는 replace가 된다
if (empty->parent == t->nil)
t->root = replace;
// empty의 부모가 replace를 자식으로 가르키게 한다
else if (empty == empty->parent->left)
empty->parent->left = replace;
else
empty->parent->right = replace;
// replace가 empty의 부모를 부모로 가르키게 한다
replace->parent = empty->parent;
}erase 함수를 소개하기전 먼저 알아야 할 함수이다.
empty 노드를 replace 노드가 대체한다. erase 함수를 작성하다 transplant 함수로 인해 헷갈렸는데 해당 함수의 기능은 정확히 아래와 같다.
empty를 가르키던 모든 연결을 끊고 empty의 부모와 replace를 연결해준다.
empty를 가르키던 연결이 끊긴거지 empty가 가르키던 것들은 살아있는 상태이다.
이제 erase 함수를 살펴보자.
int rbtree_erase(rbtree *t, node_t *origin) {
// 삭제할 노드
node_t *target = origin;
// 삭제될 색깔
color_t erased_color = target->color;
// target을 대체하는 노드
node_t *erased_sub_node = t->nil;
// 자식이 없을 때 or 1개만 있을 때
if (target->left == t->nil) {
erased_sub_node = target->right;
rbtree_transplant(t, target, erased_sub_node);
}
else if (target->right == t->nil) {
erased_sub_node = target->left;
rbtree_transplant(t, target, erased_sub_node);
}
// 자식이 2개일 때
else {
// 삭제 노드 갱신, 우측 서브트리 중 가장 작은 값
target = rbtree_successor(t, target->right);
erased_color = target->color;
// 우측 서브트리에서 left로만 빠졌기 때문에 오른쪽 자식만 존재
erased_sub_node = target->right;
// target과 child를 바꿔줌
// 자식이 0개 또는 1개일 때와 같으니 추가작업 필요 X
rbtree_transplant(t, target, erased_sub_node); /////////////////////////////
// 처음 삭제하려했던 p와 target을 바꿔줄거임
// p의 부모와 target은 transplant를 통해 연결될거임
// target의 자식을 갱신해주는 추가 작업 필요
rbtree_transplant(t, origin, target); //////////////////////////////////////
target->right = origin->right; /////////////////////////////////////////////
target->right->parent = target; ////////////////////////////////////////////
target->left = origin->left; ///////////////////////////////////////////////
target->left->parent = target; /////////////////////////////////////////////
target->color = origin->color; /////////////////////////////////////////////
}
if (erased_color == RBTREE_BLACK)
rbtree_erase_fixup(t, erased_sub_node);
free(origin);
return 0;
}본 글에서의 모든 코드는 교재의 pseudo code를 참고하였는데, 원래는 erase함수에 ///을 달아준 구역의 코드는 다음과 같았다.
if (target->parent == origin)
erased_sub_node->parent = target;
else {
rbtree_transplant(t, target, erased_sub_node);
target->right = origin->right;
target->right->parent = target;
}
rbtree_transplant(t, origin, target);
target->left = origin->left;
target->left->parent = target;
target->color = p->color;
아마 이런 경우를 따로 특정해준거 같다. 이 경우에 3노드의 오른쪽 erased_sub_node는 t->nil이고 extra black을 받게된다. erased_sub_node를 다른 가공없이 rbtree_erase_fixup(t, erased_sub_node)을 실행해주게 되면 extra black을 가진 노드의 parent를 검색하게 될때 바로 오류가 날것이다. 우리는 t->nil의 parent를 따로 설정해준적이 없기 때문이다.
origin의 successor가 origin의 자식이면 successor->right가 t->nil일 수도 있으니 successor->right->parent를 successor로 설정해줌으로써 rbtree_erase_fixup에서 오류를 막아준다고 생각한다. 이 작업을 진행해줄경우 else 구문의 몸체를 실행해줄 필요 없이 바로 아래 3줄만 실행하면 되는거 같다.
하지만 필자는 이러한 경우를 따로 나누어주는 것이 직관적으로 이해가 잘 되지 않아 if else를 빼버리고 else의 3줄을 항상 돌려주기로 했다.
erased_sub_node->parent = target;이 한줄로 특정 경우를 처리해 줄 수 있는 것을 필자는
rbtree_transplant(t, target, erased_sub_node);
target->right = origin->right;
target->right->parent = target;경우를 나눠주지 않고 이 3줄을 항상 돌려주기 때문에 조금 비효율적인 느낌이 있지만 이쪽이 이해가 더 잘가는것을 어쩌겠나....
RBTree 전체코드
// rbtree 생성
rbtree *new_rbtree(void) {
// rbtree를 위한 메모리 할당
// rbtree의 root와 nil 초기화
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
node_t *nil = (node_t *)calloc(1, sizeof(node_t));
nil->color = RBTREE_BLACK;
p->root = nil;
p->nil = nil;
return p;
}
// rbtree 해제
void delete_rbtree(rbtree *t) {
// root에서부터 삭제
node_t *now = t->root;
if (now != t->nil)
delete_node(t, now);
// root는 delete_node 호출 시 메모리 해제 됨
// rbtree의 nil은 따로 해제
free(t->nil);
free(t);
}
void delete_node(rbtree *t, node_t *node) {
if (node->left != t->nil)
delete_node(t, node->left);
if (node->right != t->nil)
delete_node(t, node->right);
// 전부 찾아서 메모리 해제
free(node);
}
// 노드 삽입
node_t *rbtree_insert(rbtree *t, const key_t key) {
// 현재 위치 노드 초기화
node_t *now = t->root;
// 현재노드의 부모노드로 사용할 변수 초기화
node_t *p = t->nil;
// 받은 키값을 가지는 노드 생성
node_t *node = (node_t *)calloc(1, sizeof(node_t));
node->key = key;
// 삽입될 적절한 위치 찾기
while (now != t->nil){
p = now;
if (node->key < now->key)
now = now->left;
else
now = now->right;
}
// node의 부모를 p로 설정
node->parent = p;
if (p == t->nil)
t->root = node;
// p의 자식을 node로 설정
else if (node->key < p->key)
p->left = node;
else
p->right = node;
node->left = t->nil;
node->right = t->nil;
node->color = RBTREE_RED;
// 룰 위반여부 검사
rbtree_insert_fixup(t, node);
return node;
}
void rbtree_insert_fixup(rbtree *t, node_t *node) {
// #4 위반 시 무한반복
while (node->parent->color == RBTREE_RED) {
// 할아버지 기준 좌측영역
if (node->parent == node->parent->parent->left) {
node_t *p_bro = node->parent->parent->right;
// case.1 부모의 형제가 RED일 때
if (p_bro->color == RBTREE_RED) {
// 할아버지 BLACK과 부모라인 RED 교환
node->parent->color = RBTREE_BLACK;
p_bro->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
// 할아버지 기준으로 #4 위반하는지 재검사
node = node->parent->parent;
}
// case.2, case.3 부모의 형제가 BLACK일 때
else {
// case.2 꺾인 형태일 때
if (node == node->parent->right) {
// 회전 후 case.3으로 만듦
node = node->parent;
rbtree_left_rotate(t, node);
}
// case.3 뻗은 형태일 때
// 할아버지 BLACK과 부모의 RED 교환 후 회전
node->parent->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
rbtree_right_rotate(t, node->parent->parent);
}
}
// 할아버지 기준 우측영역. 좌측영역의 대칭과 동일
else {
node_t *p_bro = node->parent->parent->left;
if (p_bro->color == RBTREE_RED) {
node->parent->color = RBTREE_BLACK;
p_bro->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
node = node->parent->parent;
}
else {
if (node == node->parent->left) {
node = node->parent;
rbtree_right_rotate(t, node);
}
node->parent->color = RBTREE_BLACK;
node->parent->parent->color = RBTREE_RED;
rbtree_left_rotate(t, node->parent->parent);
}
}
}
// #2를 위반 시 BLACK으로 바꿔주면 해결
t->root->color = RBTREE_BLACK;
}
void rbtree_left_rotate(rbtree *t, node_t *node) {
node_t *tmp = node->right;
// node와 tmp->left 상호연결
node->right = tmp->left;
if (tmp->left != t->nil)
tmp->left->parent = node;
// tmp와 node->parent 상호연결
tmp->parent = node->parent;
if (node->parent == t->nil)
t->root = tmp;
else if (node == node->parent->left)
node->parent->left = tmp;
else
node->parent->right = tmp;
// tmp와 node 상호연결
tmp->left = node;
node->parent = tmp;
}
void rbtree_right_rotate(rbtree *t, node_t *node) {
node_t *tmp = node->left;
// node와 tmp->right 상호연결
node->left = tmp->right;
if (tmp->right != t->nil)
tmp->right->parent = node;
// tmp와 node->parent 상호연결
tmp->parent = node->parent;
if (node->parent == t->nil)
t->root = tmp;
else if (node == node->parent->left)
node->parent->left = tmp;
else
node->parent->right = tmp;
// tmp와 node 상호연결
tmp->right = node;
node->parent = tmp;
}
// 노드 삭제
int rbtree_erase(rbtree *t, node_t *origin) {
// 현재 target은 원래 삭제하려던 노드 origin
node_t *target = origin;
// 실제 삭제될 색
color_t erased_color = target->color;
// 실제 삭제될 노드를 대체할 노드를 가르킬 변수
// 해당 노드에 extra black을 부여할거임
node_t *erased_sub_node = t->nil;
// 자식이 0개 or 1개
if (target->left == t->nil) {
erased_sub_node = target->right;
rbtree_transplant(t, target, erased_sub_node);
}
else if (target->right == t->nil) {
erased_sub_node = target->left;
rbtree_transplant(t, target, erased_sub_node);
}
// 자식이 2개
else {
// target이 successor로 바뀜
target = rbtree_successor(t, target->right);
erased_color = target->color;
erased_sub_node = target->right;
// origin, target, erased_sub_node 위치 변환
rbtree_transplant(t, target, erased_sub_node);
rbtree_transplant(t, origin, target);
target->right = origin->right;
target->right->parent = target;
target->left = origin->left;
target->left->parent = target;
target->color = origin->color;
}
// 삭제되는 색이 BLACK이라면 extra black을 처리해줄 추가작업
if (erased_color == RBTREE_BLACK)
rbtree_erase_fixup(t, erased_sub_node);
// 삭제되는거는 target의 색인거지 target 노드가 아님
// 삭제되는 노드는 origin임
free(origin);
return 0;
}
void rbtree_erase_fixup(rbtree *t, node_t *node) {
// doubly black이면 무한반복
// doubly black인데 root이면 탈출
while (node != t->root && node->color == RBTREE_BLACK) {
// 좌측영역
if (node == node->parent->left) {
node_t *bro = node->parent->right;
// case.1 형제가 RED일 때
if (bro->color == RBTREE_RED) {
// 부모 BLACK과 형제 RED 교환 후 회전
// case.2, case.3, case.4으로 변환
bro->color = RBTREE_BLACK;
node->parent->color = RBTREE_RED;
rbtree_left_rotate(t, node->parent);
bro = node->parent->right;
}
// case.2, case.3, case.4 형제가 BLACK일 때
// case.2 형제의 자식 모두 BLACK일 때
if (bro->left->color == RBTREE_BLACK && bro->right->color == RBTREE_BLACK) {
// 공통속성 나의 extra black과 형제의 BLACK을 부모에게 옮김
bro->color = RBTREE_RED;
// 부모가 extra black을 받았으니 재검사
node = node->parent;
}
else {
// case.3 형제의 왼쪽만 RED일 때
if (bro->left->color == RBTREE_RED) {
// 형제의 BLACK과 형제자식의 RED 교환 후 회전
//case.4로 변환
bro->left->color = RBTREE_BLACK;
bro->color = RBTREE_RED;
rbtree_right_rotate(t, bro);
bro = node->parent->right;
}
// case. 4
// 형제의 색을 부모의 색으로
// 부모와 형제의 RED자식을 BLACK으로
// 부모 기준 회전
bro->color = node->parent->color;
node->parent->color = RBTREE_BLACK;
bro->right->color = RBTREE_BLACK;
rbtree_left_rotate(t, node->parent);
// case.4를 해결 시 탈출을 위한 root로 초기화
node = t->root;
}
}
// 우측영역. 좌측영역의 대칭과 동일
else {
node_t *bro = node->parent->left;
if (bro->color == RBTREE_RED) {
bro->color = RBTREE_BLACK;
node->parent->color = RBTREE_RED;
rbtree_right_rotate(t, node->parent);
bro = node->parent->left;
}
if (bro->left->color == RBTREE_BLACK && bro->right->color == RBTREE_BLACK) {
bro->color = RBTREE_RED;
node = node->parent;
}
else {
if (bro->right->color == RBTREE_RED) {
bro->right->color = RBTREE_BLACK;
bro->color = RBTREE_RED;
rbtree_left_rotate(t, bro);
bro = node->parent->left;
}
bro->color = node->parent->color;
node->parent->color = RBTREE_BLACK;
bro->left->color = RBTREE_BLACK;
rbtree_right_rotate(t, node->parent);
node = t->root;
}
}
}
node->color = RBTREE_BLACK;
}
void rbtree_transplant(rbtree *t, node_t *empty, node_t *replace) {
// replace와 empty->parent를 상호연결하는 함수
if (empty->parent == t->nil)
t->root = replace;
else if (empty == empty->parent->left)
empty->parent->left = replace;
else
empty->parent->right = replace;
replace->parent = empty->parent;
}
node_t *rbtree_successor(const rbtree *t, node_t *pivot) {
while (pivot->left != t->nil)
pivot = pivot->left;
return pivot;
}
// 나머지 함수들
node_t *rbtree_find(const rbtree *t, const key_t key) {
node_t *now = t->root;
while (now != t->nil) {
if (key == now->key)
return now;
else if (key < now->key)
now = now->left;
else
now = now->right;
}
return NULL;
}
node_t *rbtree_min(const rbtree *t) {
node_t *now = t->root;
while (now->left != t->nil)
now = now->left;
return now;
}
node_t *rbtree_max(const rbtree *t) {
node_t *now = t->root;
while (now->right != t->nil)
now = now->right;
return now;
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
// 오름차순 출력 -> 중위순회 -> inorder
int idx = 0;
rbtree_in_order(t, t->root, arr, &idx);
return 0;
}
void rbtree_in_order(const rbtree *t, node_t *now, key_t *arr, int *idx) {
if (now->left != t->nil) {
rbtree_in_order(t, now->left, arr, idx);
}
arr[*idx] = now->key;
*idx += 1;
if (now->right != t->nil)
rbtree_in_order(t, now->right, arr, idx);
}최종본은 위에 올린 코드와 살짝 다를 수 있기에 깃허브 주소를 올려놓겠다.
carrotcookie github
한눈에 모든 case 보기
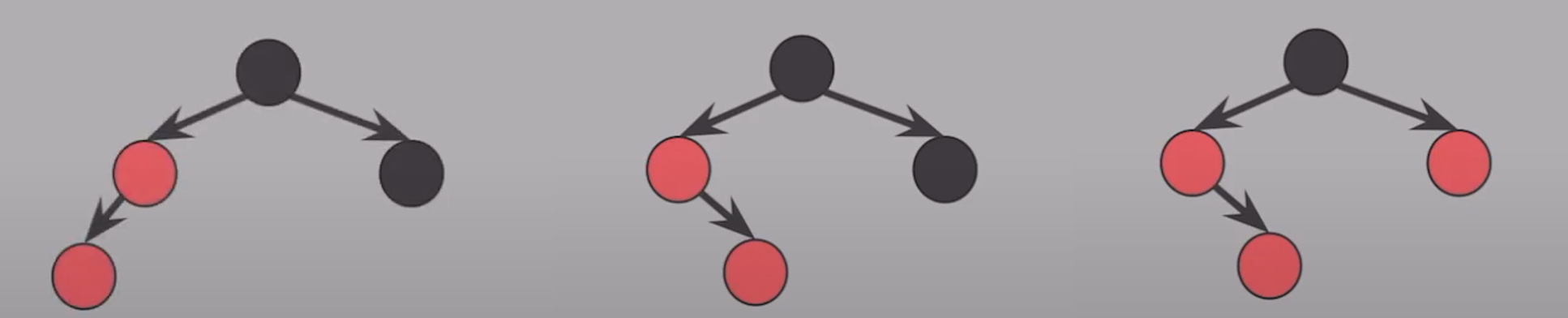
삽입 (case.3 -> case.2 -> case.1)
삭제 (case.4 -> case.3 -> case.2 -> case.1)

