Bubble Sort
버블 정렬이란 서로 인접한 두 원소의 크기를 비교 후, 조건에 따라 자리를 교환하는 정렬 알고리즘이다.
동작과정
코드 (bubble sort)
import sys
import random
input = sys.stdin.readline
def bubble_sort(a, n):
for i in range(n - 1):
for j in range(n - 1, i, -1):
if a[j] < a[j - 1]:
a[j], a[j - 1] = a[j - 1], a[j]
print(f'bubble_sort: {a}')
# 버블 정렬 개선
# 어느 패스에서 교환이 한번도 일어나지 않으면 종료
def bubble_sort_1(a, n):
for i in range(n - 1):
exchng = 0
for j in range(n - 1, i, -1):
if a[j] < a[j - 1]:
a[j], a[j - 1] = a[j - 1], a[j]
exchng += 1
if exchng == 0:
break
print(f'bubble_sort_1: {a}')
N = int(input())
arr = random.sample(range(1, N + 1), N)
print(f'정렬 전: {arr}')
bubble_sort(arr[:], N)
bubble_sort_1(arr[:], N)정렬 전: [10, 6, 8, 7, 3, 2, 9, 5, 1, 4]
bubble_sort: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
bubble_sort_1: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]과정을 살펴보면 다음과 같다.
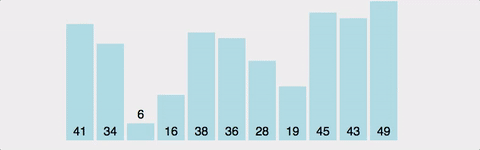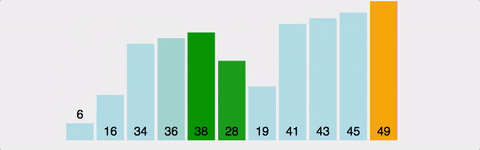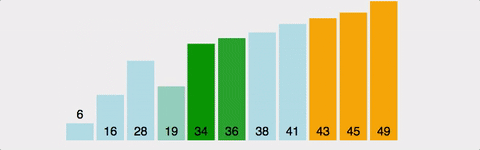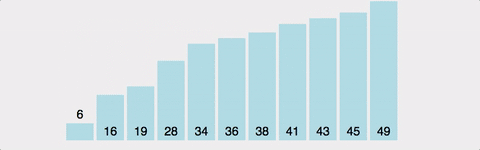
1 ~ 10까지의 숫자가 뒤죽박죽 섞여있다 가정하자.
- [9]값을 [0]까지 비교하면서 순서를 바꿔준다.
- [9]값을 [1]까지 비교하면서 순서를 바꿔준다.
.......- [9]값을 [8]까지 비교하면서 순서를 바꿔준다.
위의 과정을 총 n-1번 반복하게 된다.
bubble sort의 경우 시간 복잡도는 O(n^2)이다.
값이 같은 원소의 순서는 정렬한 후에도 같은 stable sort이다.
Selection Sort
가장 작은 원소부터 선택해 알맞은 위치로 옮기는 정렬 알고리즘이다.
동작과정

코드 (selection sort)
def selection_sort(a, n):
for i in range(n - 1):
# 가장 작은 원소의 인덱스
min = i
for j in range(i + 1, n):
if a[j] < a[min]:
min = j
a[i], a[min] = a[min], a[i]
print(f'정렬 후: {a}')
N = int(input())
arr = random.sample(range(1, N + 1), N)
print(f'정렬 전: {arr}')
selection_sort(arr[:], N)정렬 전: [2, 8, 7, 4, 9, 10, 5, 6, 1, 3]
정렬 후: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]과정은 다음과 같다.
- [0]값을 [9]까지 비교하면서 가장 작은 값을 가진 인덱스 캐싱 후 [0]값과 캐싱한값 교환
- [1]값을 [9]까지 비교하면서 가장 작은 값을 가진 인덱스 캐싱 후 [1]값과 캐싱한값 교환
.......- [8]값을 [9]까지 비교하면서 가장 작은 값을 가진 인덱스 캐싱 후 [1]값과 캐싱한값 교환
위의 과정을 총 n-1번 반복하게 된다.
selection sort의 경우 시간 복잡도는 O(n^2)이다.
서로 이웃하지 않는 떨어져 있는 원소를 교환하므로 unstable sort이다.
Insertion Sort
주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬하는 알고리즘이다.
동작과정

코드 (insertion sort)
import sys
import random
input = sys.stdin.readline
def insertion_sort(a, n):
for i in range(1, n):
j = i
tmp = a[i]
while j > 0 and a[j - 1] > tmp:
a[j] = a[j - 1]
j -= 1
a[j] = tmp
print(f'정렬 후: {a}')
N = int(input())
arr = random.sample(range(1, N + 1), N)
print(f'정렬 전: {arr}')
insertion_sort(arr[:], N)정렬 전: [3, 10, 7, 9, 2, 4, 8, 6, 5, 1]
정렬 후: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]과정은 다음과 같다.
- [1]값을 앞의 원소와 비교해서 작으면 계속 자리를 바꾸다 크거나 같은값을 만나면 멈추고 해당 자리에 삽입
- [2]값을 앞의 원소와 비교해서 작으면 계속 자리를 바꾸다 크거나 같은값을 만나면 멈추고 해당 자리에 삽입
.......- [9]값을 앞의 원소와 비교해서 작으면 계속 자리를 바꾸다 크거나 같은값을 만나면 멈추고 해당 자리에 삽입
위의 과정을 총 n-1번 반복하게 된다.
삽입 정렬의 경우 큰값을 만나게 되면 앞부분은 이미 정렬을 마쳤다는 보장이 있다.
거의 정렬이 완료된 배열을 대상으로는 속도가 굉장히 빠르다.
insertion sort의 경우 시간 복잡도는 O(n^2)이다.
서로 떨어져 있는 원소를 교환하지 않으므로 stable sort이다.
Quick Sort
투 포인터 분할 정렬 알고리즘이다. 중간 인덱스의 원소를 기준으로 정렬을 진행하다 포인터끼리 교차했을 때 두 그룹으로 나누어 각각 똑같은 과정을 진행해준다.
동작과정

코드 (quick sort)
import sys
import random
input = sys.stdin.readline
def quick_sort(a, left, right):
pl = left
pr = right
pivot_val = a[(left + right) // 2]
while pl <= pr:
while a[pl] < pivot_val: pl += 1
while a[pr] > pivot_val: pr -= 1
if pl <= pr:
a[pl], a[pr] = a[pr], a[pl]
pl += 1
pr -= 1
if left < pr: quick_sort(a, left, pr)
if pl < right: quick_sort(a, pl, right)
N = int(input())
arr = random.sample(range(1, N + 1), N)
sorted_arr = arr[:]
print(f'정렬 전: {arr}')
quick_sort(sorted_arr, 0, N - 1)
print(f'정렬 전: {sorted_arr}')정렬 전: [7, 3, 5, 6, 10, 1, 9, 8, 4, 2]
정렬 전: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]과정을 글로 설명하겠다.
좌측 포인터가 가르키는 값이 피벗값과 같거나 클때까지 옮긴다.
우측 포인터가 가르키는 값이 피벗값과 같거나 작을때까지 옮긴다.
그 때 좌측 포인터와 우측 포인터의 위치를 비교하고 값을 교환해주고 다시 옮겨준다.
위 과정을 두 포인터가 교차할 때까지 진행한다.
교차하고 나면 두 그룹으로 나누어 똑같이 진행해준다.
시간 복잡도는 O(nlogn)이다. 최악의 경우에는 O(n^2)이다.
unstable sort이다.
Merge Sort
배열을 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘이다.
동작과정

코드 (merge sort)
import sys
import random
input = sys.stdin.readline
def merge_sort(a, left, right):
def _merge_sort(a, left, mid, right):
i = left
j = mid + 1
k = left
while i <= mid and j <= right:
if a[i] < a[j]:
sorted[k] = a[i]
i += 1
else:
sorted[k] = a[j]
j += 1
k += 1
if i > mid:
for t in range(j, right + 1):
sorted[k] = a[t]
k += 1
else:
for t in range(i, mid + 1):
sorted[k] = a[t]
k += 1
for t in range(left, right + 1):
a[t] = sorted[t]
if left < right:
sorted = [0] * N
mid = (left + right) // 2
merge_sort(a, left, mid)
merge_sort(a, mid + 1, right)
_merge_sort(a, left, mid, right)
N = int(input())
arr = random.sample(range(1, N + 1), N)
sorted_arr = arr[:]
print(f'정렬 전: {arr}')
merge_sort(sorted_arr, 0, N - 1)
print(f'정렬 전: {sorted_arr}')정렬 전: [9, 4, 8, 7, 10, 6, 2, 5, 3, 1]
정렬 전: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]분할을 마치고 병합을 하는게 키포인트이다.
현재의 나는 이해한 상태나 혹시나 까먹었을 때를 대비해 코드를 참고했던 영상 링크를 걸겠다.
https://youtu.be/ctkuGoJPmAE?t=394
시간 복잡도는 O(nlogn)이고, stable sort이다.
Heap Sort
완전 이진 트리의 특성을 이용하여 정렬하는 알고리즘이다.
동작과정

코드 (heap sort)
import sys
import random
input = sys.stdin.readline
def heap_sort(a):
def down_heap(a, start, end):
temp = a[start]
parent = start
while parent < (end + 1) // 2:
cl = parent * 2 + 1
cr = cl + 1
child = cr if cr <= end and a[cr] > a[cl] else cl
if temp >= a[child]:
break
a[parent] = a[child]
parent = child
a[parent] = temp
n = len(a)
for i in range(n // 2, -1, -1):
down_heap(a, i, n - 1)
for i in range(n-1, 0, -1):
a[0], a[i] = a[i], a[0]
down_heap(a, 0, i - 1)
N = int(input())
arr = random.sample(range(1, N + 1), N)
sorted_arr = arr[:]
print(f'정렬 전: {arr}')
heap_sort(sorted_arr)
print(f'정렬 전: {sorted_arr}')정렬 전: [1, 3, 9, 8, 6, 7, 10, 4, 5, 2]
정렬 전: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]필자는 down_heap 방식으로 힙 상태를 만들어 주었다.
내가 이해한 방식대로 적어보겠다.
부모노드가 될 수 있는 노드 중 마지막 노드부터 자신의 값과 자식의 값을 비교하여 작다면 끌어내려서 적절한 자리를 찾아가도록 하는 방식이다.
모든 부모노드를 대상으로 1번씩 down_heap을 진행해주면 완전 이진 트리 상태가 된다. 이 상태가 되면 root노드의 값이 최대값이 된다. 그러면 첫번째 원소와 마지막 원소를 교환 해주고 다시 루트 노드를 대상으로 down_heap을 한번 진행해주면 된다.
즉, 값을 교환할 때마다 루트 노드를 대상으로 down_heap을 진행해주어야 한다.
up_heap도 구현할 줄 알아야한다. 아무것도 없는 상태에서 배열에 값을 추가하면서 힙을 만들기 위해서는 up_heap을 사용해야하기 때문이다.
시간 복잡도는 O(nlogn)이고, unstable sort이다.
참고 코드 (heapify)
def heapify_up():
n = len(a)
start = n - 1
child = start
tmp = a[start]
while child > 0:
parent = (child - 1) // 2
if a[parent] >= tmp:
break
a[child] = a[parent]
child = parent
a[child] = tmp
def heapify_down():
n = len(a)
if n == 0:
return
start = 0
parent = start
tmp = a[start]
while parent < n // 2:
cl = parent * 2 + 1
cr = cl + 1
if cr > n-1:
child = cl
else:
child = cr if a[cr] > a[cl] else cl
if a[child] <= tmp:
break
a[parent] = a[child]
parent = child
a[parent] = tmpCounting Sort
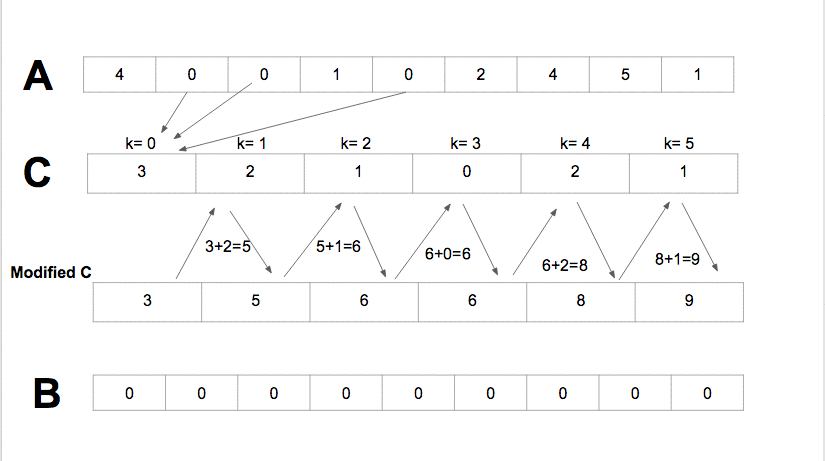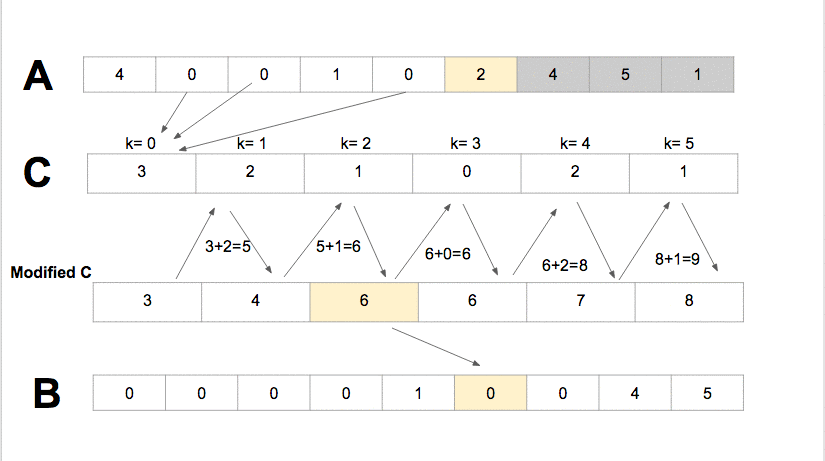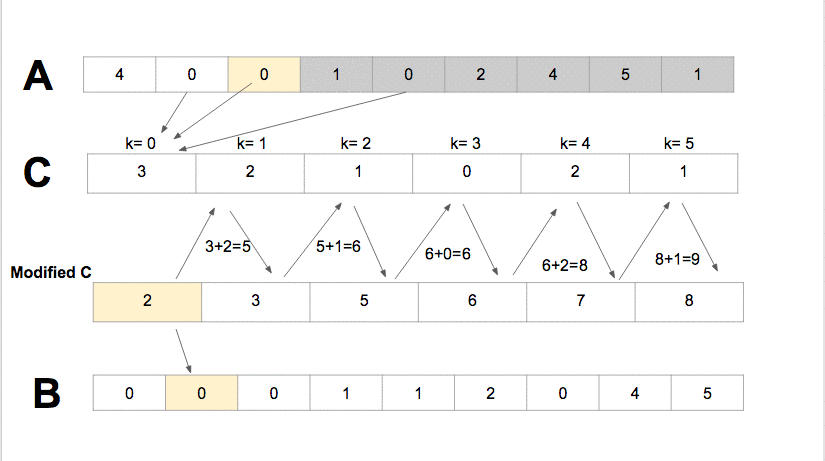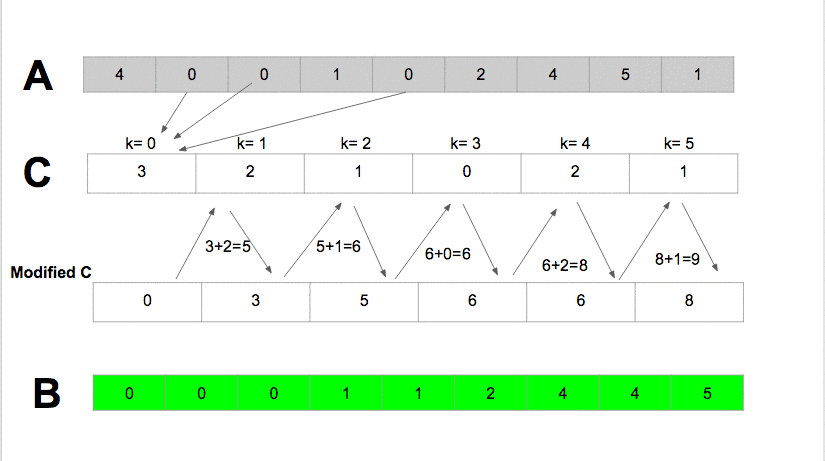
원소의 대소 관계를 판단하지 않고 빠르게 정렬하는 알고리즘이다.
동작과정
코드 (counting sort)
import sys
import random
input = sys.stdin.readline
def counting_sort(a):
def fsort(a, max):
n = len(a)
f = [0] * (max + 1)
b = [0] * n
for i in range(n): f[a[i]] += 1
for i in range(1, max + 1): f[i] += f[i-1]
for i in range(n-1, -1, -1): f[a[i]] -= 1; b[f[a[i]]] = a[i]
for i in range(n): a[i] = b[i]
fsort(a, max(a))
N = int(input())
arr = random.sample(range(1, N + 1), N)
sorted_arr = arr[:]
print(f'정렬 전: {arr}')
counting_sort(sorted_arr)
print(f'정렬 전: {sorted_arr}')정렬 전: [3, 8, 5, 9, 10, 7, 4, 2, 1, 6]
정렬 전: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 먼저 배열의 값중 가장 큰값의 길이만큼의 f배열을 0으로 초기화 하여 만들어준다.
- 배열의 앞에서 부터 값을 읽어나가면서 값을 인덱스로 가지는 f의 값을 1씩 증가시켜준다.
- 누적 도수 분포표를 만든다. 결과를 저장할 배열 b를 만든다.
- 원래 배열의 뒤에서부터 값을 인덱스로 가지는 f, 그 f의 값-1을 인덱스로 가지는 b의 값을 원래 배열의 값으로 한다.
시간 복잡도는 O(n)이다.
3번째 for문에서 스캔을 뒤부터 해주고 있는데 이 때만 stable sort이고, 앞에서부터 스캔하는 방식으로 구현한다면 unstable sort이다.
정렬 알고리즘 속도 비교

