[학습] AVL-Tree, B-Tree

AVL Tree

AVL 트리의 특징은 다음과 같다.

1. 이진 탐색 트리의 한 종류이다.
2. 스스로 균형을 잡는 트리이다.
3. balance factor를 통해 균형 유지한다.

임의의 노드 x가 있을 때 x노드의 balance factor는 (왼쪽 서브트리의 높이 - 오른쪽 서브트리의 높이)가 된다. 앞으로 노드 x의 balance factor는 BF(x)라 표현하겠다.

BF(x)가 -1, 0, 1의 값만 가질 수 있도록 어느 한쪽으로 기울지 않게 균형을 잡는것이다.

예를 들어보자.

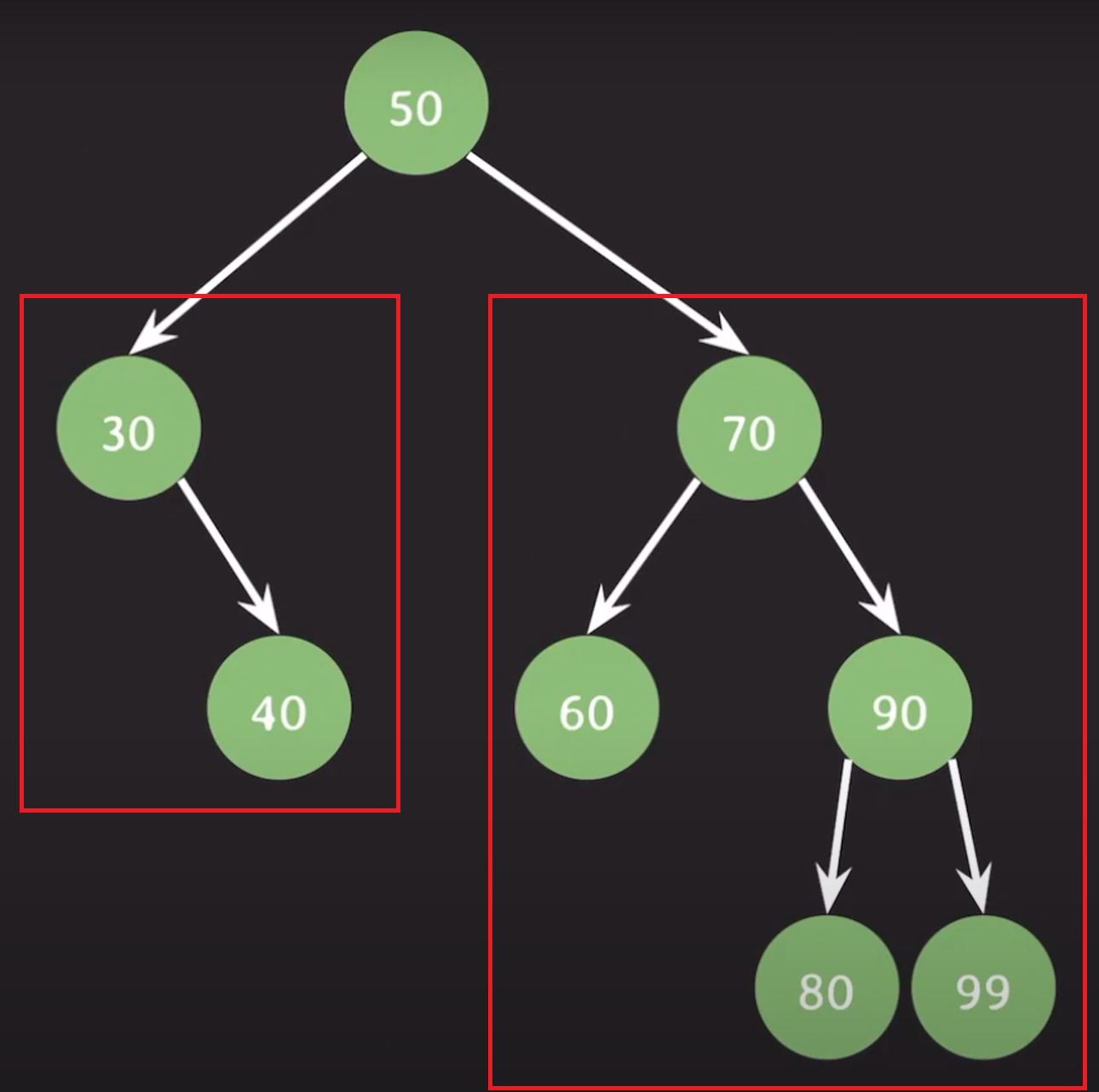
BF(50)은 왼쪽 서브트리의 높이 1, 오른쪽 서브트리의 높이 2
BF(50) = 1 - 2 = -1이 된다.
만약 서브트리가 없다면 서브트리의 높이는 -1이다.

RB Tree를 이해한 상태라면 AVL Tree의 이해는 원활할거라 생각한다.

노드의 삽입과 삭제과정은 이진트리와 같다.
삽입의 경우 해당 key값의 노드가 들어갈 적절한 위치를 찾아서 넣어주고 균형이 맞는지 확인하는 작업을 거친다.
삭제의 경우 해당 key값을 갖는 노드를 찾아 삭제 후 균형이 맞는지 확인한다.

균형을 맞추는 작업은 RB Tree에서 사용했던 rotate함수를 사용하면 된다.
새 노드 new_node를 삽입했다 가정하자. new_node의 parent부터 root 노드까지 거슬러 올라가면서 balance factor를 확인하고 -1, 0, 1 이외의 값을 갖는다면 rotate함수를 호출해 균형을 맞추는 작업이 이뤄진다.

new_node의 level을 5라 하고, root node의 level을 0이라 했을 때 BF(new_node->parent) != {-1, 0, 1} 이라면 rotate가 발생하고 이후의 부모노드부터 root까지 다시 검사를 해주면 된다. 이 경우 rotate를 마치고 BF(new_node->parent->parent)를 검사해주면 된다.

균형을 맞추기 위한 조정이 일어날 때 총 4가지의 형태가 있다. 각각의 형태에 따라 균형을 어떻게 맞추는지 살펴보겠다.

1. 오른쪽 오른쪽 편향

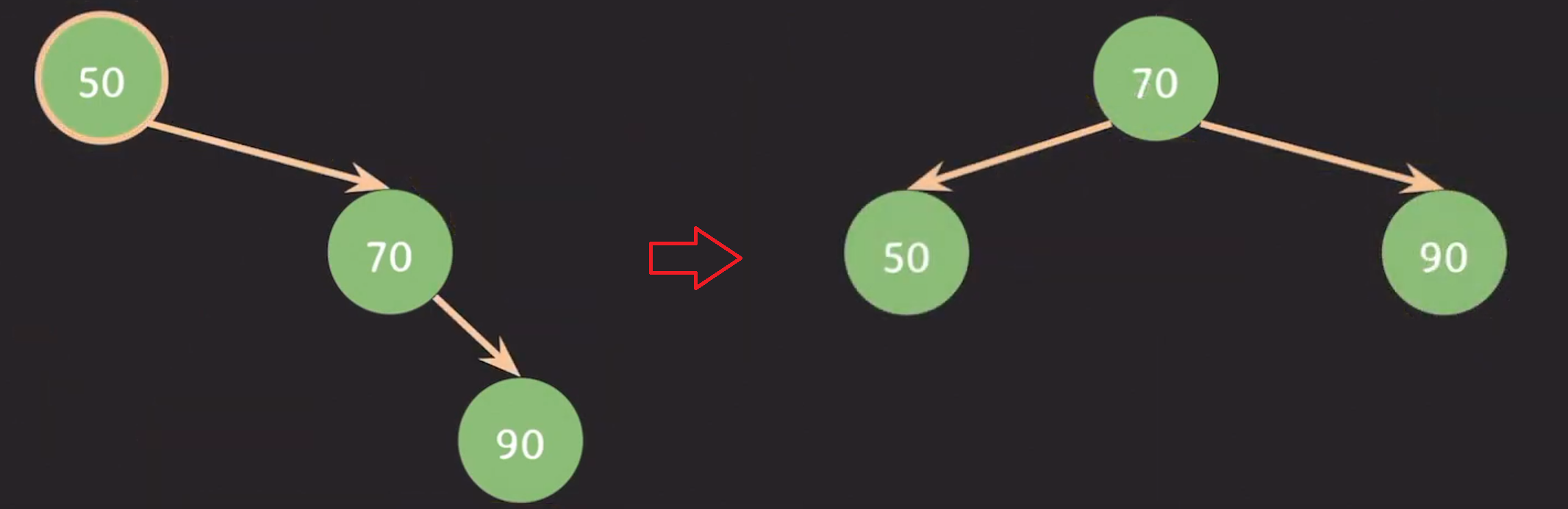
과정

1. 90을 삽입한다.
2. BF(70) = -1 - 0 = -1
3. BF(50) = -1 - 1 = -2 -> 조정필요

해결

1. 50을 기준으로 왼쪽 회전한다.
2. root 노드까지 balance factor 검사가 종료되었다.

2. 왼쪽 왼쪽 편향

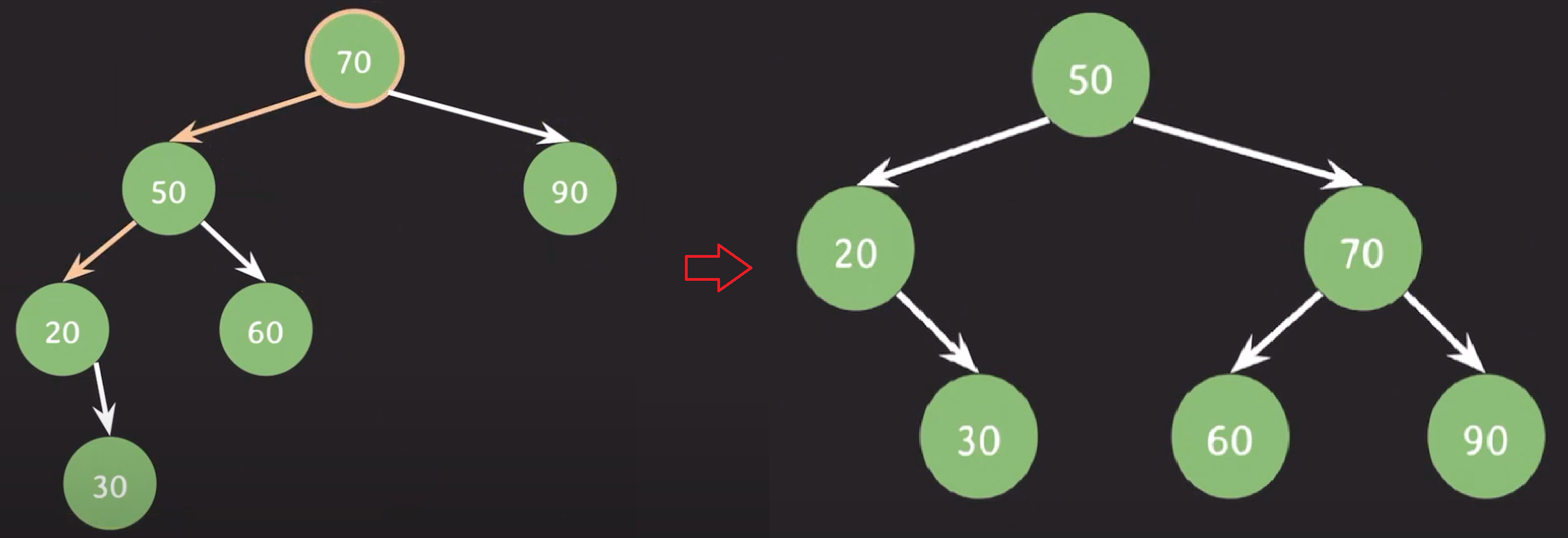
과정

1. 30을 삽입한다.
2. BF(20) = -1 - 0 = -1
3. BF(50) = 1 - 0 = 1
4. BF(70) = 2 - 0 = 2 -> 조정필요

해결

1. 70을 기준으로 오른쪽 회전한다.
2. root 노드까지 balance factor 검사가 종료되었다.

3. 오른쪽 왼쪽 편향

![]()

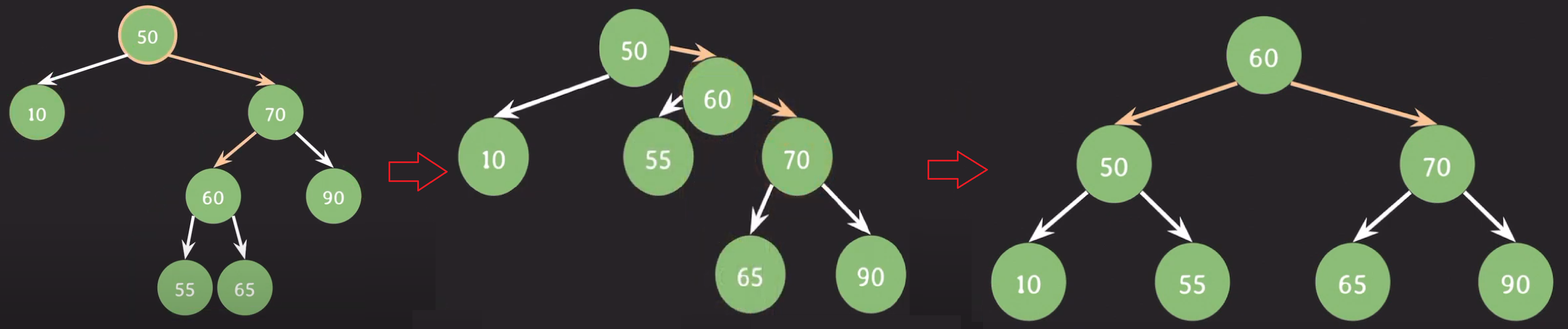
과정

1. 55를 삽입한다.
2. BF(60) = 0 - (-1) = 1
3. BF(70) = 1 - 0 = 1
4. BF(50) = 0 - 2 = -2 -> 조정필요

해결

1. 70을 기준으로 오른쪽 회전한다.
2. 60을 기준으로 왼쪽 회전한다.
3. root 노드까지 balance factor 검사가 종료되었다.

4. 왼쪽 오른쪽 편향

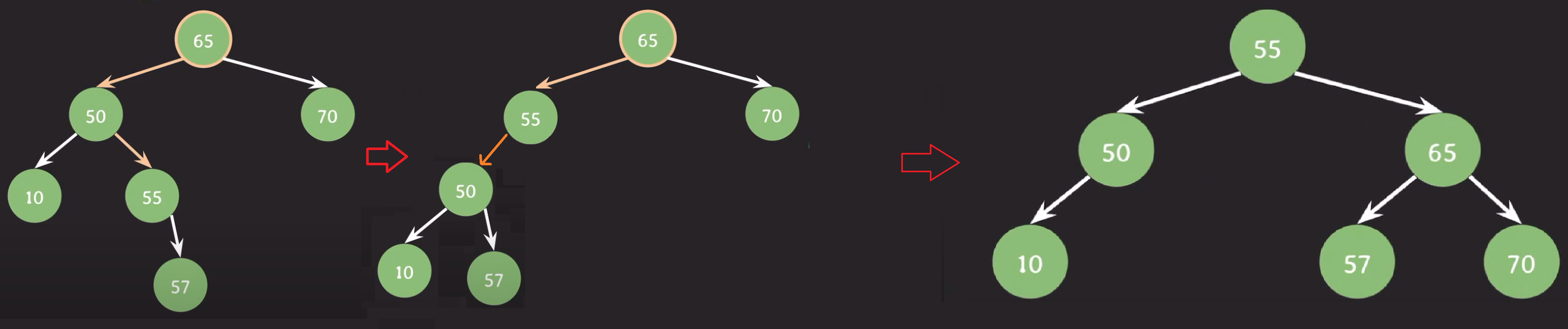
과정

1. 57을 삽입한다.
2. BF(55) = -1 - 0 = -1
3. BF(50) = 0 - 1 = -1
4. BF(65) = 2 - 0 = 2 -> 조정필요

해결

1. 50을 기준으로 왼쪽 회전한다.
2. 55를 기준으로 오른쪽 회전한다.
3. root 노드까지 balance factor 검사가 종료되었다.

예제 참고
https://youtu.be/syGPNOhsnI4?t=212

참고

유튜브 쉬운코드 - AVL 트리