[학습] 다익스트라, 플로이드 워셜

다익스트라

특정한 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산하는 알고리즘이다.
음의 간선이 없을 때 정상적으로 동작한다.

노드 개수 v, 간선 정보 e라 하였을 때 시간 복잡도는 O(elogv)이다.

1. 출발 노드를 설정한다.
2. 최단 거리 테이블을 초기화한다.
3. 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택한다.
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
5. 3번과 4번 과정을 반복한다.

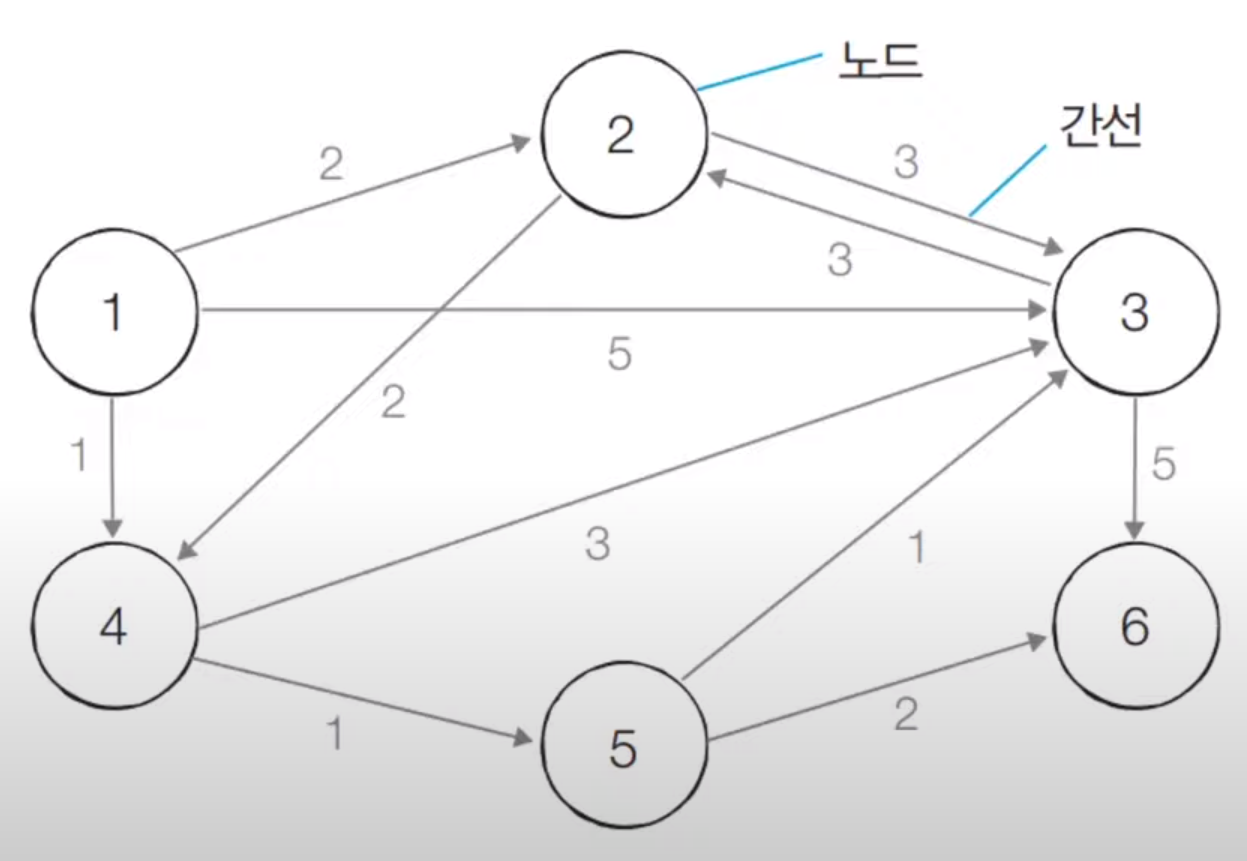
코드

def dijkstar(start):
    q = []
    heapq.heappush(q, (0, start))
    distance[start] = 0

    while q:
    	# 최단 거리가 가장 짧은 노드 선택
        dist, now = heapq.heappop(q)
		
        # 방문한 노드면 continue
        if distance[now] < dist: continue

        for i in graph[now]:
            cost = dist + i[1]
			
            # 최단 거리 테이블 갱신
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))

v = 6
edge = [(1, 2, 2), (1, 4, 1), (2, 3, 3), (2, 4, 2), (3, 2, 3), (3, 6, 5), (4, 3, 3), (4, 5, 1), (5, 3, 1), (5, 6, 2)]
graph = [[] for _ in range(v + 1)]
distance = [sys.maxsize] * (v + 1)

for start, end, cost in edge:
    graph[start].append((end, cost))

# 1번 노드를 시작지점으로 설정
dijkstar(1)

for i in range(1, v + 1):
    if distance[i] == sys.maxsize: continue
    print(distance[i], end = ' ')

-결과-
1번 -> 1번 최단거리: 0
1번 -> 2번 최단거리: 2
1번 -> 3번 최단거리: 3
1번 -> 4번 최단거리: 1
1번 -> 5번 최단거리: 2
1번 -> 6번 최단거리: 4

플로이드 워셜

모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다.
다이나믹 프로그래밍으로 분류된다.

점화식은 다음과 같다.

$DP_{ab} = min(DP_{ab}, DP_{ak} + DP_{kb})$

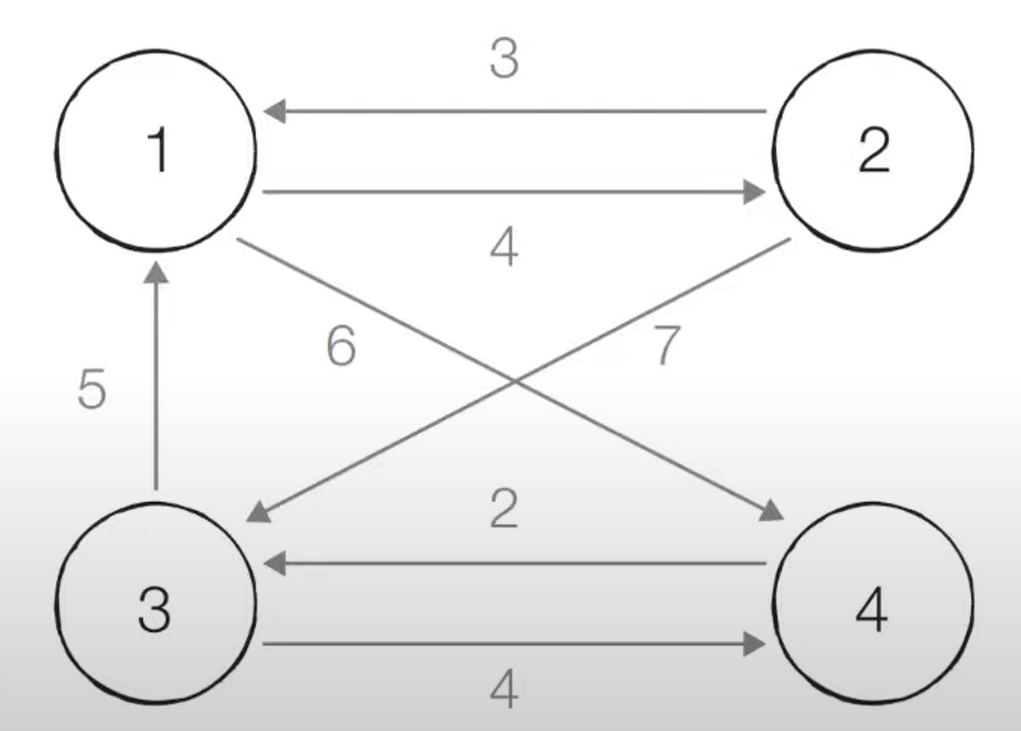
2차원 배열을 통해 위의 점화식을 나타내줄거다.
DP[i][j]는 i노드에서 j노드까지의 최단거리를 의미한다.

즉, 점화식은 i에서 j로 가는경로를 계산할 때 k를 거쳐서 가는게 더 빠르다면 갱신을 해주는거다.

코드

v = 4
edge = [(1, 2, 4), (1, 4, 6), (2, 1, 3), (2, 3, 7), (3, 1, 5), (3, 4, 4), (4, 3, 2)]
graph = [[sys.maxsize] * (v + 1) for _ in range(v + 1)]

for i in range(1, v + 1):
    for j in range(1, v + 1):
        if i == j: graph[i][j] = 0

for start, end, cost in edge:
    graph[start][end] = cost

for k in range(1, v + 1):
    for i in range(1, v + 1):
        for j in range(1, v + 1):
            graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])

for row in graph[1:]:
    print(*(row[1:]))

-결과-
0 4 8 6
3 0 7 9
5 9 0 4
7 11 2 0

시간 복잡도는 O($n^3$)이다