[기초수학] Chapter01. 기초수학(약수, 소수, 소인수분해, 최대공약수, 최소공배수, 수열)

황성미·2023년 7월 16일

기초수학 제로베이스 제로베이스데이터스쿨 제로베이스스쿨 파이썬 파이썬기초

제로베이스 데이터스쿨

목록 보기

9/58

✍🏻 16일 공부 이야기.

약수와 소수

약수 : 어떤 수를 나누어 떨어지게 하는 수

inputNumber = int(input("0보다 큰 정수 입력 : "))

for number in range(1, (inputNumber + 1)):
  if inputNumber % number == 0:
    print(f'{inputNumber}의 약수 : {number}')

💻출력
0보다 큰 정수 입력 : 15
15의 약수 : 1
15의 약수 : 3
15의 약수 : 5
15의 약수 : 15

소수 : 1과 자신만을 약수로 가지는 수(단, 1은 제외)
예제. 2부터 입력한 숫자까지의 소수를 찾는 방법

inputNumber = int(input("0보다 큰 정수 입력 : "))

#2부터 입력한 숫자까지의 소수를 찾는 방법
for number in range(2, (inputNumber + 1)):
  prime = True

  #소수 판별법
  for n in range(2, number):
    if number % n == 0:
      prime = False
      break

  if prime == True:
    print(f'{number} : 소수 !!')
  else:
    print(f'{number} : 합성수 !!') #소수가 아닌 수를 합성수라 부름

💻출력
0보다 큰 정수 입력 : 10
2 : 소수 !!
3 : 소수 !!
4 : 합성수 !!
5 : 소수 !!
6 : 합성수 !!
7 : 소수 !!
8 : 합성수 !!
9 : 합성수 !!
10 : 합성수 !!

소인수분해

소인수 : 약수 중에서 소수인 숫자
20의 약수(1,2,4,5,10,20) 중 소수는 2,5 이므로 2,5가 20의 소인수.
소인수분해 : 1보다 큰 정수를 소인수의 곱으로 나타낸 것
20 = 2 2 5

inputNumber = int(input("1보다 큰 정수 입력 : "))

n = 2
while n <= inputNumber: #2부터 입력한 숫자 중 소인수를 찾는 과정
  #소인수이면
  if inputNumber % n == 0:
    print(f'소인수 : {n}')
    inputNumber /= n #해당 숫자로 나눈후, 다시 또 소인수를 찾고
  #소인수가 아니면
  else:
    n += 1 #1씩 숫자를 증가시키며 다른 소인수를 찾음

💻출력
1보다 큰 정수 입력 : 12
소인수 : 2
소인수 : 2
소인수 : 3

공약수와 최대공약수

공약수 : 두 개 이상의 수에서 공통된 약수
최대공약수 : 공약수 중 가장 큰 수

💡 공약수를 구하고자 하는 두 수의 소인수분해를 해두면,
좀 더 빨리 공약수와 최대공약수를 찾을 수 있다!

num1 = int(input('1보다 큰 정수 입력 : '))
num2 = int(input('1보다 큰 정수 입력 : '))
maxNum = 0

for i in range(1, (num1 + 1)): #1부터 num1 중 공약수 찾기
  #1부터 num1까지든, 1부터 num2까지 찾든 상관없음!
  if num1 % i == 0 and num2 % i == 0: #공약수이면
    print(f'공약수 : {i}')
    maxNum = i #최대공약수를 그 수로 업데이트해줌
print(f"최대공약수 : {maxNum}")

💻출력
1보다 큰 정수 입력 : 36
1보다 큰 정수 입력 : 12
공약수 : 1
공약수 : 2
공약수 : 3
공약수 : 4
공약수 : 6
공약수 : 12
최대공약수 : 12

💡 유클리드 호제법을 이용한 최대공약수 구하기
x, y의 최대공약수는 y, (x%y)의 최대공약수와 같다.

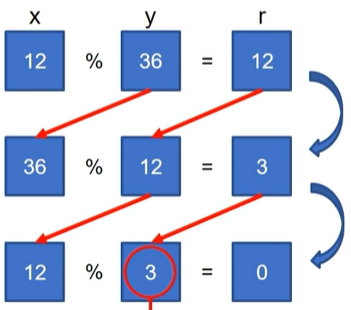
나머지(y)가 0일 때까지 나눗셈

num1 = int(input('1보다 큰 정수 입력 : '))
num2 = int(input('1보다 큰 정수 입력 : '))

x = num1; y = num2

while y > 0 : #최대공약수 구하기
  x2 = y #새롭게 x자리에 들어갈 변수
  y = x % y #나눗셈을 한 값은 새롭게 y 자리에 들어감
  x = x2 #x자리에 x2를 받음.
print(f'{num1}, {num2}의 최대공약수 : {x}')

for n in range(1, (x + 1)): #1부터 최대공약수까지 중에서
  if x % n == 0: #0으로 나누어 떨어지는 것은
    print(f'{num1}, {num2}의 공약수 : {n}') #둘의 공약수임을 뜻함

💻 출력
1보다 큰 정수 입력 : 12
1보다 큰 정수 입력 : 36
12, 36의 최대공약수 : 12
12, 36의 공약수 : 1
12, 36의 공약수 : 2
12, 36의 공약수 : 3
12, 36의 공약수 : 4
12, 36의 공약수 : 6
12, 36의 공약수 : 12

공배수와 최소공배수

공배수 : 두 개 이상의 수에서 공통된 배수
최소공배수 : 공배수 중 가장 작은 수

💡 소인수분해를 이용하여 구하는 방법

num1 = int(input('1보다 큰 정수 입력 : '))
num2 = int(input('1보다 큰 정수 입력 : '))
maxNum = 0

for i in range(1, (num1 + 1)): #1부터 num1 중 공약수 찾기
  if num1 % i == 0 and num2 % i == 0: 
    maxNum = i 
print(f"최대공약수 : {maxNum}")

#최소공배수는 (num1 * num2) // 최대공약수 로 구할 수 있음
minNum = (num1 * num2) // maxNum
print(f"최소공배수 : {minNum}")

💻 출력
1보다 큰 정수 입력 : 10
1보다 큰 정수 입력 : 12
최대공약수 : 2
최소공배수 : 60

수열

수열 : 규칙성을 가지고 나열되어있는 수들
등차 수열 : 연속된 두 항의 차이가 일정한 수열(an = a1 + (n-1) * d)
등차 중항 : 연속된 세 항에서 가운데 항
등차 수열의 합 Sn = n * (a1 + an) / 2

inputa1 = int(input('a1 입력 : '))
inputD = int(input('공차 입력 : '))
inputN = int(input("n 입력 : "))

an = 0
n = 1
while n <= inputN:
  if n == 1:
    an = inputa1
    print(f'{n}번째 항의 값 : {an}')
    n += 1
    continue
  an += inputD
  print(f'{n}번째 항의 값 : {an}')
  n += 1
print(f'{inputN}번째 항의 값 : {an}')