🚀 들어가기

이제 자료구조 마지막입니다. 저에게 힙이란 자료구조는 다소 낯선 존재입니다. 기말시험 범위가 아니었거나 마지막이라고 대충 공부해서 잊혀졌겠죠...

지난 자료구조 포스팅(트리)을 준비하면서 트리의 개념 및 동작을 열심히 익혔습니다. 이를 기반으로 힙에 대해 간략하면서 핵심을 살려 정리해보겠습니다!

✨ 힙

💡 개념

힙(Heap)은 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리입니다. 완전 이진 트리는 노드를 삽입 할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리입니다.

힙은 최대값을 구하기 위한 최대 힙 구조와 최소값을 구하기 위한 최소 힙 구조로 분류할 수 있습니다. 힙을 사용하면 최대값 또는 최소값을 빠르게 찾을 수 있습니다.

힙은 두 가지 조건을 가지고 있습니다.

1. 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다.(작거나 같다.)
2. 완전 이진 트리 형태를 갖는다.

지금까지 힙에 대한 설명을 보면서 지난 트리 자료구조에서 자세하게 알아본 이진 탐색 트리와 유사하다고 생각할 수 있습니다. 힙과 이진 탐색 트리는 둘 다 이진 트리라는 공통점이 있습니다.

하지만 차이점이 꽤 있는데요, 먼저 힙에는 이진 탐색 트리와 같은 조건이 없습니다. 이진 탐색 트리는 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건이 있지만 힙에는 적용되지 않습니다. 또 힙의 루트 노드는 해당 구조에서 가장 큰 값 또는 가장 작은 값을 갖고 있습니다.

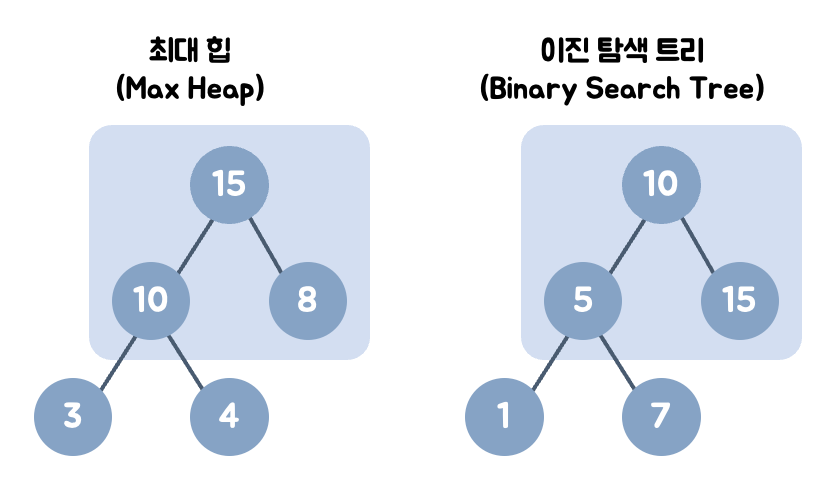
출처: https://velog.io/@gnwjd309/data-structure-heap

📗 설명

⏺️ 힙

이제 그림으로 힙에 대해 설명해보겠습니다. 최대 힙을 예시로 하겠습니다.

힙은 이진 탐색 트리와 같이 노드로 구성됩니다.

최대 힙은 노드의 값이 가장 큰 노드가 루트 노드의 위치에 있습니다.

⏺️ 힙의 동작

다음은 힙의 동작에 대해 알아보겠습니다. 먼저 힙의 삽입 입니다.

힙의 삽입

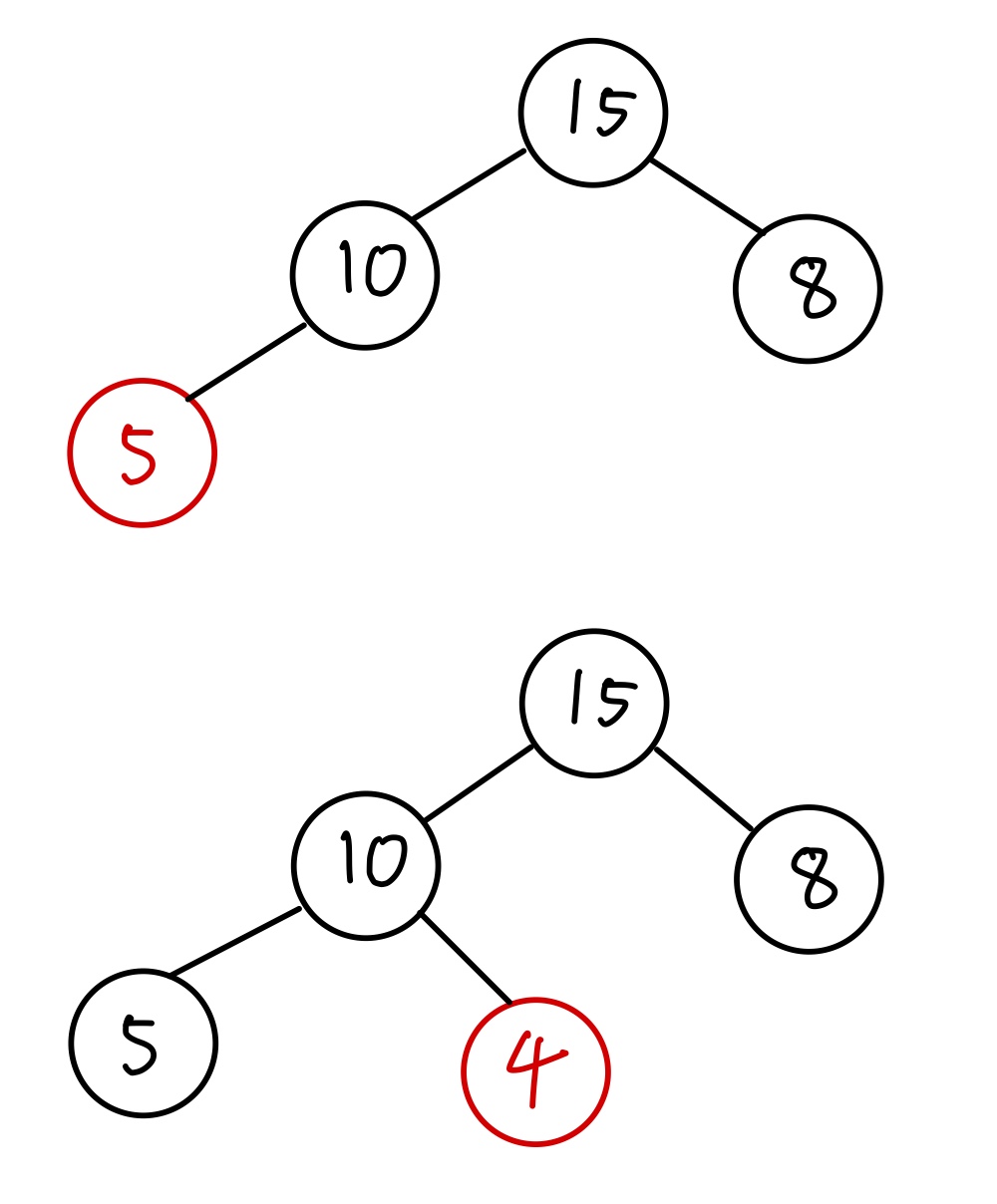
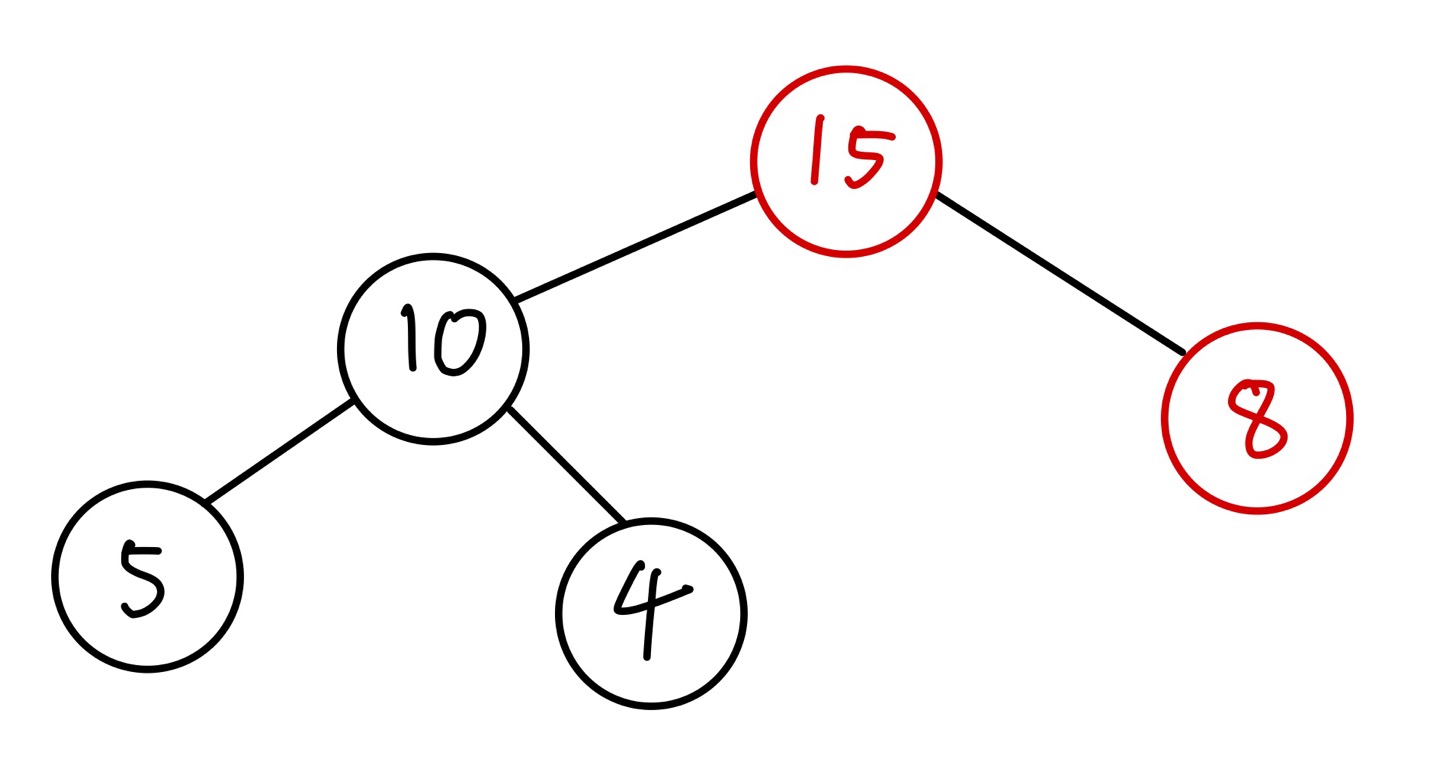
힙은 완전 이진 트리이므로 새로운 노드는 왼쪽 가장 하단에 위치됩니다. 15, 10, 8, 5, 4 순으로 삽입된다고 가정해보겠습니다.

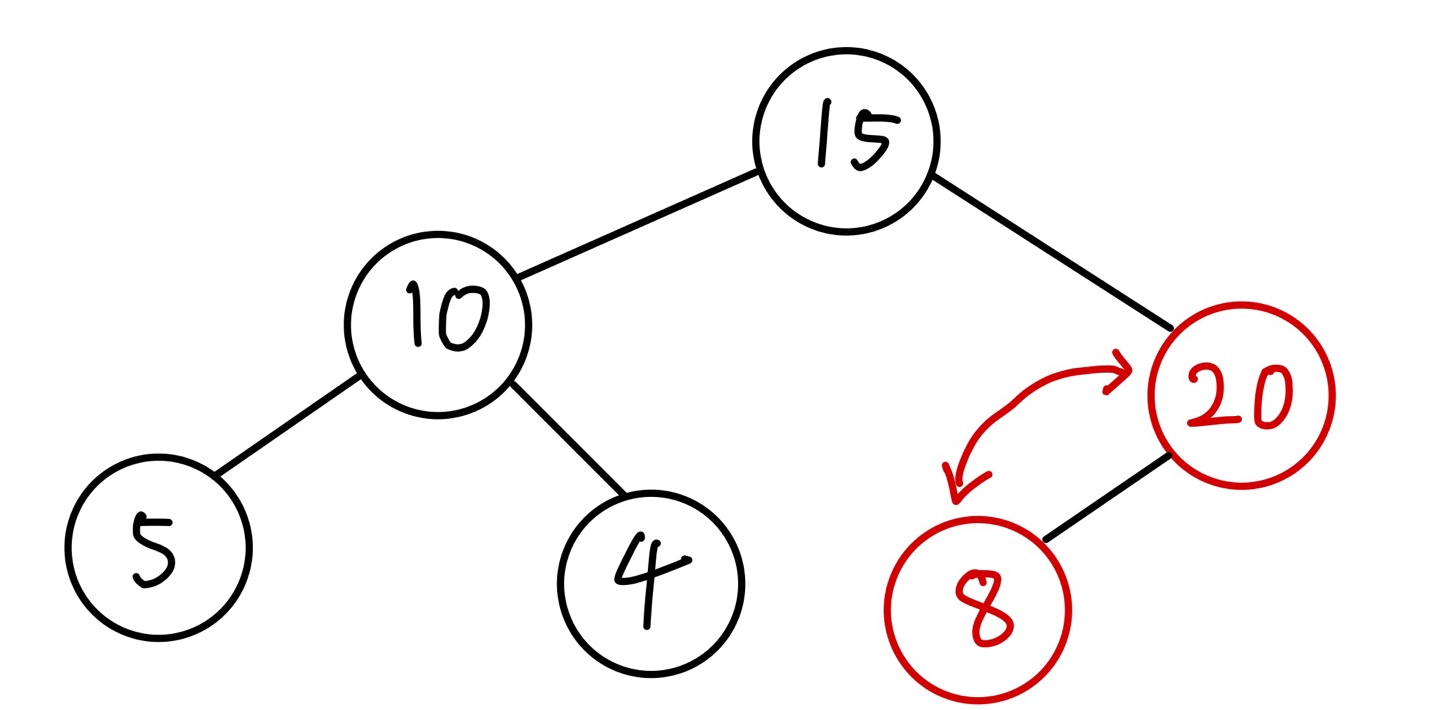
만약 새로운 노드가 루트 노드, 즉 현재 가장 큰 값을 갖고 있는 노드의 값보다 큰 값을 갖고 있다면 추가 동작이 필요합니다. 현재 최대 힙에서 가장 큰 값은 15입니다. 새로운 노드의 값이 20이라고 가정해보겠습니다.

먼저 일반적인 삽입 동작과 같이 왼쪽 가장 하단에 새로운 노드를 위치 시킵니다.

그 후 새로운 노드의 값이 부모 노드의 값보다 크다면 두 노드의 위치를 바꿉니다. 이 동작은 새로운 노드의 값이 부모 노드의 값보다 작거나 같을 때까지 반복합니다.

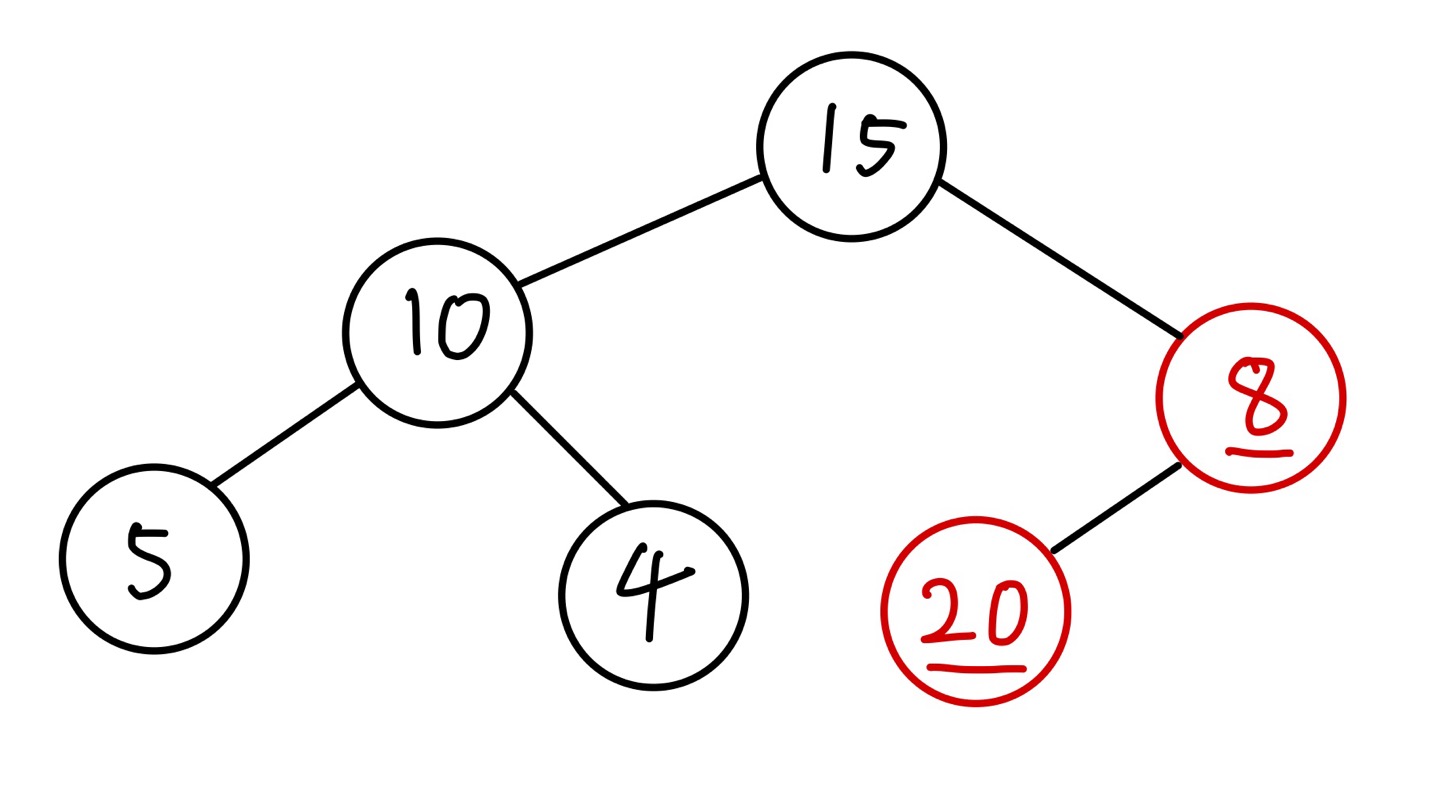
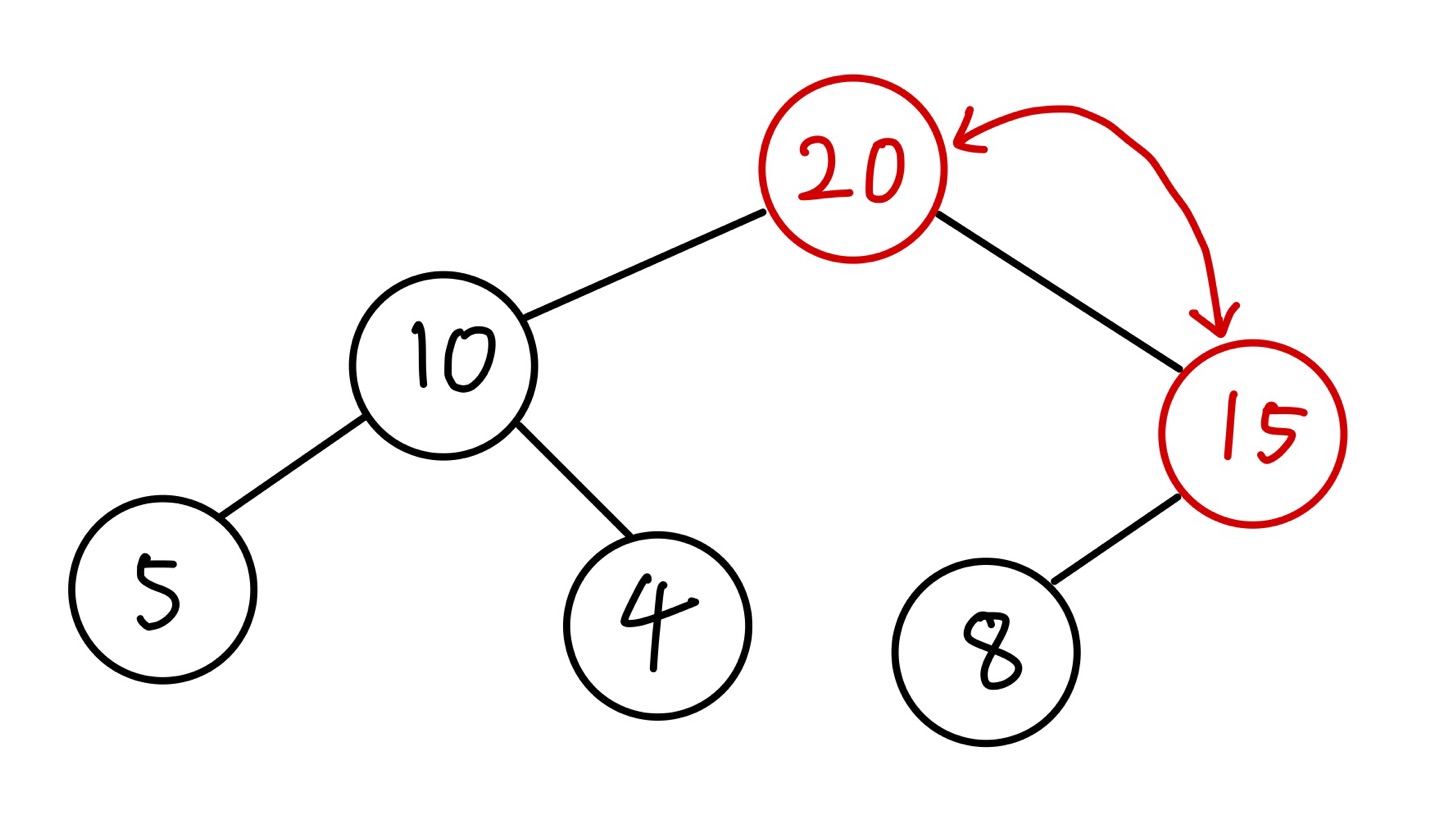
반복이 종료되면 삽입 동작도 종료됩니다.

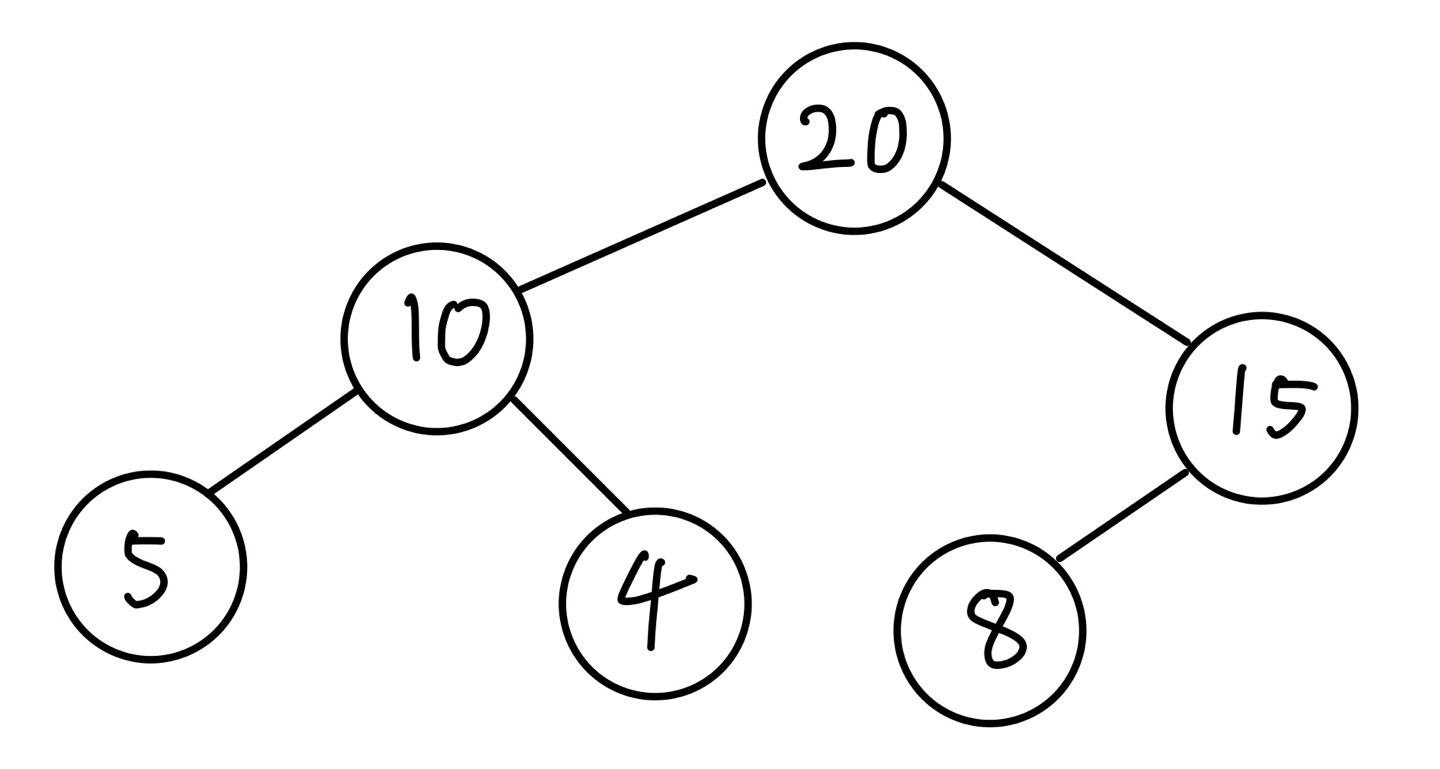
힙의 삭제

다음은 힙의 삭제 동작입니다. 보통 힙에서의 삭제란 루트 노드를 삭제하는 것을 의미합니다. 이는 최대 힙, 최소 힙을 통해 최대값, 최소값을 사용하기 때문입니다. 아래 그림을 예시로 설명하겠습니다.

루트 노드인 값이 20인 노드를 삭제해보겠습니다.

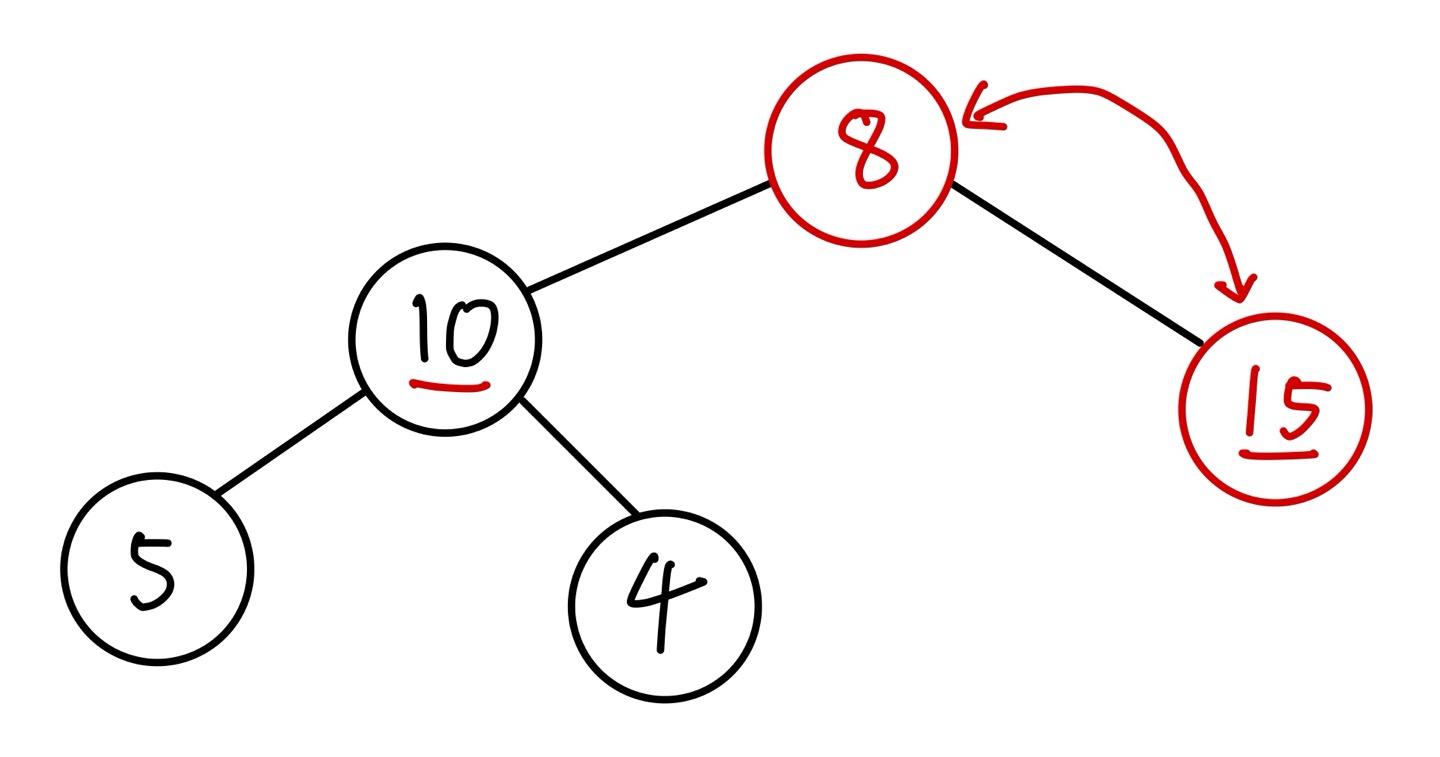
삭제로 인해 비어있는 루트 노드의 자리에 현재 하단, 마지막 자리에 있는 노드(값이 8인 노드)를 위치시킵니다.

그 후, 루트 노드의 값이 자식 노드의 값보다 작다면 두 자식 노드 중 큰 값을 갖고 있는 노드(값이 15인 노드)와 위치를 바꿉니다. 이 동작은 루트 노드로 이동했던 노드(값이 8인 노드)의 값이 자식 노드의 값보다 크거나 자식이 없을 때까지 반복합니다.

📝 파이썬으로 구현

이제 힙을 파이썬을 사용해 구현해보겠습니다. 최대 힙으로 구현해보겠습니다.

일반적으로 힙을 구현할 때 배열 자료구조를 사용합니다. 루트 노드를 배열의 인덱스 번호 1로 정할 수 있습니다. 부모 노드의 인덱스 번호는 자식 노드 인덱스 번호에 몫 연산자( // )를 사용해 구할 수 있습니다. 왼쪽 자식 노드의 인덱스 번호는 부모의 인덱스 번호 * 2를 하고, 오른쪽 자식 노드의 인덱스 번호는 (부모의 인덱스 번호 * 2) + 1을 하면 구할 수 있습니다.

• 부모 인덱스 번호: 자식 인덱스 번호 // 2
• 왼쪽 자식 인덱스 번호: 부모 인덱스 번호 * 2
• 오른쪽 자식 인덱스 번호: (부모 인덱스 번호 * 2) + 1

위 내용을 인지하고 구현을 시작해보겠습니다.

먼저 힙을 생성하겠습니다.

class Heap:
    def __init__(self, root):
        self.max_heap = list()
        self.max_heap.append(None)
        self.max_heap.append(root)
        
    def insert(self, value):
        return
            
    def remove(self):
        return
     
     
 heap = Heap(26)
 
 print(heap.max_heap)  # [None, 26]

다음으로 힙의 삽입 동작의 구현입니다.

class Heap:
    def __init__(self, root):
        self.max_heap = list()
        self.max_heap.append(None)
        self.max_heap.append(root)
        
    def insert(self, value):
        # 새로운 노드를 힙의 마지막에 삽입
        self.max_heap.append(value)
        current_index = len(self.max_heap) - 1
        parent = current_index // 2
        
        # 삽입한 노드의 값이 부모 노드의 값보다 크면 교환
        while current_index > 1 and self.max_heap[current_index] > self.max_heap[parent]:
            self.max_heap[current_index], self.max_heap[parent] = self.max_heap[parent], self.max_heap[current_index]
            current_index = parent
            parent = current_index // 2
            
    def remove(self):
        return
        
heap = Heap(26)
num_list = [7, 12, 54, 97, 21, 91, 27, 57, 96, 69, 61]

for num in num_list:
    heap.insert(num)
    
print(heap.max_heap)  # [None, 97, 96, 91, 54, 69, 61, 21, 7, 27, 26, 57, 12]

마지막으로 삭제 동작입니다.

class Heap:
    def __init__(self, root):
        self.max_heap = list()
        self.max_heap.append(None)
        self.max_heap.append(root)
        
    def insert(self, value):
        # 새로운 노드를 힙의 마지막에 삽입
        self.max_heap.append(value)
        current_index = len(self.max_heap) - 1
        parent = current_index // 2
        
        # 삽입한 노드의 값이 부모 노드의 값보다 크면 교환
        while current_index > 1 and self.max_heap[current_index] > self.max_heap[parent]:
            self.max_heap[current_index], self.max_heap[parent] = self.max_heap[parent], self.max_heap[current_index]
            current_index = parent
            parent = current_index // 2
            
    def remove(self):
        if len(self.max_heap) <= 1:
            print("삭제할 수 없습니다.")
            return
        if len(self.max_heap) == 2:
            root_value = self.max_heap.pop()
            print(f"{root_value}을(를) 삭제했습니다.")
            return 
            
        root_value = self.max_heap[1]
        print(f"{root_value}을(를) 삭제했습니다.")
        self.max_heap[1] = self.max_heap.pop()
        current_index = 1
        
        # 위치를 바꾼 노드외 자식 노드들을 비교
        while True:
            # 왼쪽 자식 노드의 인덱스 번호
            left_index = current_index * 2
            # 오른쪽 자식 노드의 인덱스 번호
            right_index = current_index * 2 + 1
            # 부모 노드와 왼쪽, 오른쪽 자식 노드 중 큰 값을 가진 노드의 인덱스 번호
            largest_index = current_index
            
            # 왼쪽 자식 노드가 존재하고 왼쪽 자식 노드의 값이 부모 노드의 값보다 클 때
            if left_index < len(self.max_heap) and self.max_heap[left_index] > self.max_heap[largest_index]:
                largest_index = left_index
            # 오른쪽 자식 노드가 존재하고 오른쪽 자식 녿의 값이 부모 노드의 값보다 클 때
            if right_index < len(self.max_heap) and self.max_heap[right_index] > self.max_heap[largest_index]:
                largest_index = right_index
            # 부모 노드의 값이 제일 크다면 반복문 종료
            if largest_index == current_index:
                break
                
            # 부모 노드와 큰 값을 가진 노드의 위치를 교환
            self.max_heap[current_index], self.max_heap[largest_index] = self.max_heap[largest_index], self.max_heap[current_index]
            # 위치가 변경된 노드(현재 노드)를 부모 노드로 설정
            current_index = largest_index
            
        return
    
heap = Heap(26)
num_list = [7, 12, 54, 97, 21, 91, 27, 57, 96, 69, 61]

for num in num_list:
    heap.insert(num)
    
print(heap.max_heap)  # [None, 97, 96, 91, 54, 69, 61, 21, 7, 27, 26, 57, 12]

heap.remove()  # 97을(를) 삭제했습니다.

print(heap.max_heap)  # [None, 96, 69, 91, 54, 57, 61, 21, 7, 27, 26, 12]

이상 파이썬으로 구현한 최대 힙이었습니다.

🎁 관련 문제