[자료구조] 파이썬으로 트리 구현하기

LazyMG·2024년 10월 19일
자료구조파이썬
0

자료구조

목록 보기
4/5

🚀 들어가기

드디어 다시 만났습니다. 링크드 리스트 이후 자료구조에서 저를 또다시 힘들게 했던 트리의 등장입니다.

트리의 개념은 정말 단순하죠. 의미는 말 그대로 나무! 모양은 나무를 뒤집은 모양! 하지만 나무라는 생명의 복잡함까지 닮았나 봅니다. 데이터를 추가하고 빼는 과정이 왜이리 복잡할까요. 이번엔 트리를 정복해보려고 합니다. 뿌리부터 잎사귀까지 정복해보겠습니다.

✨ 트리

💡 개념

트리(Tree) 구조란 Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조입니다. 트리 중 이진 트리(Binary Tree) 형태의 구조가 탐색 알고리즘 구현을 위해 많이 사용됩니다.

위 설명에서 Node와 Branch라는 용어가 나왔는데요, 트리에서 사용되는 용어들에 대해 알아보겠습니다. Node(노드) 란 트리에서 데이터를 저장하는 기본 요소입니다. 링크드 리스트에서 사용된 노드와 비슷하게 이해해도 좋습니다. 노드에는 다른 노드와 연결된 정보인 Branch 정보가 포함됩니다.

노드에는 여러 종류가 있는데요, 루트 노드(Root Node)란 트리의 최상위 노드를 말합니다. 단어 그대로 뿌리 노드입니다. 루트 노드 아래의 모든 노드는 루트 노드와 연결됩니다. 다음은 부모 노드(Parent Node)와 자식 노드(Child Node) 입니다. 이 용어는 연결된 두 노드 사이에서 사용됩니다. 두 노드 중 상위 노드를 부모 노드, 하위 노드를 자식 노드라고 합니다. 또 형제 노드(Sibling Node)는 같은 부모 노드를 가진 노드들의 관계를 말합니다. 깊이(Depth, Level)는 루트 노드를 0으로 두고 하위 Branch로 연결된 노드의 깊이를 나타냅니다.

다음은 이진 트리에 대해 알아보겠습니다. 이진 트리는 노드의 Branch가 최대 2인 트리를 말합니다. 모든 노드가 최대 2개의 자식 노드를 가질 수 있는 것이죠. 또 이진 트리 중 부모 노드의 값 보다 작은 노드를 왼쪽에, 부모 노드의 값 보다 큰 노드를 오른쪽에 위치시킨다는 조건이 있는 이진 트리를 이진 탐색 트리(Binary Search Tree)라고 합니다.

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

이진 탐색 트리를 사용하여 데이터를 탐색하면 탐색 속도를 개선할 수 있습니다. 아래 배열과의 탐색 속도 비교를 보시면 이해하기 쉬울 것입니다.

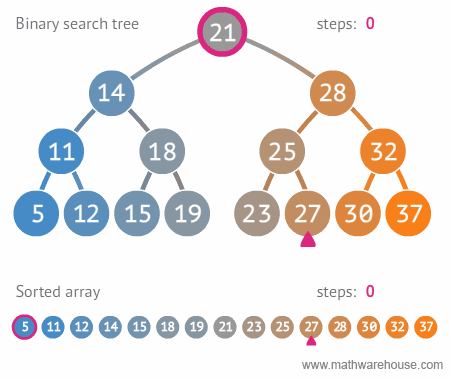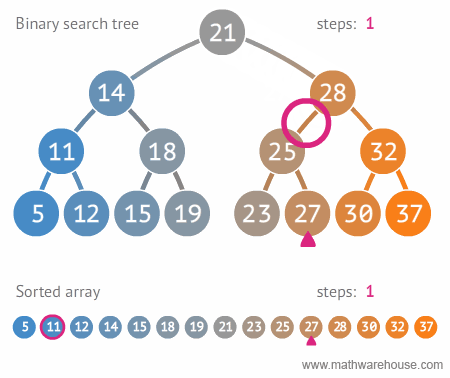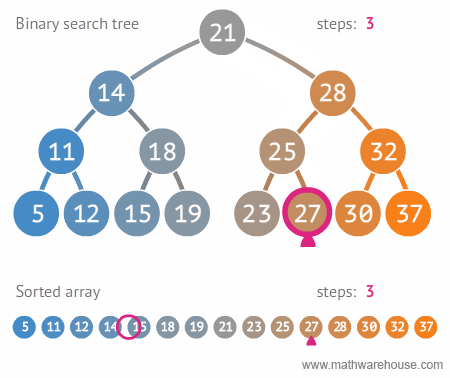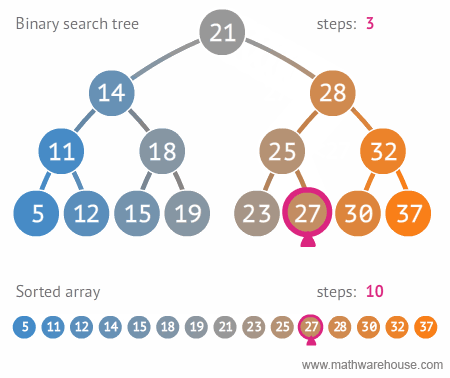
(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

다음은 그림을 통해 이진 탐색 트리의 구조 및 삽입, 삭제, 탐색 동작을 설명해보겠습니다.


📗 설명

⏺️ 이진 탐색 트리

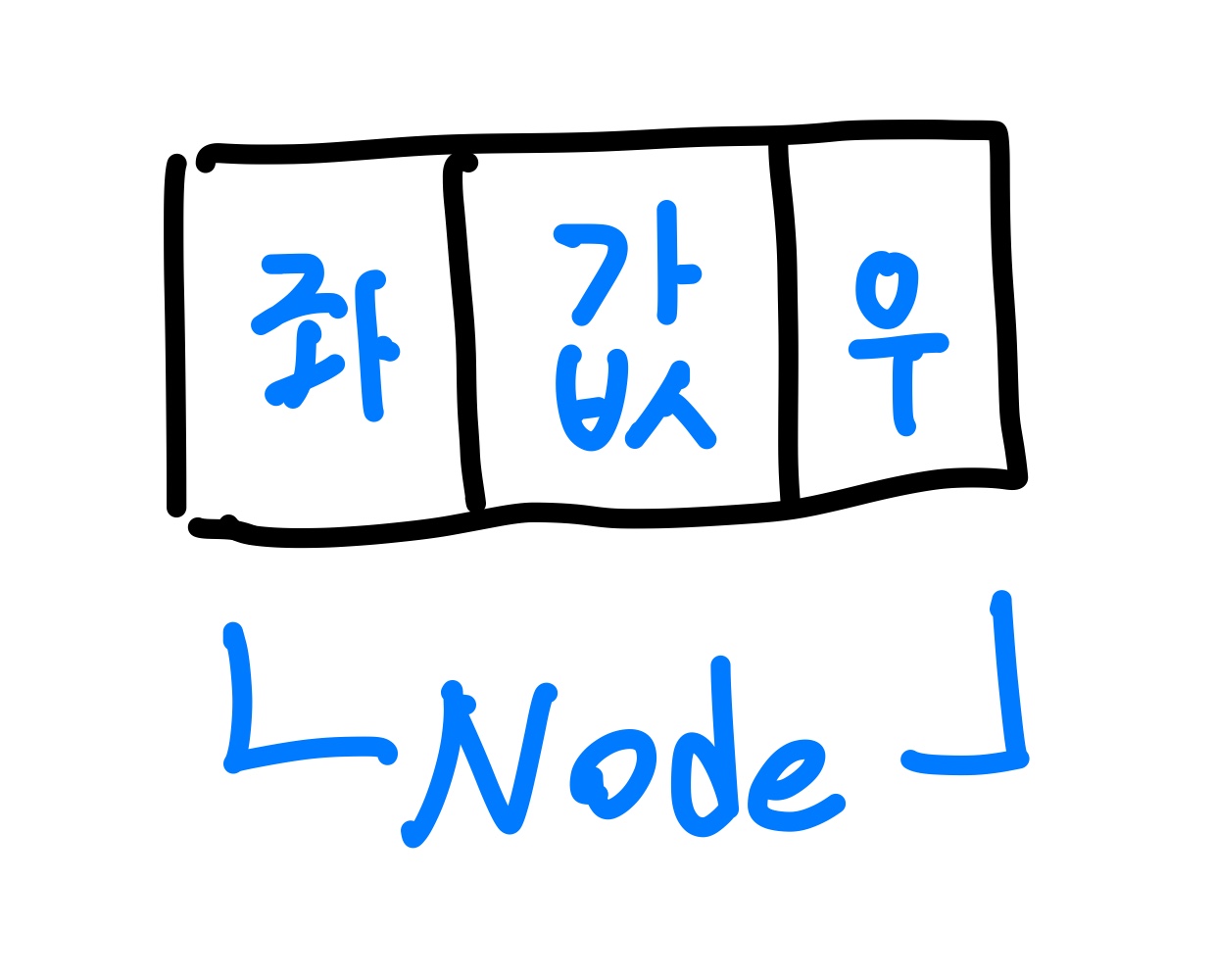
먼저 이진 탐색 트리에서 사용되는 노드입니다. 노드의 값과 좌우의 포인터로 구성되어있습니다. 이 노드는 더블 링크드 리스트에서의 노드와 유사합니다.

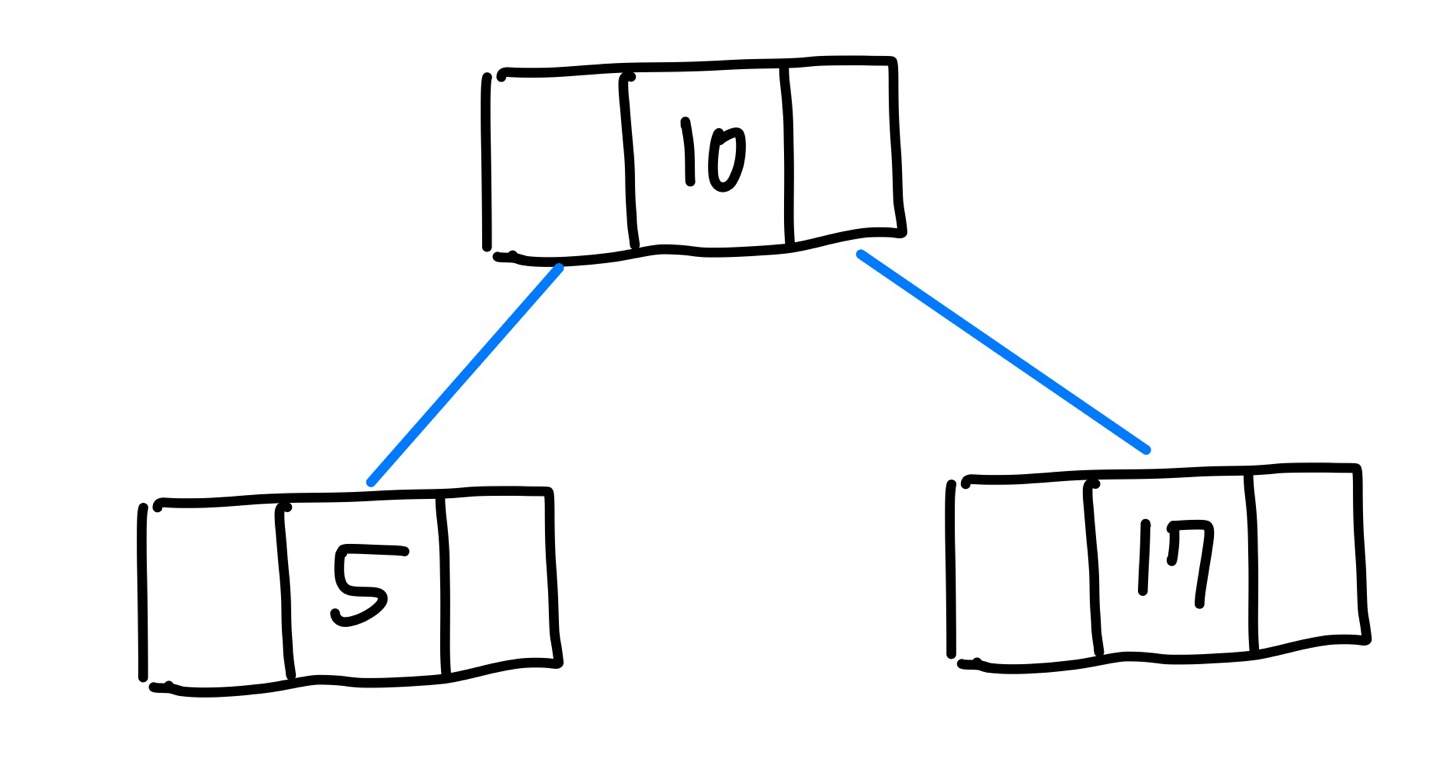
위 노드로 구성된 이진 탐색 트리의 예시입니다. 각 노드의 왼쪽에는 현재 노드의 값보다 작은 값을 가진 노드가 위치하고 오른쪽에는 현재 노드의 값보다 큰 값을 가진 노드가 위치합니다.

⏺️ 이진 탐색 트리의 동작

다음으로 이진 탐색 트리의 동작에 대해 알아보겠습니다. 먼저 삽입 동작입니다.

이진 탐색 트리의 삽입

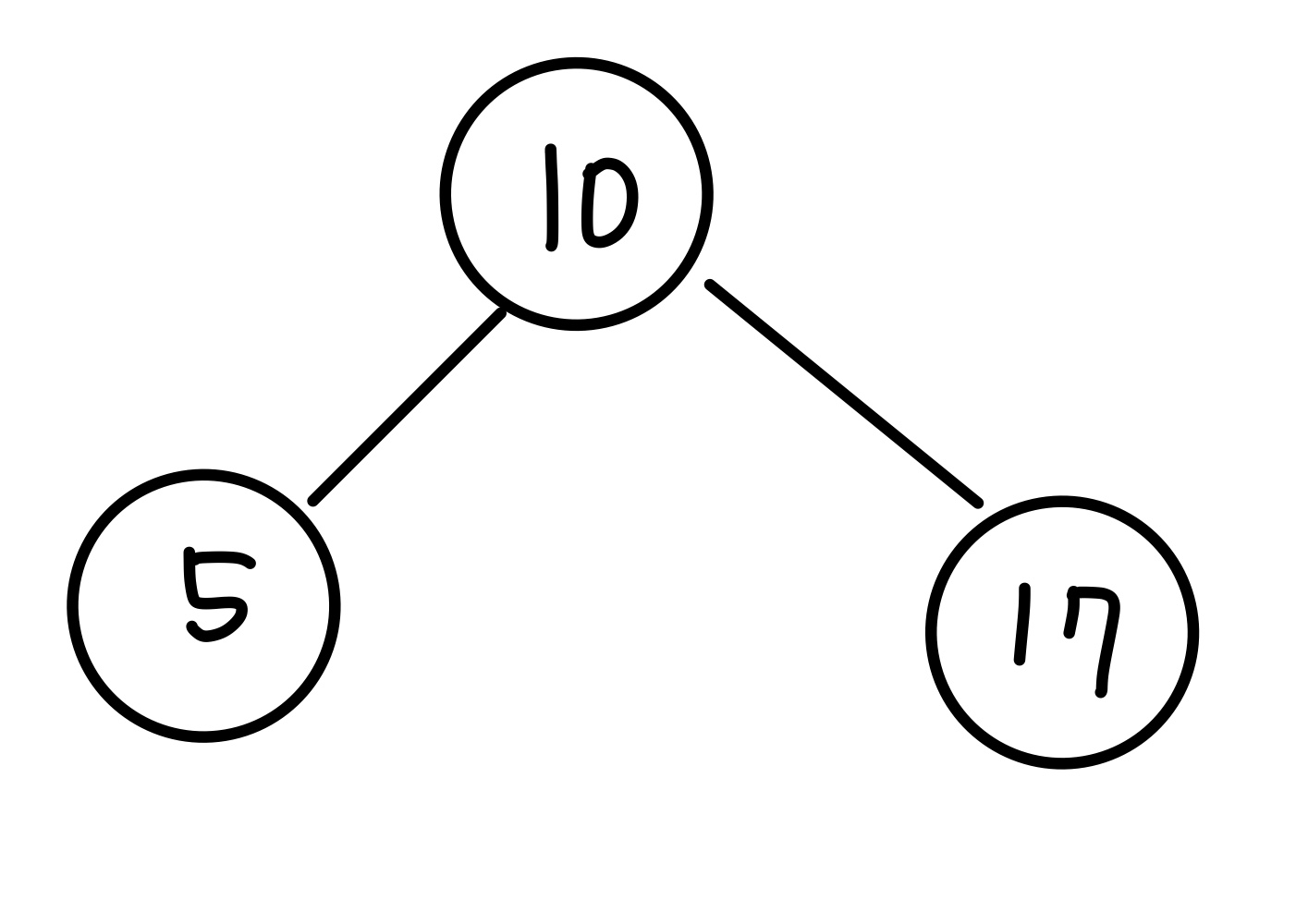
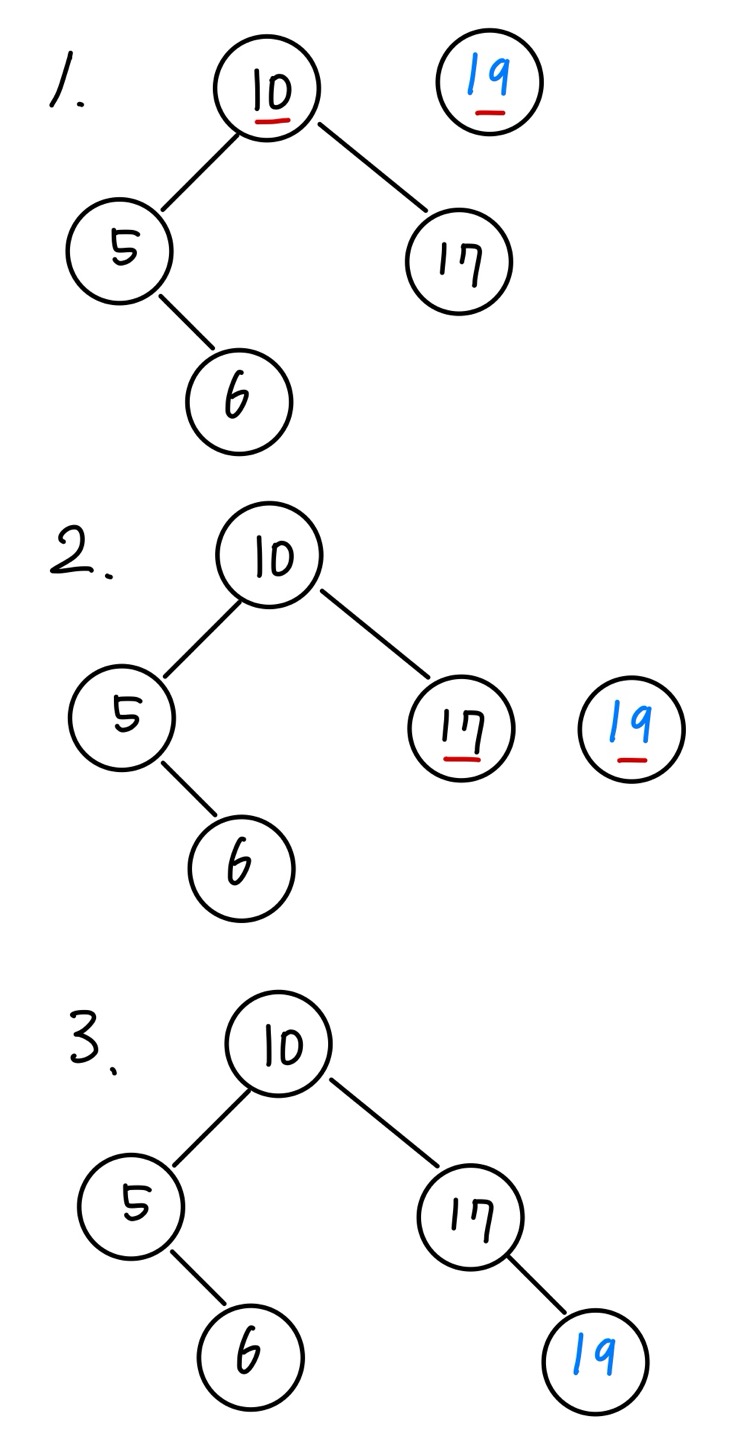
아래 이진 탐색 트리가 주어졌을 때 각각 6, 19, 2의 값을 가진 노드를 순서대로 추가해보겠습니다.

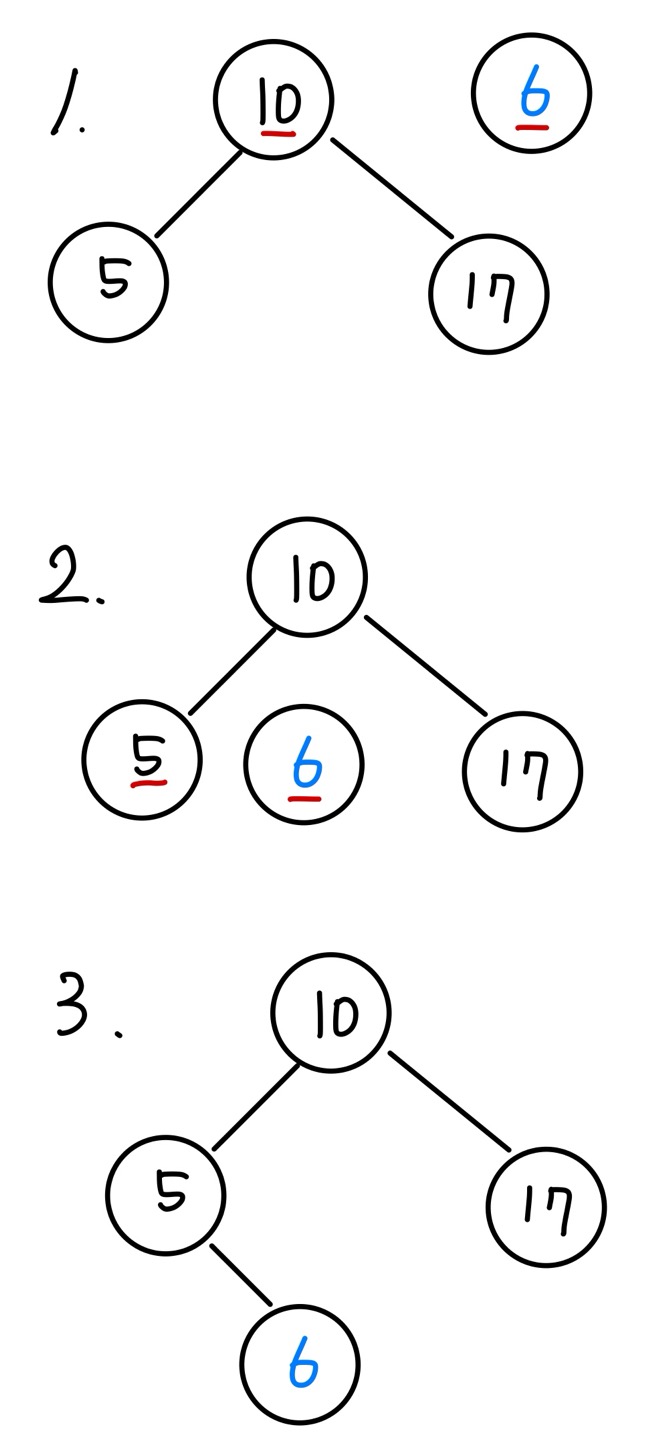
값이 6인 노드의 삽입 과정입니다. 먼저 현재 노드를 루트 노드로 설정합니다. 현재 노드의 값인 10과 값을 비교합니다. 6이 10보다 작기 때문에 현재 노드의 왼쪽으로 이동합니다.
현재 노드의 왼쪽 포인터가 이미 노드를 가리키고 있기 때문에 현재 노드가 가리키고 있는 노드와 값을 비교해야 합니다. 현재 노드를 이동해 비교합니다.
6이 현재 노드의 값인 5보다 크기 때문에 현재 노드의 오른쪽으로 이동합니다. 현재 노드의 오른쪽 포인터가 가리키는 값이 없기 때문에 값이 6인 노드를 현재 노드의 오른쪽 포인터가 가리키도록 하면 삽입 동작이 완료됩니다.

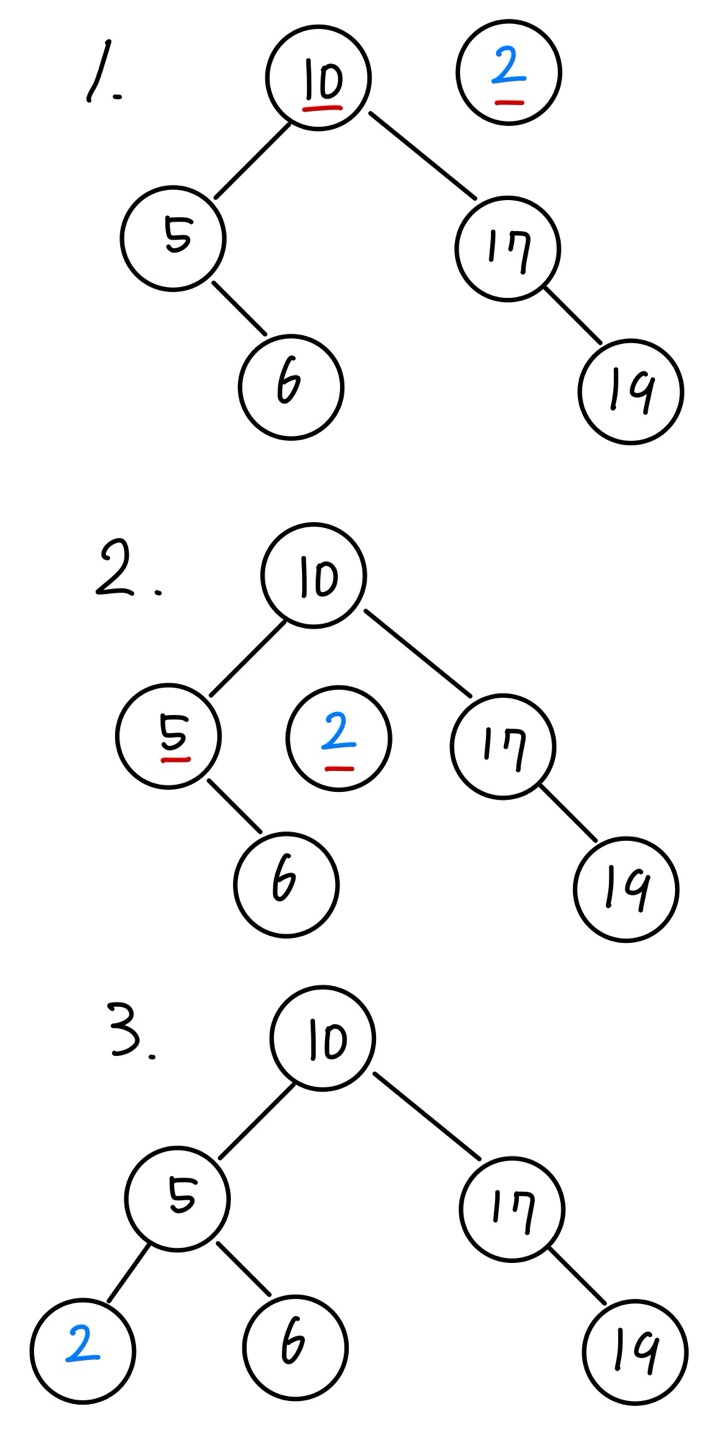
값이 19와 2인 노드의 삽입 동작 과정은 아래와 같습니다. 방식은 동일합니다.

이진 탐색 트리의 탐색

이진 탐색 트리의 탐색은 어떤 값을 가진 노드가 현재 이진 탐색 트리에 존재하는지 확인하는 동작입니다.

아래 이진 탐색 트리에서 동작을 확인하겠습니다.

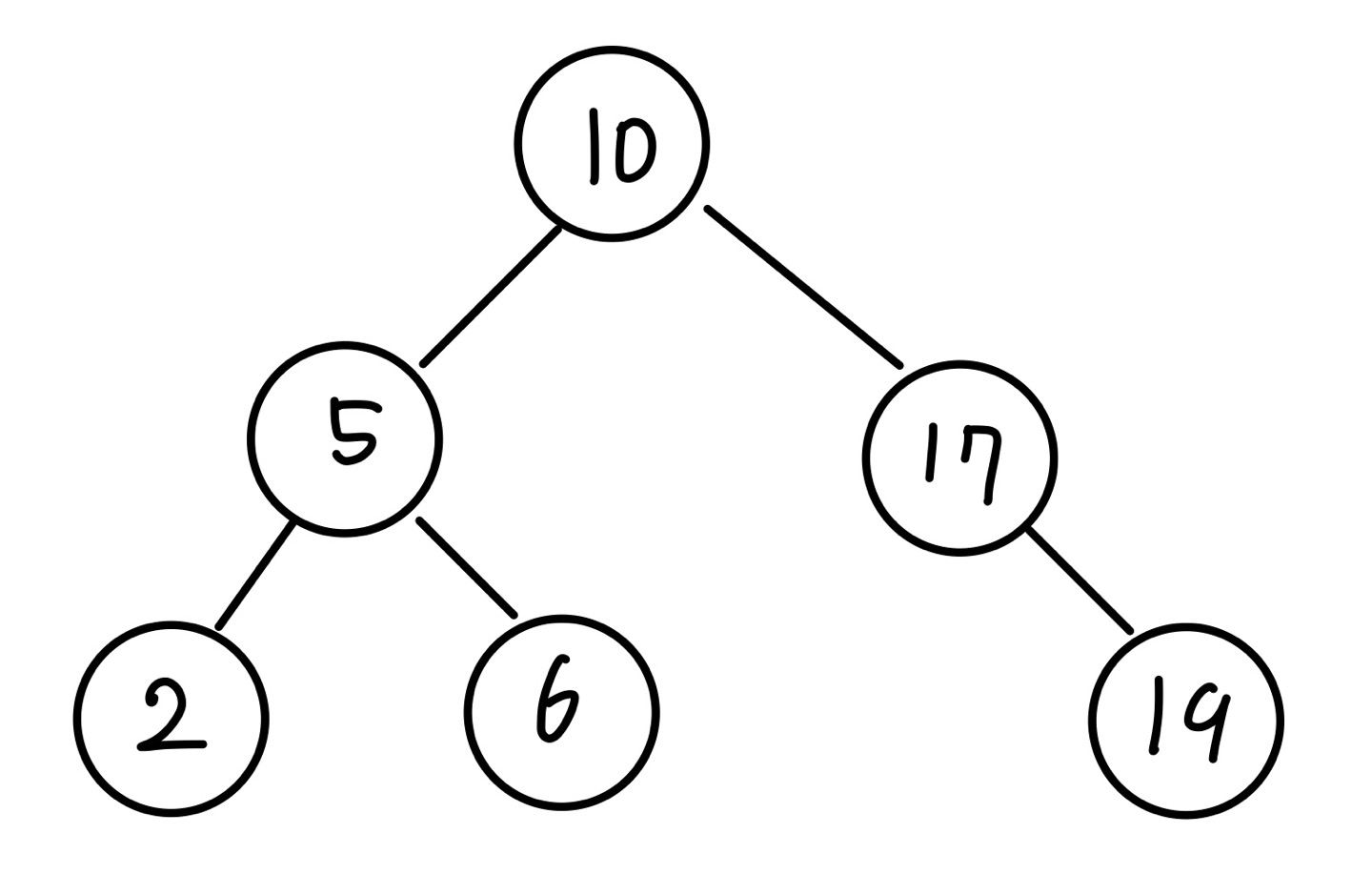
값이 6인 노드를 찾아보겠습니다. 먼저 현재 노드를 루트 노드로 설정합니다. 6이 현재 노드의 값인 10보다 작기 때문에 현재 노드의 왼쪽으로 이동해야 합니다. 현재 노드의 왼쪽 포인터가 가리키는 노드가 존재하기 때문에 현재 노드를 현재 노드의 왼쪽 노드로 설정합니다.
현재 노드의 값이 5이고 6이 5보다 크기 때문에 현재 노드의 오른쪽 노드로 이동해야 합니다. 현재 노드의 오른쪽 포인터가 가리키는 노드가 존재하므로 현재 노드를 현재 노드의 오른쪽 노드로 설정합니다.
현재 노드의 값이 6이고 찾으려는 노드의 값, 6과 같기 때문에 현재 이진 탐색 트리에서의 탐색은 성공으로 종료됩니다.

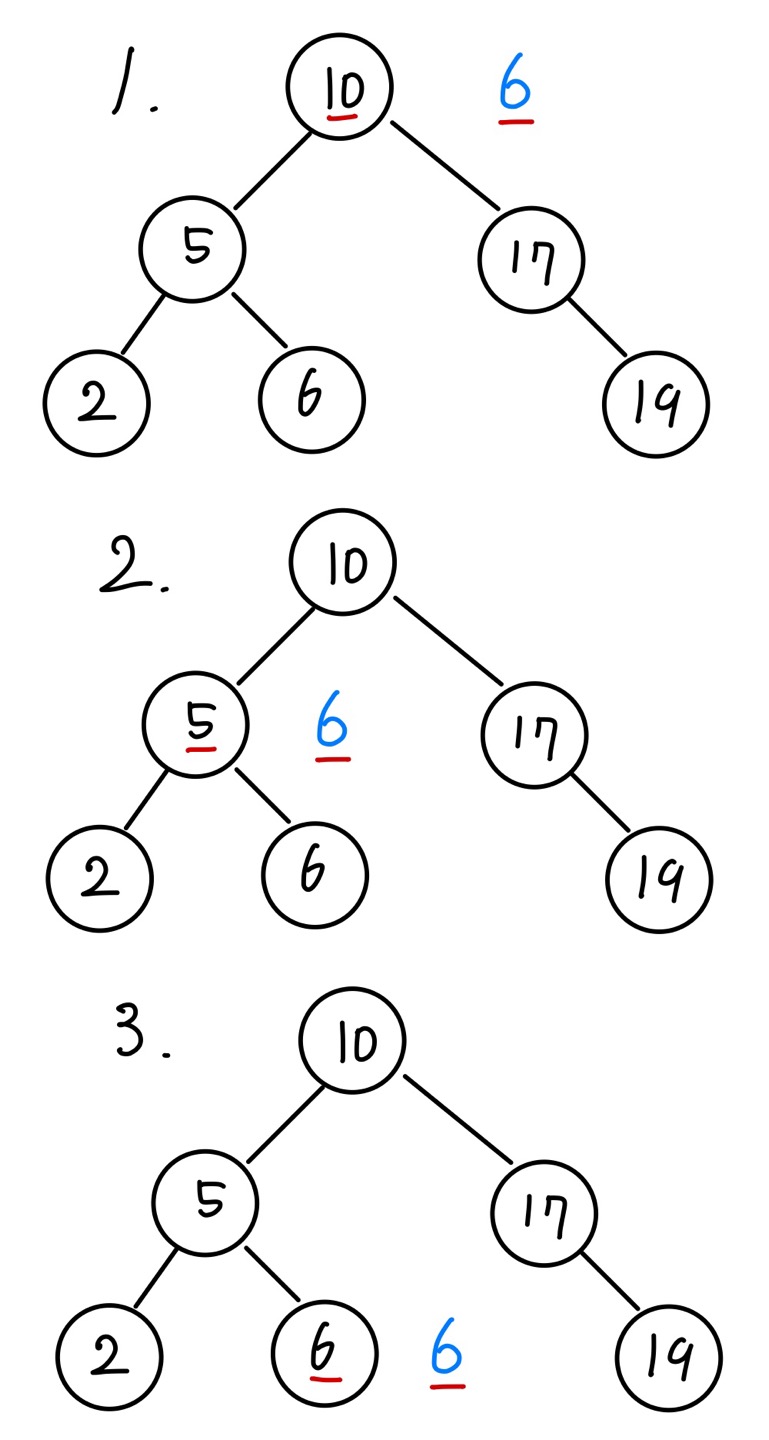
현재 이진 트리 탐색에 존재하지 않는 노드를 찾아보겠습니다. 값이 11인 노드를 찾아보겠습니다. 위와 동일하게 동작하므로 현재 노드의 값이 17인 상황으로 넘어가겠습니다. 11이 현재 노드의 값인 17보다 작기 때문에 현재 노드의 왼쪽으로 이동해야 합니다. 하지만 현재 노드의 왼쪽 포인터가 가리키는 노드가 없으므로 이동할 수 없습니다. 이때 현재 이진 탐색 트리에 값이 11인 노드가 없다고 판단하여 실패로 탐색을 종료합니다.

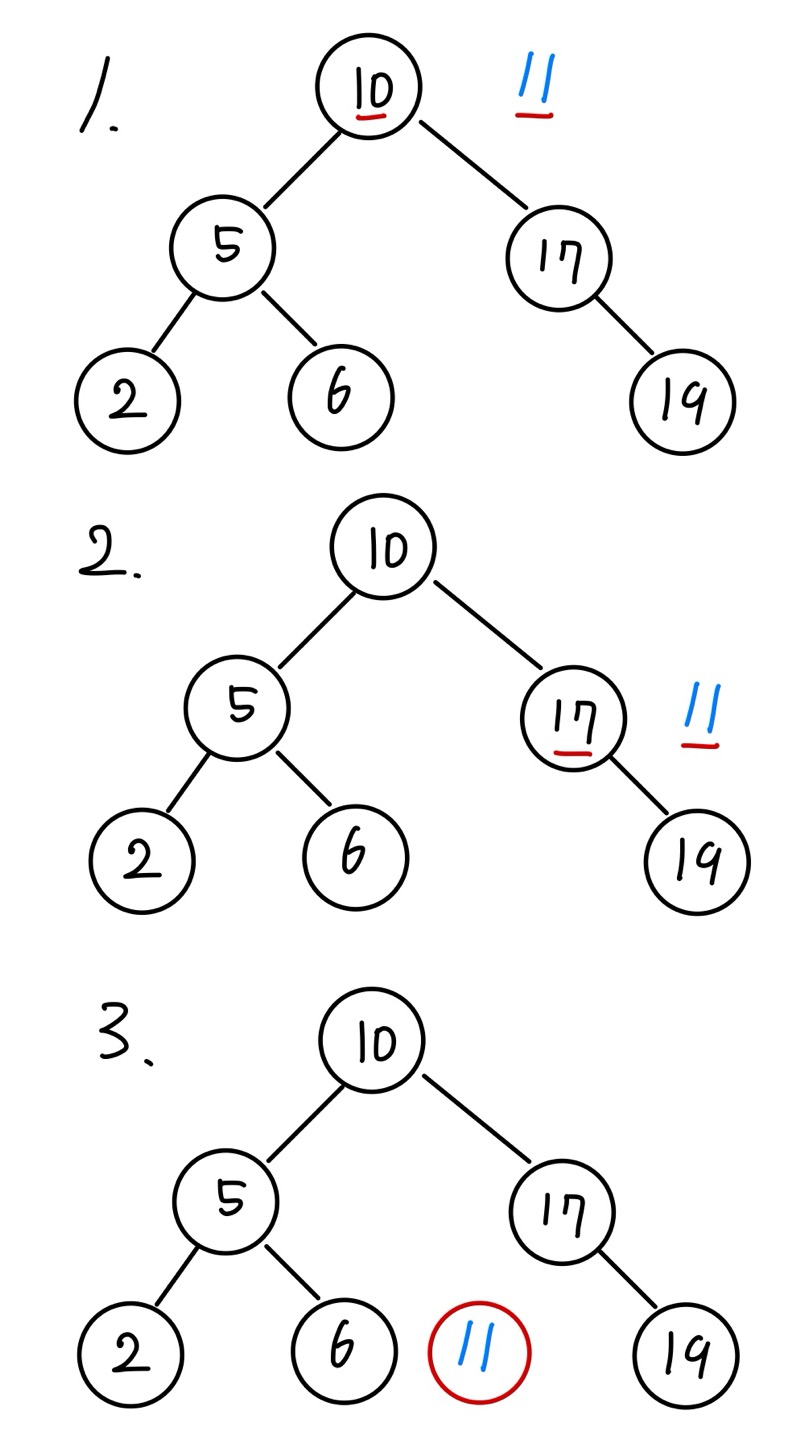
이진 탐색 트리의 삭제

다음은 이진 탐색 트리에서의 삭제인데요, 삭제 동작은 경우를 나누어서 알아보겠습니다.

  • 자식 노드가 존재하지 않는 Leaf Node일 경우
  • 자식 노드가 하나 존재하는 노드일 경우
  • 자식 노드가 두 개 존재하는 노드일 경우

아래 이진 탐색 트리를 기준으로 알아보겠습니다.

먼저 삭제하고자 하는 값의 노드로 이동해야 합니다. 해당 과정은 탐색 동작과 동일하기 때문에 아래 설명에서는 생략하겠습니다. 존재하지 않는 값의 노드를 삭제하고자 하면 탐색 동작을 통해 확인한 후 오류를 알리면 됩니다.

자식 노드가 존재하지 않는 Leaf Node일 경우
값이 2인 노드를 삭제해보겠습니다. 현재 노드의 값이 2이고 부모 노드의 값이 5입니다.

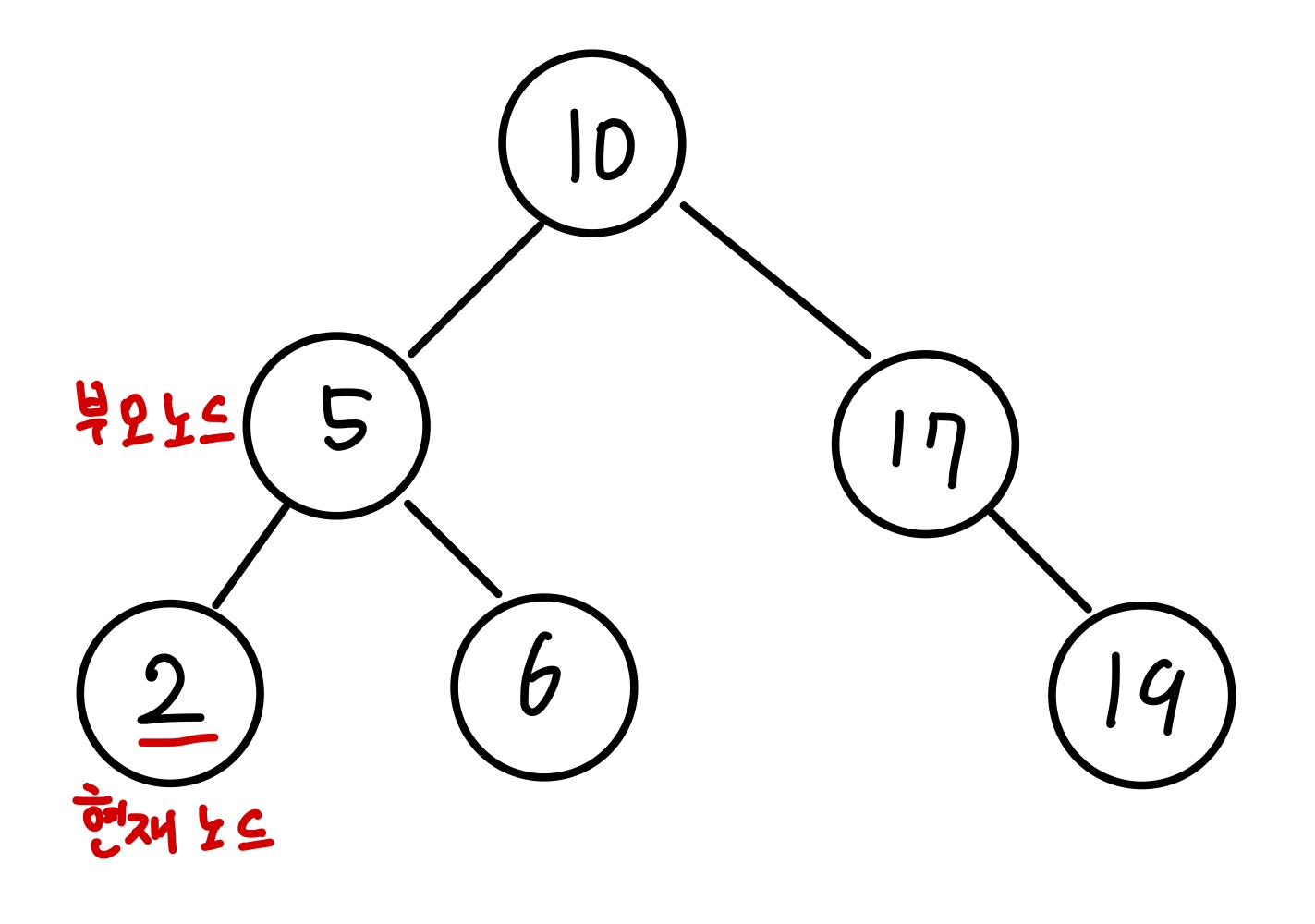
현재 노드를 부모 노드의 왼쪽 포인터가 가리키고 있으므로 부모 노드의 왼쪽 포인터가 아무 노드도 가리키지 않도록 합니다. 그 다음 현재 노드를 삭제하면 Leaf Node의 삭제가 완료됩니다.

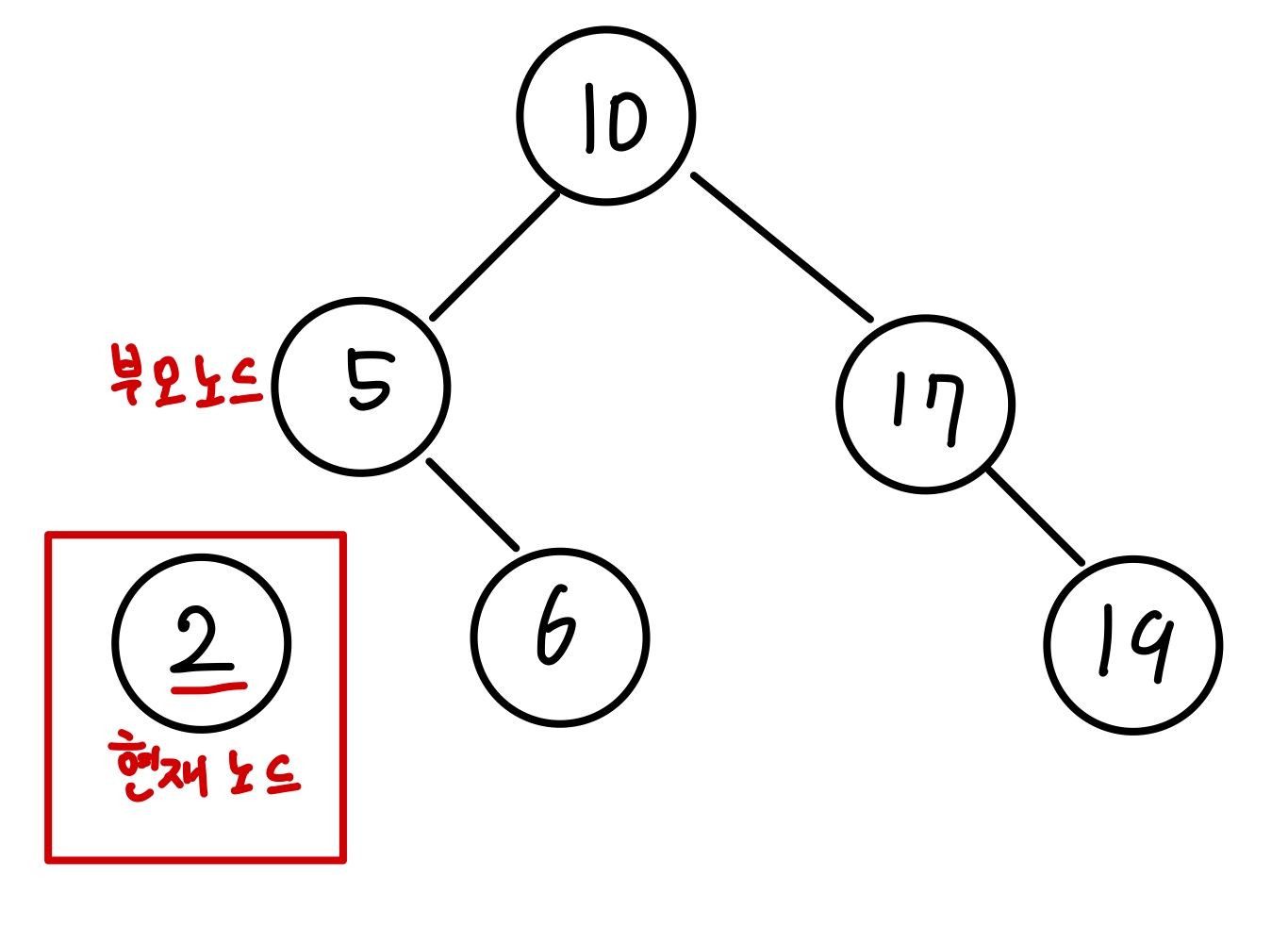
자식 노드가 하나 존재하는 노드일 경우
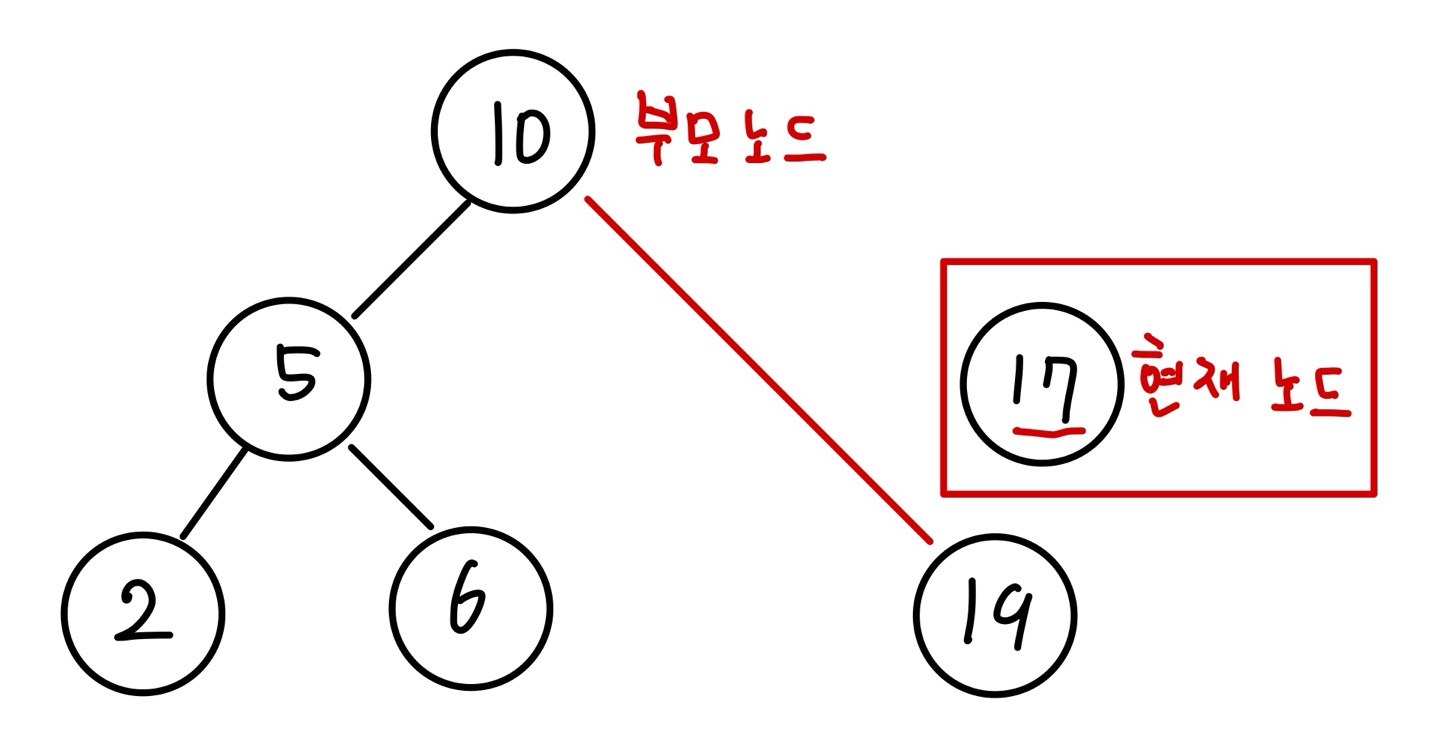
값이 17인 노드를 삭제해보겠습니다. 현재 노드의 값이 17이고 부모 노드의 값이 10입니다.

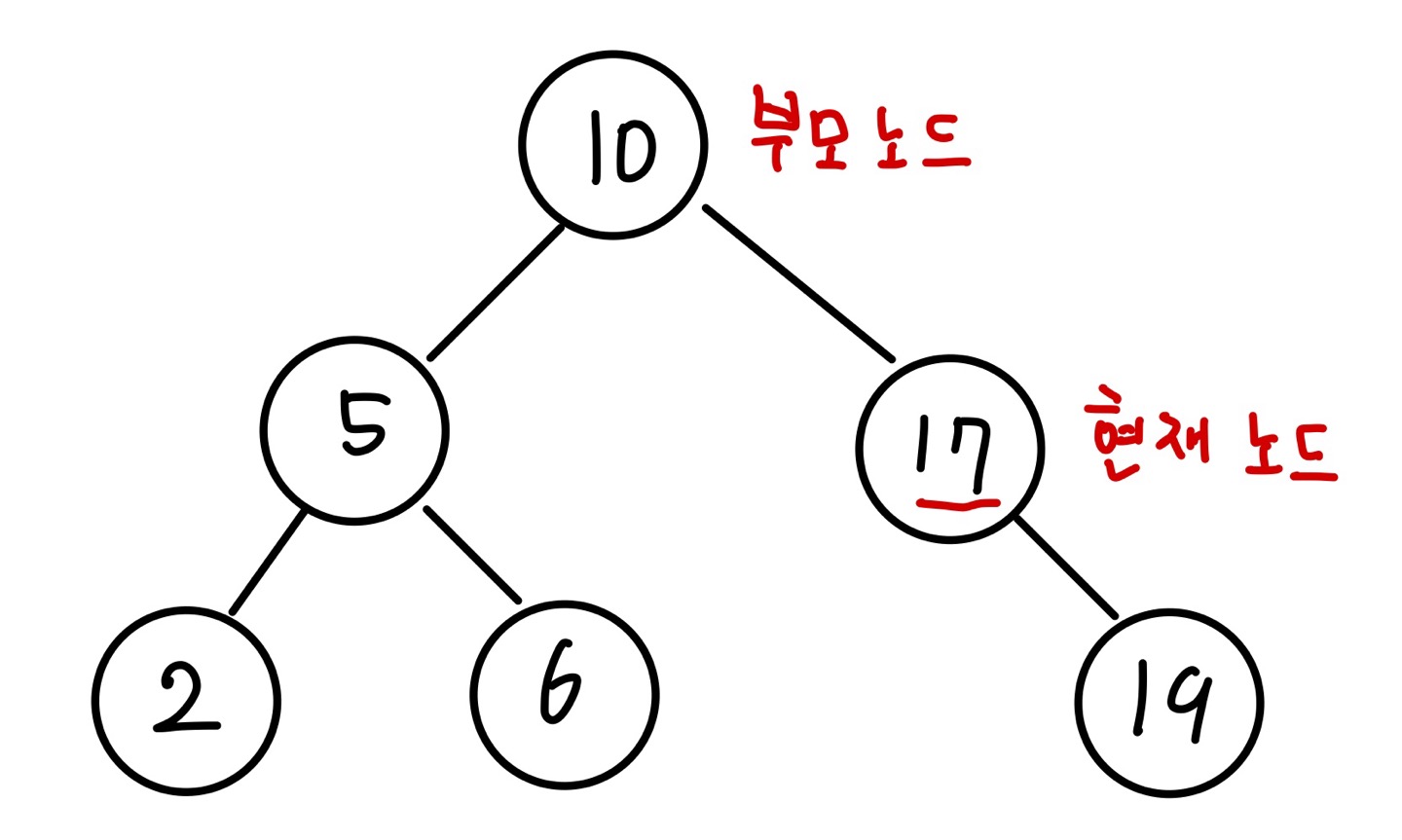
먼저 현재 노드의 자식 노드를 현재 노드의 왼쪽, 오른쪽 포인터 중 어떤 포인터가 가리키고 있는지 확인합니다. 해당 예시에서는 오른쪽 노드가 가리키고 있습니다. 또 현재 노드를 가리키고 있는 부모 노드의 포인터를 확인합니다. 해당 예시에서는 부모 노드의 오른쪽 포인터가 현재 노드를 가리키고 있습니다. 그럼 부모 노드의 오른쪽 노드가 현재 노드의 오른쪽 포인터가 가리키는 노드를 가리키도록 합니다. 그 다음 현재 노드를 삭제하면 자식 노드가 하나 존재하는 노드의 삭제 동작이 완료됩니다.

자식 노드가 두 개 존재하는 노드일 경우
자식 노드가 두 개 존재하는 노드일 경우, 다시 두 가지 경우로 나눌 수 있습니다.

  • 삭제하려는 노드가 부모 노드의 왼쪽에 있을 경우
  • 삭제하려는 노드가 부모 노드의 오른쪽에 있을 경우

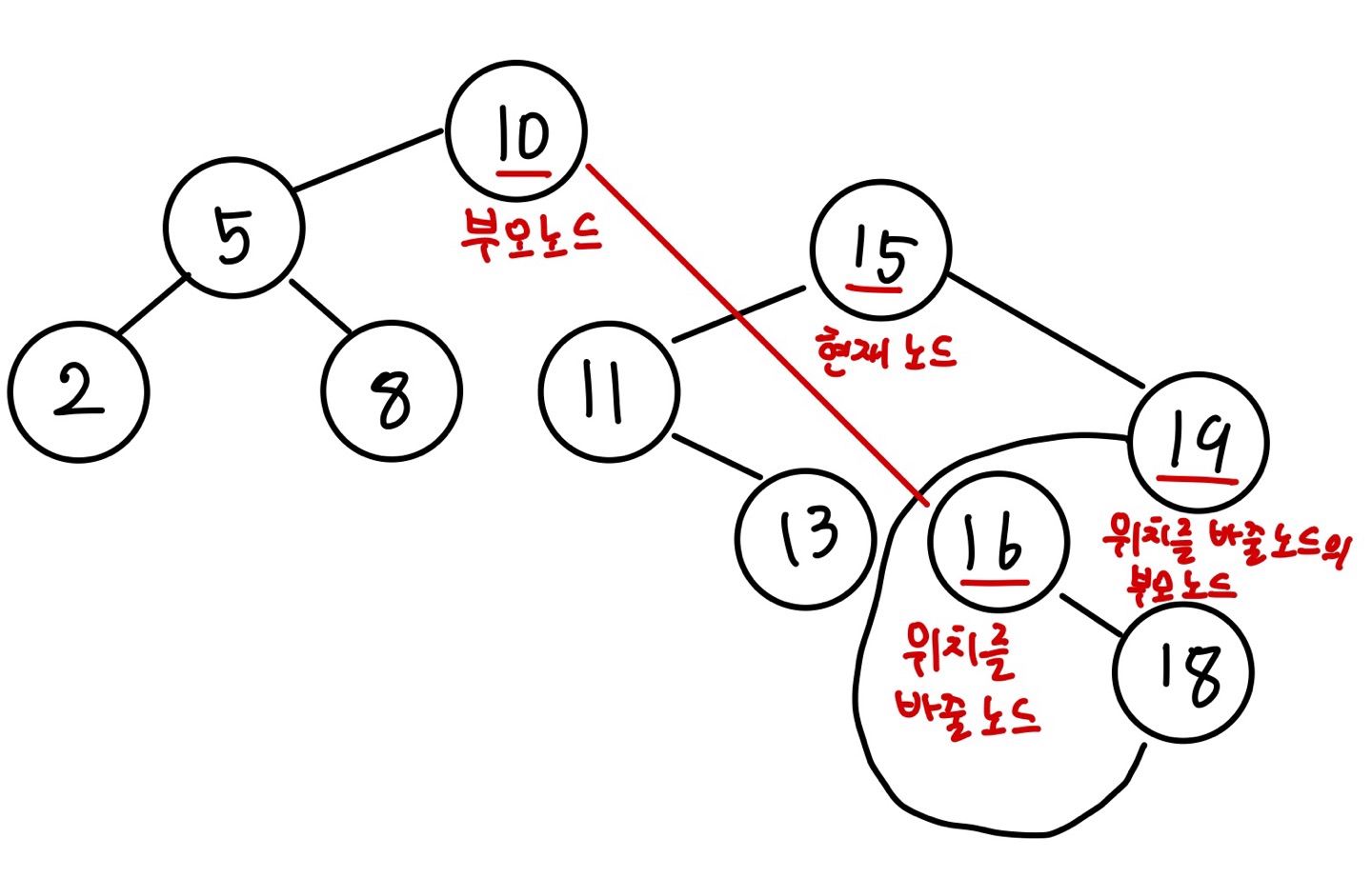
먼저 삭제하려는 노드가 부모 노드의 왼쪽에 있을 경우입니다. 복잡한 동작을 확인하기 위해서 다음 이진 탐색 트리를 예시로 사용하겠습니다.

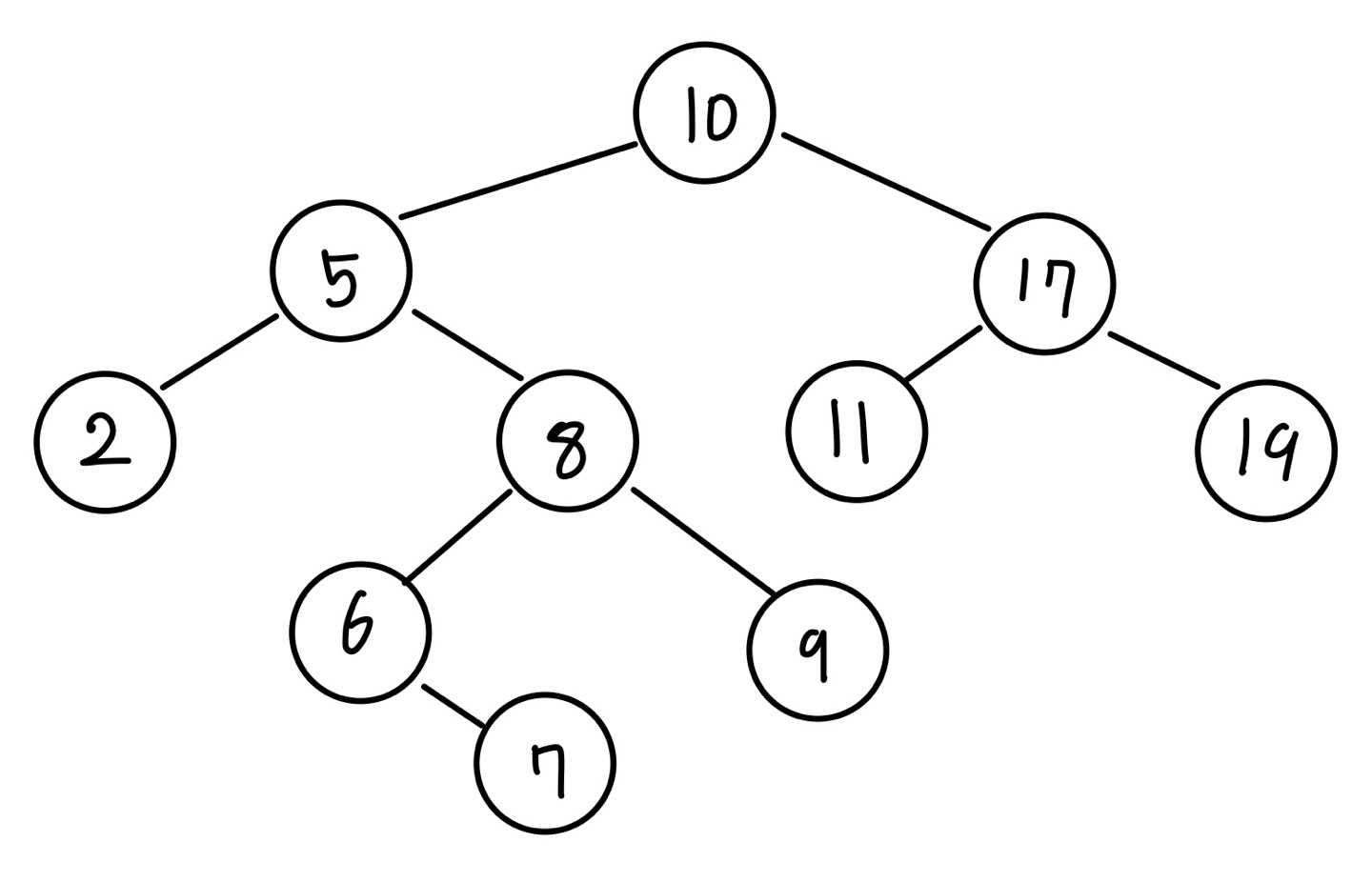
현재 노드가 삭제하려는 노드(값이 5인 노드)인 상태입니다.

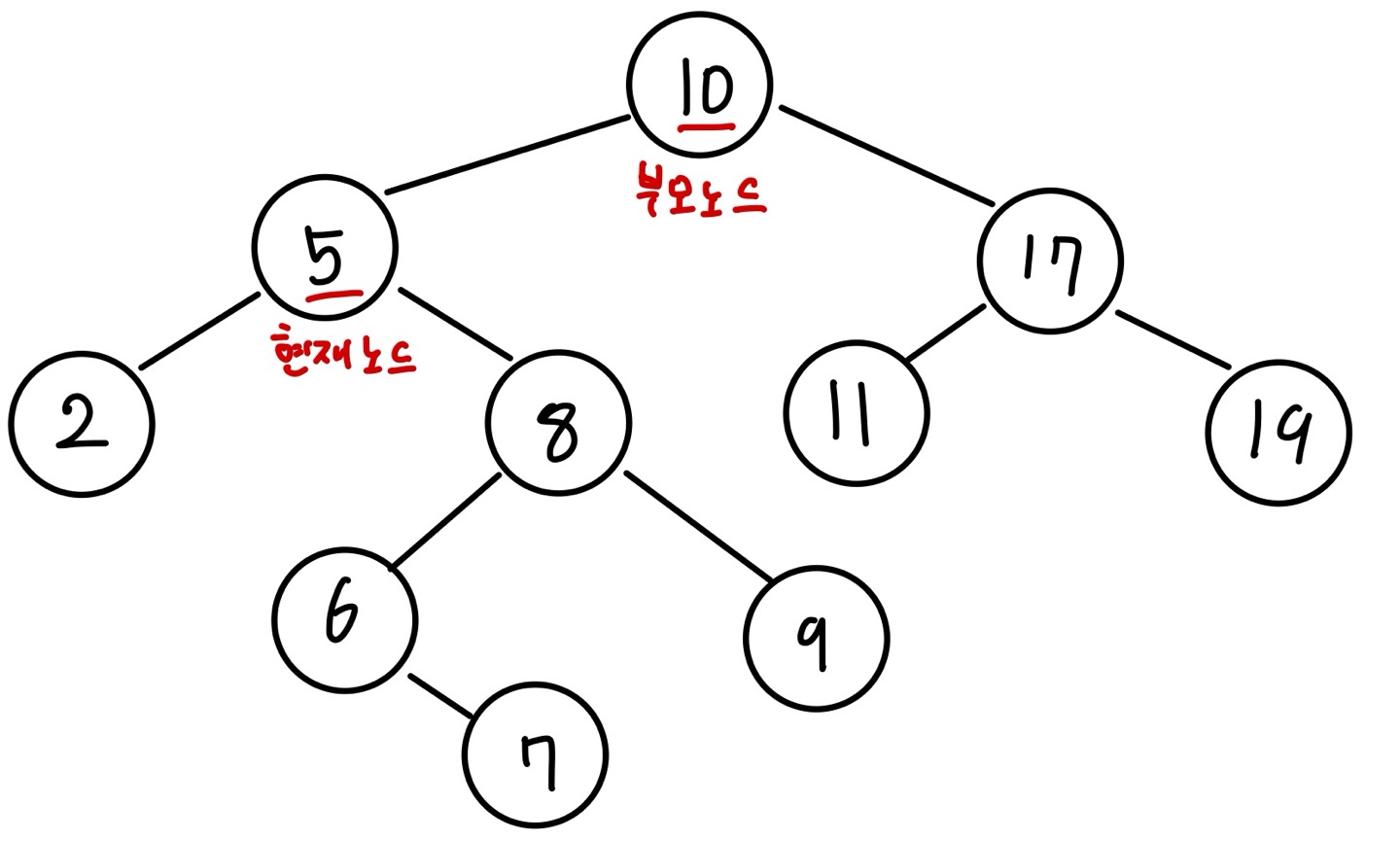
현재 노드를 삭제하려면 부모 노드(값이 10인 노드)의 왼쪽 포인터가 가리킬 노드를 정해야 합니다. 이때 현재 노드의 오른쪽에 있는 노드 중 가장 작은 값을 가진 노드(값이 6인 노드)를 가리키도록 하겠습니다. 즉, 노드의 위치를 이동하는 것입니다. 이 과정을 진행할 때 위치를 바꿀 노드의 자식 노드 또한 고려해야 합니다. 다만 위치를 바꿀 노드의 자식 노드가 있다면 오른쪽에만 위치할 것입니다. 위치를 바꿀 노드는 현재 노드의 오른쪽 노드 중 가장 작은 값이기 때문에 해당 노드보다 작은 값을 가진 노드는 없습니다.

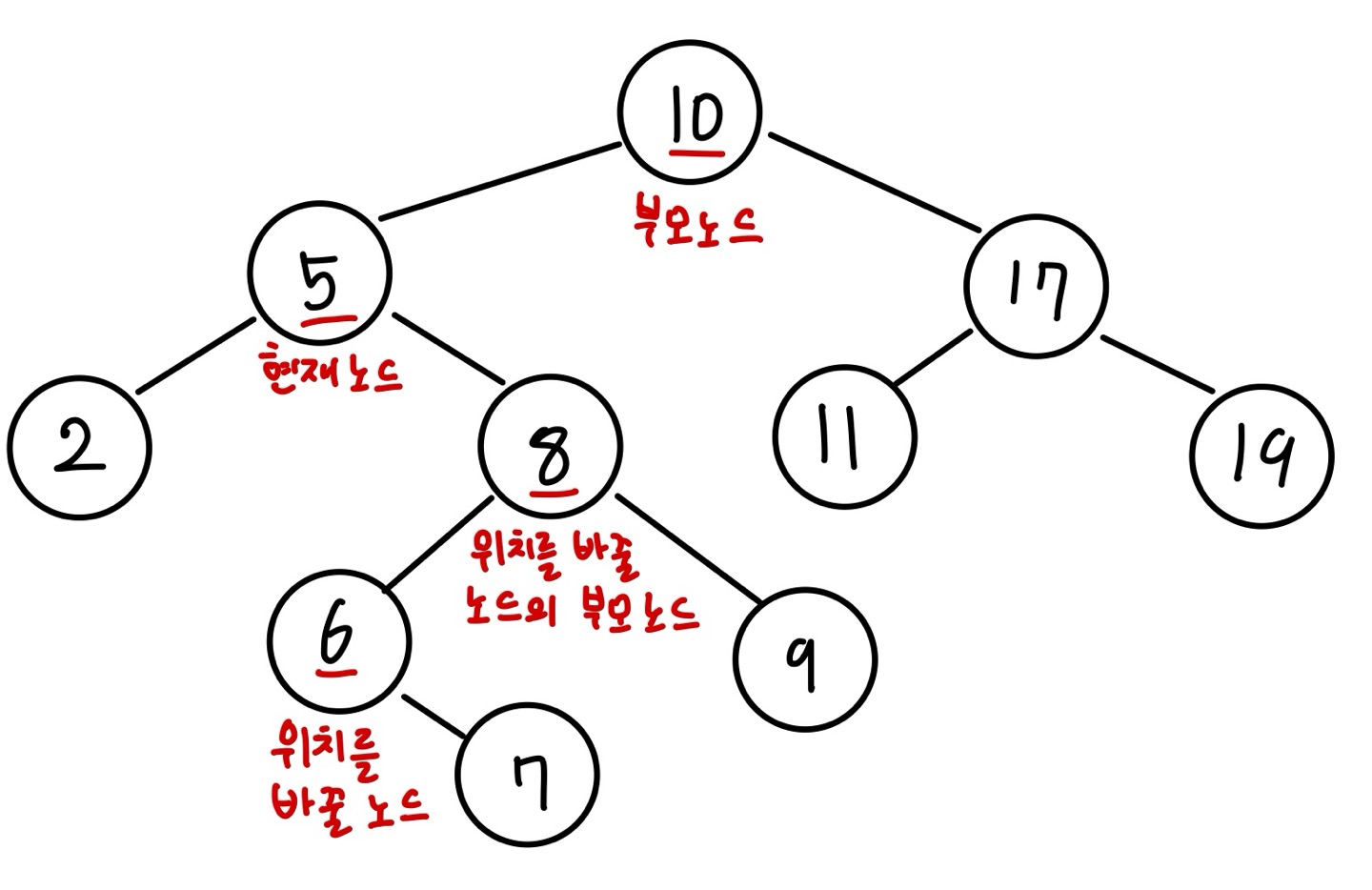
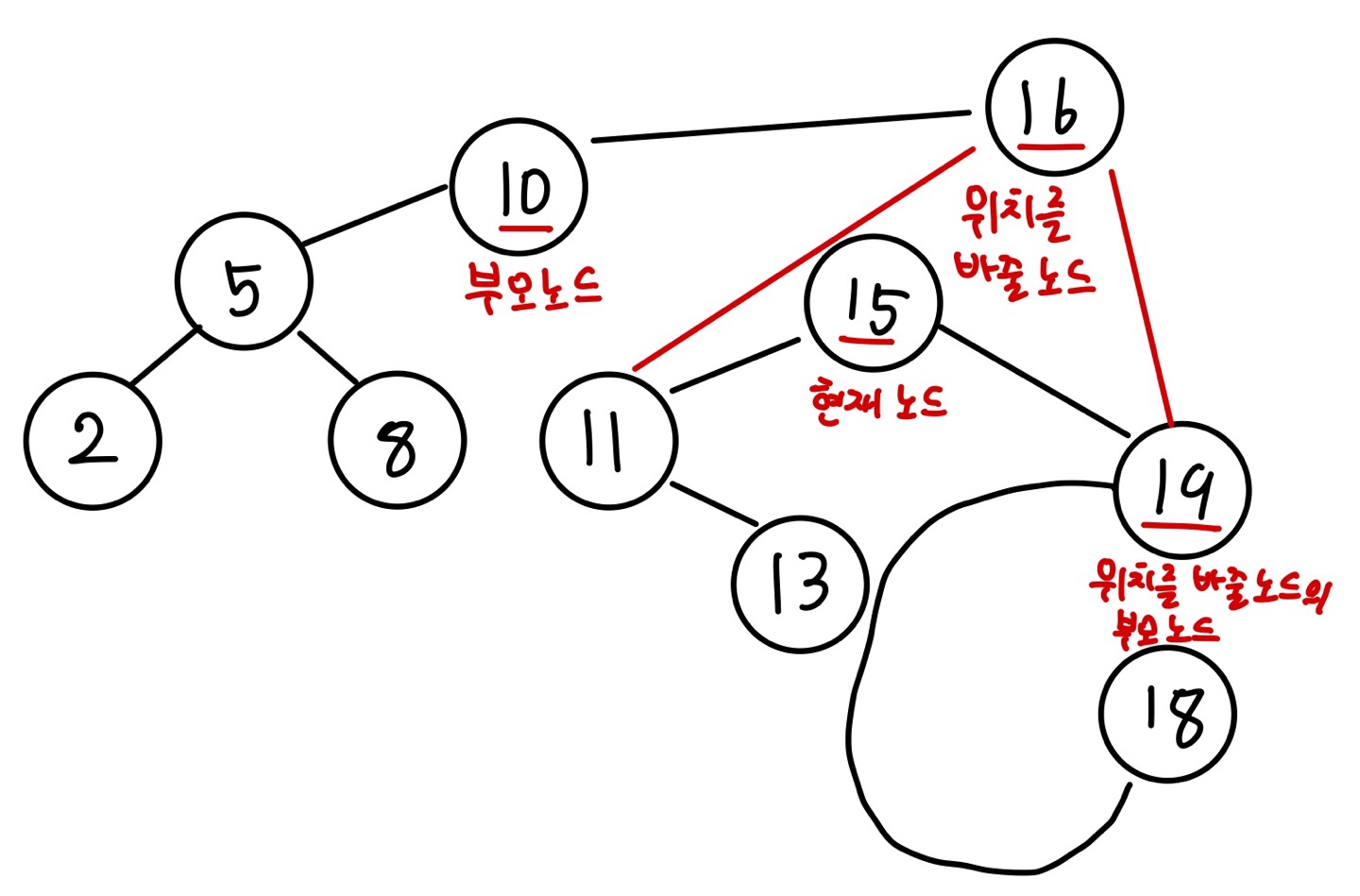
위치를 바꿀 노드(값이 6인 노드)의 오른쪽 포인터가 가리키는 노드가 있다면 위치를 바꿀 노드의 부모 노드(값이 8인 노드)의 왼쪽 포인터가 위치를 바꿀 노드의 오른쪽 포인터가 가리키는 노드(값이 7인 노드)를 가리키도록 설정합니다.

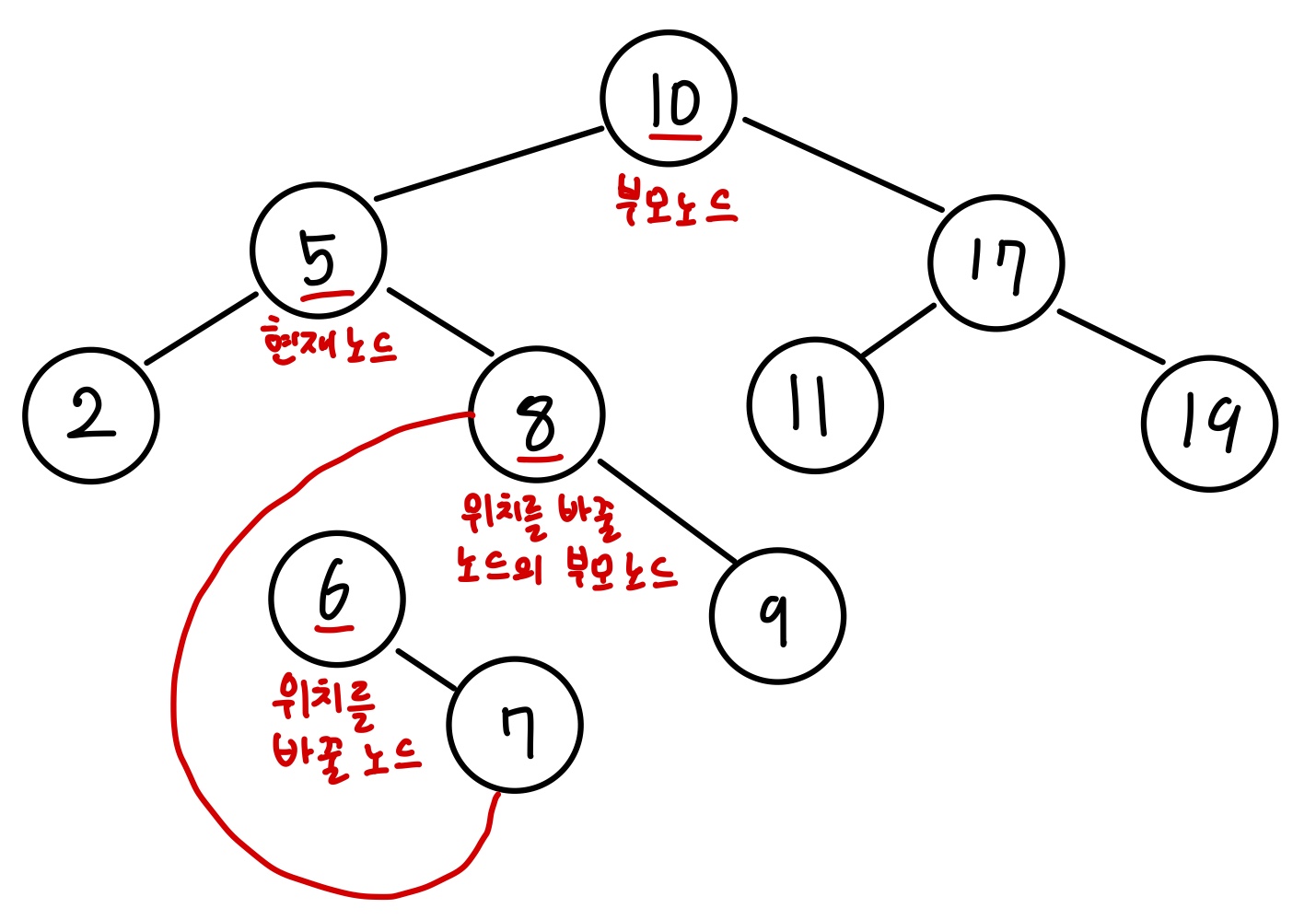
부모 노드(값이 10인 노드)의 왼쪽 포인터가 위치를 바꿀 노드(값이 6인 노드)를 가리키도록 합니다.

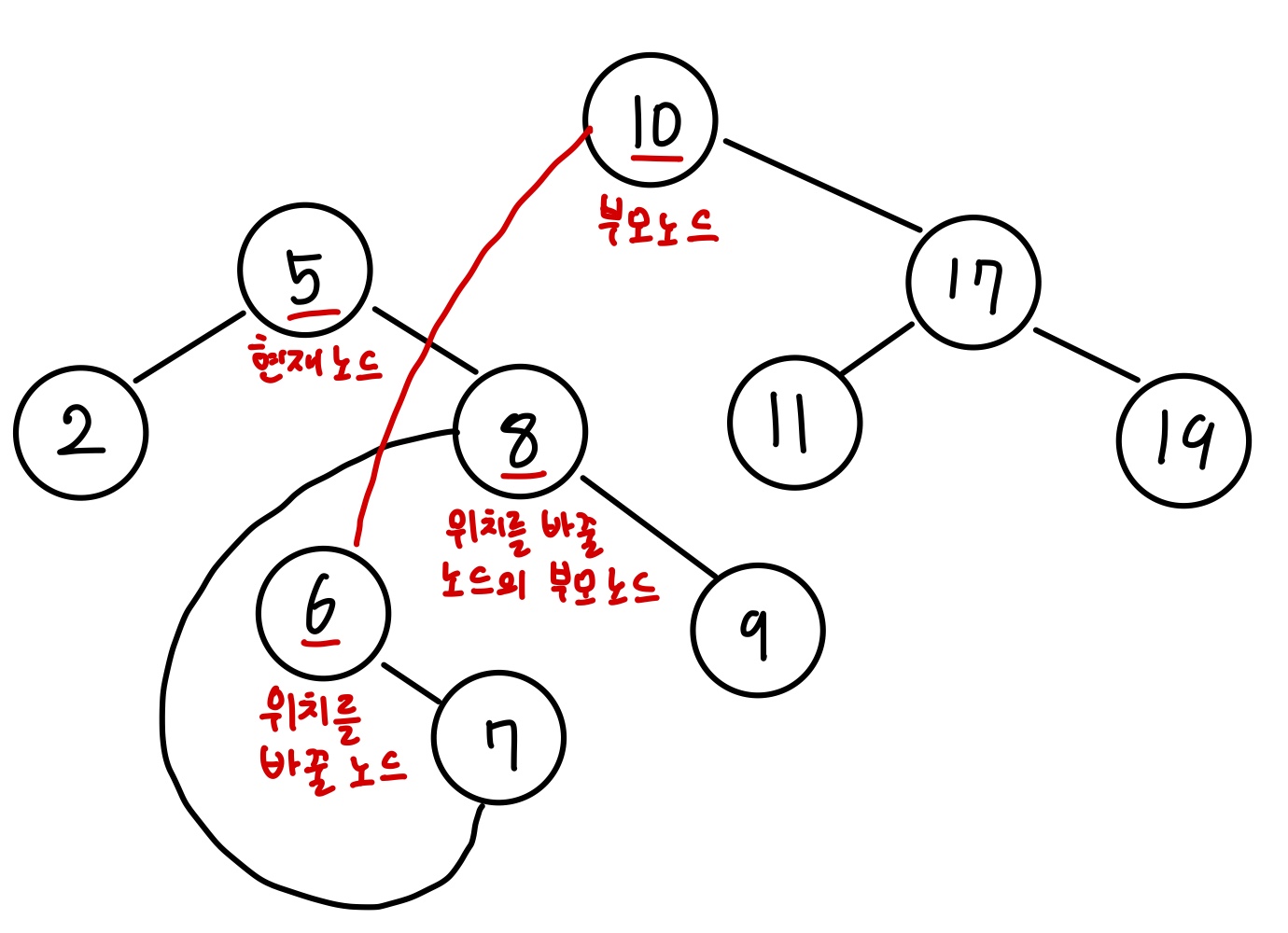
그 다음 현재 노드(값이 5인 노드)의 왼쪽, 오른쪽 포인터가 가리키는 노드를 각각 위치를 바꿀 노드(값이 6인 노드)의 왼쪽, 오른쪽 포인터가 가리키도록 설정합니다.

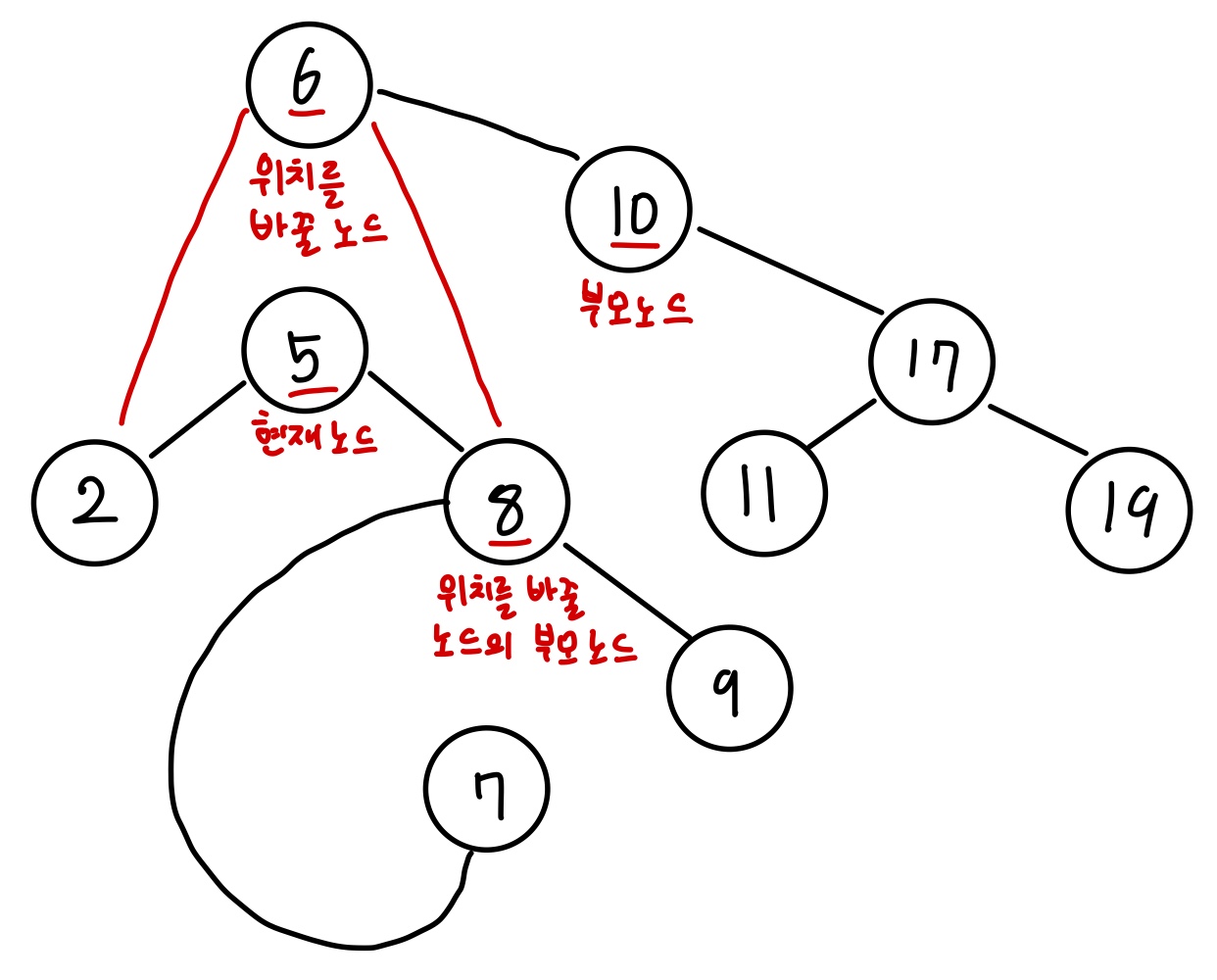
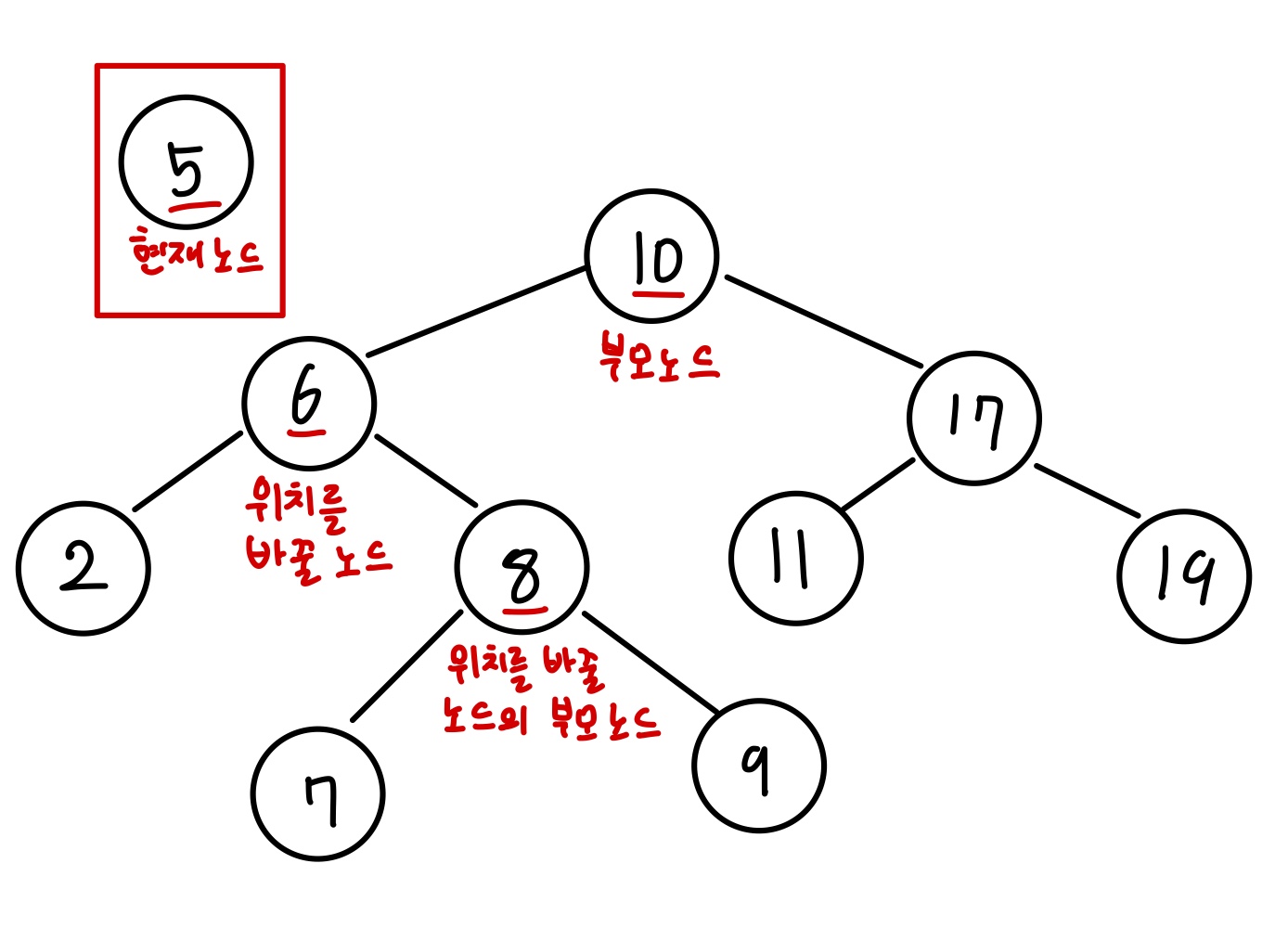
마지막으로 현재 노드를 삭제하면 삭제 동작이 완료됩니다.

하지만 위치를 바꿀 노드(값이 6인 노드)의 오른쪽 포인터가 가리키는 노드가 없다면 위치를 바꿀 노드의 부모 노드(값이 8인 노드)의 왼쪽 포인터가 어떤 노드도 가리키지 않도록 합니다.

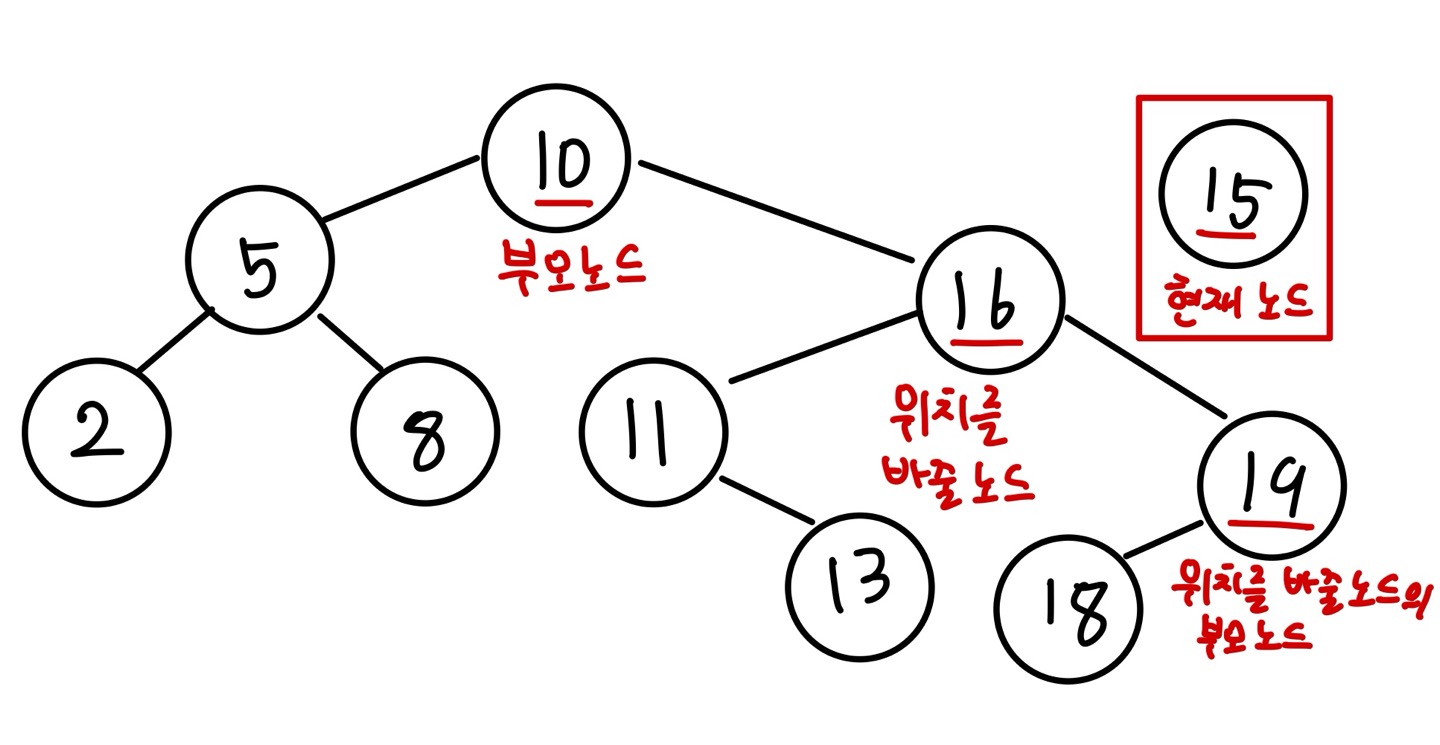
다음은 삭제하려는 노드가 부모 노드의 오른쪽에 있을 경우입니다. 복잡한 동작을 확인하기 위해서 다음 이진 탐색 트리를 예시로 사용하겠습니다.

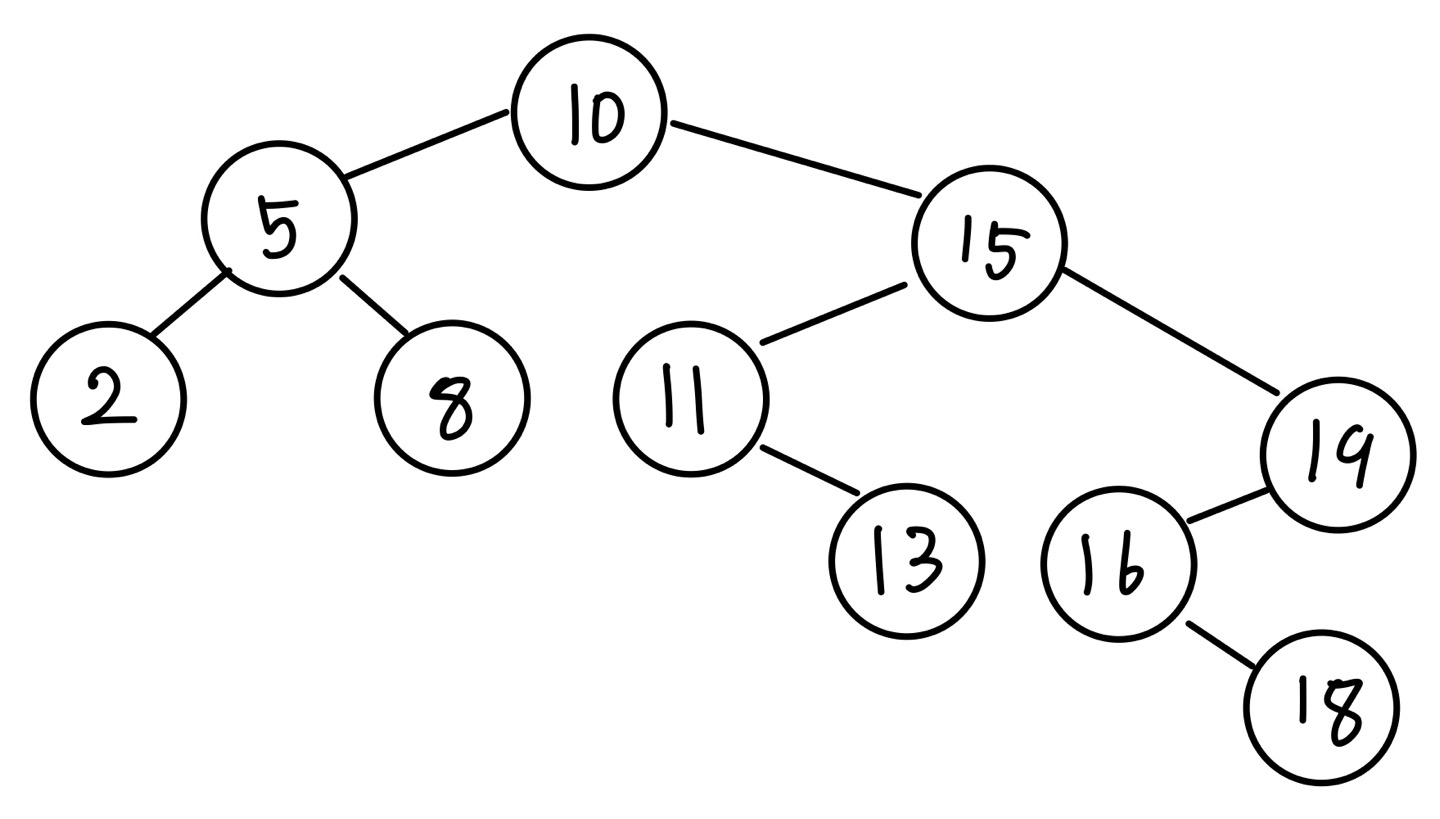
현재 노드가 삭제하려는 노드(값이 15인 노드)인 상태입니다.

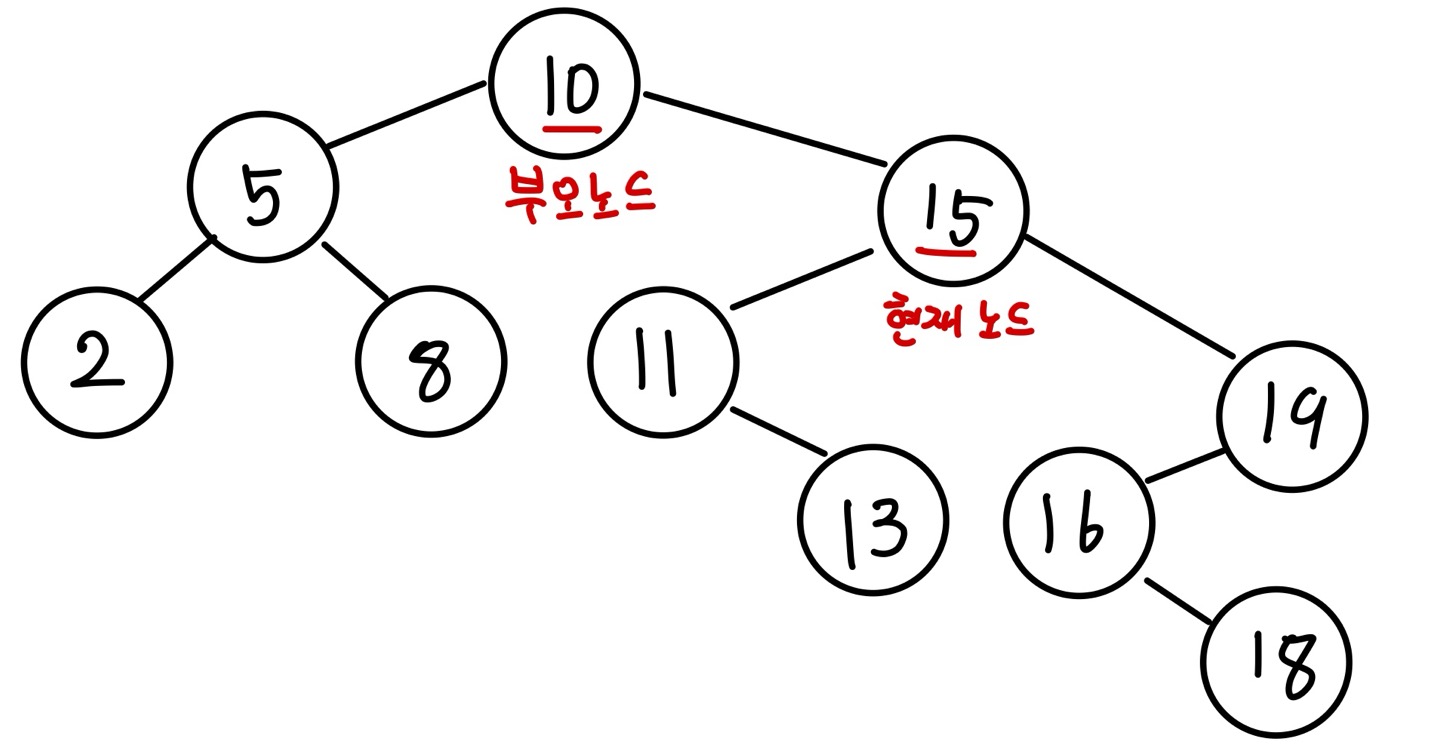
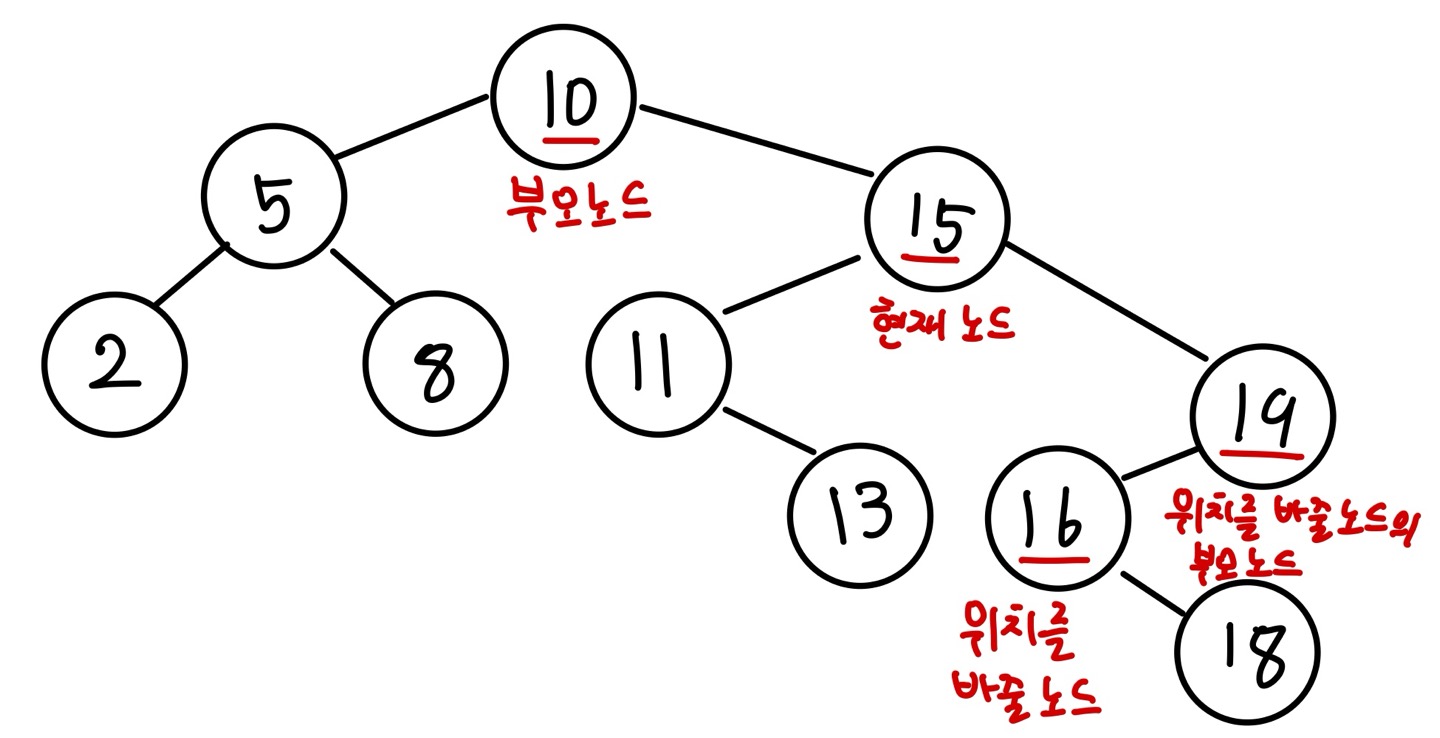
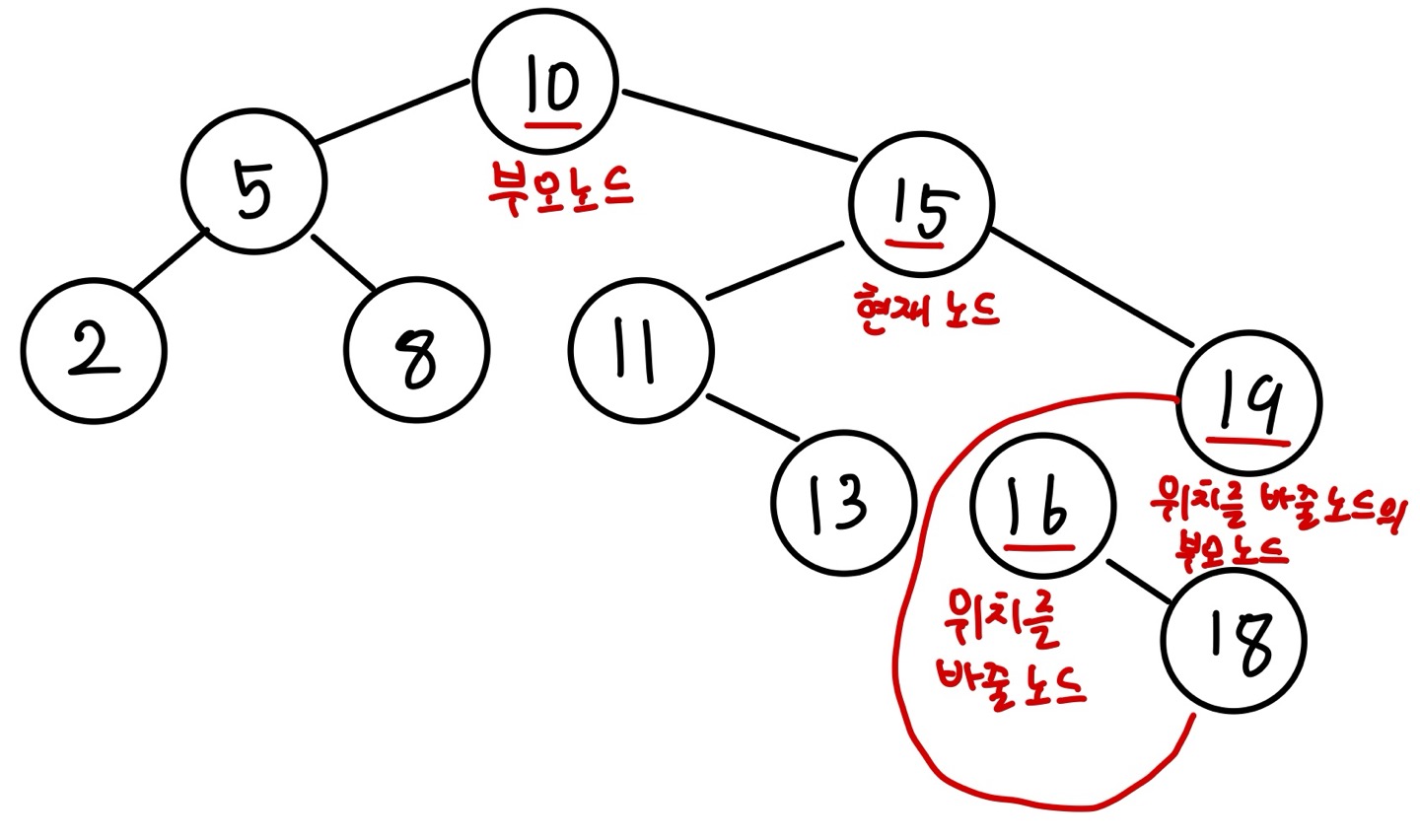
현재 노드를 삭제하려면 부모 노드(값이 10인 노드)의 오른쪽 포인터가 가리킬 노드를 정해야 합니다. 앞의 경우에서처럼 현재 노드의 오른쪽 노드 중 가장 작은 값을 가진 노드를 위치를 변경할 노드로 정하겠습니다. 이번 경우에는 노드의 값이 16인 노드입니다. 이후 과정은 앞선 경우와 동일합니다.


📝 파이썬으로 구현

다음은 파이썬을 사용해서 트리를 구현해보겠습니다.

먼저 이진 탐색 트리의 구성 요소인 노드를 구현해보겠습니다. 노드는 값과 좌우 포인터가 존재 합니다.

class Node:
    def __init__(self, value):
        self.value = value;
        self.left = None;
        self.right = None;

다음은 이진 탐색 트리를 구현해보겠습니다. 해당 이진 탐색 트리는 노드 클래스로 생성된 노드를 루트 노드로 받아 생성됩니다. 

class BST:
    def __init__(self, root): 
        self.root = root

    def insert(self, value):
        # 삽입 동작
        return
        
    def search(self, value):
        # 탐색 동작
        return
        
    def remove(self, value):
        # 삭제 동작
        return

이진 탐색 트리를 구현하기 위해 삽입 동작을 완성해보겠습니다.

def insert(self, value):
        # 현재 노드를 루트 노드로 설정
        current_node = self.root
        
        while True:
            # 현재 노드의 값보다 작을 때
            if current_node.value > value:
                # 왼쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.left != None:
                    current_node = current_node.left
                # 왼쪽 포인터가 가리키는 값이 없다면 삽입
                else:
                    current_node.left = Node(value)
                    break;
            # 현재 노드의 값보다 크거나 같을 때
            else:
                # 오른쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.right != None:
                    current_node = current_node.right
                # 오른쪽 포인터가 가리키는 값이 없다면 삽입
                else:
                    current_node.right = Node(value)
                    break;
        return
        
num_list = [5, 17, 2, 6, 19]

for num in num_list:
    bst.insert(num)

다음은 위 삽입 동작이 정상적으로 실행되었는지 확인하기 위해 탐색 동작을 구현해보겠습니다.

def search(self, value):
        # 현재 노드를 루트 노드로 설정
        current_node = self.root
        
        while True:
            # 현재 노드의 값보다 작을 때
            if current_node.value > value:
                # 왼쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.left != None:
                    current_node = current_node.left
                # 왼쪽 포인터가 가리키는 값이 없다면 종료
                else:
                    break
            # 현재 노드의 값보다 클 때
            elif current_node.value < value:
                # 오른쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.right != None:
                    current_node = current_node.right
                # 오른쪽 포인터가 가리키는 값이 없다면 종료
                else:
                    break
            # 현재 노드의 값과 같을 때
            else:
                print(f"{value}을(를) 찾았습니다.")
                return
            
        print(f"{value}을(를) 찾지 못했습니다.")
        return
        
bst.search(6)  # 6을(를) 찾았습니다.
bst.search(11)  # 11을(를) 찾지 못했습니다.

다음은 삭제 동작입니다. 이진 탐색 트리의 삭제에는 여러 경우를 나누어 생각해야합니다.

def remove(self, value):
        # 현재 노드를 루트 노드로 설정
        current_node = self.root
        # 부모 노드 설정
        parent_node = None
        # 삭제하려는 값의 노드가 존재하는지 확인하는 변수
        isFind = False
        
        # 삭제하려는 노드를 찾음
        while True:
            if current_node.value > value:
                if current_node.left != None:
                    parent_node = current_node
                    current_node = current_node.left
                else:
                    break
            elif current_node.value < value:
                if current_node.right != None:
                    parent_node = current_node
                    current_node = current_node.right
                else:
                    break
            else:
                isFind = True
                break
        
        # 삭제하려는 값의 노드가 없으면 종료
        if not isFind:
            print(f"{value}가(이) 존재하지 않습니다.")
            return
            
        # 1. 삭제하려는 노드가 Leaf Node일 경우
        if current_node.left == None and current_node.right == None:
            if parent_node.left == current_node:
                parent_node.left = None
                print(f"{current_node.value}을(를) 삭제합니다.")
                del current_node
            else:
                parent_node.right = None
                print(f"{current_node.value}을(를) 삭제합니다.")
                del current_node
                
        # 2. 삭제하려는 노드가 두 개의 자식 노드가 있을 경우
        elif current_node.left != None and current_node.right != None:
            change_node = current_node.right
            parent_change_node = current_node
            
            # 삭제하려는 노드가 부모 노드 왼쪽에 있을 경우
            if parent_node.left == current_node:
                # 삭제하려는 노드의 오른쪽에서 가장 작은 값을 가진 노드를 찾는 과정
                while True:
                    if change_node.left != None:
                        parent_change_node = change_node
                        change_node = change_node.left
                    else:
                        break
                
                # 위치를 바꿀 노드의 오른쪽에 자식 노드가 있을 경우
                if change_node.right != None:
                    parent_change_node.left = change_node.right
                    parent_node.left = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                    
                # 위치를 바꿀 노드의 오른쪽에 자식 노드가 없을 경우   
                else:
                    parent_change_node.left = None
                    parent_node.left = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
            # 삭제하려는 노드가 부모 노드 오른쪽에 있을 경우
            else:
                # 삭제하려는 노드의 오른쪽에서 가장 작은 값을 가진 노드를 찾는 과정
                while True:
                    if change_node.left != None:
                        parent_change_node = change_node
                        change_node = change_node.left
                    else:
                        break
               # 위치를 바꿀 노드의 오른쪽에 자식 노드가 있을 경우
                if change_node.right != None:
                    parent_change_node.left = change_node.right
                    parent_node.right = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                    
                # 위치를 바꿀 노드의 오른쪽에 자식 노드가 없을 경우   
                else:
                    parent_change_node.left = None
                    parent_node.right = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node 
        # 3. 삭제하려는 노드가 한 개의 자식 노드가 있을 경우
        else:
            # 자식 노드가 왼쪽에 있을 경우
            if current_node.left != None:
                # 삭제하려는 노드가 부모 노드의 왼쪽에 있을 경우
                if parent_node.left == current_node:
                    parent_node.left = current_node.left
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                # 삭제하려는 노드가 부모 노드의 오른쪽에 있을 경우
                else:
                    parent_node.right = current_node.left
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
            # 자식 노드가 오른쪽에 있을 경우
            else:
                # 삭제하려는 노드가 부모 노드의 왼쪽에 있을 경우
                if parent_node.left == current_node:
                    parent_node.left = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                # 삭제하려는 노드가 부모 노드의 오른쪽에 있을 경우
                else:
                    parent_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
        return

num_list = [5, 15, 2, 8, 6, 7, 9, 11, 13, 16, 18, 19]

for num in num_list:
    bst.insert(num)

bst.search(6)  # 6을(를) 찾았습니다.
bst.search(15)  # 15을(를) 찾았습니다.

bst.remove(6)  # 6을(를) 삭제합니다.
bst.remove(15)  # 15을(를) 삭제합니다.

bst.search(6)  # 6을(를) 찾지 못했습니다.
bst.search(15)  # 15을(를) 찾지 못했습니다.

다음은 모든 동작을 구현한 이진 탐색 트리의 전체 코드입니다.

class Node:
    def __init__(self, value):
        self.value = value;
        self.left = None;
        self.right = None;
        
class BST:
    def __init__(self, root): 
        self.root = root

    def insert(self, value):
        # 현재 노드를 루트 노드로 설정
        current_node = self.root
        
        while True:
            # 현재 노드의 값보다 작을 때
            if current_node.value > value:
                # 왼쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.left != None:
                    current_node = current_node.left
                # 왼쪽 포인터가 가리키는 값이 없다면 삽입
                else:
                    current_node.left = Node(value)
                    break;
            # 현재 노드의 값보다 크거나 같을 때
            else:
                # 오른쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.right != None:
                    current_node = current_node.right
                # 오른쪽 포인터가 가리키는 값이 없다면 삽입
                else:
                    current_node.right = Node(value)
                    break;
        return
        
    def search(self, value):
        # 현재 노드를 루트 노드로 설정
        current_node = self.root
        
        while True:
            # 현재 노드의 값보다 작을 때
            if current_node.value > value:
                # 왼쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.left != None:
                    current_node = current_node.left
                # 왼쪽 포인터가 가리키는 값이 없다면 종료
                else:
                    break
            # 현재 노드의 값보다 클 때
            elif current_node.value < value:
                # 오른쪽 포인터가 가리키는 값이 있다면 이동
                if current_node.right != None:
                    current_node = current_node.right
                # 오른쪽 포인터가 가리키는 값이 없다면 종료
                else:
                    break
            # 현재 노드의 값과 같을 때
            else:
                print(f"{value}을(를) 찾았습니다.")
                return
            
        print(f"{value}을(를) 찾지 못했습니다.")
        return
        
    def remove(self, value):
        # 현재 노드를 루트 노드로 설정
        current_node = self.root
        # 부모 노드 설정
        parent_node = None
        # 삭제하려는 값의 노드가 존재하는지 확인하는 변수
        isFind = False
        
        # 삭제하려는 노드를 찾음
        while True:
            if current_node.value > value:
                if current_node.left != None:
                    parent_node = current_node
                    current_node = current_node.left
                else:
                    break
            elif current_node.value < value:
                if current_node.right != None:
                    parent_node = current_node
                    current_node = current_node.right
                else:
                    break
            else:
                isFind = True
                break
        
        # 삭제하려는 값의 노드가 없으면 종료
        if not isFind:
            print(f"{value}가(이) 존재하지 않습니다.")
            return
            
        # 1. 삭제하려는 노드가 Leaf Node일 경우
        if current_node.left == None and current_node.right == None:
            if parent_node.left == current_node:
                parent_node.left = None
                print(f"{current_node.value}을(를) 삭제합니다.")
                del current_node
            else:
                parent_node.right = None
                print(f"{current_node.value}을(를) 삭제합니다.")
                del current_node
                
        # 2. 삭제하려는 노드가 두 개의 자식 노드가 있을 경우
        elif current_node.left != None and current_node.right != None:
            change_node = current_node.right
            parent_change_node = current_node
            
            # 삭제하려는 노드가 부모 노드 왼쪽에 있을 경우
            if parent_node.left == current_node:
                # 삭제하려는 노드의 오른쪽에서 가장 작은 값을 가진 노드를 찾는 과정
                while True:
                    if change_node.left != None:
                        parent_change_node = change_node
                        change_node = change_node.left
                    else:
                        break
                
                # 위치를 바꿀 노드의 오른쪽에 자식 노드가 있을 경우
                if change_node.right != None:
                    parent_change_node.left = change_node.right
                    parent_node.left = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                    
                # 위치를 바꿀 노드의 오른쪽에 자식 노드가 없을 경우   
                else:
                    parent_change_node.left = None
                    parent_node.left = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
            # 삭제하려는 노드가 부모 노드 오른쪽에 있을 경우
            else:
                # 삭제하려는 노드의 오른쪽에서 가장 작은 값을 가진 노드를 찾는 과정
                while True:
                    if change_node.left != None:
                        parent_change_node = change_node
                        change_node = change_node.left
                    else:
                        break
               # 위치를 바꿀 노드의 오른쪽에 자식 노드가 있을 경우
                if change_node.right != None:
                    parent_change_node.left = change_node.right
                    parent_node.right = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                    
                # 위치를 바꿀 노드의 오른쪽에 자식 노드가 없을 경우   
                else:
                    parent_change_node.left = None
                    parent_node.right = change_node
                    change_node.left = current_node.left
                    change_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node 
        # 3. 삭제하려는 노드가 한 개의 자식 노드가 있을 경우
        else:
            # 자식 노드가 왼쪽에 있을 경우
            if current_node.left != None:
                # 삭제하려는 노드가 부모 노드의 왼쪽에 있을 경우
                if parent_node.left == current_node:
                    parent_node.left = current_node.left
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                # 삭제하려는 노드가 부모 노드의 오른쪽에 있을 경우
                else:
                    parent_node.right = current_node.left
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
            # 자식 노드가 오른쪽에 있을 경우
            else:
                # 삭제하려는 노드가 부모 노드의 왼쪽에 있을 경우
                if parent_node.left == current_node:
                    parent_node.left = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
                # 삭제하려는 노드가 부모 노드의 오른쪽에 있을 경우
                else:
                    parent_node.right = current_node.right
                    print(f"{current_node.value}을(를) 삭제합니다.")
                    del current_node
        return
        
node = Node(10)
bst = BST(node)

num_list = [5, 15, 2, 8, 6, 7, 9, 11, 13, 16, 18, 19]

for num in num_list:
    bst.insert(num)

bst.search(6)  # 6을(를) 찾았습니다.
bst.search(15)  # 15을(를) 찾았습니다.

bst.remove(6)  # 6을(를) 삭제합니다.
bst.remove(15)  # 15을(를) 삭제합니다.

bst.search(6)  # 6을(를) 찾지 못했습니다.
bst.search(15)  # 15을(를) 찾지 못했습니다.

🎁 관련 문제

profile
LazyMG
개발 기록
이전 포스트

[자료구조] 파이썬으로 해시 테이블 구현하기(feat. 딕셔너리)

다음 포스트

[자료구조] 파이썬으로 힙 구현하기

0개의 댓글