백준 #11723. 집합 문제를 풀고 정리하는 비트마스킹 테크닉, 기법(?!?!)

배경

데이터들은 0과 1의 집합이라고 하죠. 비트는 네트워크 외에도 운영체제 등에서 자주 접할 수 있습니다. 최적의 성능을 위해 여러 곳에서 쓰이고 있는게 비트인데요, 이 비트를 알고리즘 문제 풀이 내 여러 개의 상태를 표시할 때도 유용하게 쓸 수 있습니다!

비트마스킹

비트

위에서 말한 비트란 이진 숫자입니다. 0, 1 값을 가질 수 있고 true/flase, on/off 상태를 나타냅니다.

비트마스킹

비트의 위와 같은 특성을 이용해 정수의 이진수 표현을 자료구조로 쓰는 테크닉, 기법입니다.

비트마스킹을 사용해 더욱 효율적으로 동작하는 것을 확인해보겠습니다.

• 길이가 4인 집합 {0, 1, 2, 3}의 몇가지 부분집합을 표현
  • Array사용
    boolean[] array1 = {1, 0, 0, 0};
    boolean[] array2 = {1, 1, 0, 0};
    boolean[] array2 = {0, 0, 1, 1};
  • 비트마스크 사용
    {0} -> 1000
    {0, 1} -> 1100
    {2, 3} -> 0011
    비트마스크 사용 시 메모리사용이 줄어든 것을 확인할 수 있음

비트연산

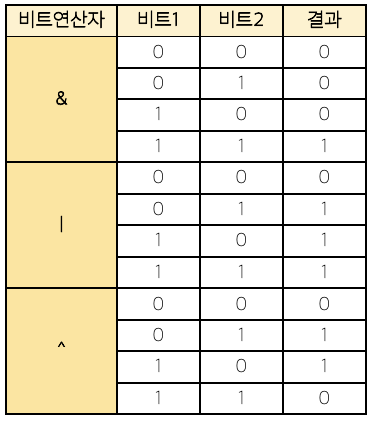
AND 연산, &
대응하는 두 비트가 모두 1일 때 1 반환
OR 연산, |
대응하는 두 비트 중 하나라도 1이라면 1, 아니면 0 반환
XOR 연산, ^
대응하는 두 비트가 다르면 1, 같으면 0을 반환
NOT 연산, ~
비트의 값을 반전
Shift 연산, <<, >>
왼쪽 또는 오른쪽으로 비트를 이동

활용

#1. 1010 부분집합에 2번째 요소를 삽입해 1110으로 만들고 싶다!

// bit = 1010
bit = bit | (1 << 2)

시프트 연산을 통해 2번째 비트만 1로 할당되어 있는 이진수로 만들고, or 연산을 통해 원하는 결과를 얻음
#2. 2번째 비트값을 0으로!

// bit = 1110
bit = bit | ~(1 << 2)

#3. i번째 비트의 값을 조회

if (bit & (1 << i) != 0) i번째 비트는 1
else i번째 비트는 0

#4. toggle (i번째 비트를 0->1, 1->0 반전)

bit = bit ^ (1 << i)

xor연산을 하면 다른 비트들은 1^0=1, 0^0=0이어서 영향을 받지 않고, 해당 비트는 1^1=0, 0^1=1이기 때문에 전환할 수 있음

🙇🏻‍♀️📚