Regularization

📕 Regularization

• Weight가 너무 큰 값들을 가지지 않도록 하는 것이다.

📗 Why?

• Weight가 너무 큰 값을 가지게 되면 과하게 구불구불한 형태의 함수가 만들어지는데, Regularization은 이런 모델의 복잡도를 낮추기 위한 방법이다.
• Regularization은 단순하게 cost function을 작아지는 쪽으로 학습하면 특정 가중치 값들이 커지면서 결과를 나쁘게 만들기 때문에 cost function을 바꾼다.

📘 How?

✍ L1 Regularization

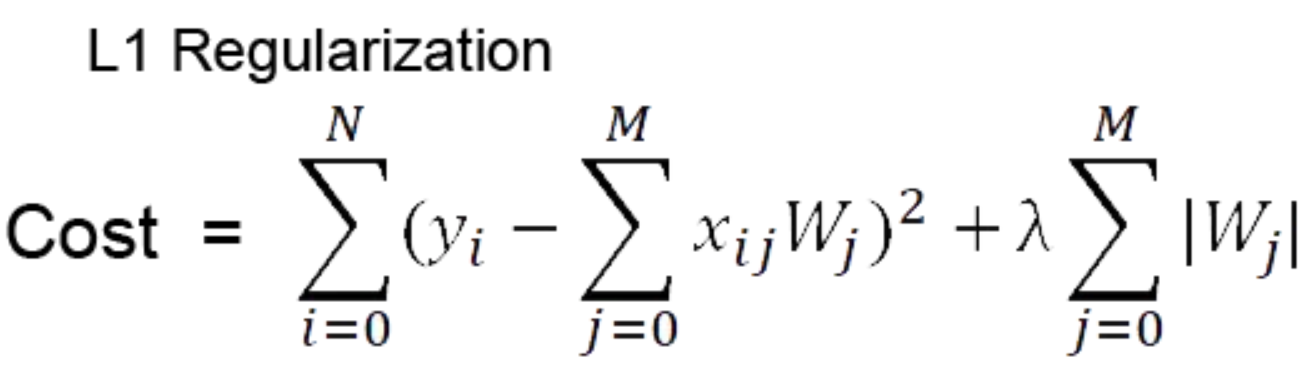
Regularization에서는 학습의 방향이 단순하게 Cost값이 작아지는 방향으로만 진행되는게 아니라, Weight값들 역시 최소가 되는 방향으로 진행을 하게 된다.

✍ L2 Regularization

L1과 다른 점은 Weight값이 절대값이 아닌 제곱 값이라는 점이다.

📙 Regularization Code (Pytorch)

def compute_cost_with_regularization(A3, Y, parameters, lambd):
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]
    
    cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
    
    L2_regularization_cost = 1/m * lambd/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
    
    cost = cross_entropy_cost + L2_regularization_cost
    
    return cost
    
def backward_propagation_with_regularization(X, Y, cache, lambd):
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
    
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
    
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
    db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}
    return gradients

---

Reference

https://simsim231.tistory.com/93
https://medium.com/analytics-vidhya/l1-vs-l2-regularization-which-is-better-d01068e6658c
https://velog.io/@yelim421/RegularizationL2-Regularization-Dropout#l2-regularization