
이번 글에서는 정규화(Regularization)에 대해 알아보겠다.
만약 우리가 가지고 있는 데이터가 그렇게 크지 않다면, overfitting이 될 가능성이 크기 때문에 overfitting되지 않게 하기 위해 Regularization을 꼭 해줘야 한다.
출처
왜 정규화가 필요한지, 또 정규화를 하게 되면 어떻게 되는지 알아보자.
Packages
# import packages
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import scipy.io
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
from testCases import *
from public_tests import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2위에서 다운받은 데이터셋은
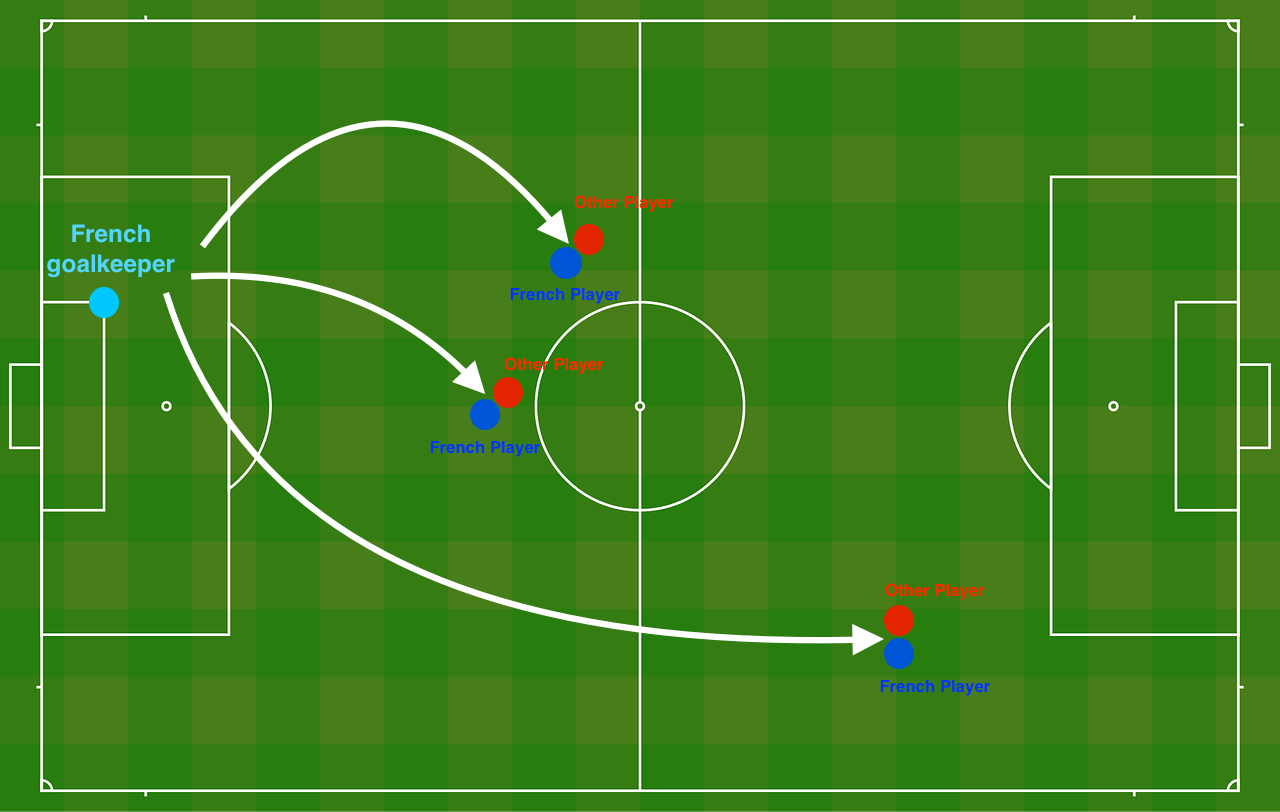
이 그림을 보면서 이해하면 편하다. 프랑스 골키퍼가 어느 곳으로 공을 차야 다른 프랑스 플레이어들이 헤딩하기 좋을지에 대한 데이터이다.
데이터를 로드해보자.
train_X, train_Y, test_X, test_Y = load_2D_dataset()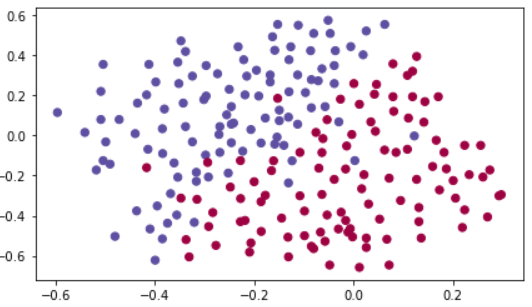
보라색 점은 프랑스 플레이어들이 헤딩을 잘 할 수 있는 곳이다.
빨간색 점은 상대방 플레이어들이 헤딩을 잘 할 수 있는 곳이다.
딥러닝 모델을 이용해서 골키퍼가 어떤 곳으로 공을 패스해야 할지 알아보자.
정규화를 한 것과 하지 않은 것을 비교해보기 위해서 먼저 정규화 하지 않은 모델을 만들어보자.
Non-Regularized Model
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert (lambd == 0 or keep_prob == 1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters이제 이 모델을 훈련시켜보자.
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)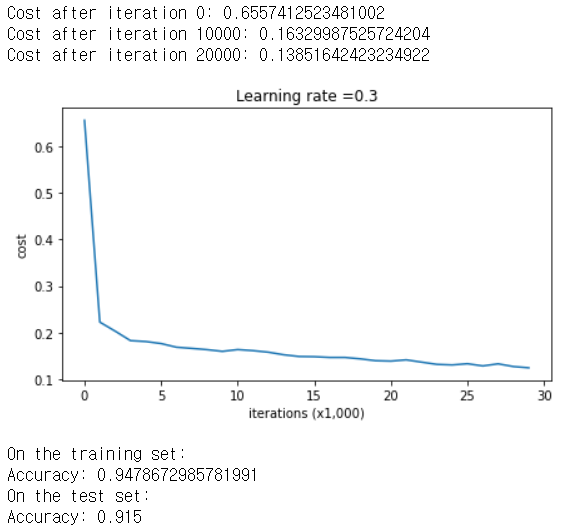
트레이닝 세트에서의 정확도는 94%, 테스트 세트에서의 정확도는 91%이다. 다시한번 그림으로 확인해보자.
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)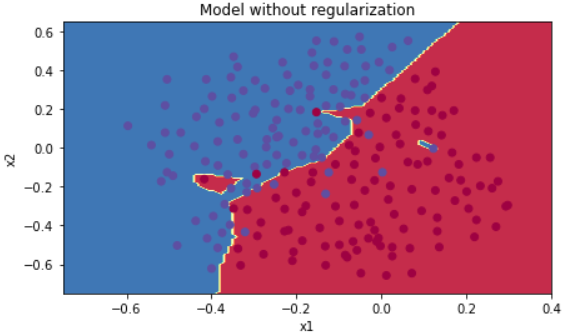
역시 엄청 이상하다. 저 자잘자잘한 부분까지 다 계산이 됐다. 이런 그래프를 맨 처음 부분에서 언급했던 Overfitting이라고 한다. 이런 부분들을 줄이기 위해서 두가지 기술을 도입할 수 있다.
- L2 Regularization
- Dropout
아래에서 알아보자.
L2 Regularization
가장 보편적인 overfitting을 줄이는 방법은 L2 Regularization이다. 이 방법은 cost function을
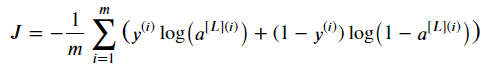
위 식에서
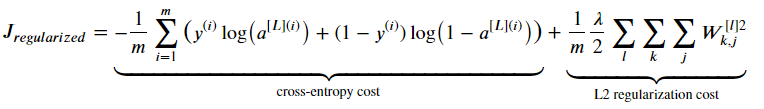
아래 식으로 정규화 해 준다. 아래 코드에서 cost function을 어떻게 계산하는지 살펴보자.
Compute cost with regularization
def compute_cost_with_regularization(A3, Y, parameters, lambd):
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
L2_regularization_cost = 1/m * lambd/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
cost = cross_entropy_cost + L2_regularization_cost
return costA3, t_Y, parameters = compute_cost_with_regularization_test_case()
cost = compute_cost_with_regularization(A3, t_Y, parameters, lambd=0.1)
print("cost = " + str(cost))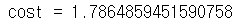
여기서 cost function을 바꿨으니, 당연히 backward propagation도 바꿔줘야 한다!
Backward propagation with regularization
def backward_propagation_with_regularization(X, Y, cache, lambd):
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientsgradients를 확인해보자.
t_X, t_Y, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(t_X, t_Y, cache, lambd = 0.7)
print ("dW1 = \n"+ str(grads["dW1"]))
print ("dW2 = \n"+ str(grads["dW2"]))
print ("dW3 = \n"+ str(grads["dW3"]))
이제 모델에서 실행시켜보자.
모델 함수는 compute_cost대신 compute_cost_with_regularization을, bacoward_propagation대신 backward_propagation_with_regularization을 부른다.
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)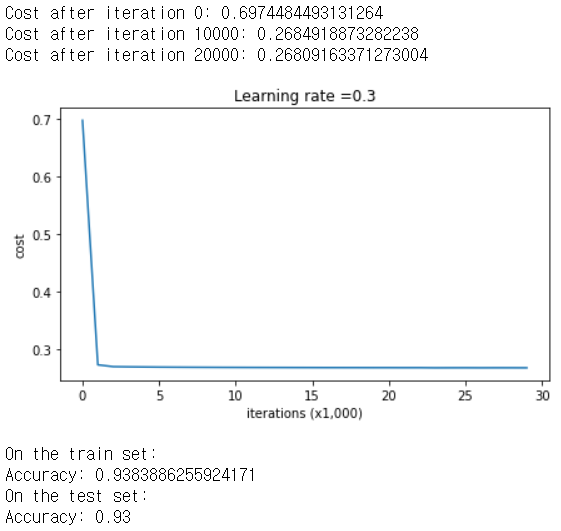
트레인과 테스트 세트에서 모드 93% 비슷한 수치의 정확도가 나왔다.
그림으로 다시 확인해보자.
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)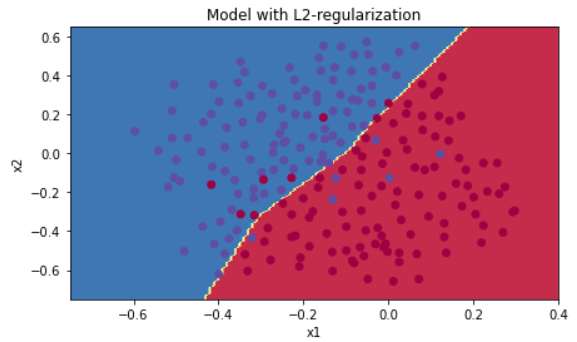
확인할 수 있는 점:
- 람다값은 hyperparameter로써 dev set을 튜닝할 때 쓰일 수 있다.
- L2 Regularization은 경계선을 부드럽게 해준다. 만약 람다가 너무 크면 oversmooth가 될 수 있어 bias값이 크게 나오므로 주의하자.
Dropout
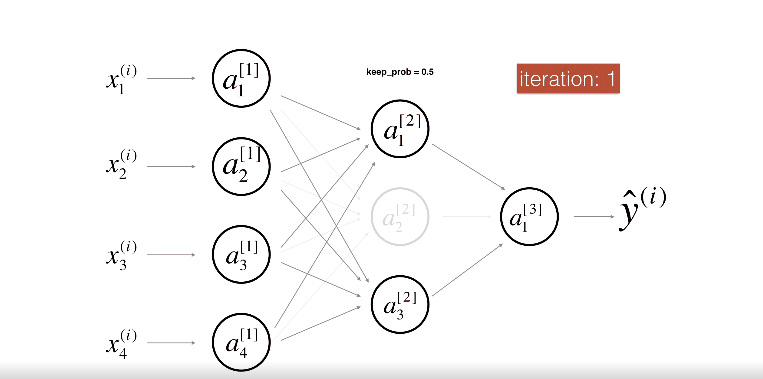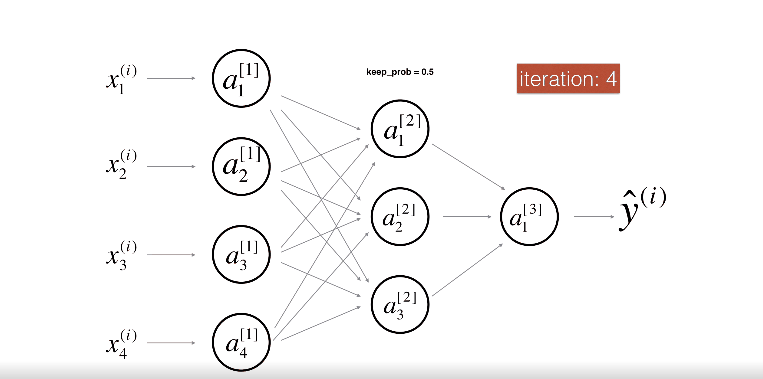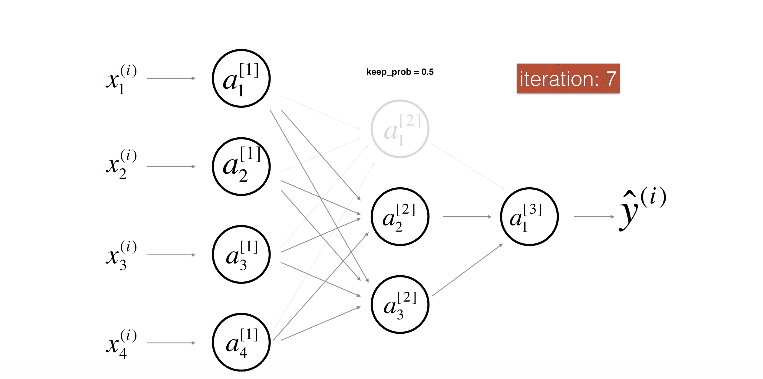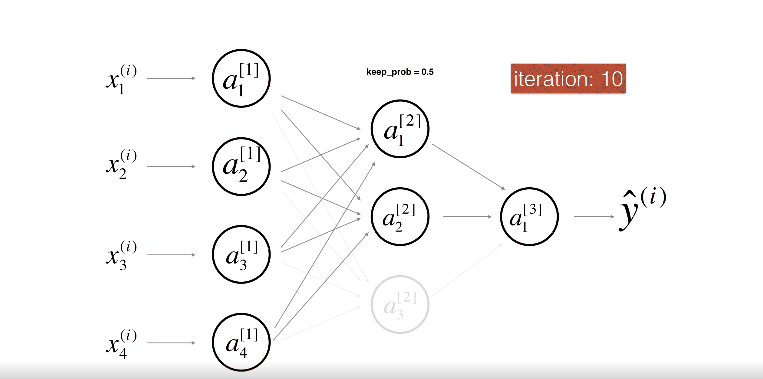
위 그림은 두번째 레이어를 Drop-out하는 모습이다.
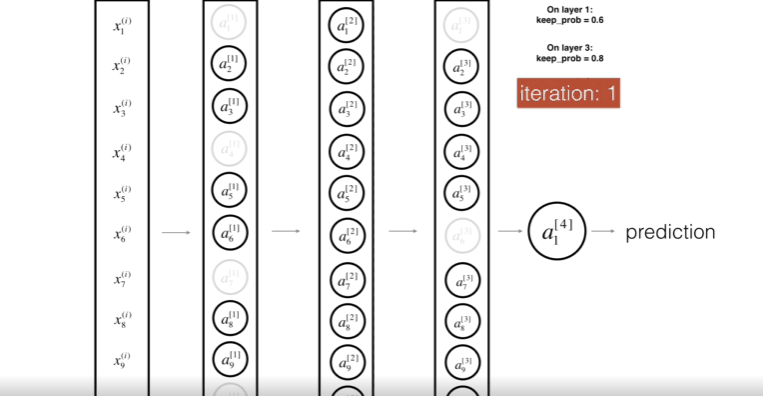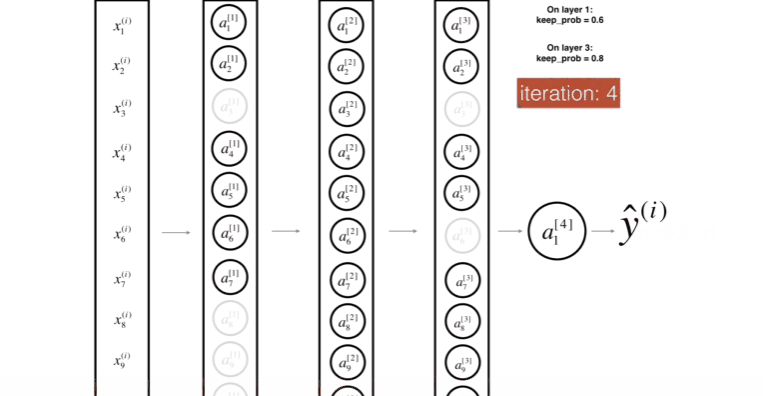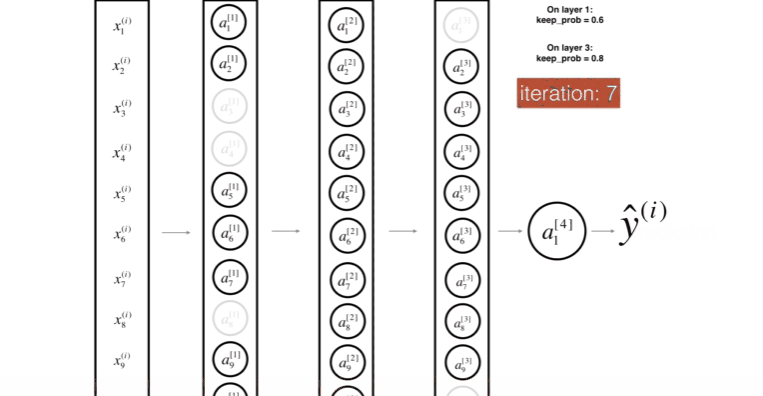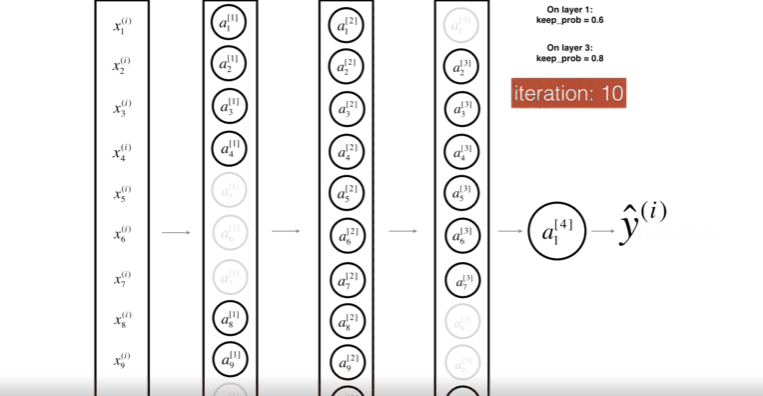
위 그림은 첫번째 레이어를 40%의 확률로 셧다운 하고, 세번째 레이어를 20%의 확률로 셧다운 하는 모습이다.
forward propagation부터 작성해보자.
Forward Propagation with Dropout
여기서는 세 개의 레이어 중에서 첫번째와 두번째 레이어를 드롭아웃시킬 것이다.
-
먼저 D[1]을 A[1]과 같은 사이즈의 랜덤 매트릭스로 만들어 준다.
D1 = np.random.rand(A1.shape[0],A1.shape[1])이 코드로 구현하면 된다. -
두 번째로 D[1]의 입구를
keep_prob의 확률로 1로 만들어준다. 만약keep_prob가 70%라면 70%의 확률로 1이 될 것이고, 30%의 확률로 0(drop-out)이 될 것이다. 이를 이와 같이 구현해준다.D1 = (D1 < keep_prob).astype(int) -
세번째로 D[1]이 다른 매트릭스와 곱해질 때 몇개의 값들을 shut down시킬 것이다. 즉, A[1]=A[1]*D[1]로 만들어준다.
A1=A1xD1역시 간단하게 구현할 수 있다. -
마지막으로 A[1]을
keep_prob으로 나눠준다. 이를 통해서 cost 의 결과가 drop-out와 같은 결과를 낼 수 있다. 이 단계는 inverted dropout으로 불린다.
이제 forward_propagation_with_dropout함수를 구현해보자.
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0],A1.shape[1])
D1 = (D1 < keep_prob).astype(int)
A1 = A1 * D1
A1 = A1 / keep_prob
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0],A2.shape[1])
D2 = (D2 < keep_prob).astype(int)
A2 = A2 * D2
A2 = A2 / keep_prob
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cachet_X, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(t_X, parameters, keep_prob=0.7)
print ("A3 = " + str(A3))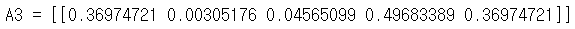
마지막으로 backward propagation with dropout을 알아보자.
Backward Propagation with Dropout
-
forward에서 A[1]=A[1]*D[1]로 만들어 줌으로써 다른 매트릭스와 곱해질 때 몇개의 값들을 shut down시켰다. 여기서는 같은 뉴런들을 셧다운 시키기 위해서 D[1]과 dA1을 곱해줄 것이다.
-
마지막 단계와 같이 backward에서는
dA1을keep_prob로 다시 나눠준다.
구현해보자.
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2
dA2 = dA2 / keep_prob
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1
dA1 = dA1 / keep_prob
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientst_X, t_Y, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(t_X, t_Y, cache, keep_prob=0.8)
print ("dA1 = \n" + str(gradients["dA1"]))
print ("dA2 = \n" + str(gradients["dA2"]))
keep_prob의 값을 0.86으로 하고 모델에서 학습시켜보자.
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)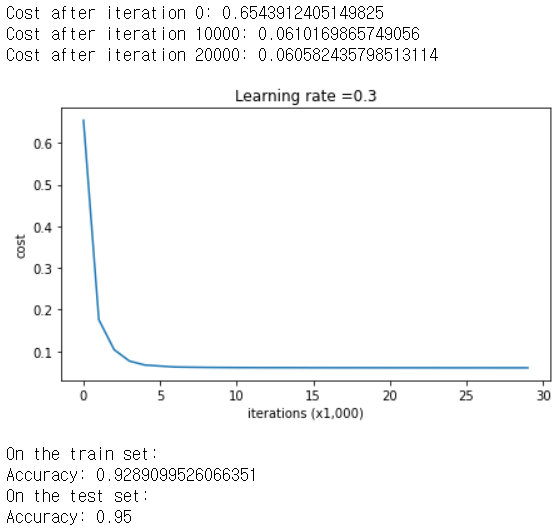
테스트의 정확도가 다시 95%로 올라갔다는 것을 확인할 수 있다.
그림으로 확인해보자.
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)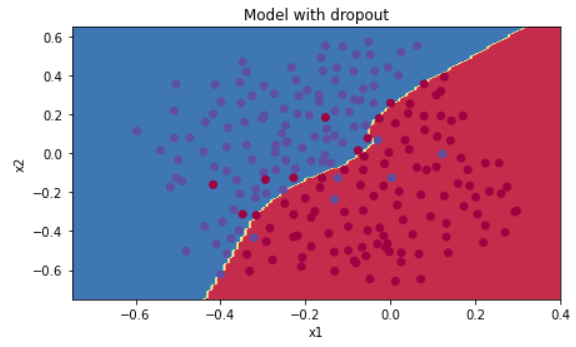
Dropout은 반드시 training 세트에서만 사용해야 한다. 테스트에서 사용하지 않게 주의하자.
Conclusions
세 모델을 비교한 표이다.

Regularization은 트레이닝 세트에서의 정확도를 저하시킨다. 왜냐하면 네트워크가 트레이닝 세트에 딱 맞는 기능들을 제한(dropout)하기 때문인데, 궁극적으로 테스트에서 더 나은 정확도를 제공하기 때문에 시스템에는 도움이 된다고 말할 수 있다.
여기서 정규화에 대한 설명을 마치겠다.
