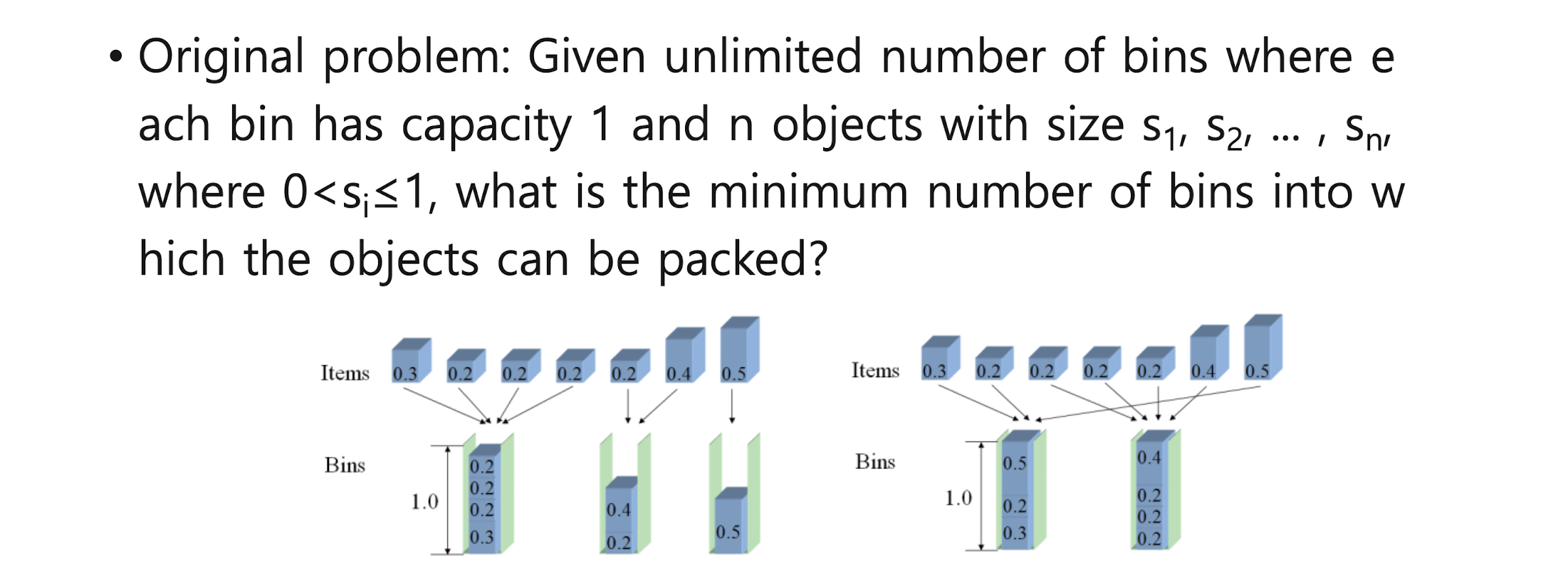
Course Introduction & Introduction to Computer Algorithms
알고리즘에 대해 고려해야할 것들
- Finiteness : Must terminate after a finite number of steps
- Effectiveness : : Must be developed by basic and feasible operations
so we can trace by using computer or paper/pencil- Scalability : Work out for “large” inputs
< Algorithm Example >
Search algorithm
- linear search O(n)
- binary search O(log n)
Fibonacci Numbers
- recursive algorithm O(2^n)
- iterative algorithm O(n)
Greatest Common Diviser 최대공약수
- trivial algorithm
- factorization
- euclid algorithm O(n)
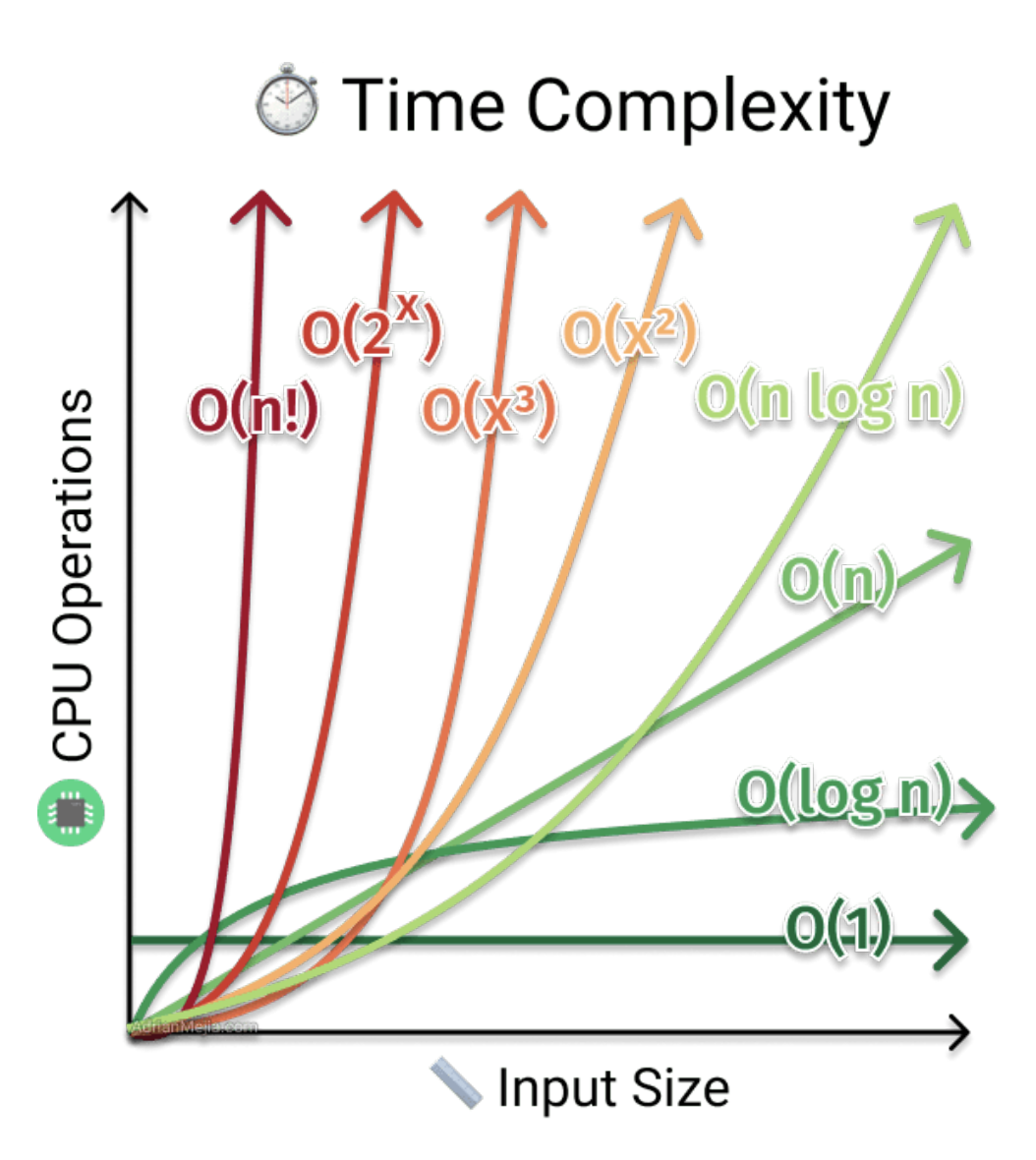
1. Algorithm Analysis
Time complexity
- Worst-case time complexity : mostly used. too pessimistic
W(n) = max{t(I)|I ∈ Dn}, where is the set of possible input size n- Average-case time complexity: rarely used
A(n) = ∑I∈Dn P(I)t(I), where p(I) is the probability that the input n occur among Dn- Amortized time complexity : Amortized analysis는 더 비싼 작업의 비용을 여러 작업에 분산시킴으로써 각 작업의 평균 실행 시간을 보장합니다.
Ex) stack operations
Two methods of an amortization : accounting method, potential method
• Accounting method : Pay extra money for some operations as a credit.
Use that credit to pay higher cost of some later operations.
• Potential method: potential method란 데이터 구조의 상태를 실수로 매핑하는 potential function을 할당하는 기술입니다. potential function은 현재 상태에서 "원하는" 상태로 데이터 구조를 가져 오기 위해 수행해야 할 추가 작업량을 나타냅니다. 연산의 amortized cost는 연산의 실제 비용에 연산으로 인한 potential 변경 값을 더한 값으로 정의됩니다.
예를 들어, 각 push 연산이 2달러 비용이 들고 각 pop 연산이 1달러 비용이 드는 스택 데이터 구조가 있다고 가정해봅시다. 우리는 potential function을 스택에 있는 원소의 수로 정의합니다. 빈 스택의 초기 potential은 0입니다. push 연산을 수행하면, 실제 비용은 2달러이고 potential은 스택에 하나의 원소가 추가되었기 때문에 1만큼 증가합니다. 따라서 push 연산의 amortized cost는 2 + 1 = 3달러입니다. pop 연산을 수행하면, 실제 비용은 1달러이고 potential은 스택에서 하나의 원소가 제거되었기 때문에 1만큼 감소합니다. 따라서 pop 연산의 amortized cost는 1 - 1 = 0달러입니다.
=> the amortized cost of any operation is O(1)
Space complexity
: 알고리즘이 실행되는 동안 필요한 메모리 양Optimality
: the minimum amount of work to solve it.
the lower bound of a given problem.
best possible
- How to prove that an algorithm is optimal?
=> the upper bound W(n) = the lower bound L(n)
Order notations
- Big-O Notation O() : 최악의 경우 시간 복잡도
- Omega Notation Ω() : 최선의 경우 시간 복잡도
- Theta Notation θ () : 최선 및 최악의 경우 시간 복잡도를 모두 고려 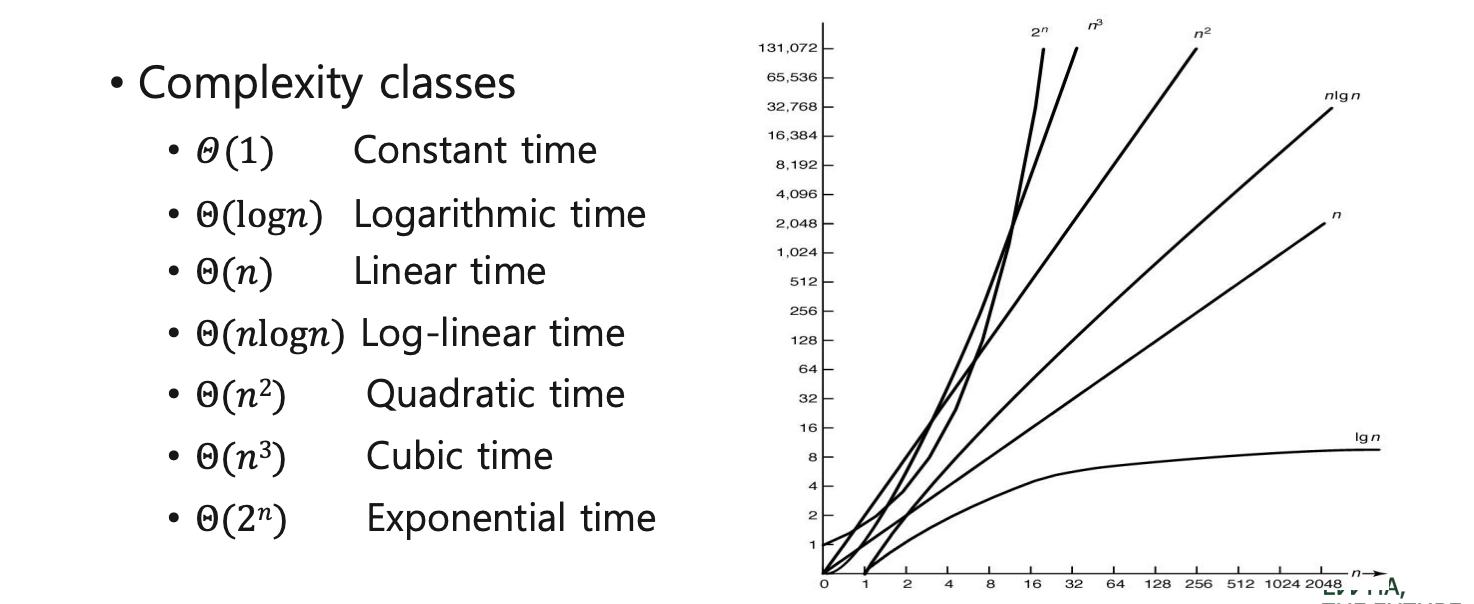
- How to compare the efficiency of algorithms?
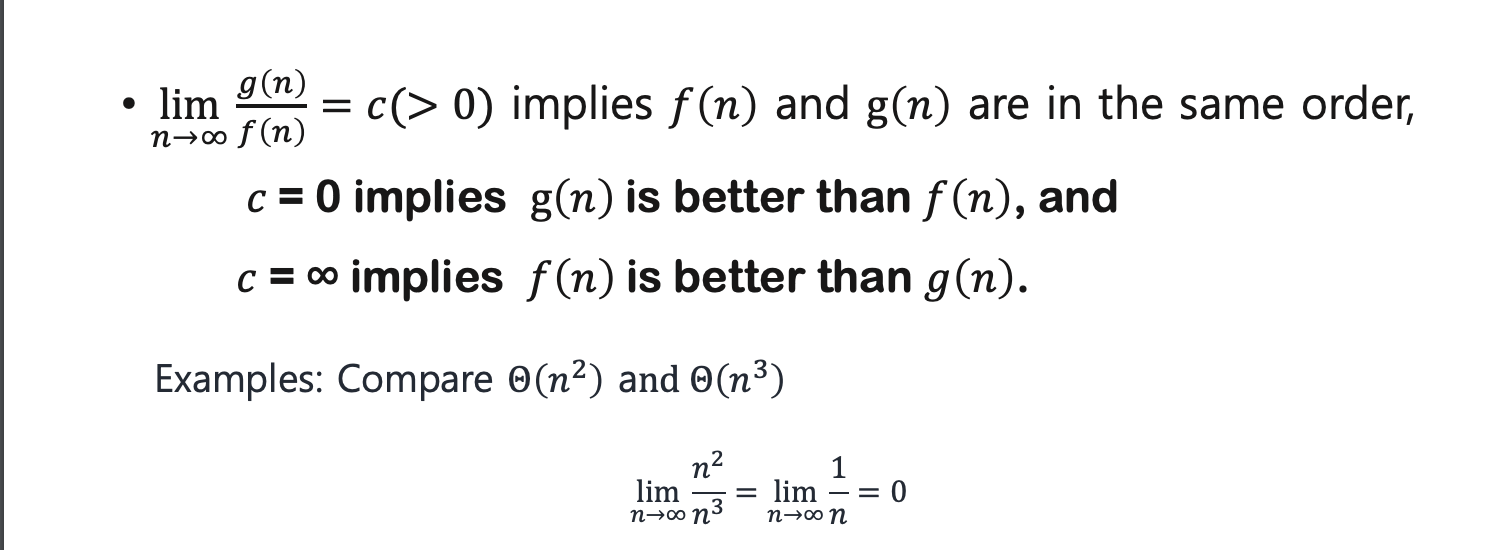
• L'Hospital's Rule
2. Divide and Conquer

Binary search
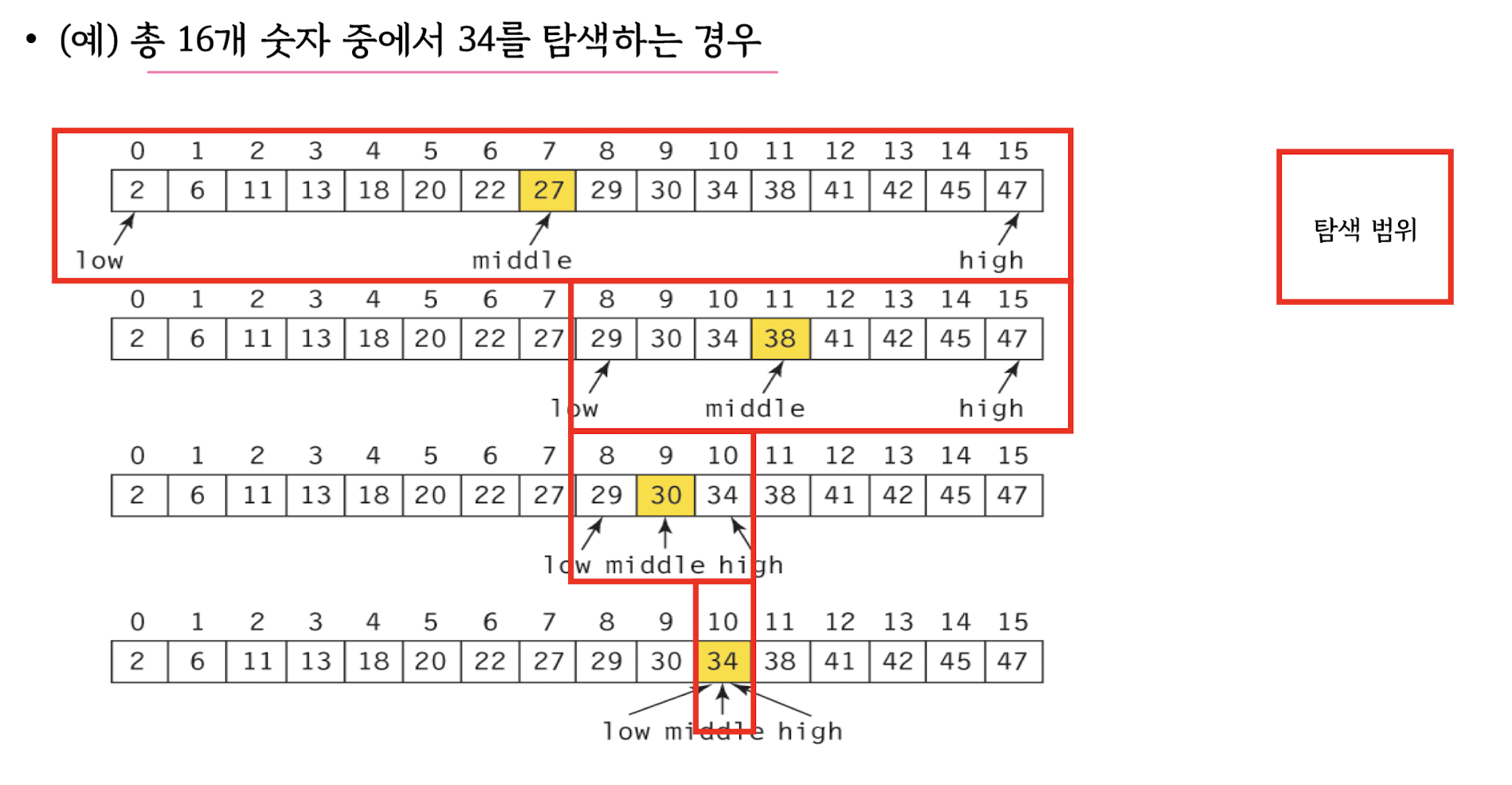

Find the maximum

Multiplication
- **Recursive definition**
- Multiplication with divide and conquer
 이 코드는 먼저 x와 y가 0이면 0을 반환하는 기본 케이스를 처리합니다. 그렇지 않으면 y를 2로 나누고, 몫을 구한 후, 다시 자기 자신을 호출합니다. 이때 x와 y/2를 인수로 전달합니다. 이 과정을 재귀적으로 반복하며, y가 0이 될 때까지 함수를 호출합니다.
이 코드는 먼저 x와 y가 0이면 0을 반환하는 기본 케이스를 처리합니다. 그렇지 않으면 y를 2로 나누고, 몫을 구한 후, 다시 자기 자신을 호출합니다. 이때 x와 y/2를 인수로 전달합니다. 이 과정을 재귀적으로 반복하며, y가 0이 될 때까지 함수를 호출합니다.
만약 y가 짝수(즉, 2로 나누어 떨어지는 수)라면, 이전에 계산된 z를 2배하여 반환합니다. 이는 이진수에서 1비트를 왼쪽으로 이동시키는 것과 같습니다.
하지만, y가 홀수라면, 이전에 계산된 z를 2배하고 x를 더하여 반환합니다. 이는 y를 2로 나눈 몫과 1을 각각 2배한 후, x와 곱한 값과 같습니다.
- Two n-digit integer multiplication 두 개의 n자리 정수를 곱하는 것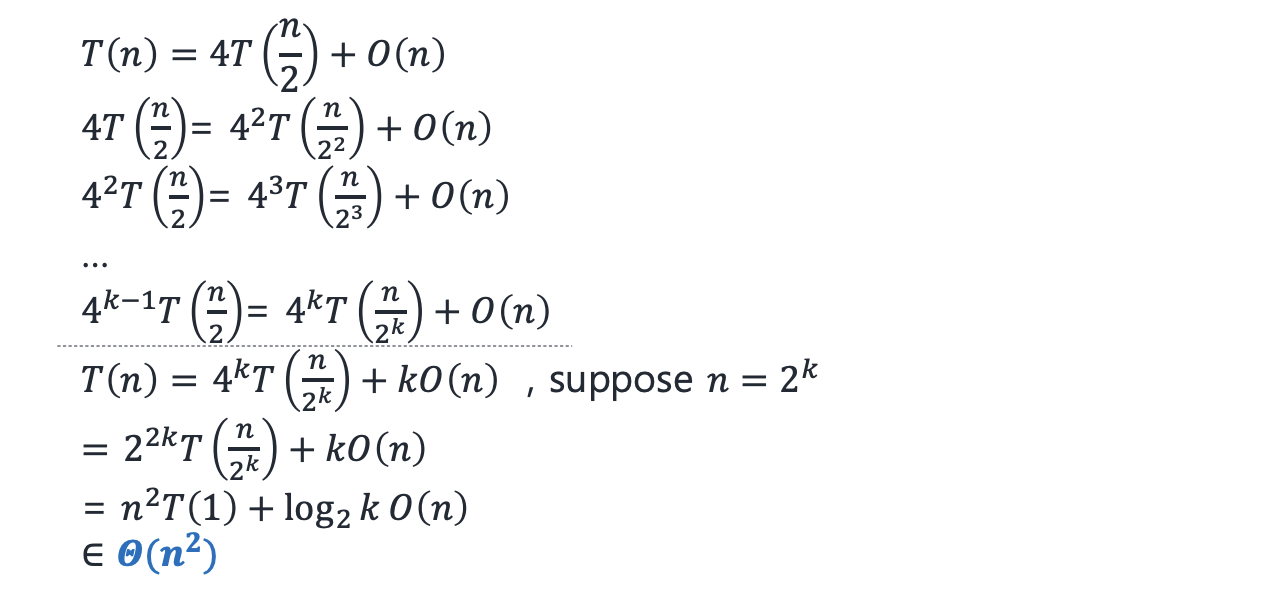
- Karatsuba multiplication
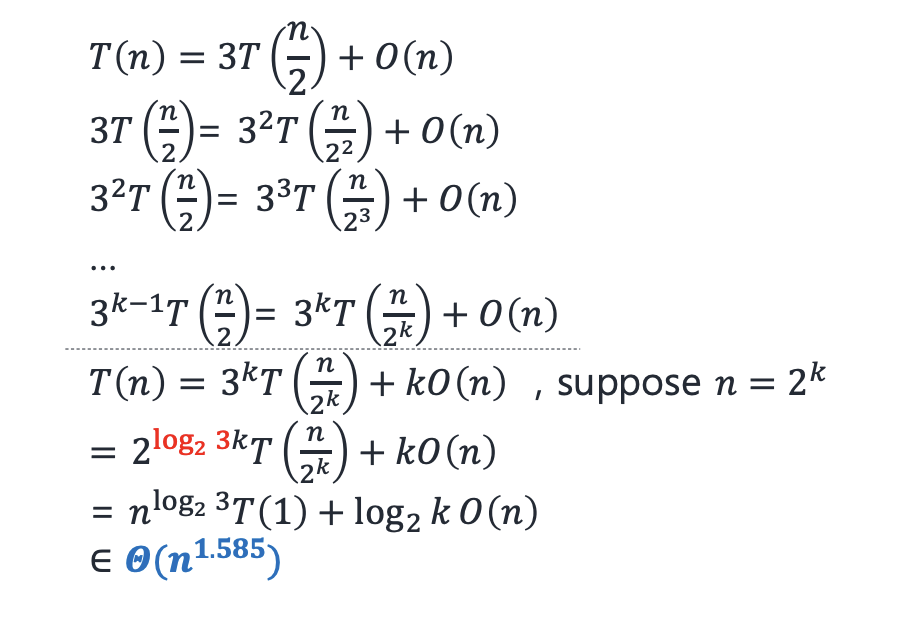
- Divide and conquer 방식의 곱셈은 큰 문제를 작은 문제들로 나누어 해결하는 알고리즘입니다. 예를 들어 두 개의 n자리 수를 곱할 때, 이를 n/2 자리 수의 문제들로 나누고 이를 재귀적으로 해결하는 방식입니다.
- Karatsuba 곱셈은 divide and conquer 방식을 사용하는 특정한 알고리즘으로, 두 수를 세 부분으로 나누어 문제를 해결합니다. 그리고 (a + b)(c + d) = ac + bd + (ad + bc) 공식을 이용하여 두 자리 수의 곱셈을 세 번의 곱셈으로 계산합니다. 이 방식으로 생성되는 subproblem의 수를 줄이기 때문에, 큰 수를 곱할 때 빠른 결과를 얻을 수 있습니다.
Modular exponentiation
: it is necessary to compute ( x^y mod N ) for large values of x, y and N that are several hundred bits long
 --> Let x, y and N be n-bit numbers. Total running time O(n^3) -bit operations
--> Let x, y and N be n-bit numbers. Total running time O(n^3) -bit operations
Matrix multiplication
 T(N) = N^3T(1) + log2(N)O(n^2) ∈ Θ(n^3)
T(N) = N^3T(1) + log2(N)O(n^2) ∈ Θ(n^3)
- Strassen’s algorithm
 T(n) ∈ Θ(n^log2(7)) = Θ(n^2.81)
T(n) ∈ Θ(n^log2(7)) = Θ(n^2.81)
Merge sort
: Merging (two-way merging): Combining two sorted lists into one
sorted list , Divide and conquer approach
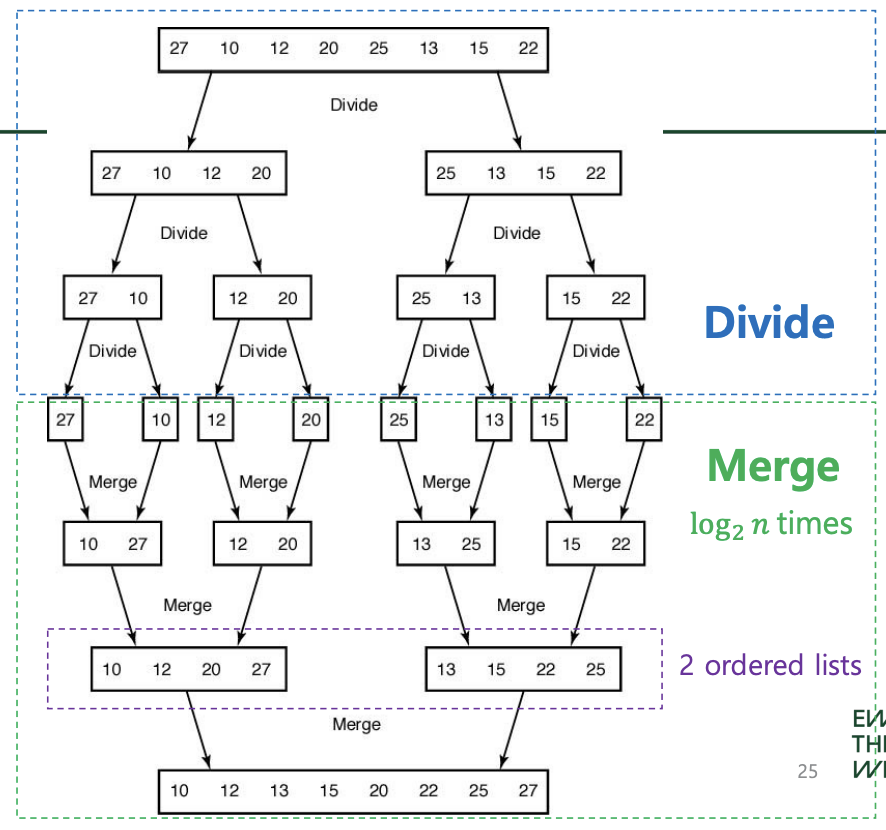

worst case: len(left_arr)+len(right_arr)-1 =h+m-1
T(n) = nT(1) + log2(n(n − 1)) ∈ Θ(nlog(n))
Better approach for merge sort
Quick sort
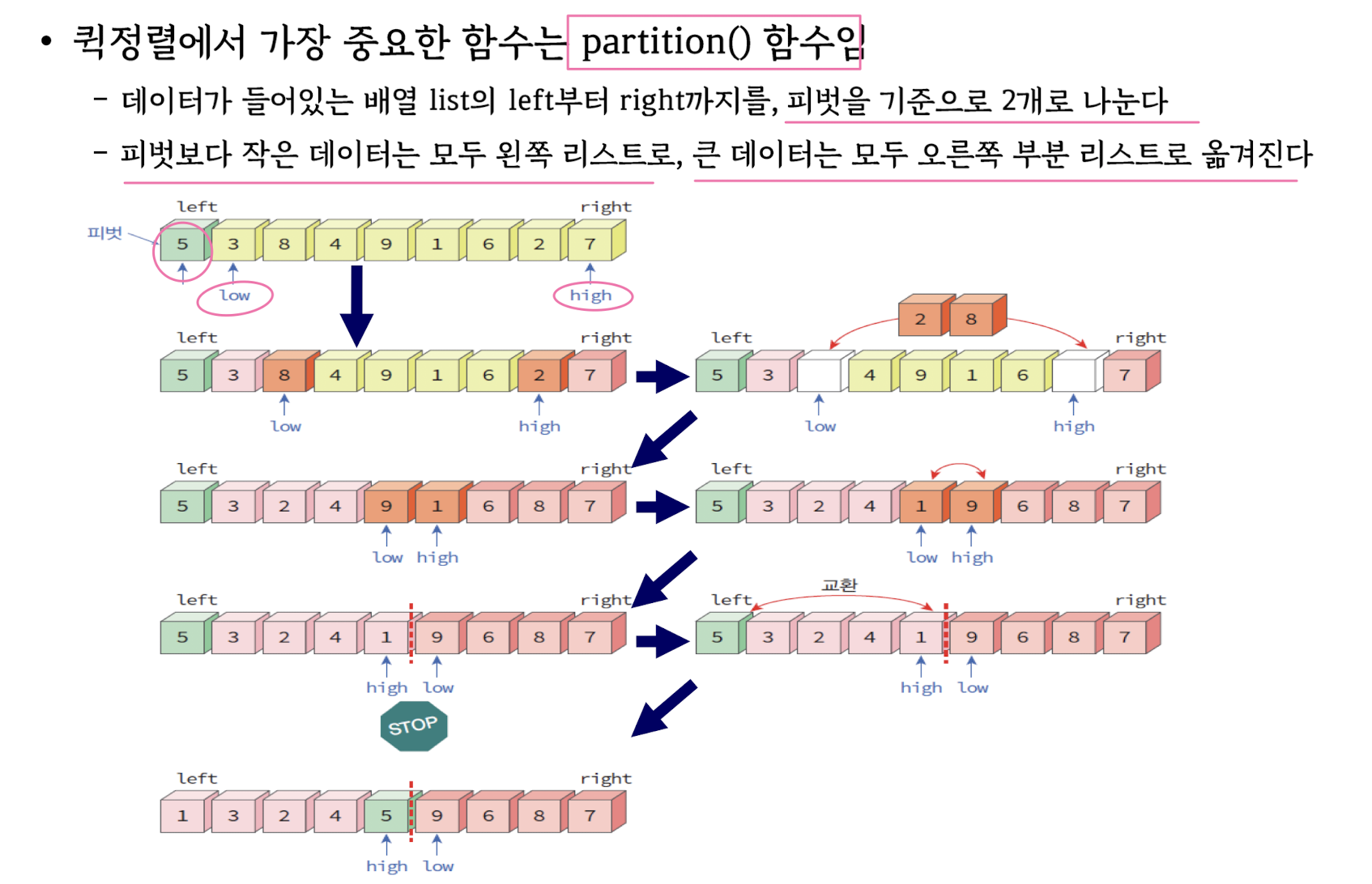



T(n) = 2T(n/2) + O(n) ∈ Θ(nlog(n))
When the pivot is picked using MAX and MIN (worst-case) ∈ Θ(n^2)
3. Greedy Algorithm
"locally optimal choice"
It starts with an empty set and adds items to the set in sequen
ce until the set represents a solution. Each iteration consists of
1. Selection procedure: Add the next item to the set according to the locally optimal choice criteria.
2. Feasibility check: Check if the new set is feasible and constitutes a solution to the instance.
Find minimum number of coins for change
• Time complexity: Θ(n)
• Greedy method does not always give an optimal solution
• Better approach (Dynamic programming)Matrix-chain product

But, this problem can be solved with dynamic programming
approach to get an optimal solution in general case
Graph coloring

adj_colors 변수는 현재 선택된 정점 u의 인접 정점들 중에서 이미 색칠된 정점들의 색상 집합이 됩니다.
- Two isomorphic graphs can heave different x(G) if we number nodes dfferently
- Graph coloring applications : Scheduling (assignment2)
```
# 그래프 구현
graph = {
'Culture': ['Defense', 'Education'],
'Defense': ['Culture', 'Foreign Affairs', 'Justice', 'Technology'],
'Education': ['Culture'],
'Food Affairs': [],
'Foreign Affairs': ['Defense'],
'Justice': ['Defense'],
'Technology': ['Defense']
}
# 노드의 색상을 저장하는 딕셔너리
colors = {}
# 가능한 색상의 목록
available_colors = ['red', 'blue', 'green', 'yellow']
# 각 노드에 대해 색상을 선택
for node in graph.keys():
# 해당 노드에 인접한 노드들의 색상을 조회하여 사용 중인 색상을 가져옴
used_colors = set([colors.get(neighbour) for neighbour in graph[node] if neighbour in colors])
# 가능한 색상 중 사용 중인 색상을 제외하고 최소한의 색상을 선택
for color in available_colors:
if color not in used_colors:
colors[node] = color
break
# 필요한 최소 시간 슬롯의 수 계산
num_time_slots = len(set(colors.values()))
# 결과 출력
print(f"필요한 최소 시간 슬롯의 수: {num_time_slots}")
print(f"노드별 색상: {colors}")
```
> 필요한 최소 시간 슬롯의 수: 4
노드별 색상: {'Culture': 'red', 'Defense': 'blue', 'Education': 'red', 'Food Affairs': 'red', 'Foreign Affairs': 'blue', 'Justice': 'yellow', 'Technology': 'green'}Minimum spanning trees (MST)
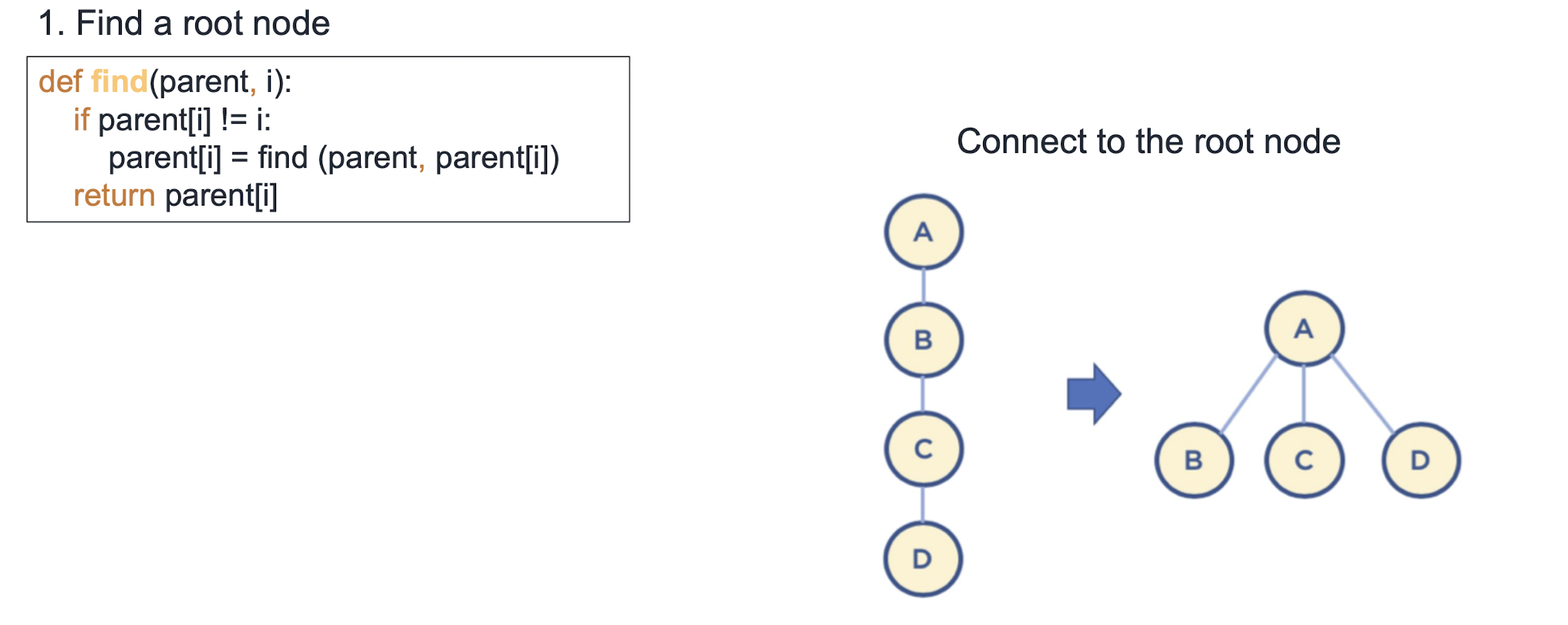
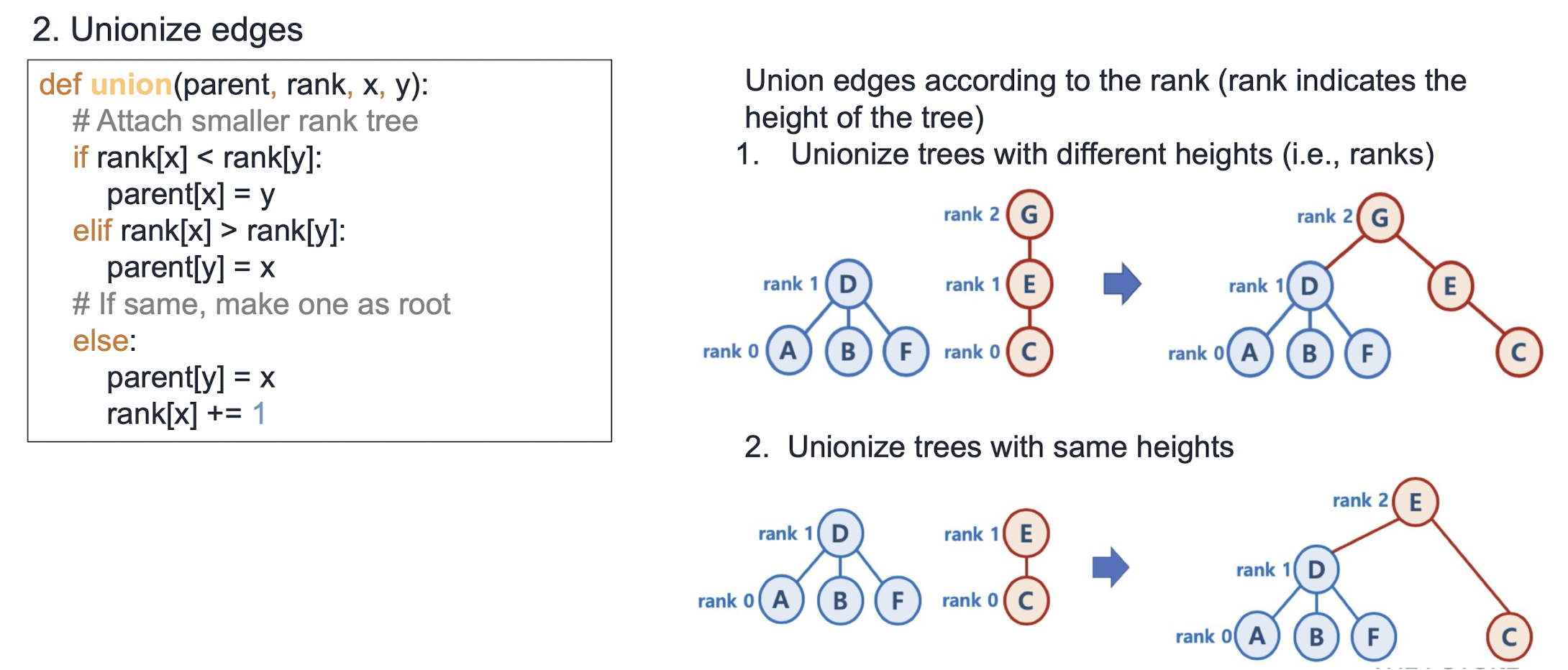
- **Spanning tree**: all nodes are connected and acyclic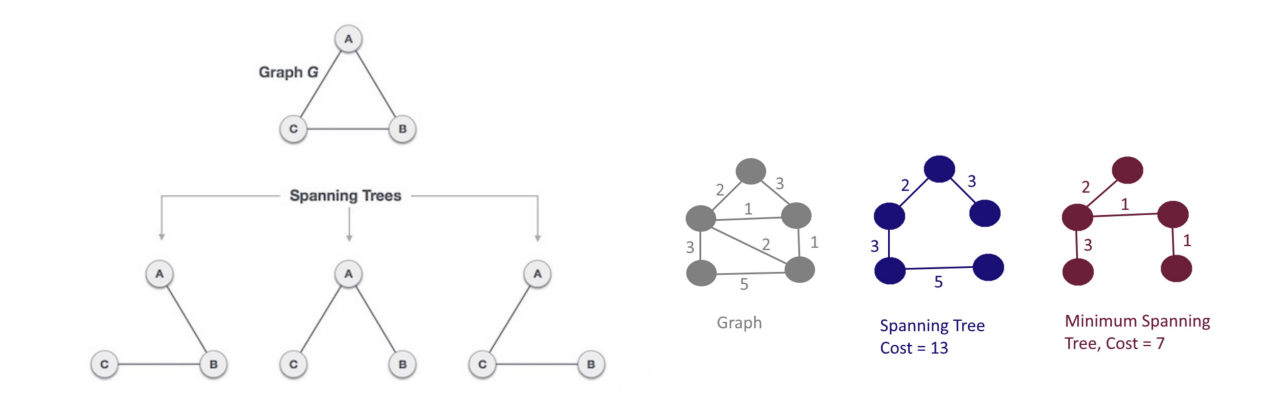
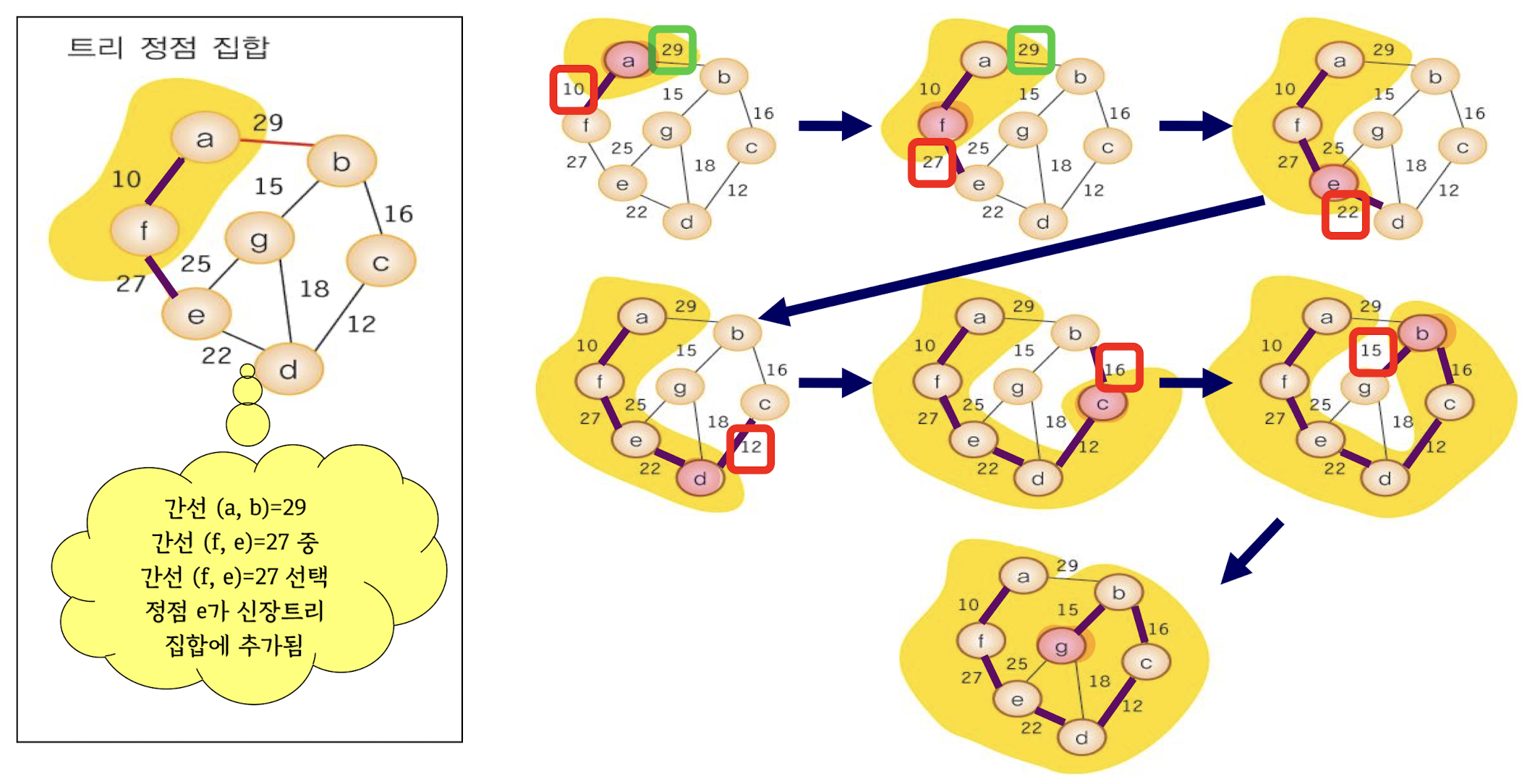
MST – Prim’s algorithm
시작점에서 출발하여, 이미 선택된 노드와 연결된 가장 적은 비용의 간선을 선택
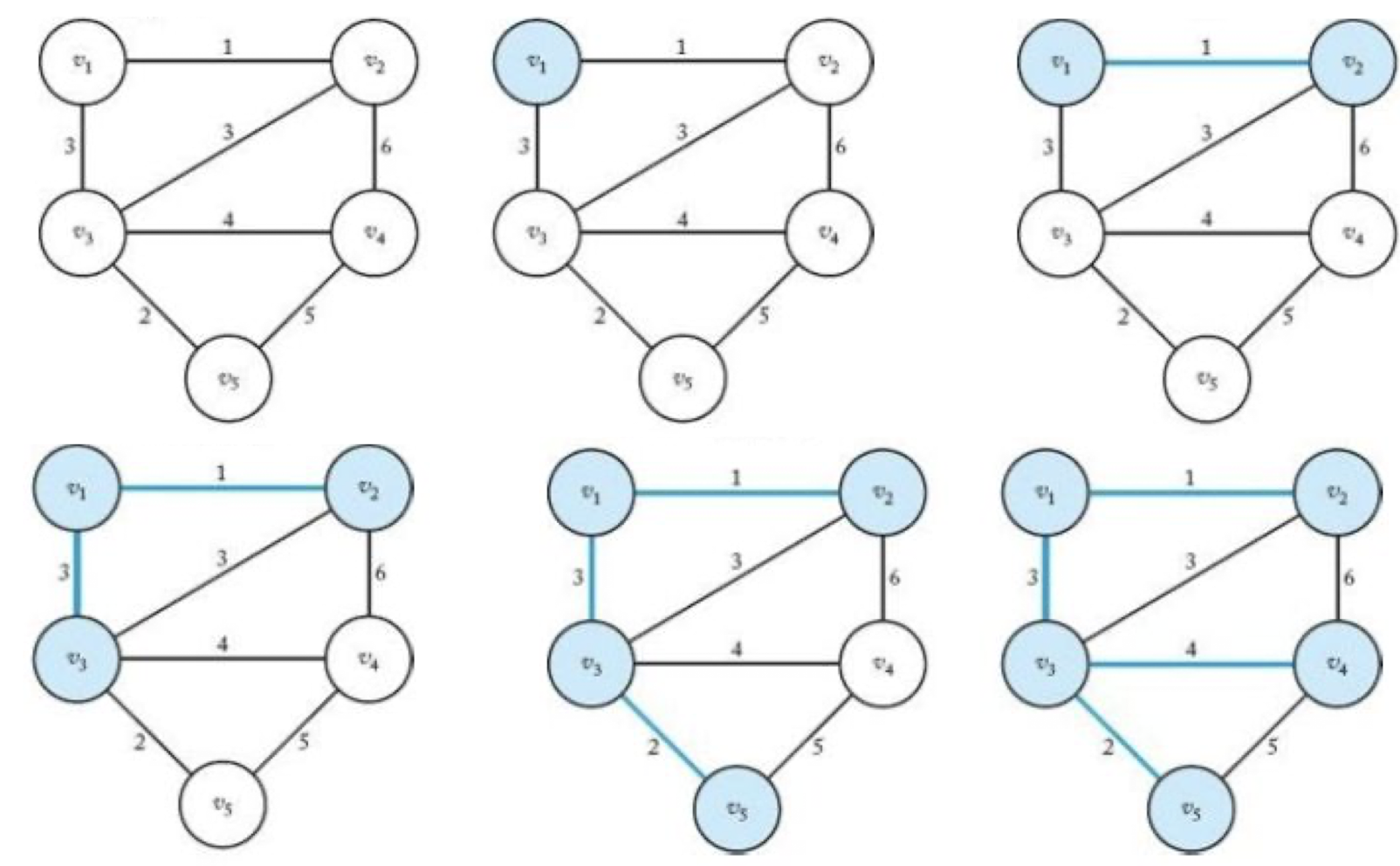
MST – Kruskal's algorithm
모든 간선을 비용이 적은 순서대로 정렬한 후, 가장 작은 비용의 간선부터 하나씩 선택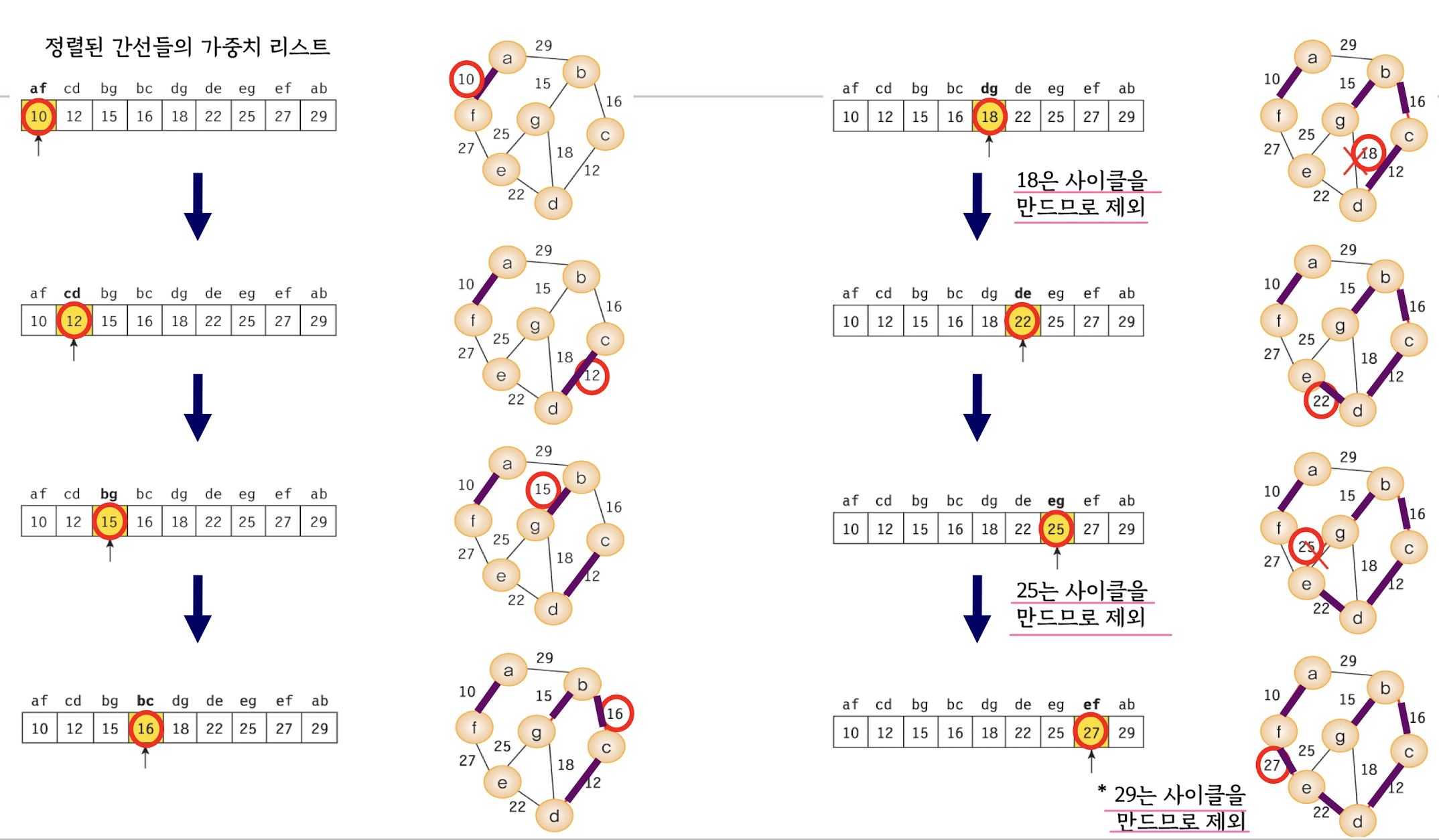

- graph = sorted (graph,key=lambda item: item[2])
=> graph 리스트의 요소들은 각각 (노드1, 노드2, 가중치) 형태로 되어 있으며, 이중 튜플의 세 번째 값인 가중치를 기준으로 정렬.

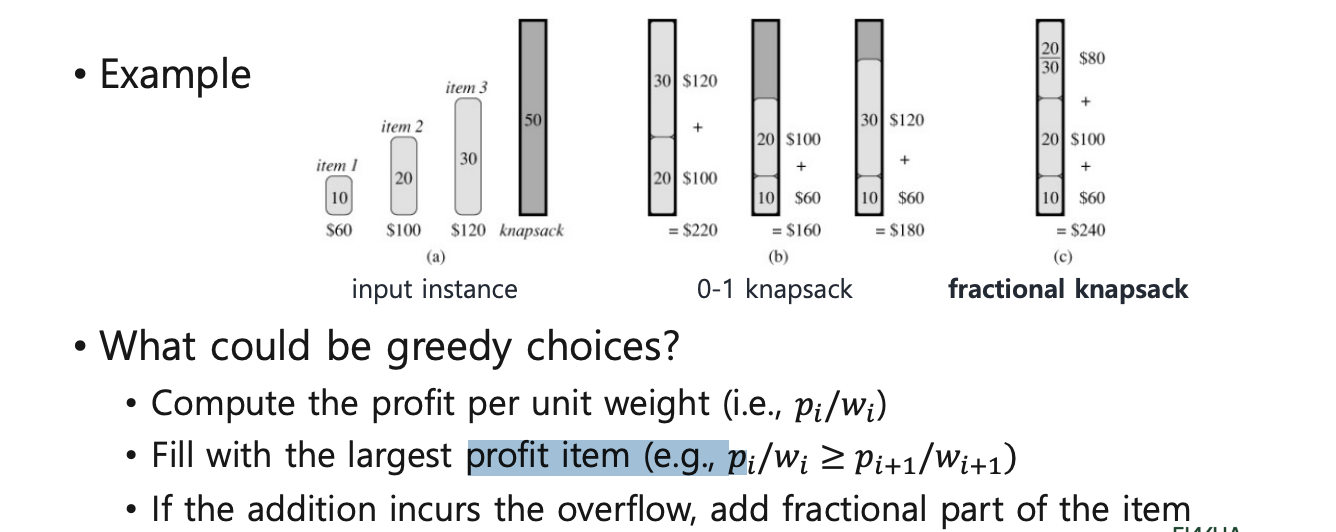
Fractional knapsack

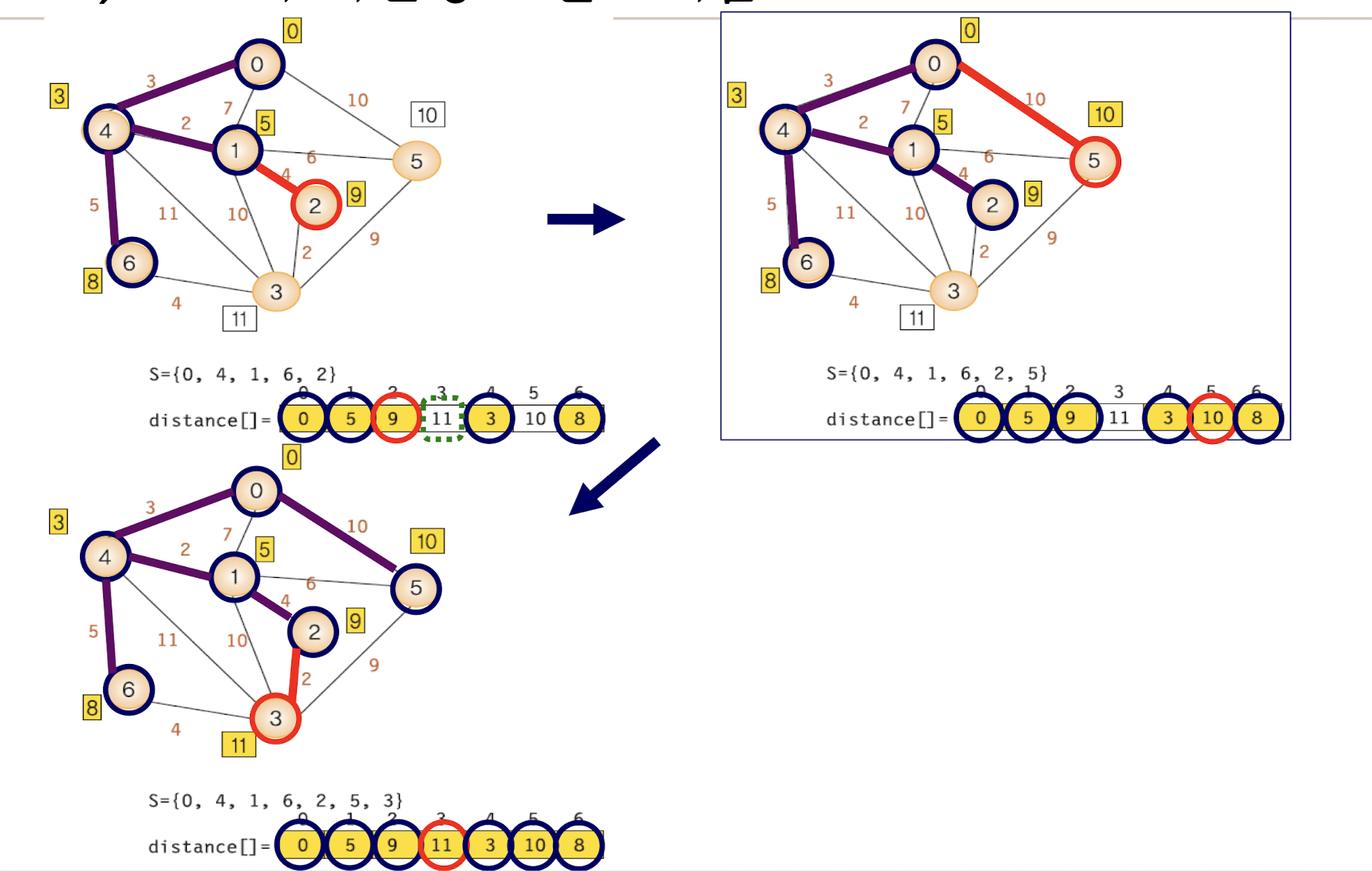
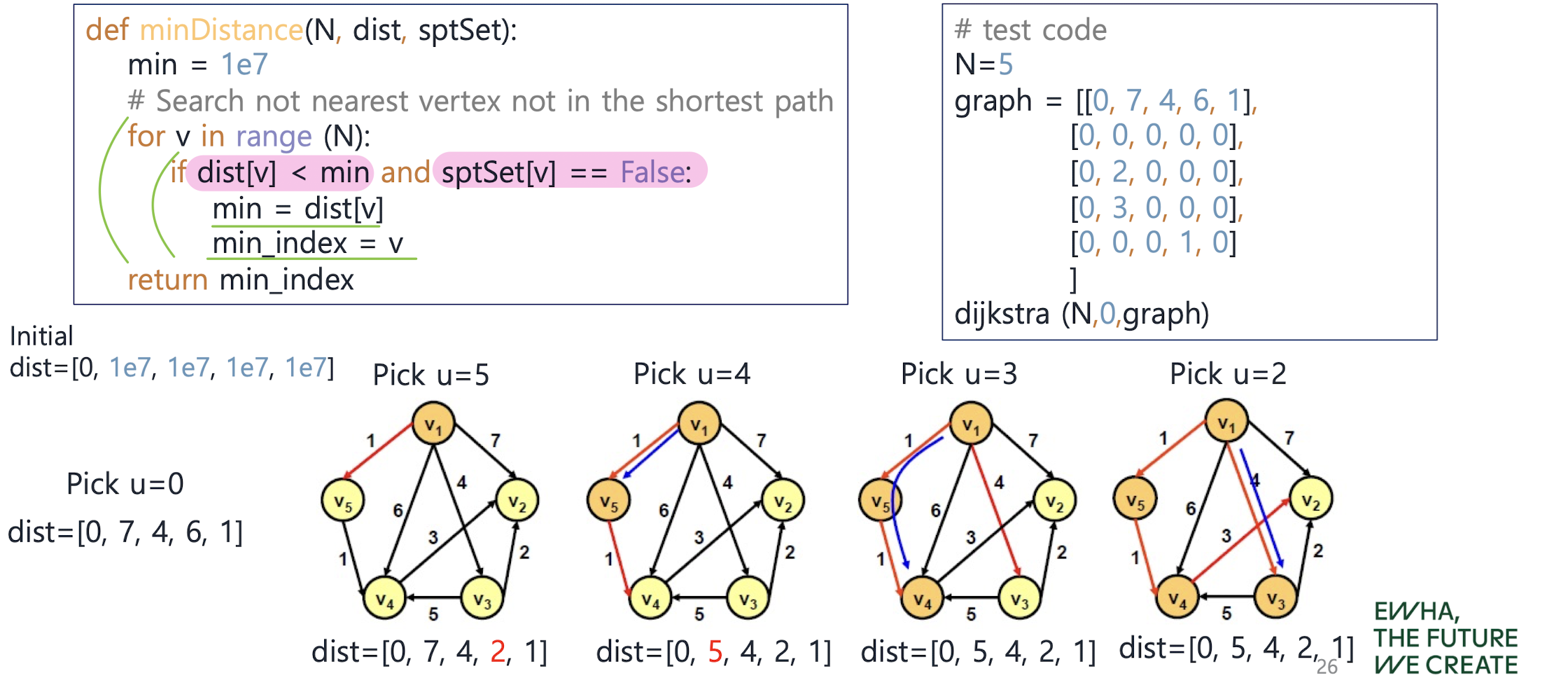
Shortest Paths - Dijkstra's Algorithm
: 하나의 정점에서 출발해서 다른 모든 정점으로의 최단 경로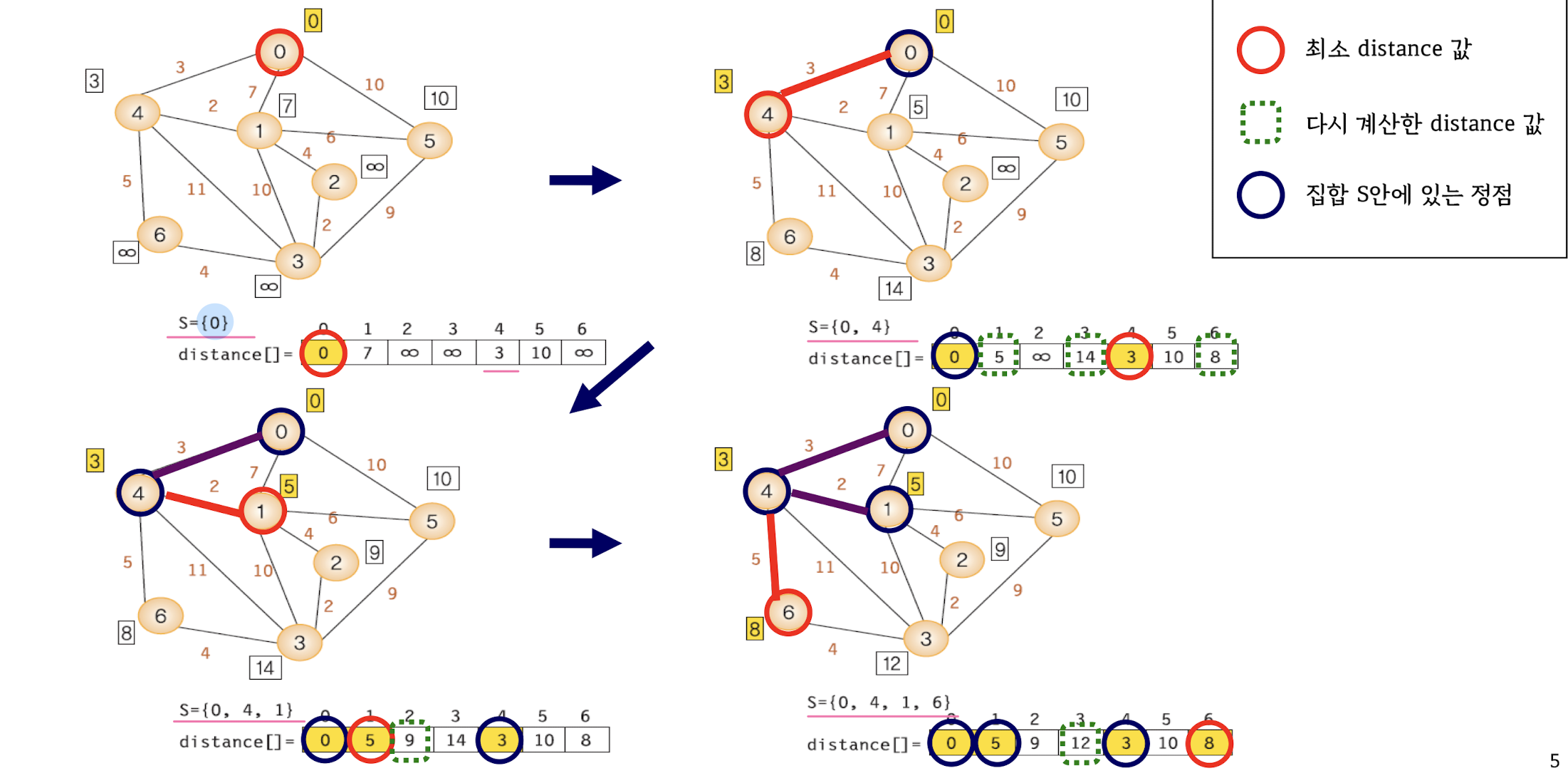

Huffman code
: to find a binary character code for the characters in a file, which represents the file in the least # of bits

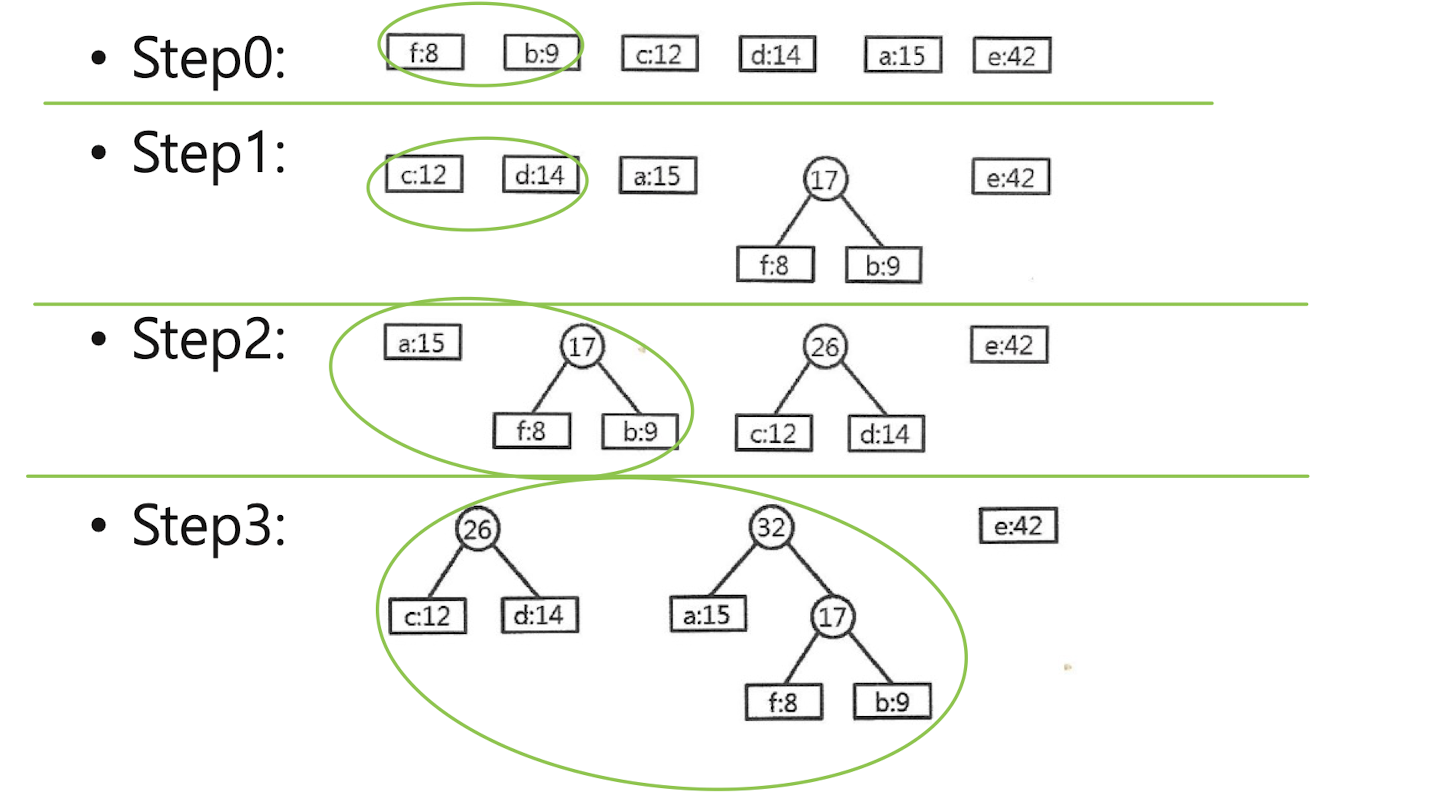
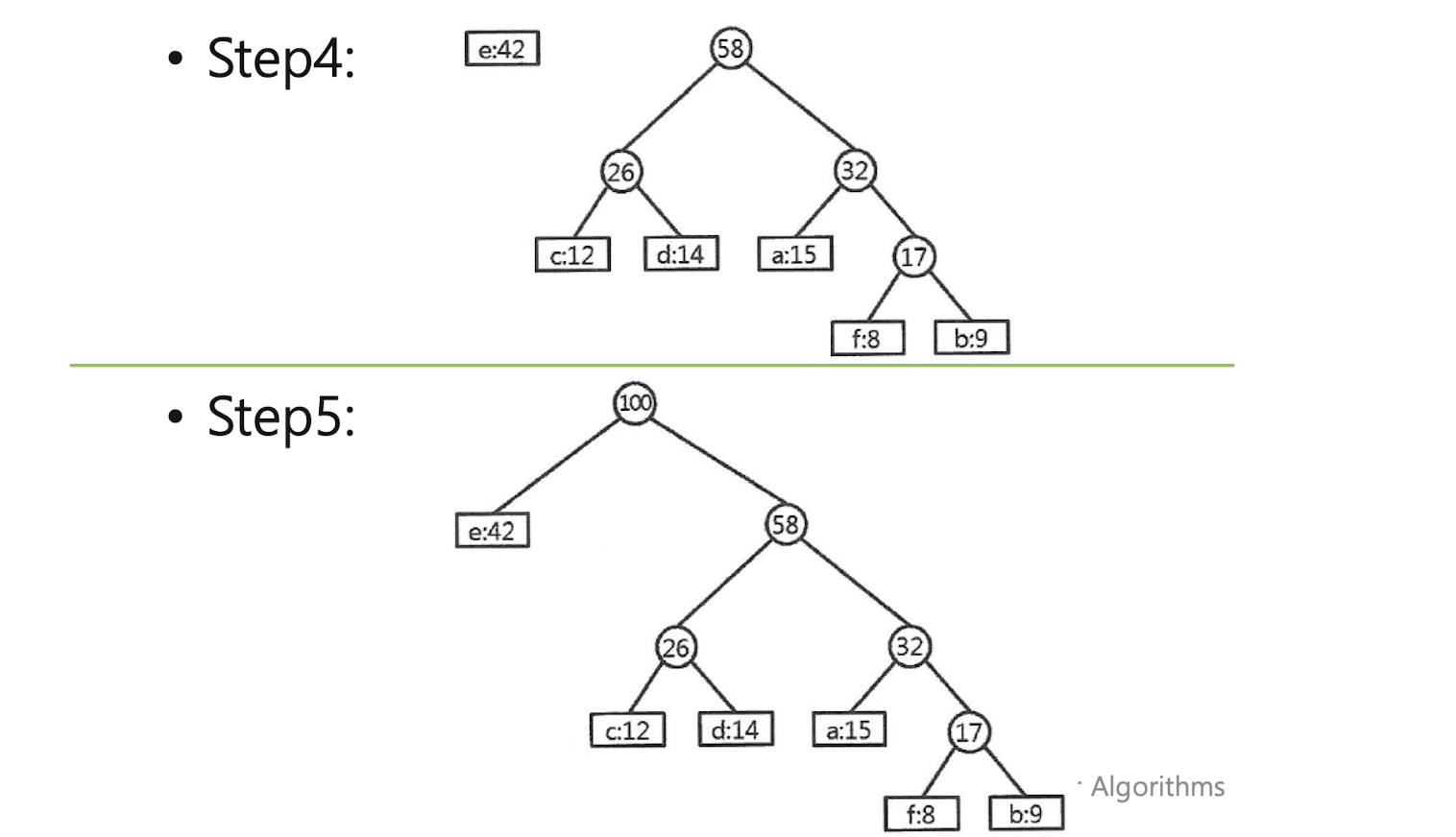

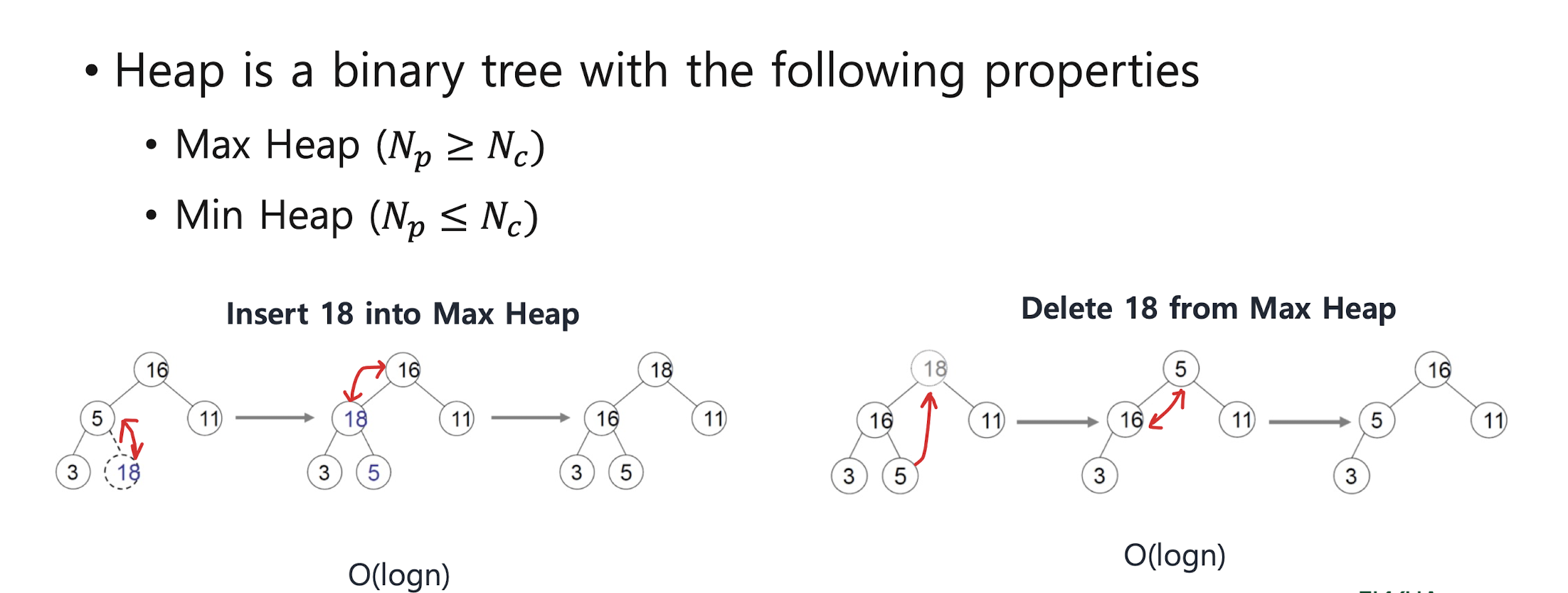
* Heap
4. Dynamic Programming
Dynamic programming
" bottom up approach "
1) Establish the recursive property
(2) Solve instances of the problem in a bottom-up fashion by solving smaller instance first and keep a table of known results.
(3) Reuse the result from the table, if necessary.
Binomial coefficients


ex)Pascal’s Triangle: P[i][ j]=P[i][ j-1]*(i-( j-1))//( j-1)

Longest increasing subsequence
 ->the longest increasing subsequence is (2, 3, 4) or (2, 3, 6)
->the longest increasing subsequence is (2, 3, 4) or (2, 3, 6)
 Time complexity: 𝑂(𝑛^2)
Time complexity: 𝑂(𝑛^2)
Space complexity: 𝑂(𝑛)
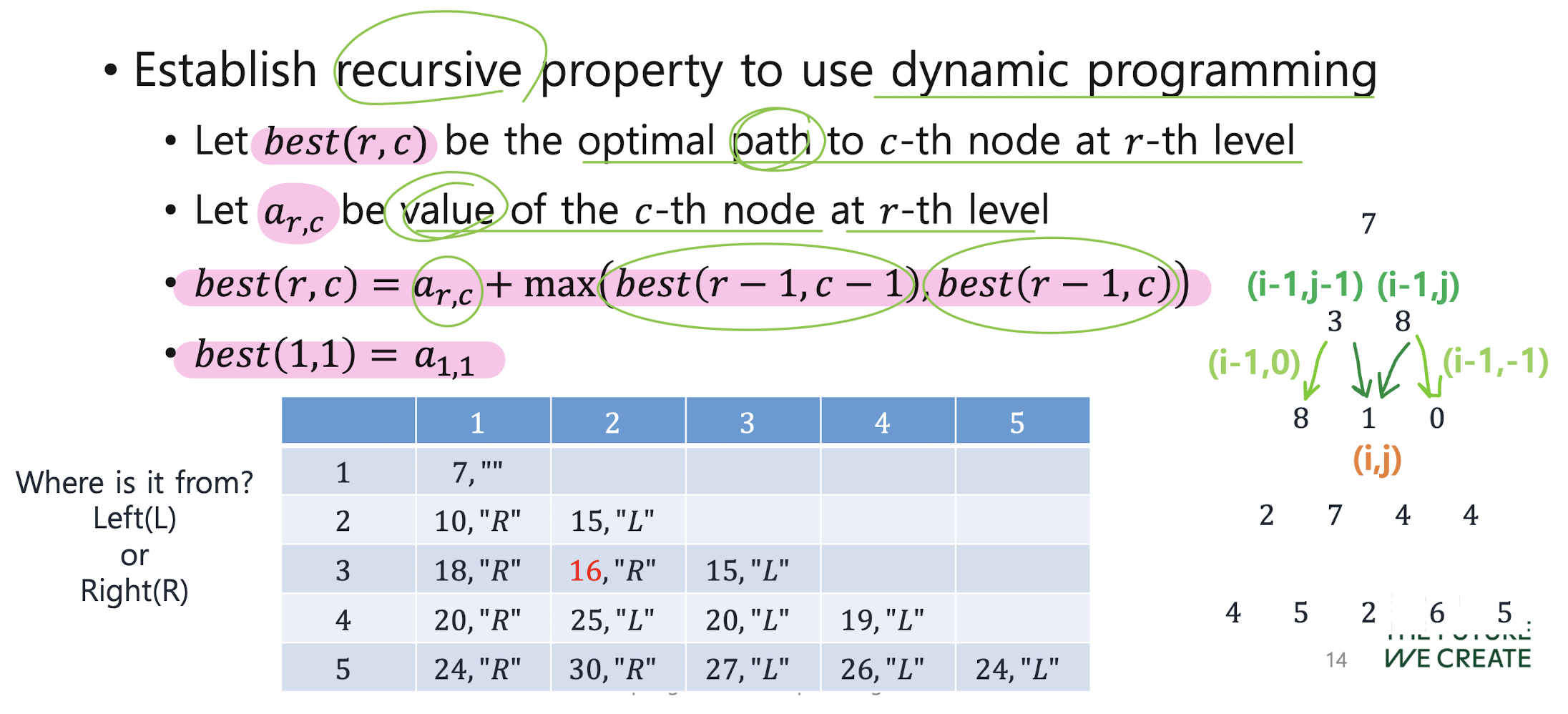
Number triangles
: find the maximum sum of numbers passed on a route that starts at the top and ends somewhere on the base.
Each step can go either diagonally down to the left or diagonally down to the right.
- Assume that we do exhaustive search (i.e., look into all pos sible paths)
-> Time complexity: Θ(2^k) = Θ(2^sqrt(n))


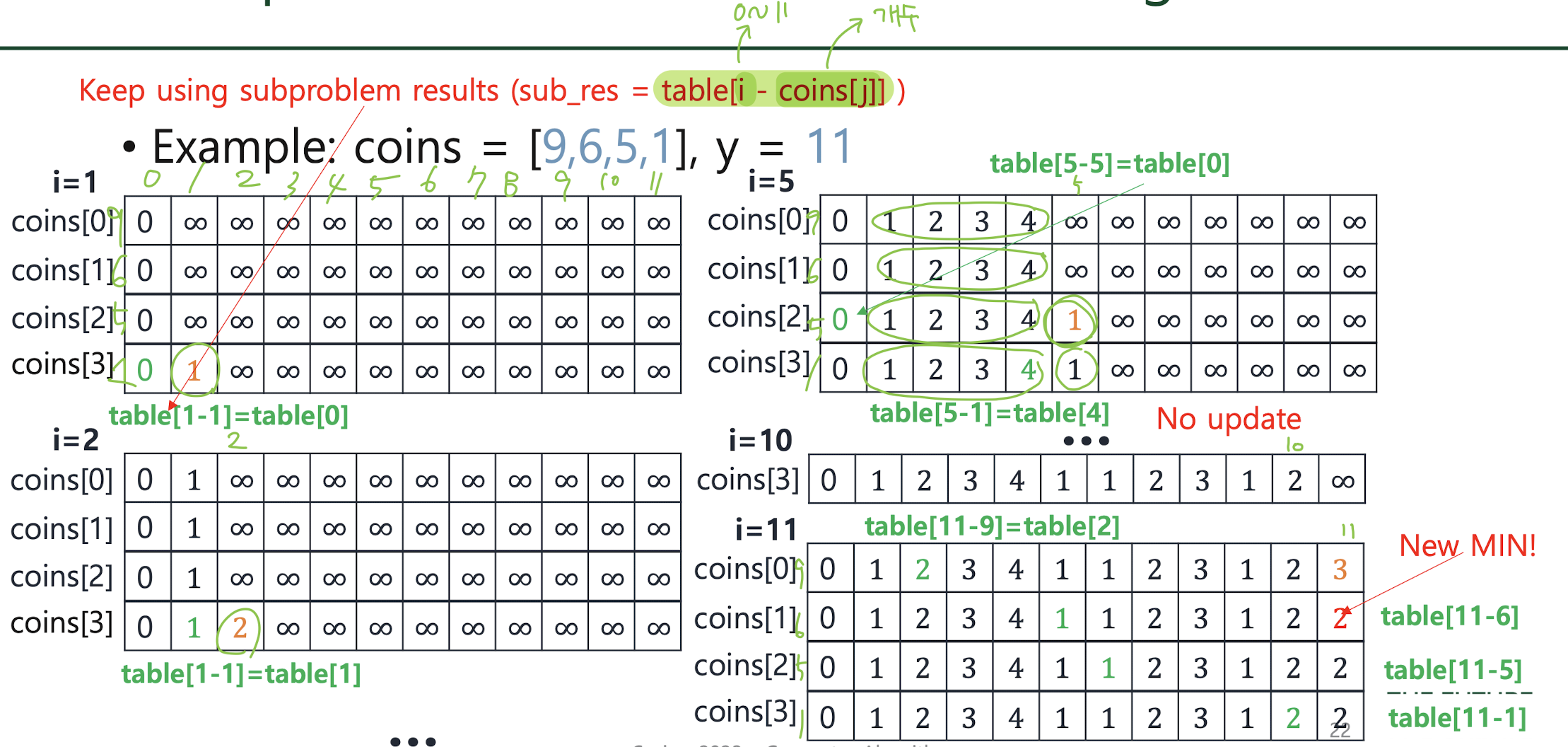
Revisit minimum coin change
 -> Time complexity: O(my) Space complexity: O(y)
-> Time complexity: O(my) Space complexity: O(y)
Revisit chained matrix multiplications
to determine the best order for multiplying 𝑛 matric es, 𝐴 = 𝐴1×𝐴2×...×𝐴"
- Catalan numbers (=The number of different orders)
the n-th Catalan number, C(n) = (2n)! / (n+1)!n!
연쇄행렬곱셈에서 가능한 경우의 수...지수함수...ㅠㅠ
그래서!
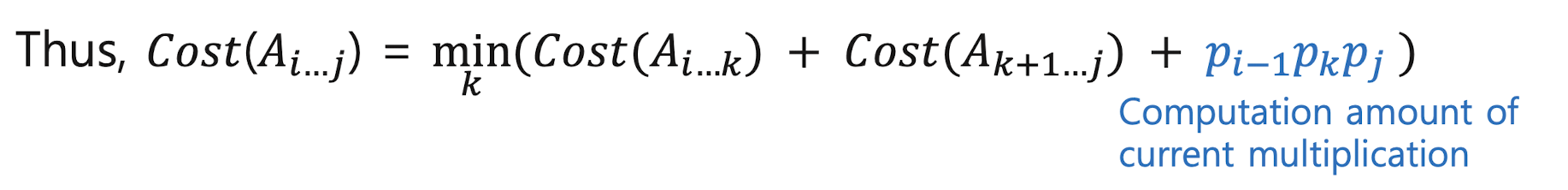
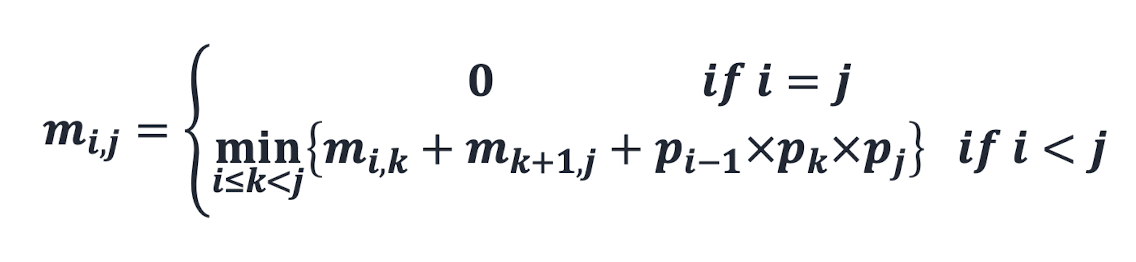 the minimum # of number multiplications to compute Ai × ... × Aj, 1 ≤ 𝑖 ≤ 𝑗 ≤ 𝑛.
the minimum # of number multiplications to compute Ai × ... × Aj, 1 ≤ 𝑖 ≤ 𝑗 ≤ 𝑛.
= 각 부분 행렬의 곱셈 횟수 + 두 행렬의 곱셈 횟수
 각 부분 행렬의 곱셈 횟수 + 두 행렬의 곱셈 횟수
각 부분 행렬의 곱셈 횟수 + 두 행렬의 곱셈 횟수

Time complexity: O(𝑛^3)
Space complexity: O(𝑛^2)
Edit distance
: the minimu m # of edit operations (insertions, deletions and substitutions) need ed to transform the first sequence S to second sequence T
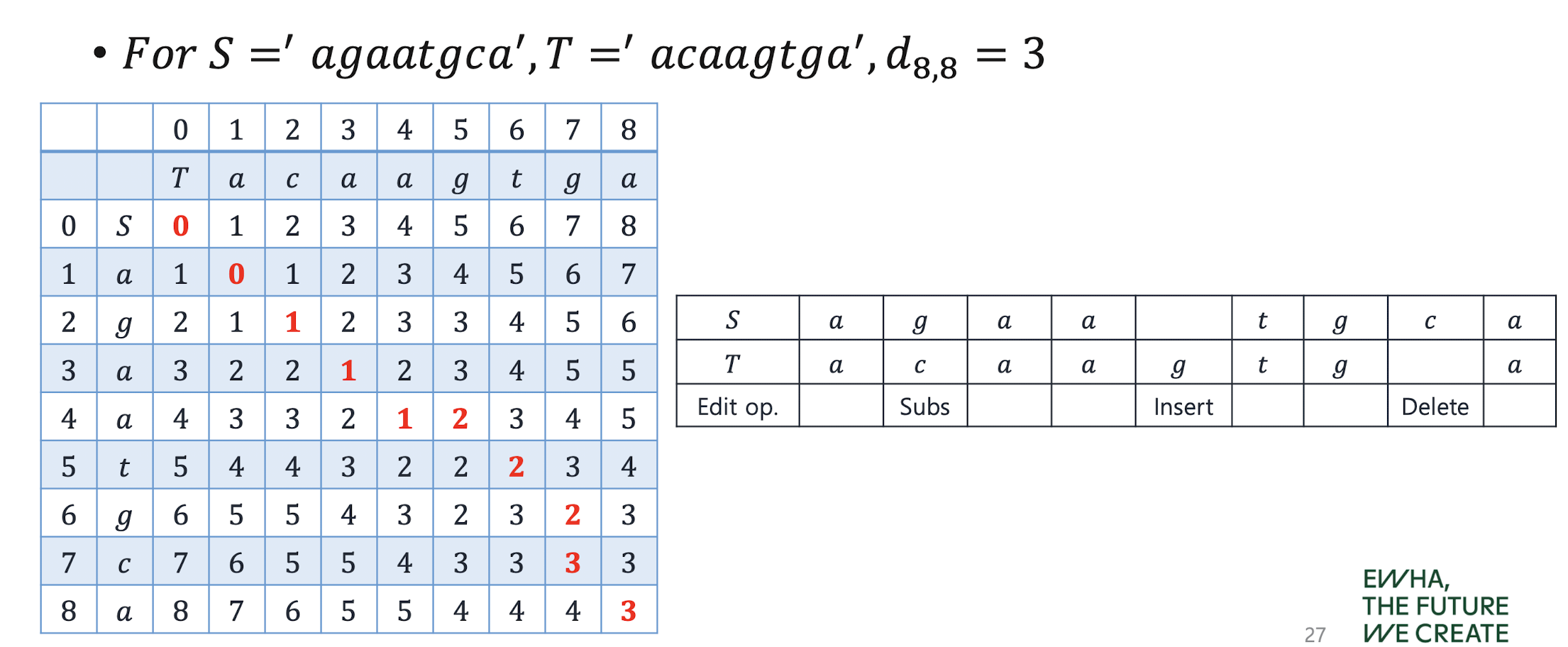
Step1. Create the table with rows (‘ ‘, ‘c’, ‘a’, ‘t’) and columns (‘ ‘, ‘c’, ‘a’, ‘k’, ‘e’) and compute edit distance when one side is null
Step2. If the characters are same, take the value on left above
Step3. For other cases, take the minimum on values on left-above, left, and above and then increment by 1

Optimality Principle
: to apply in a problem if an opti mal solution always contains optimal solutions to all subinstances.
ex) the shortest path sum problem O , but the longest path sum problem X
Floyd-Warshall's Algorithm for All-Pair-ShortestPath Problem
: 모든 정점에서 다른 모든 정점으로의 최단 경로
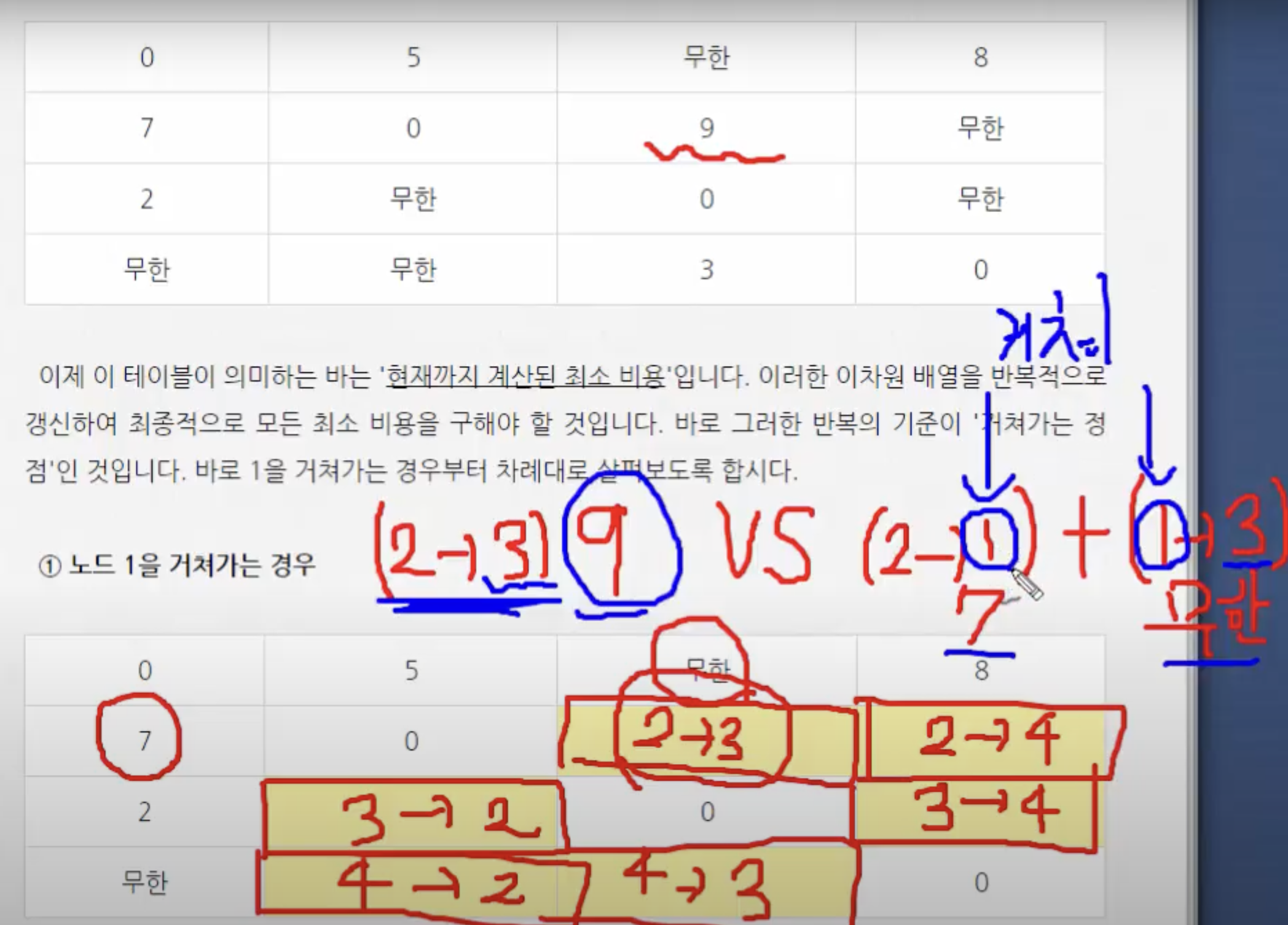
: finding s hortest paths between all pairs of vertices
: to compute by matrix D, where dij = the distance (sho rtest path) from vi to vj for all i, j.
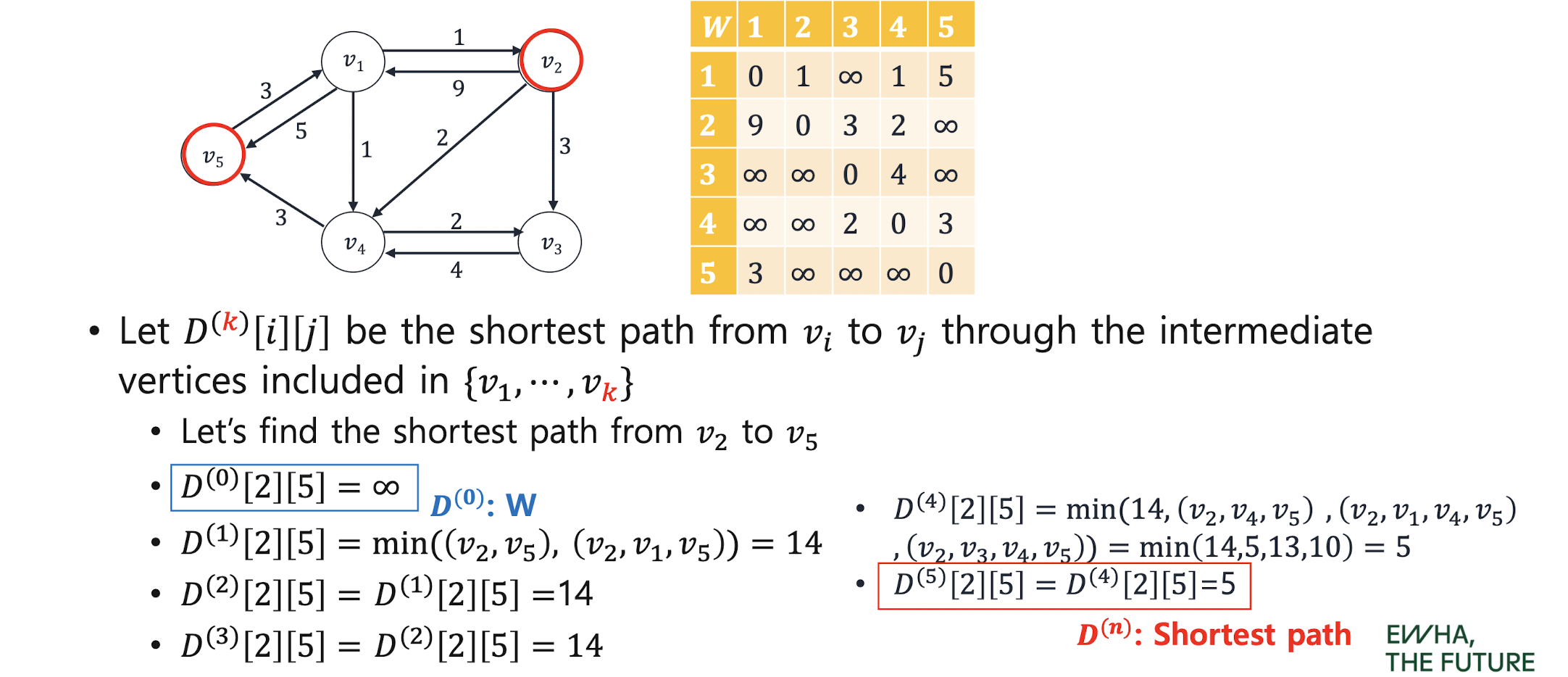

0-1 Knapsack Problem
Optimal solution: 𝐾[𝑛, 𝑀] = max { K[i-1,w] , K[i-1,w-𝒘𝒊]+ 𝒑𝒊 }
Maximum profit when considering item 1 ∼ (𝑖 − 1) and knapsack capa is 𝑤

5. NP problems & Approximation Algorithms
Realistic / Unrealistic algorithms
-
realistic: execution cost (complexity) is a constant power 𝑛+ of the size of its inputs 𝑛. (polynomial complexity)
-
unrealistic: the running cost (complexity) of an algorithm rises exponentially above a constant (𝑘^n)
-
P: Problems that can be solved at a realistic cost, that is, have polynomial time algorithms
-
Efficiency : can be achieved only by polynomial algorithms and should have very low degree
(e.g., 𝑂(𝑛^3) could not be efficient) -
Difficulty : “difficult to solve with computers
Tractable/ Intractable problems
-
polynomial-time algorithm : whose worst-case time c omplexity is bounded by a polynomial function of its input size .
Θ(1), Θ(logn), Θ(n), Θ(nlogn), Θ(n2), ... , Θ(nk) for some constant k (that is, O(n^k)) -
Super-polynomial time algorithms : Θ(2^k), Θ(n!), ...
-
tractable : there is a polynomial time algorithm that solves it.
-
intractable : there is no polynomial time that solves it.
-
NP : problems sitting near the boundary between tractable and intractable problems
Non-deterministic algorithms
- deterministic algorithms : give n the same input, the same ou tput is always guaranteed
- Non-deterministic algorithms : not guaranteed to give the same output
일단 답 도출하고 맞는지 체크-> ploynomial time이면 그래도 괜찮다. NP다.
Once we solve it, the verification is NOT that difficult.
(1) Guessing (Non-deterministic) stage: Given an instance of a problem, this stag e produces a guess at a solution to the instance.
(2) Verification (Checking) stage: The solution guessed in the guess step is checked by an algorithm that determines whether it is the answer to the given problem.
Outputs Yes if the answer to the given question is correct, and No if not.
Polynomial-time non-deterministic algorithms
: Verification (checking) step can be performed in polynomial time.
- if someone claims to know the answer, then it can be done in polynomial time to check if that person's claim is correct.
- It does NOT mean that the optimal solution can be found in polynomial time
답인지 아닌지 체크는 쉽게 하지만, 솔루션은 어려워
P, NP
-
NP : the set of all “decision problems” that can be solved by polynomial- time non-deterministic algorithms.

-
Mostly, problems dealt with in P and NP theory are limited to decision problems.
-
An optimization problem can always be transformed into a corresponding decision problem.
• Optimization problem : a problem with an optimal value of given cost function
• Decision problem: a problem with a yes/no answer. -
General categories of problems
• Problems for which polynomial-time (or “efficient”) algorithms have been found (e.g., sorting problem)
• Problems that is intractable, with no polynomial-time algorith ms have never been found (e.g., 0-1 knapsack problem)
• Problems that is undecidable (e.g., the halting problem)
NP examples
- searching

- Traveling salesman problem (TSP)
- Graph coloring

- Hamiltonian Cycle

- Subset Sum

- Bin packing

- CNF Satisfiability (decision problem only)

P vs NP
- P ⊆ NP
- To show that P≠NP, we would have to find a problem in NP that is not in P, whereas to show that P= NP, we would have to find a polynomial-time algorithm for each problem in NP.
- One of 7 millennium problems provided by Clay Mathematics Institute. 한개만 해결됨
정리 설명!!!
Problem transformation(reduction)
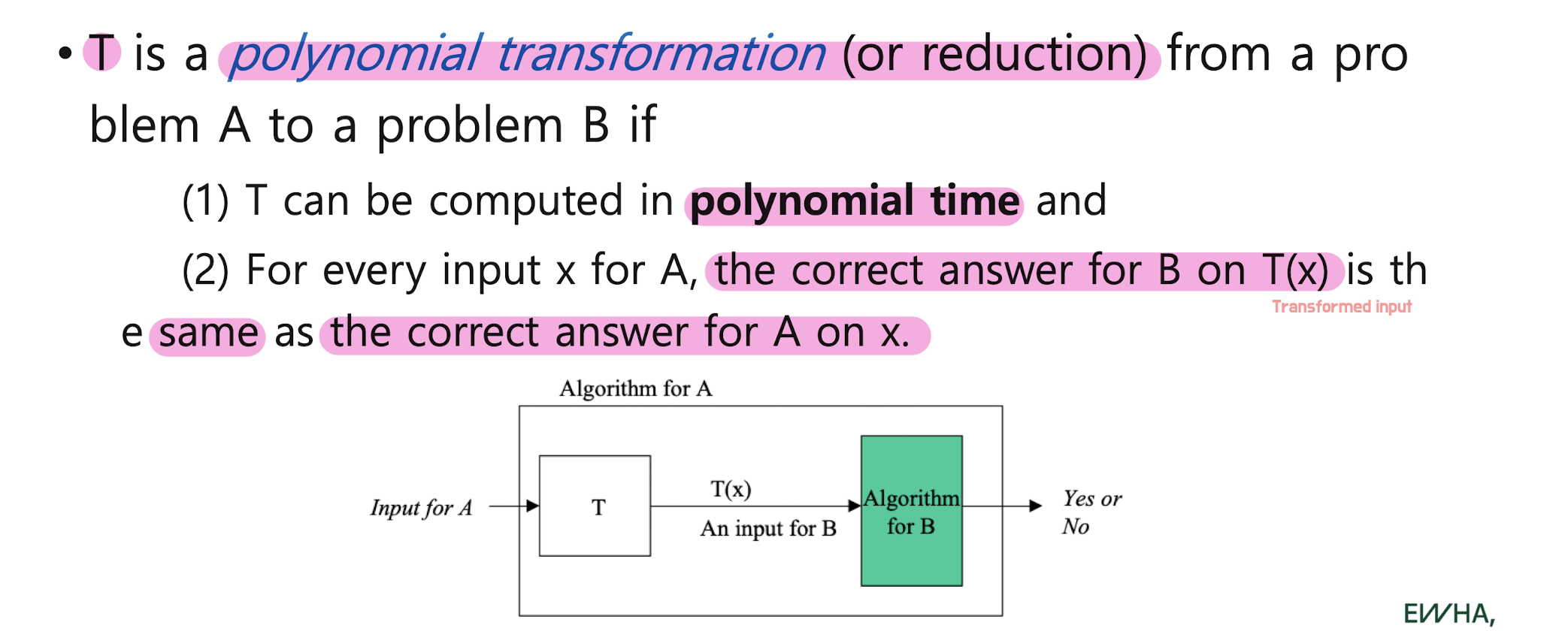

input을 바꾸는 과정이 쉽게 이루어져야 한다. input transformation
모든 인풋이 변화하지 않은 인풋에 대해서 같은 결과......
NP-complete
-
A problem A is polynomially transformable to B if there is a polynomial transformation from A to B. Then, we write A ∝ B.
np에는 속하는데 좀 어려운 특별한 그룹. np에 속하지만 좀더 제한된 그룹.
1. np 속함. 2. 관련있는 np complete 문제 뽑아서 .. -
If A ∝ B and B ∈ P, then A ∈ P. (by transitivity)
-
NP-complete : it is NP and for every other problem 𝜫’ in NP, 𝜫‘ ∝ 𝜫.
-
If any NP-complete problem is in P, then P = NP.
-
Cook’s theorem

NP-complete example
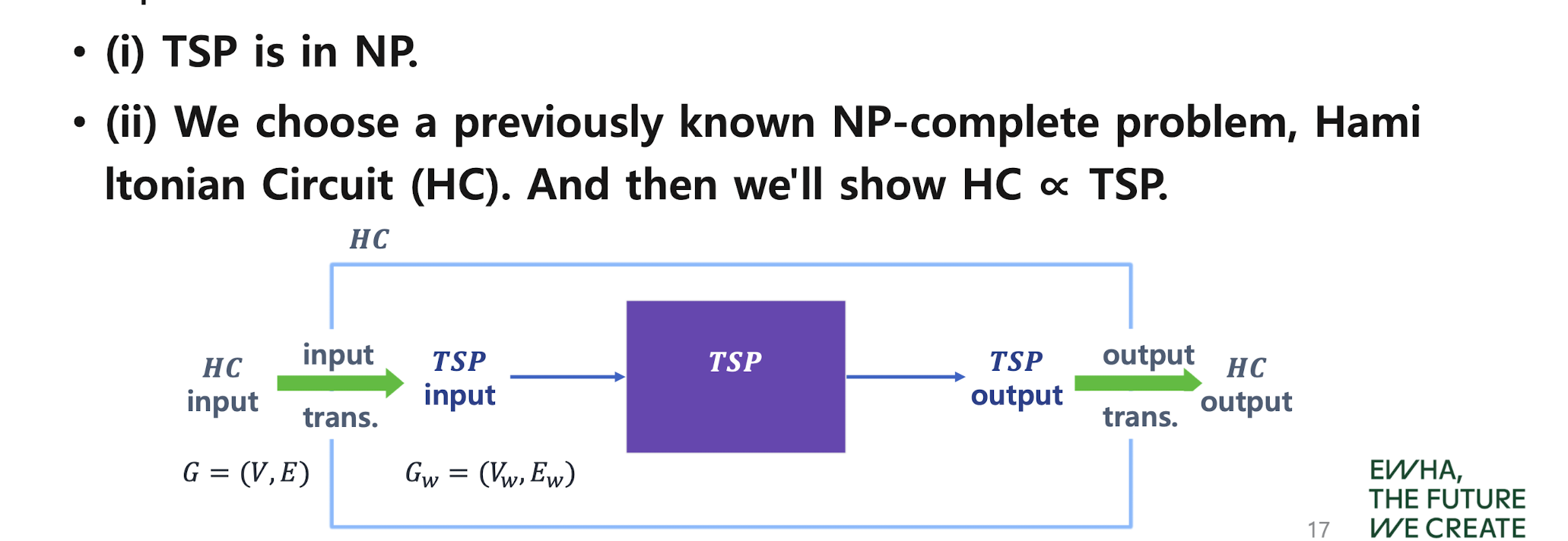
- Traveling Salesman Problem (TSP) problem

이 Salesman이 모든 집을 각각 한번씩만 방문하고,(= 방문 했던 집은 다시 방문 X) 이때 가장 짧은 경로(= 어떤 순서로 집을 방문해야하는지) 를 구하는 것이 TSP. 즉 외판원 문제입니다.
TSP는 보통 무향 완전 가중 그래프로 나타내지곤 하는데요, "완전"그래프이니 모든 집들 사이에 경로가 존재한다고 보면됩니다.
헤밀토니안 사이클이 뭔지 모르는 사람들을 위해 간단하게 설명드리자면,
주어진 그래프에서 출발점과 종료점만 두 번 나타나는 것을 제외하고는 정점이 한 번씩만 나타나는 사이클을 해밀턴 사이클 (Hamiltonian cycle) 이라고 합니다.
더 간단하게, "모든 노드들을 한번씩만 지나는 경로"라고 생각하시면 됩니다. (물론 Cycle이니 출발점과 종료점이 같아야겠죠? 이 사실은 잊지말아주세요 XD)
뭔가 TSP랑 비슷한 문제 같지 않나요?
실제로, TSP는
"가중치가 주어진 완전그래프에서 가장 작은 가중치를 가지는 헤밀턴 사이클을 구하라"라고 정의를 할 수 있답니다. 이건 Optimization버전이겠죠?
Decision버전은 "가중치가 주어진 완전그래프에서 가중치가 K인 헤밀턴 사이클이 존재하는가?"가 되겠네요.
Q : (무향 완전 가중 그래프를 주고) 이 그래프에서 모든 집을 한번씩만 방문하고 돌아나오는데, 그 가중치의 합이 K인것이 존재해?
자, 위 질문은 Certificate에 대해서 어떻게 대답할 수 있을까요?
역시 Certificate는 집의 목록일거에요. 이 집들의 목록을 보면서 가중치를 합해가면 되겠죠? 그 가중치의 합을 아는것이 오래걸릴까요?
다항시간이 걸리게 됩니다.
만약 가중치를 합해서 K가 나온다면, YES!라고 대답하면 되는거고,
아니면 가만히 있으면 된다고 그랬죠?
다항시간에 Verify할 수 있으므로 NP임을 증명할 수 있고, NP-Complete문제가 될 수 있는 조건을 만족하게 됩니다.
그럼 지금, 우리는 TSP가 NP-Hard인거만 증명하면 TSP가 NP-Complete가 되는 상황이죠?
즉, 위에서 Q가 TSP가 되면 됩니다.
즉!!! TSP를 푸는 알고리즘으로 헤밀토니안 사이클 문제를 풀면, TSP는 NP-Complete인 헤밀토니안 사이클 문제를 푼 것이므로 NP-Hard가 됩니다. 1번에서 TSP가 NP임을 증명했으니 NP-Complete가 되겠네요.
헤밀토니안 사이클 문제의 인풋 -> Transformation Function -> TSP의 인풋
을 해볼까요?
참고로 헤밀토니안 사이클 문제의 인풋은 그냥 "무향 그래프"입니다. TSP의 인풋이 뭐였는지 기억나시나요?
"무향 완전 가중 그래프"였죠? (인풋이 하나 더 있습니다. Decision버전에서는 가중치의 합인 K가 있었죠?)
즉, 헤밀토니안 사이클 문제에서의 인풋은 완전 그래프가 아니어도 됩니다. == 모든 노드들간에 간선이 없어도 됩니다. 그냥 "무향 그래프"이기만 하면 됩니다.
이걸 Transformation Function을 통해서 TSP의 인풋으로 만들어볼게요.
무향 그래프 -> Transformation Function -> 무향 완전 가중 그래프, K
1. 모든 노드들간에 간선이 없다 -> 모든 노드들간에 간선이 있도록 만들자!
2. 간선에 가중치가 없다 -> 간선에 가중치를 주자!
이렇게 하면, TSP의 인풋인 무향 완전 가중 그래프가 만들어 질 것 같네요!
가중치는 주는데에는 조건이 있습니다.
1. 원래 있던 간선에는 가중치를 0을 준다.
2. 추가되는 간선에는 가중치를 1을 준다.
마지막으로, 우리 TSP의 인풋이 뭐라고 그랬죠? 지금 TSP의 Decision버전을 가지고 NP-Complete임을 증명한다고 그랬죠?
그러면 여기서 K가 필요합니다.
도대체 얼마의 가중치의 합을 가지도록 할것인지 정해야겠죠?
이 K를 0으로 set해줍니다.
자, 우리는 지금
헤밀토니안 사이클 문제의 인풋(무향그래프)을 TSP의 인풋(무향 완전 가중 그래프, K)으로 바꿨고,
이제 TSP를 푼 결과가 헤밀토니안 사이클 문제의 모든 인스턴스에 대해서 참인 결과를 낼 수 있다면,
우리는 TSP를 푸는 알고리즘으로 헤밀토니안 사이클 문제를 푼것이므로 TSP가 NP-Hard가 되겠네요.
TSP를 풀어봅시다.
Q : (무향 완전 가중 그래프를 주며) 이 그래프에서 모든 노드들을 한번씩만 방문하고, 그 가중치의 합이 0인게 있어? (Decision ver.) (위에서 K는 0으로 set해줬기때문)
(== 이 그래프에서 K=0인 헤밀토니안 사이클이 있어?)
만약!!!!!!!!!
K가 0인 헤밀토니안 사이클이 있다고 가정해봅시다.
우리 아까 추가된 간선에는 가중치를 1로 줬었죠?
만약!!!! K가 0인 헤밀토니안 사이클이!!!있다면!!!!!!
이 추가된 간선을 한번이라도 지날 수 있을까요?
이 추가된 간선은 지나지 않았다!!!!라는 것이 되겠죠.
또 주목해야할 점이 있습니다.
즉!!!!!! TSP의 인풋으로 바꾸기 전의, 헤밀토니안 사이클 문제의 인풋이었죠?
아니 우리 지금 K가 0이려면, 추가된 간선은 한번도 안지나야되는데,
지금 우리가 헤밀토니안 사이클의 인풋을 TSP의 인풋으로 바꿨지만,
결국!!!!!!!!결국엔 추가된 간선을 한번도 사용하지 않았으므로 헤밀토니안 사이클의 인풋을 그대로 쓴 것이죠.
(가중치는 있지만)
그러니까!!! TSP가 YES이면, 당연하게 헤밀토니안 사이클 문제도 YES가 되는거죠.
우리는 지금 TSP를 풀었지만, 추가된 간선을 건드린게 없으니 헤밀토니안 사이클을 자연스럽게 푼것이죠.
만약 TSP가 NO라면?
TSP가 NO라는 소리는, K가 0인 헤밀토니안 사이클이 없다
== 가중치의 합이 0이 아니다 == 추가된 간선. 즉, weight가 1인 간선을 지났다.
== 원래 헤밀토니안 사이클 문제의 인풋에는 없던 간선 == 헤밀토니안 사이클 문제에서도 NO.
그렇습니다.. TSP가 NO라면, 헤밀토니안 사이클 인풋에서는 존재하지도 않던 간선을 지난 것과 마찬가지이므로 헤밀토니안 사이클 문제에 대한 대답도 NO가 되게 됩니다.
결국, 우리는 TSP를 푸는 알고리즘으로 헤밀토니안 사이클 문제를 푼 것이죠?
즉!! “TSP는 NP-Hard”라고 할 수 있겠네요.
1과 2를 통해 최종 결론을 내자면,
TSP는 NP에 속하며 동시에 NP-Hard이므로 NP-Complete이다.
- Prime number problem
NP-hard
-
at least as hard as an NP-complete set.
-
if a polynomial time algorithm exists for any NP -hard problem,
you can easily solve the NP-complete probl em in polynomial time, i.e., P = NP. -
Every NP-complete problem is in NP-hard,
and the optimization problem corresponding to any NP-complete problem is in NP-hard. -
How to handle NP-hard problem
• Use a backtracking algorithm or branch-and-bound algorithm, which checks all cases but excludes the parts that are needed
• Restricting the input to a planar graph rather than a regular graph, and to a tree rather than dealing with a planar graph
• Use an approximation algorithm to get approximate solution clos e enough to the optimal solution although there is no guarantee t o get an optimal one
6-1. Backtracking
Backtracking
-
useful technique for problems something like some puzzles/games (examples: 8-queen problem, crosswords, Sudoku, ... ) or NP-hard problems because it avoids much unnecessary subsets in the solution space
-
useful because they are efficient for many large instances, not because they are efficient for all large instances
• always gets an optimal solution -
Some problems require brute force approach (Need to explore all possible ways)
-
Then, how to solve such problems in an efficient manner
=> Exclude some ways which are not needed
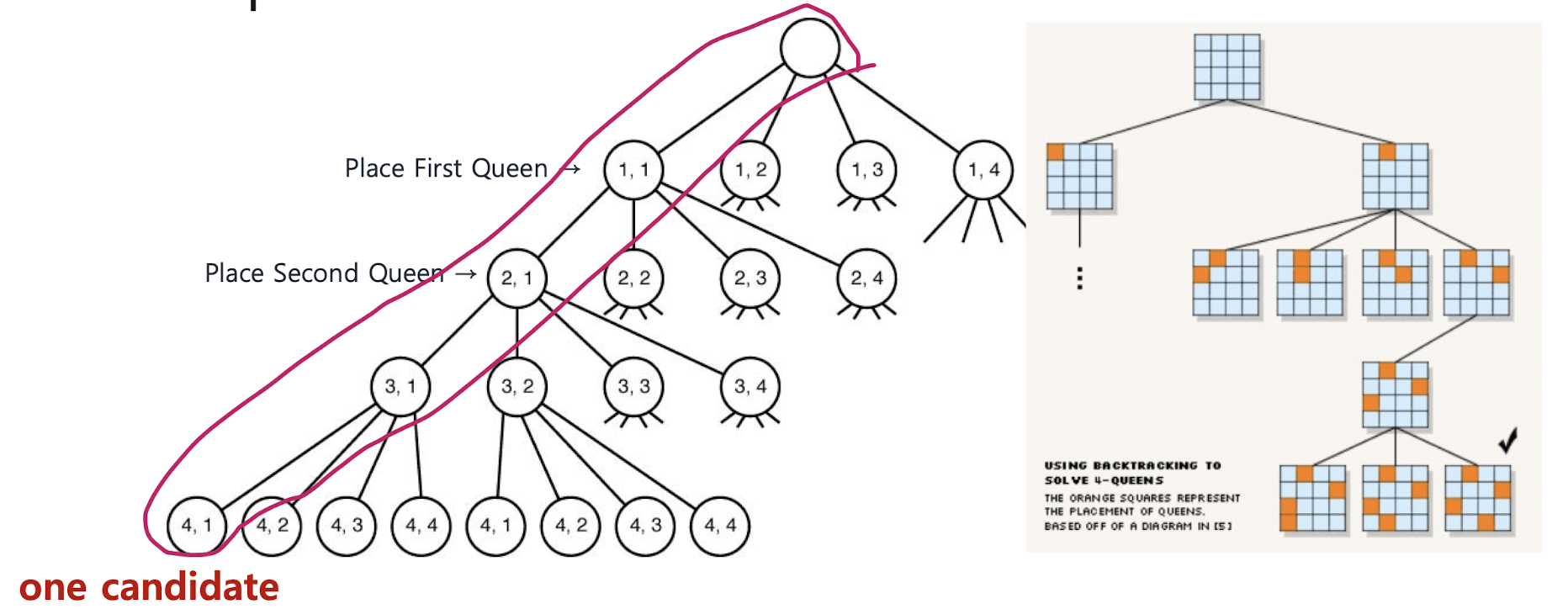
< State space tree >
- Record all the positions (row, column) during the intermediate steps
- Use depth first search from the root to traverse the tree
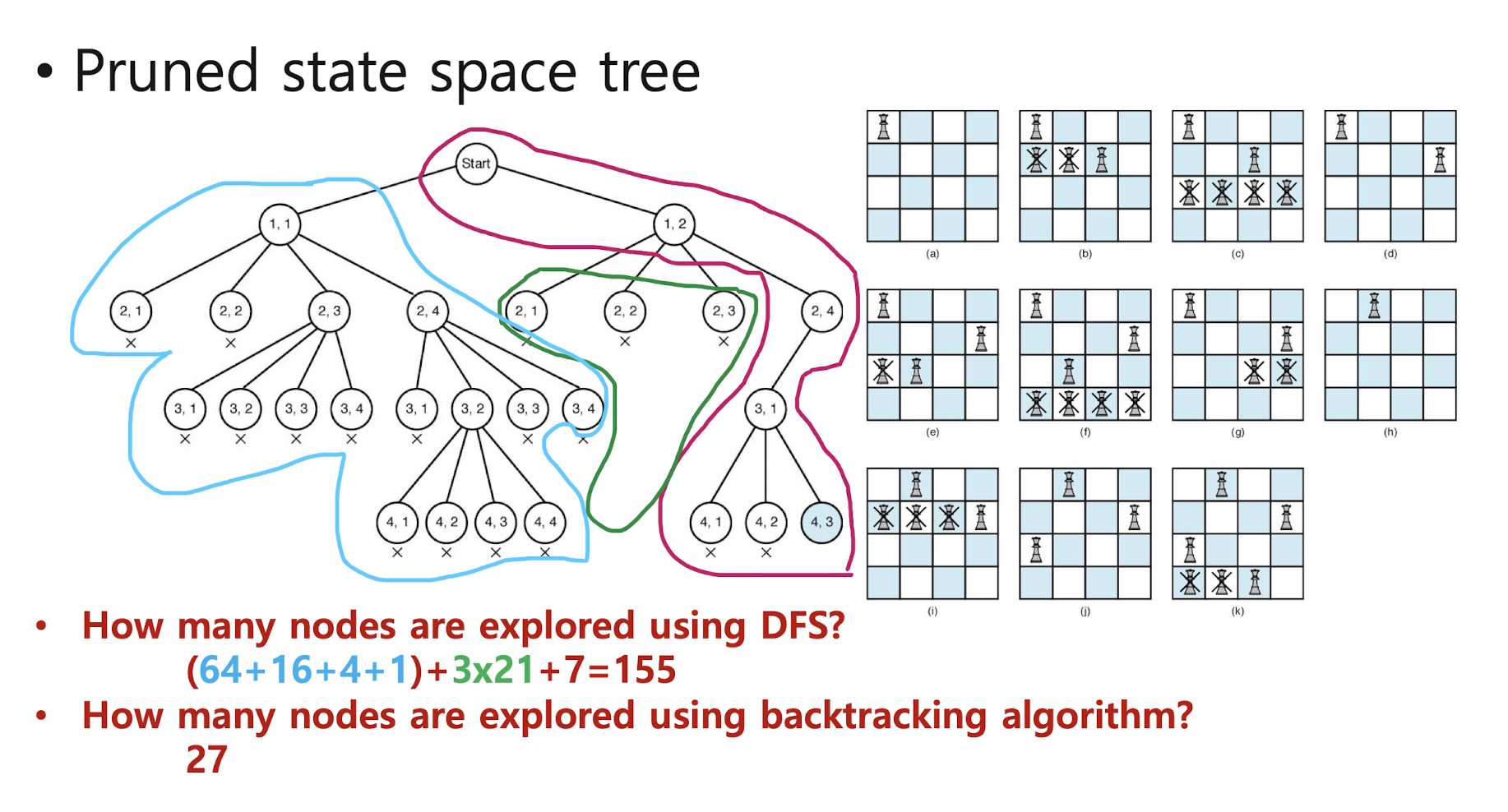
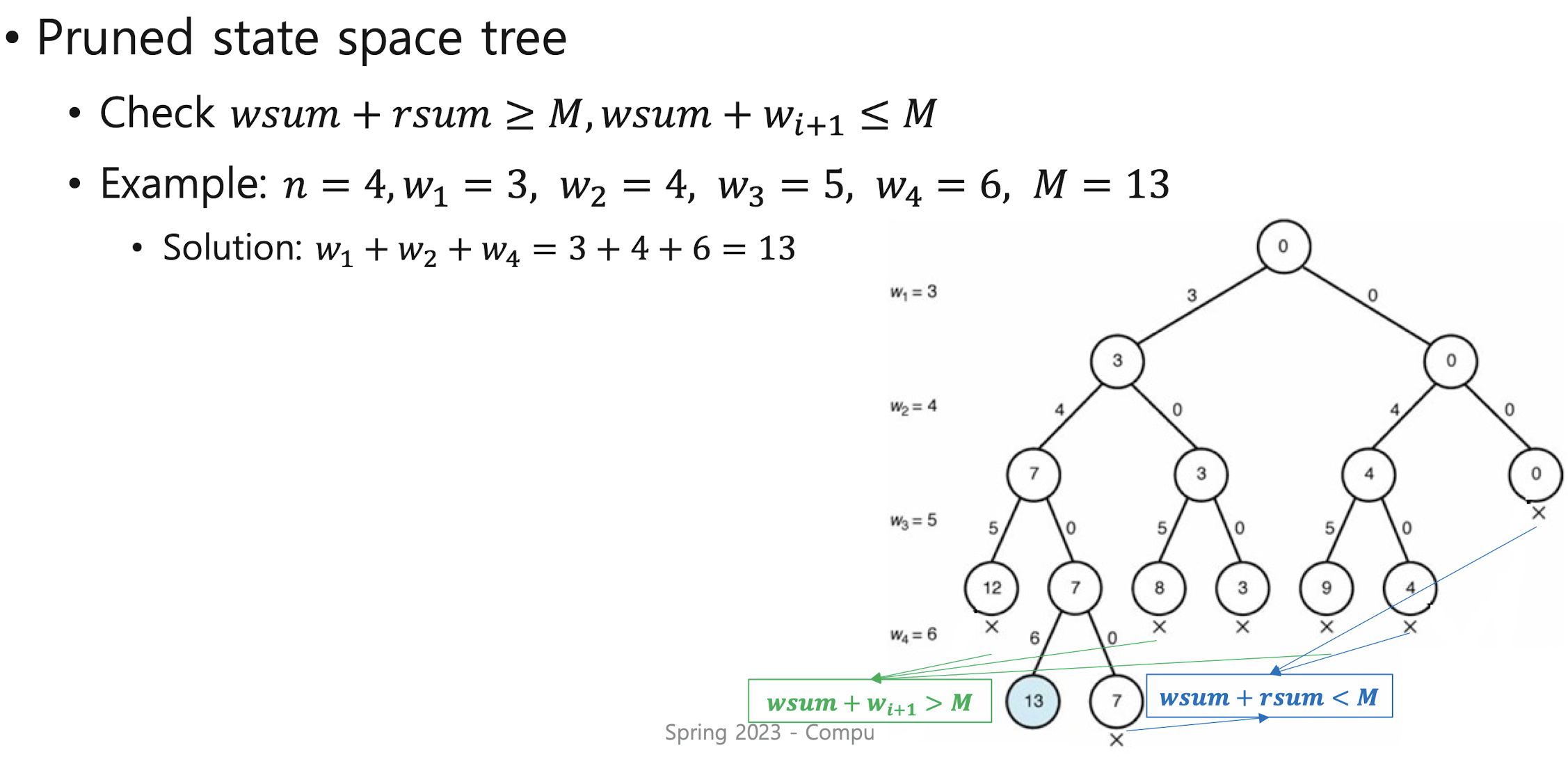
< Pruned state space tree >
- Do DFS on the state space tree but if the node can no longer produce a solution,
its subtree is not expanded and it goes back to the parent node of that node
and starts again from the next child node of that par ent node - This is called pruning
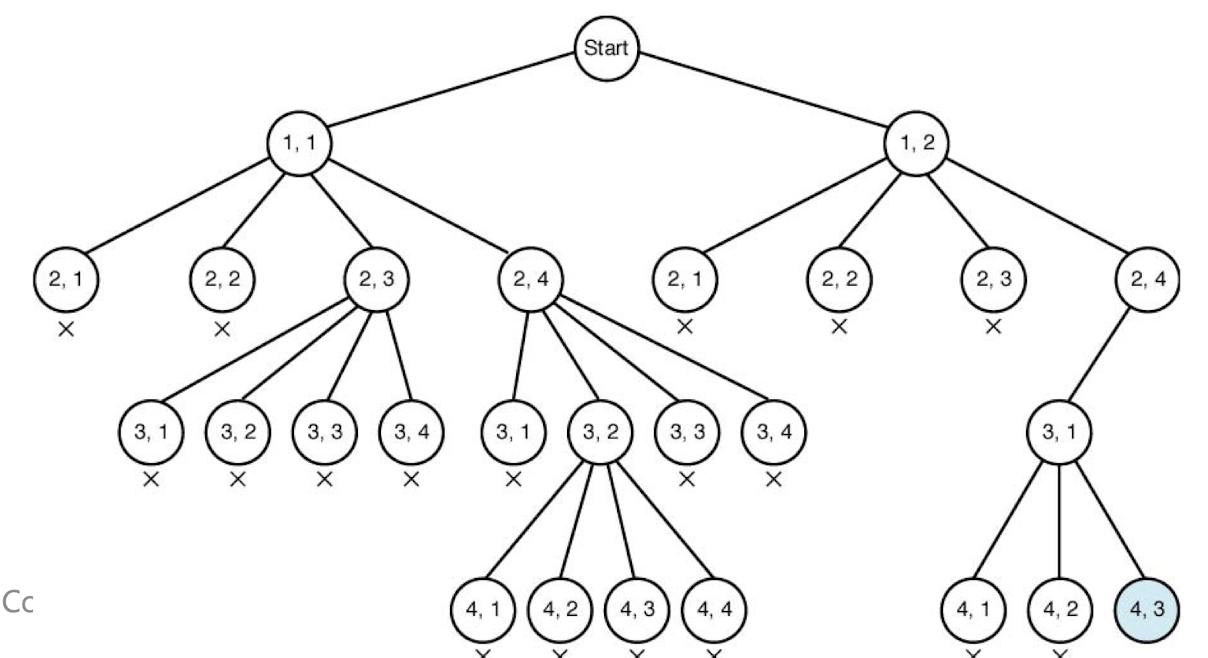
===>>>
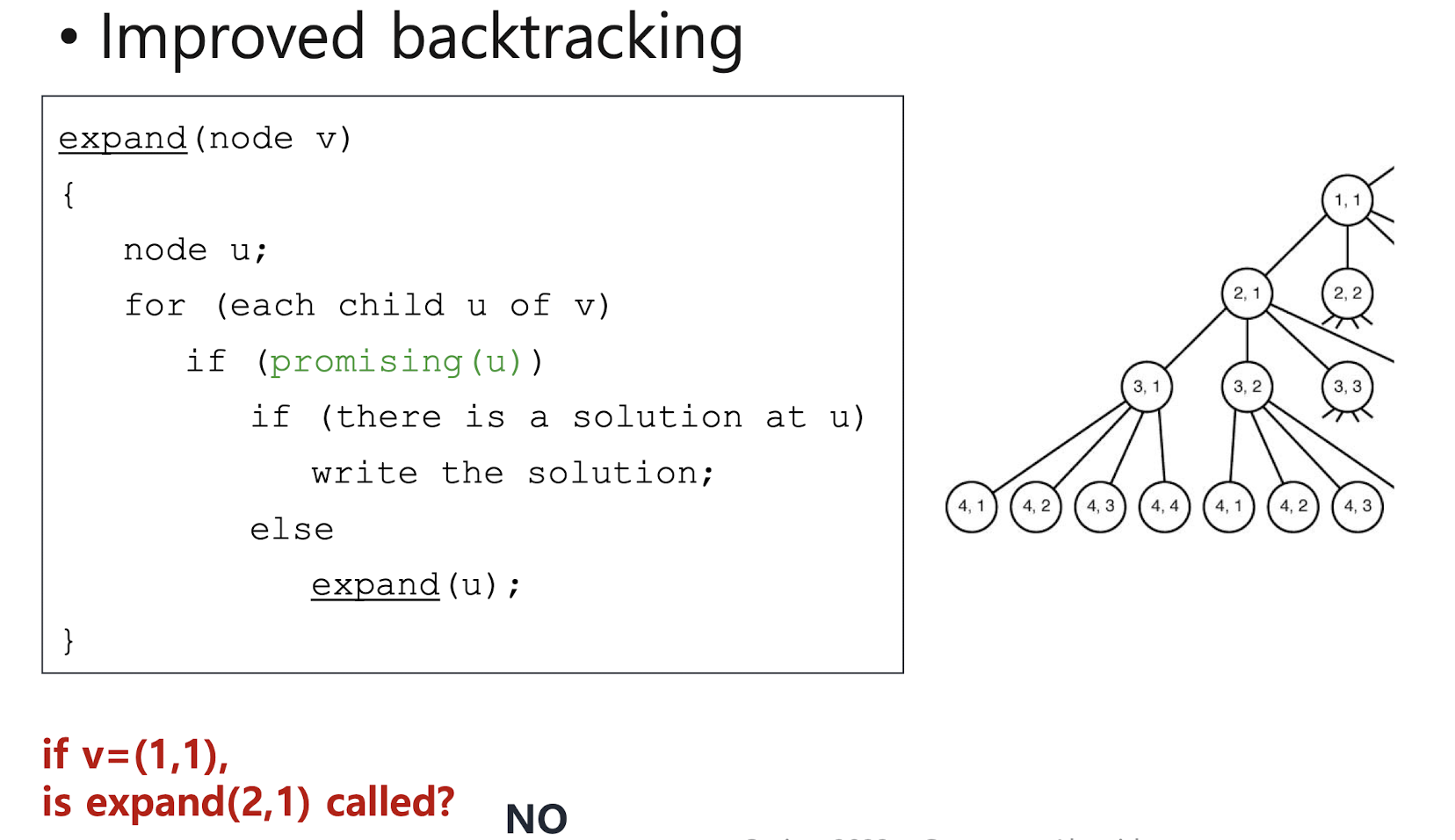
- Pruning: if a node is non-promising, we "go back (backtrack)" to the node's parent
- Backtracking algorithms: For non-promising nodes, stop se arching. Only for promising nodes, search their child nodes
4-queens problem


N-queens problem


< n-queen problem analysis - How to get of nodes to be visited >
n-Queens문제의 성능을 어떻게 분석할까?
상태공간트리의 전체 노드의 상한(upper bound) 개수를 구하거나 유망한 노드의 상한 개수를 구해볼 수 있다. 하지만 이는 '상한'일 뿐, 정확한 복잡도를 알 수 없다.
결국에는 이미 구축이 완료된 상태공간트리의 노드 개수를 실제로 세어보는 수 밖에 없다.
하지만 이 방법은 진정한 분석 방법이라고 할 수 없다. 분석은 알고리즘을 실제로 수행하지 않고 이루어져야하기 때문이다.
따라서 성능을 계산할 수 없으므로, '추정'해볼 수 있는데, 이처럼 알고리즘의 성능을 추정할 때 사용하는 알고리즘을 'Monte Carlo 기법'이라고 한다.
Monte Carlo Estimation
Monte Carlo 알고리즘은 어떤 입력이 주어졌을 때 그에 따라 생성되는 상태공간트리의 전형적인 경로를 무작위로 생성하고, 그 경로상에 있는 노드의 수를 센다.
이 과정을 여러 번 반복하여 나오는 결과의 평균치가 곧 추정치가 된다.
이처럼 Monte Carlo 알고리즘은 무작위 표본의 추정치를 사용하여 무작위 변수의 기대치를 측정하는 확률적 알고리즘이다. 이 알고리즘을 사용하기 위해 만족해야할 조건 2가지는 아래와 같다.
<Monte Carlo 알고리즘을 사용하기위해 만족해야할 조건 2가지>
① 상태공간트리에서 같은 수준(level)에 있는 모든 노드에서는 같은 유망함수를 사용해야 한다.
② 상태공간트리에서 같은 수준에 있는 모든 노드들은 같은 수의 자식노드들을 가지고 있어야 한다.
<Monte Carlo 알고리즘을 사용한 backtracking 알고리즘 수행시간 추정 방법>
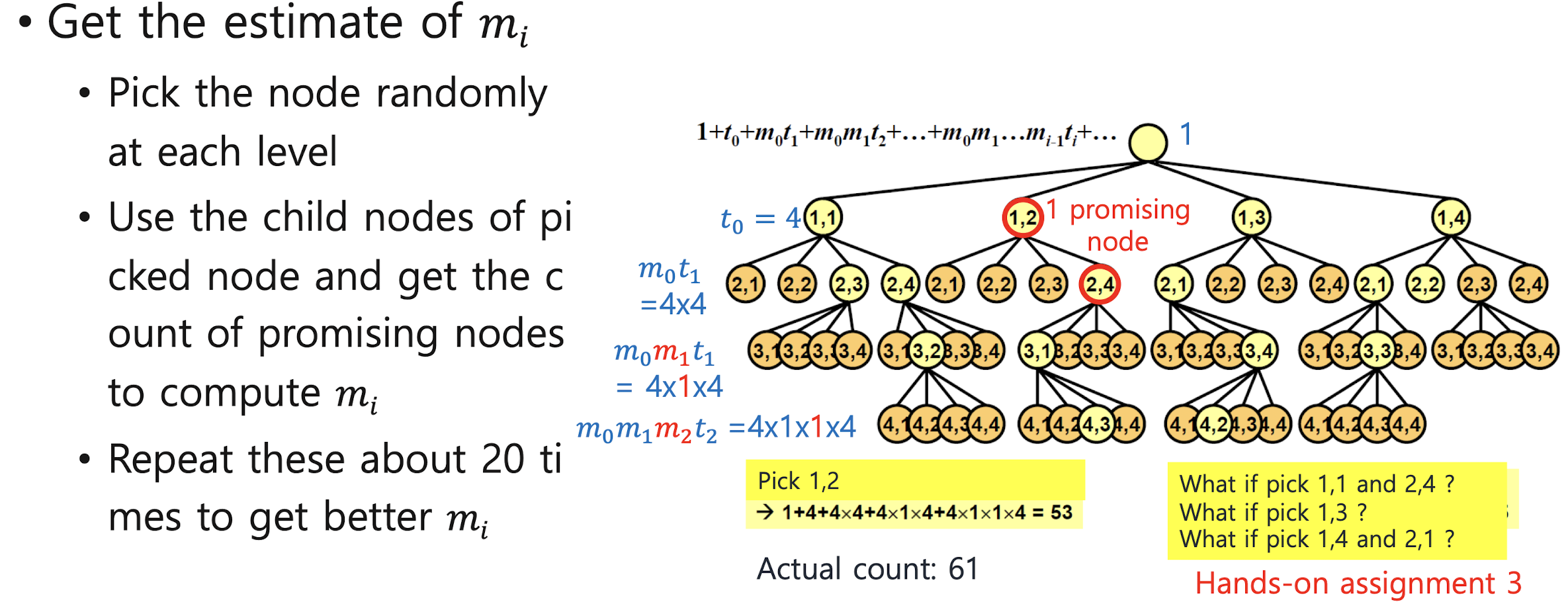
① 상태공간트리의 각 수준 i 에 있는 노드의 유망한 자식 노드의 개수를 mi라고 한다.
수준 i의 유망한 자식 노드들 중 유망한 노드 하나를 무작위로 정하고,
그 노드의 유망한 자식 노드의 개수를 다시 mi+1이라고 한다.
이를 수준 0 에서부터 더 이상 유망한 자식노드가 없을 때까지 이 과정을 반복한다.
② 위 과정을 반복하면서 각 수준 i 에 대해 다양한 값의 mi가 나오는데,이 값들의 평균값을 mi에 다시 저장한다.
③ ti에 수준 i에 있는 한 노드의 자식 노드의 총 개수를 저장한다.
④ 노드의 총 개수의 추정치 = 1 + t0 + m0t1 + m0m1t2 + ··· + m0m1···mi-1ti + ···
(더 이상 유망한 자식노드가 없거나 트리의 끝에 도달할 때 까지)
표본, mi, ti에 대한 이해를 돕기 위해 아래 그림을 첨부하였다. 아래 그림의 상태공간트리의 노드는 모두 4개의 자식 노드를 갖고있으며 상태공간트리의 일부가 생략되어있다.



Subset sum problem
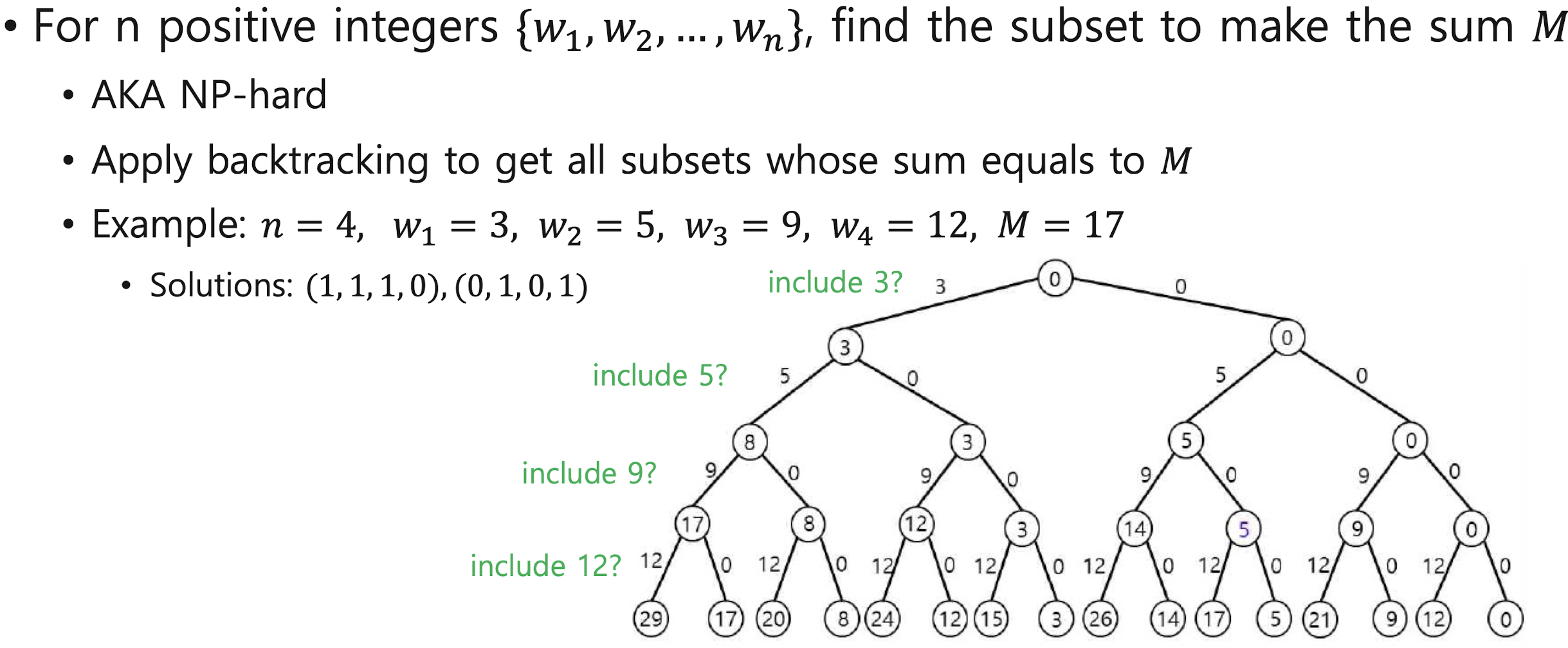

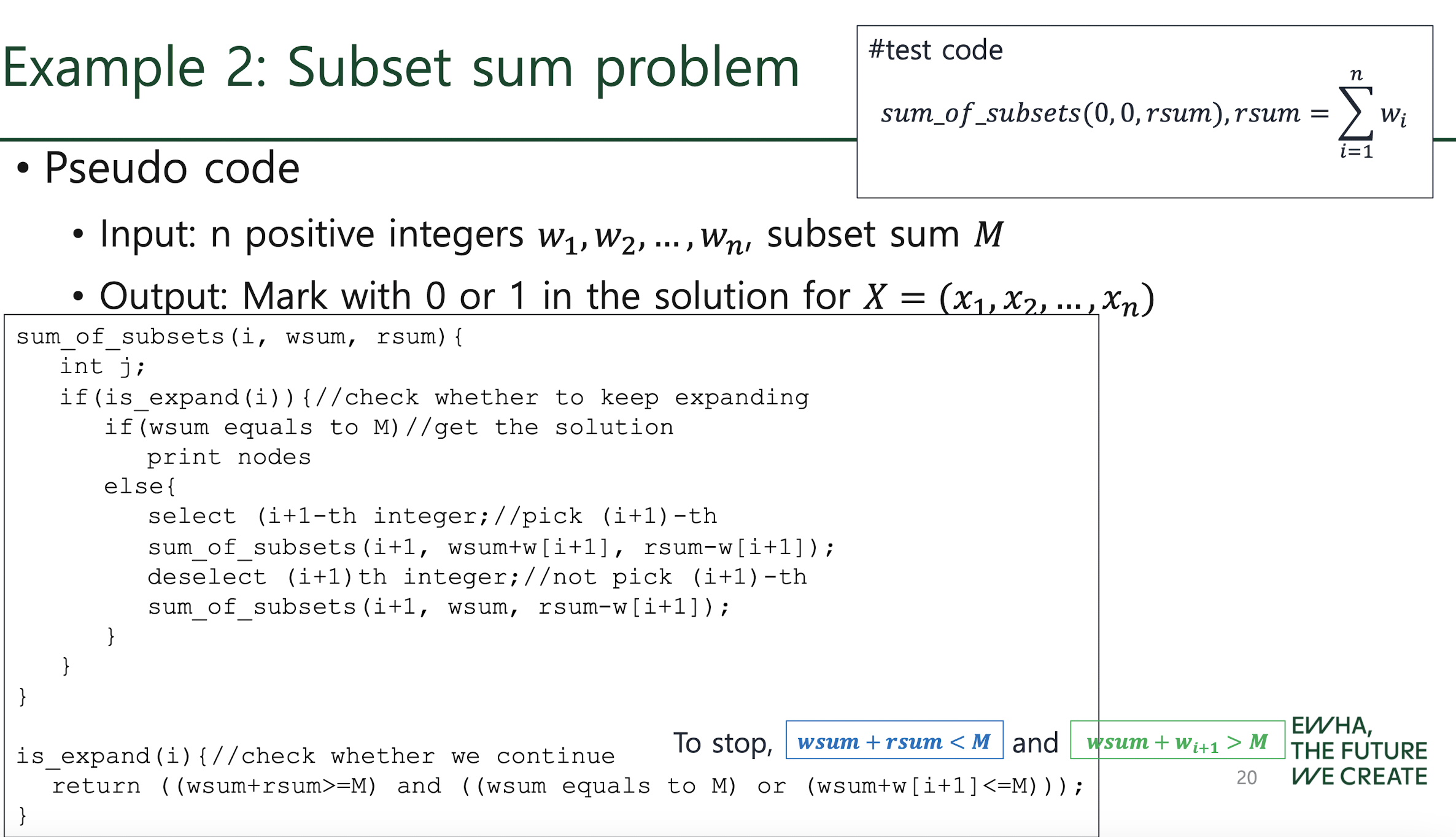
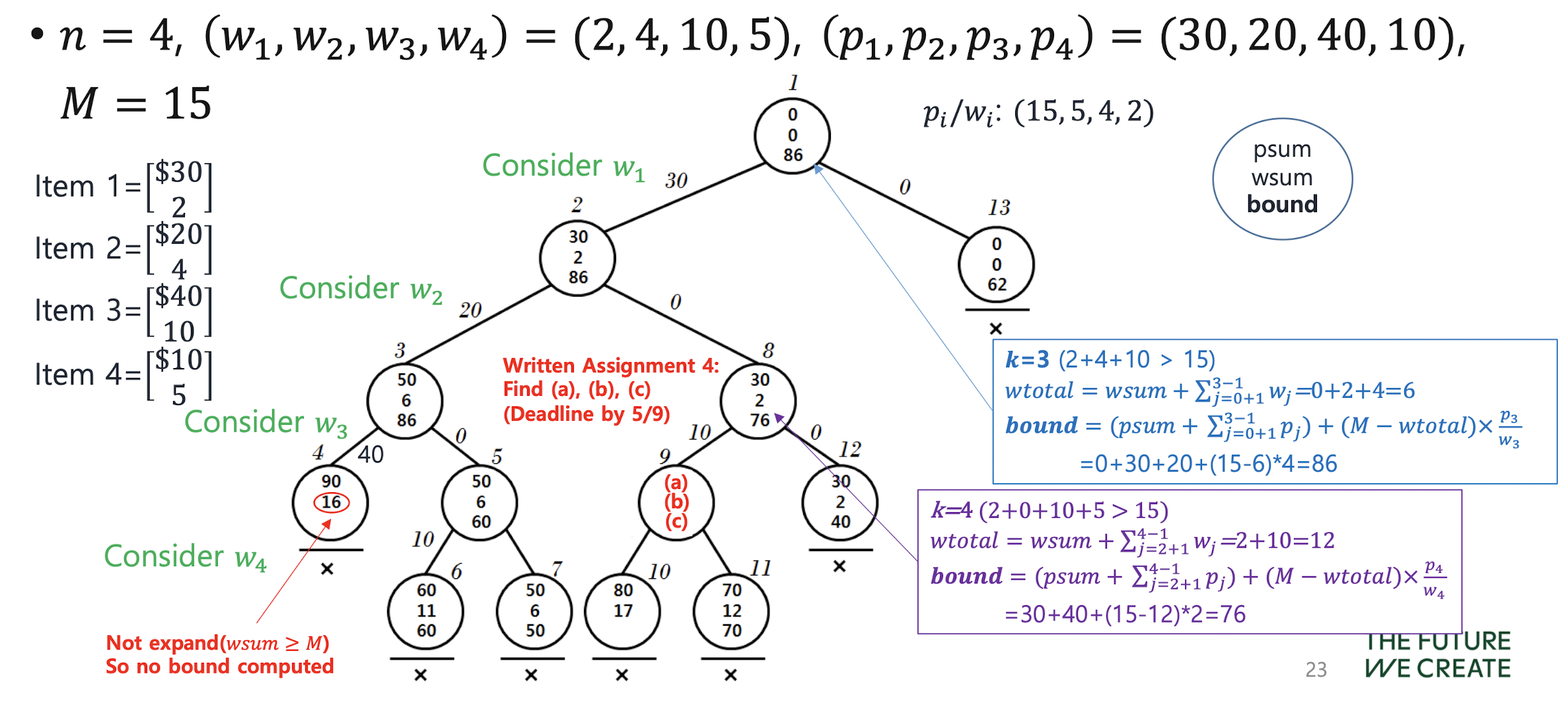
0-1 knapsack problem


6-2. branch-and-bound
Branch-and-bound (B&B)


FIFO (Breadth-first Search) B&B
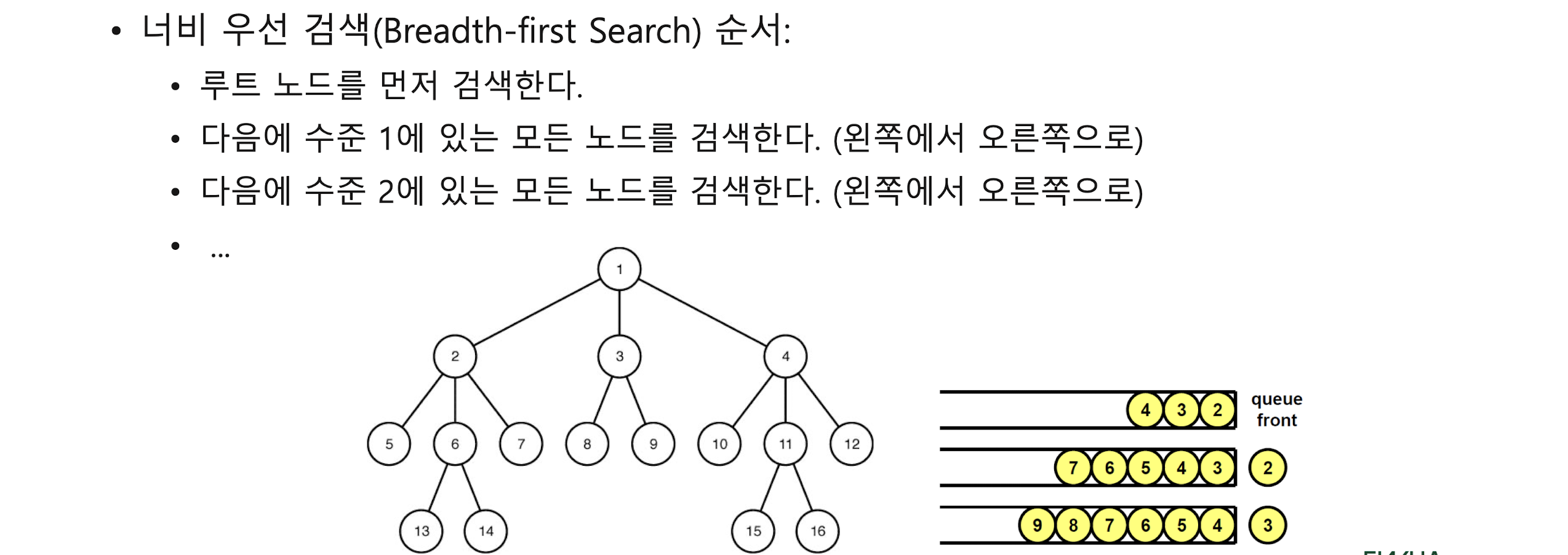

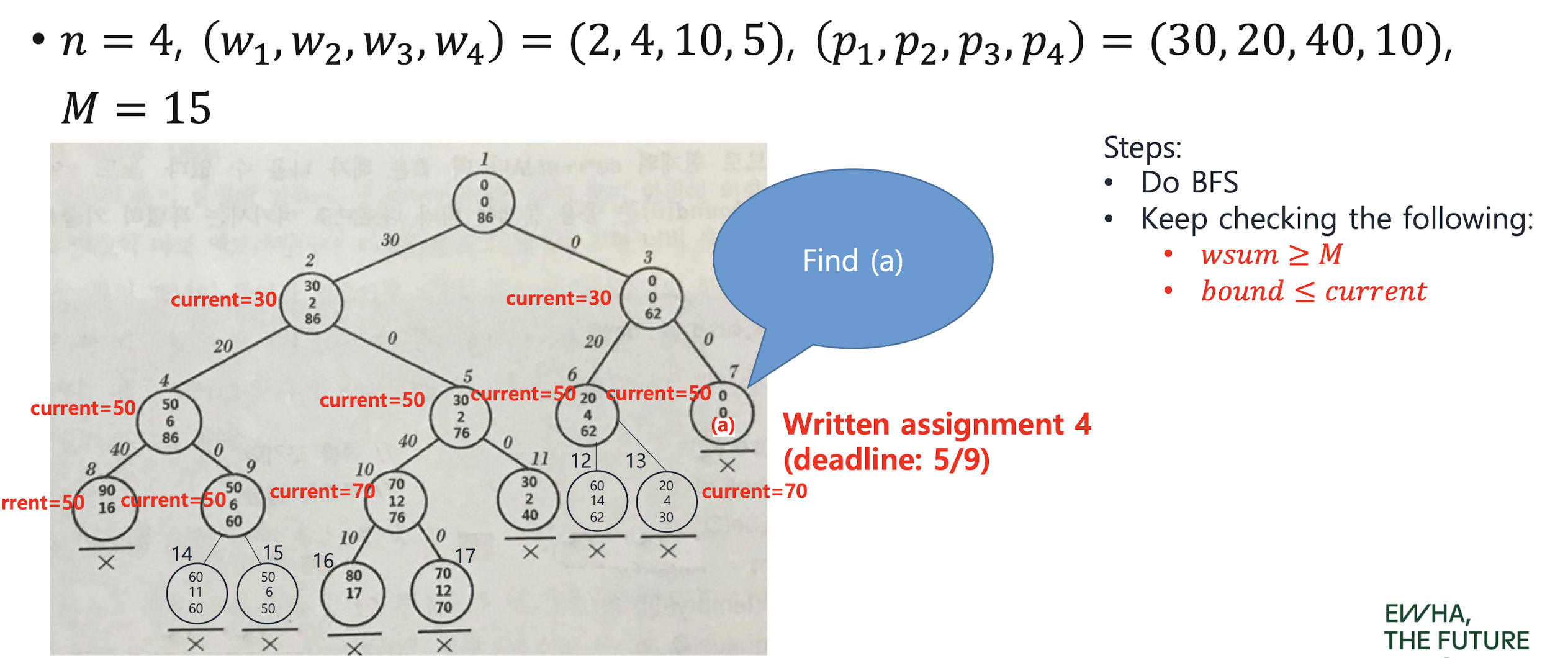
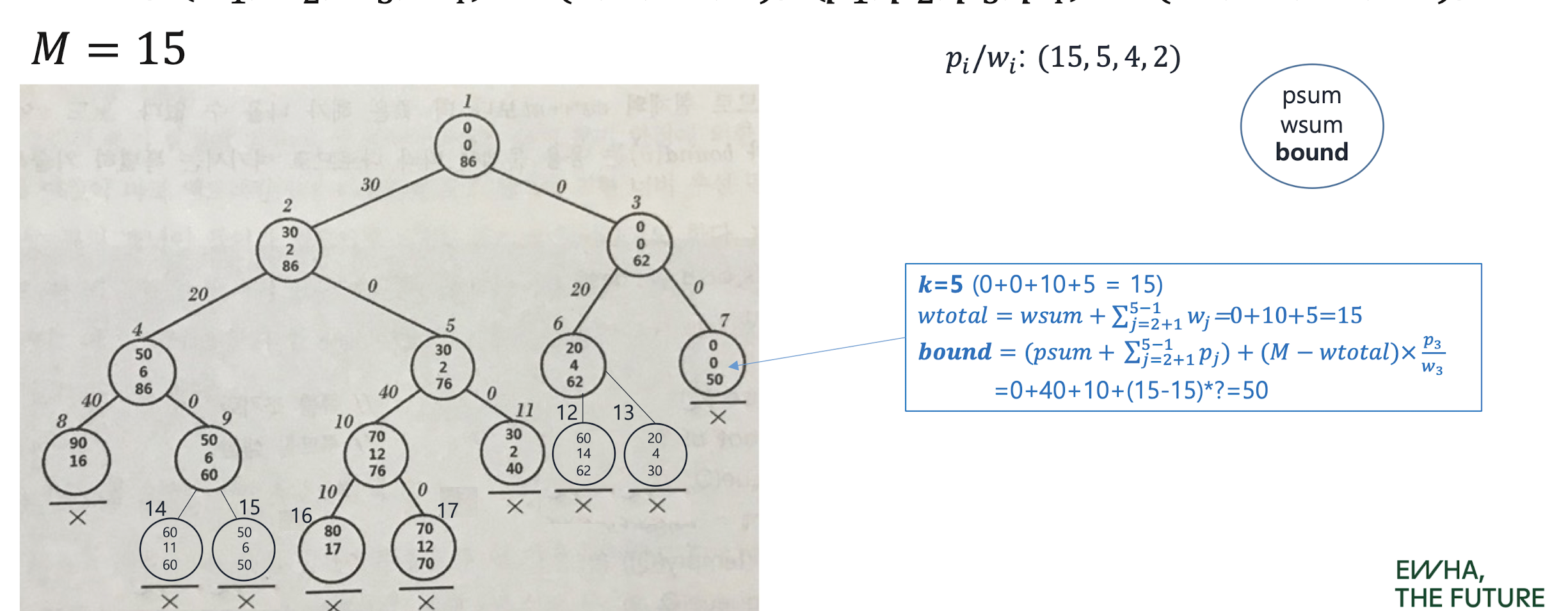
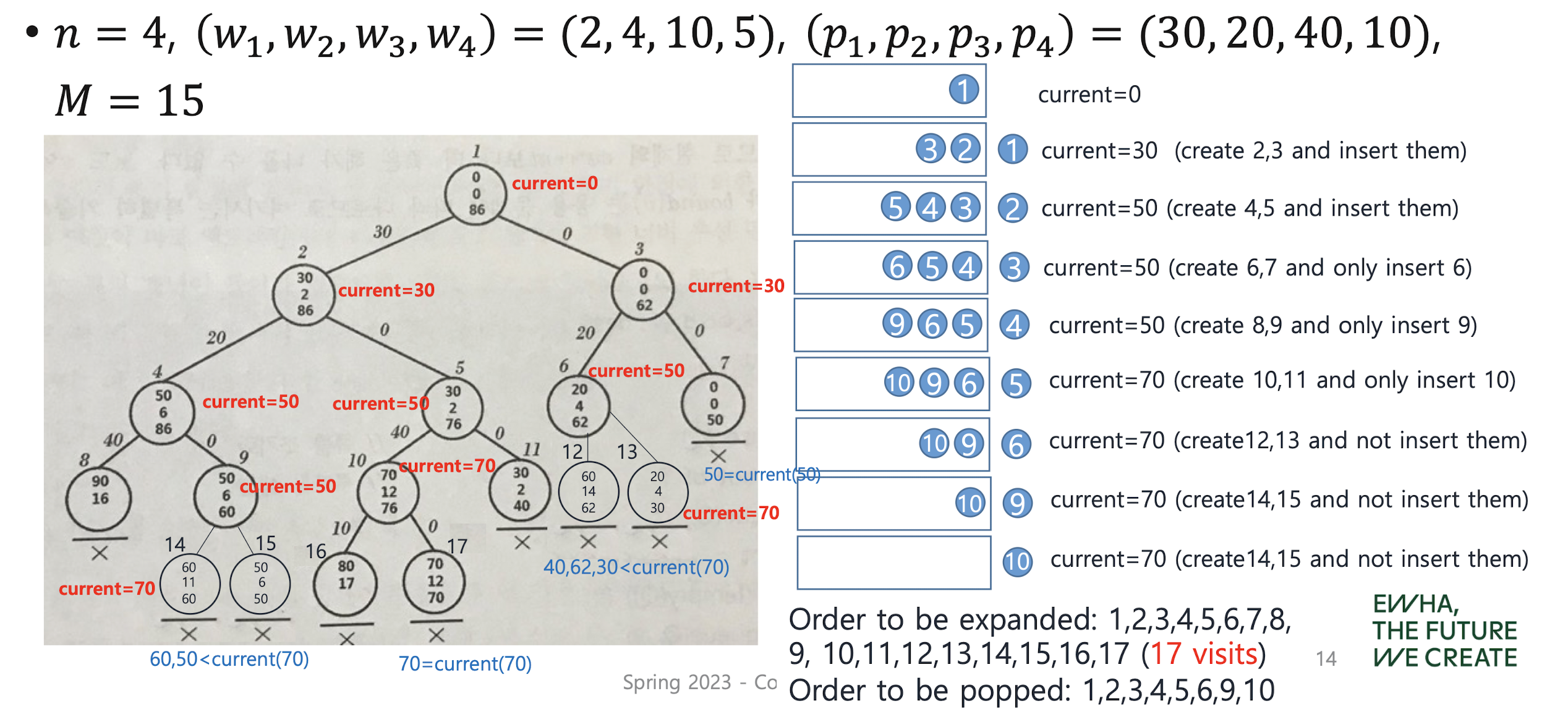
Revisit 0-1 knapsack problem with FIFO B&B
그냥 큐 사용
LC (Best-First Search) B&B
우선순위 큐 사용
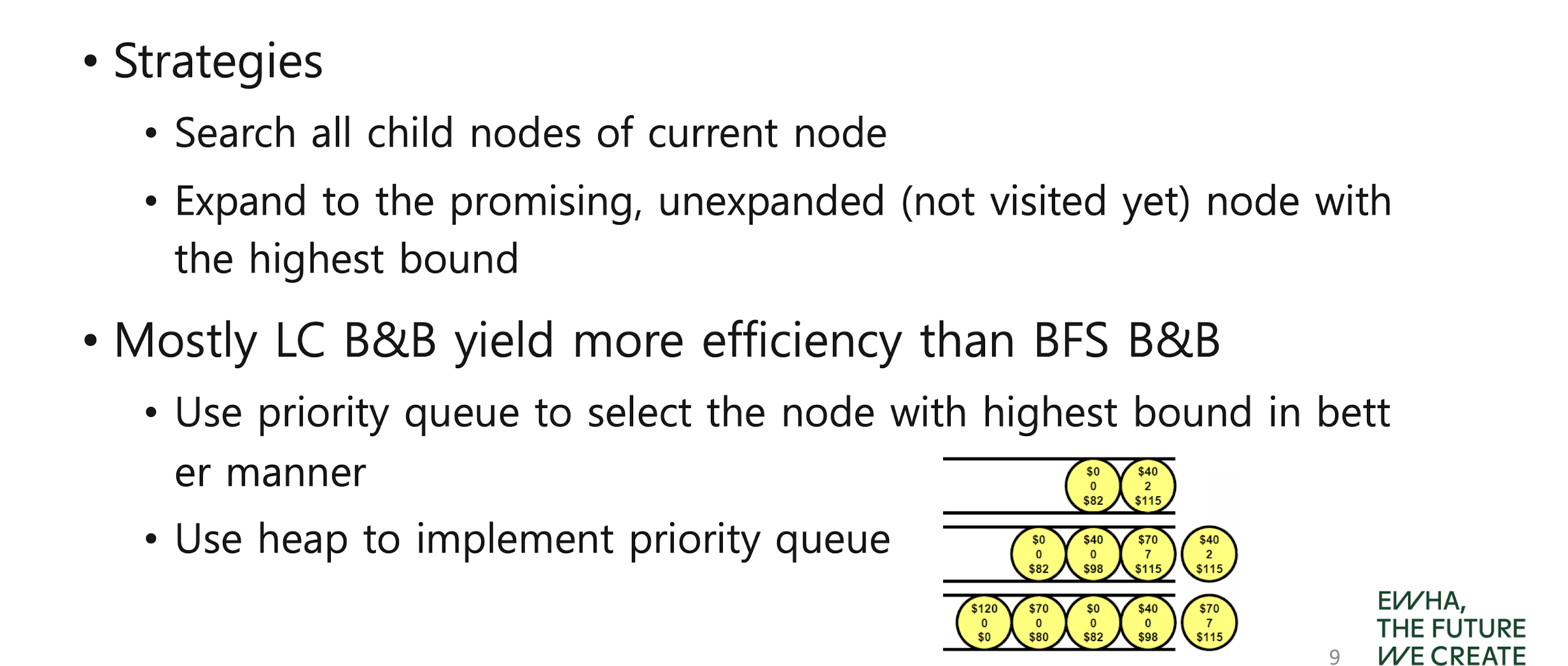

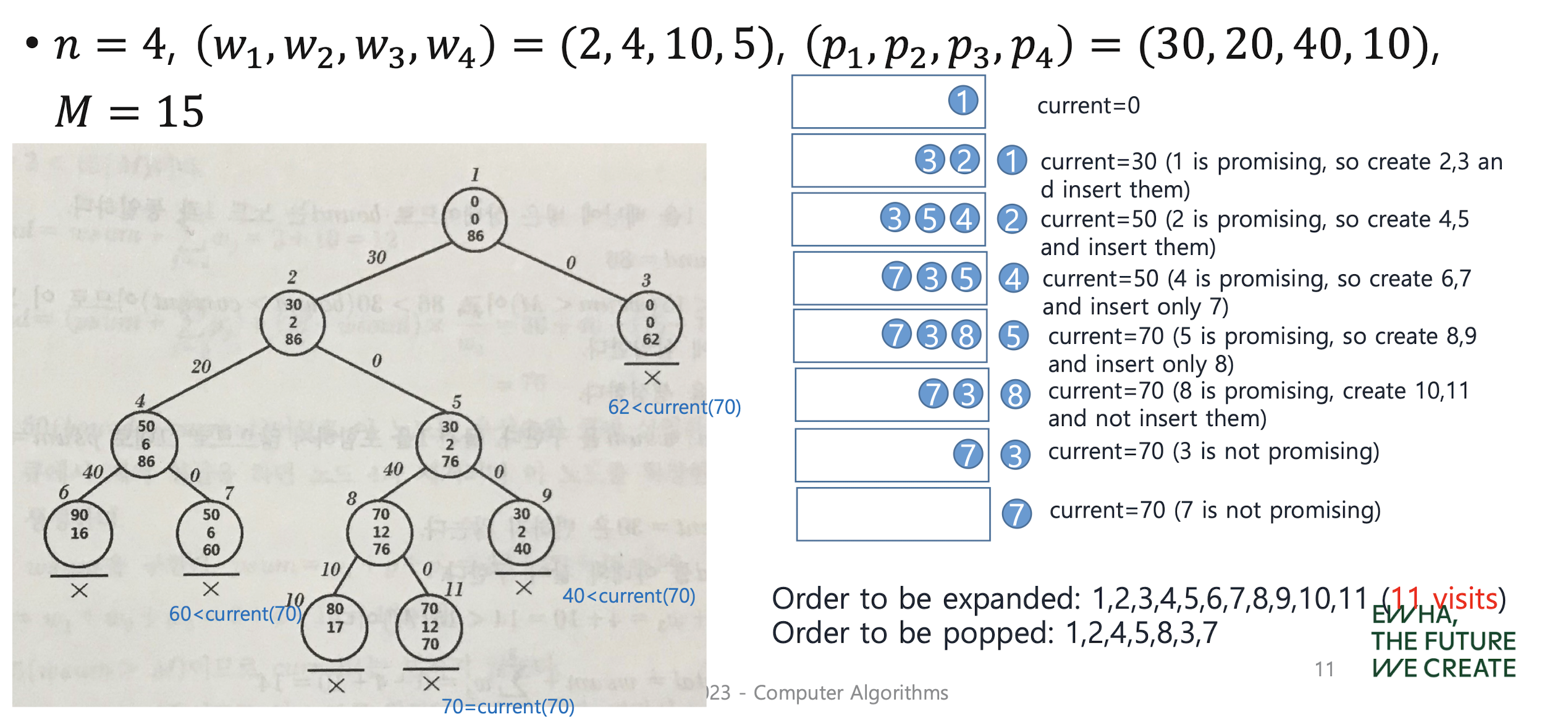 Count of expanded nodes: 11 (vs 17 for FIFO B&B)
Count of expanded nodes: 11 (vs 17 for FIFO B&B)
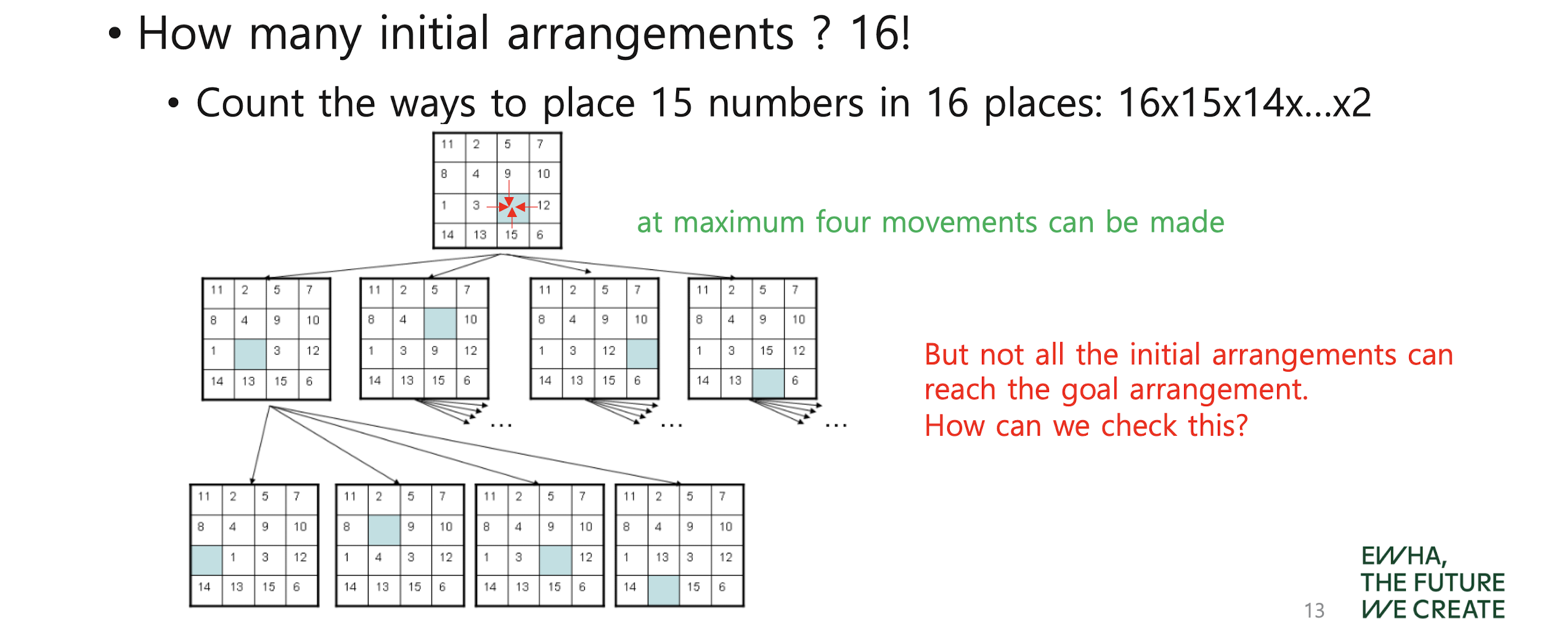
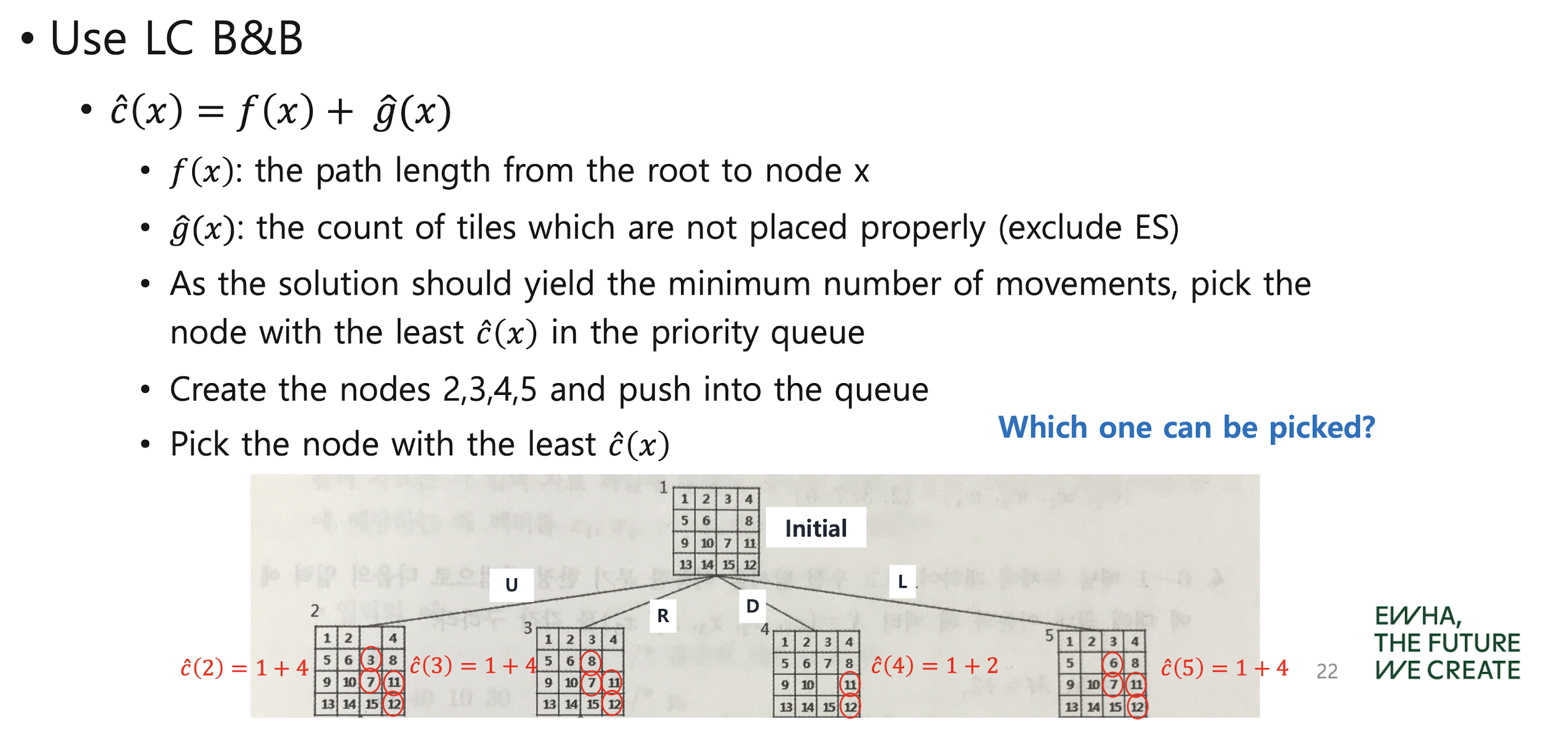
The 15 puzzle problem with LC B&B


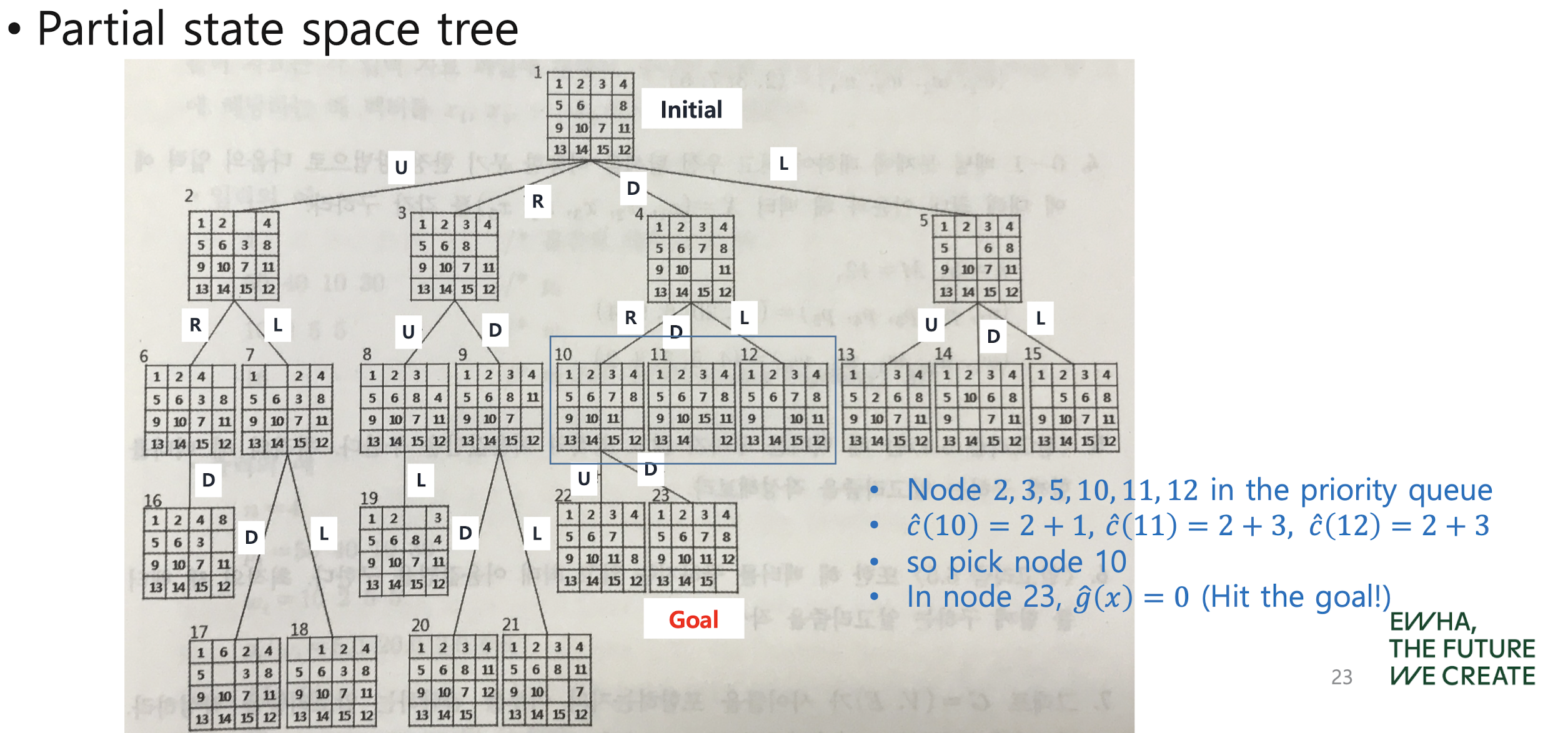
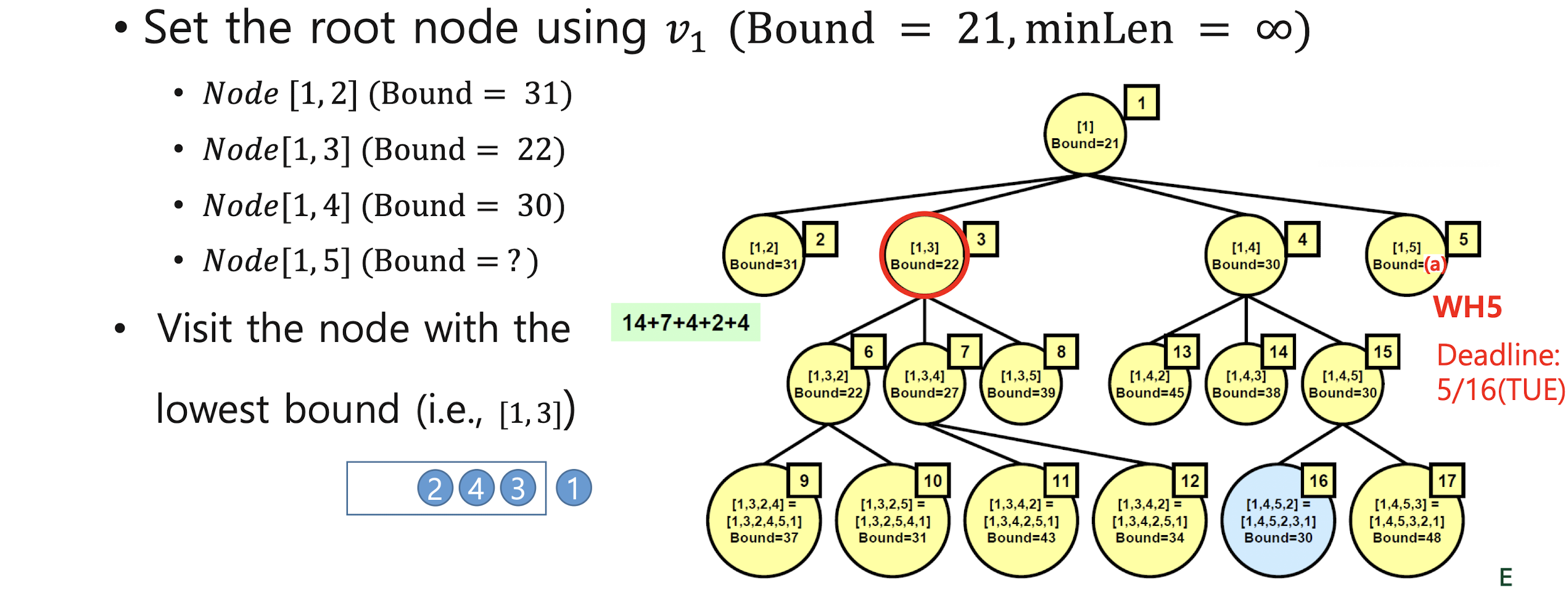
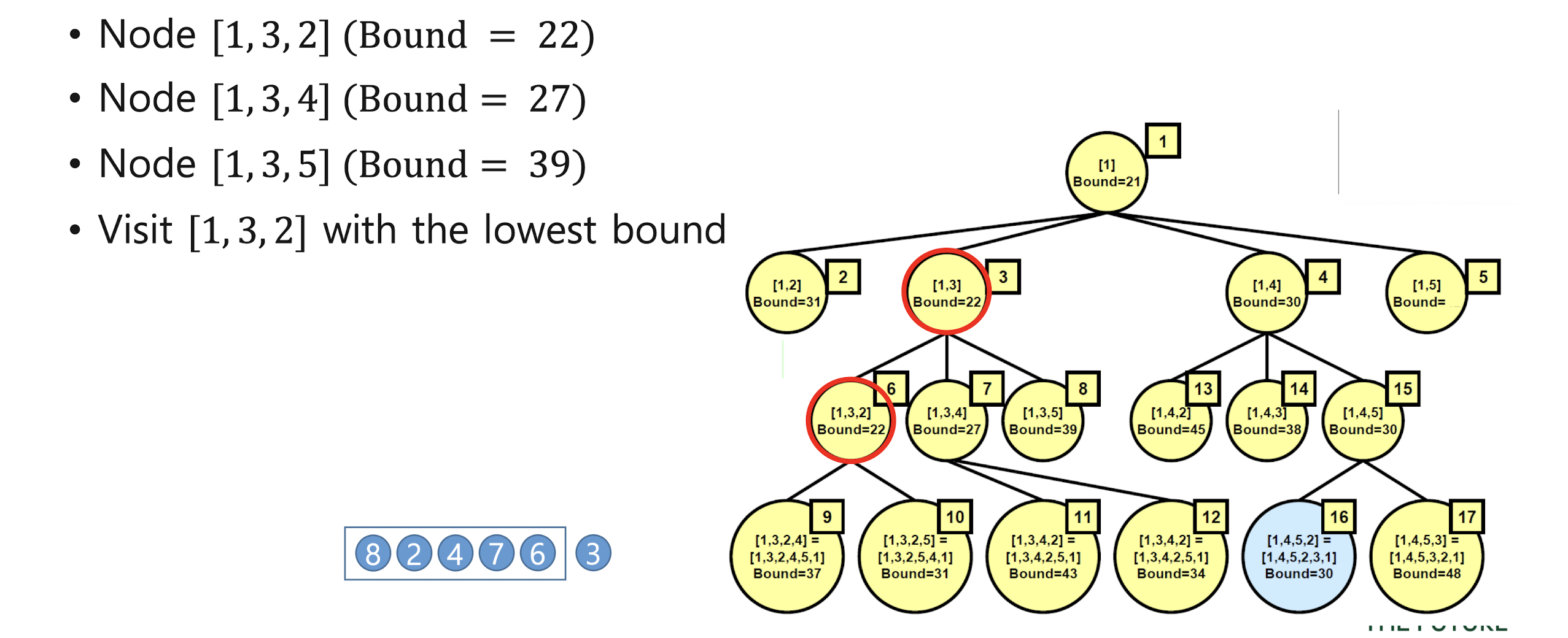
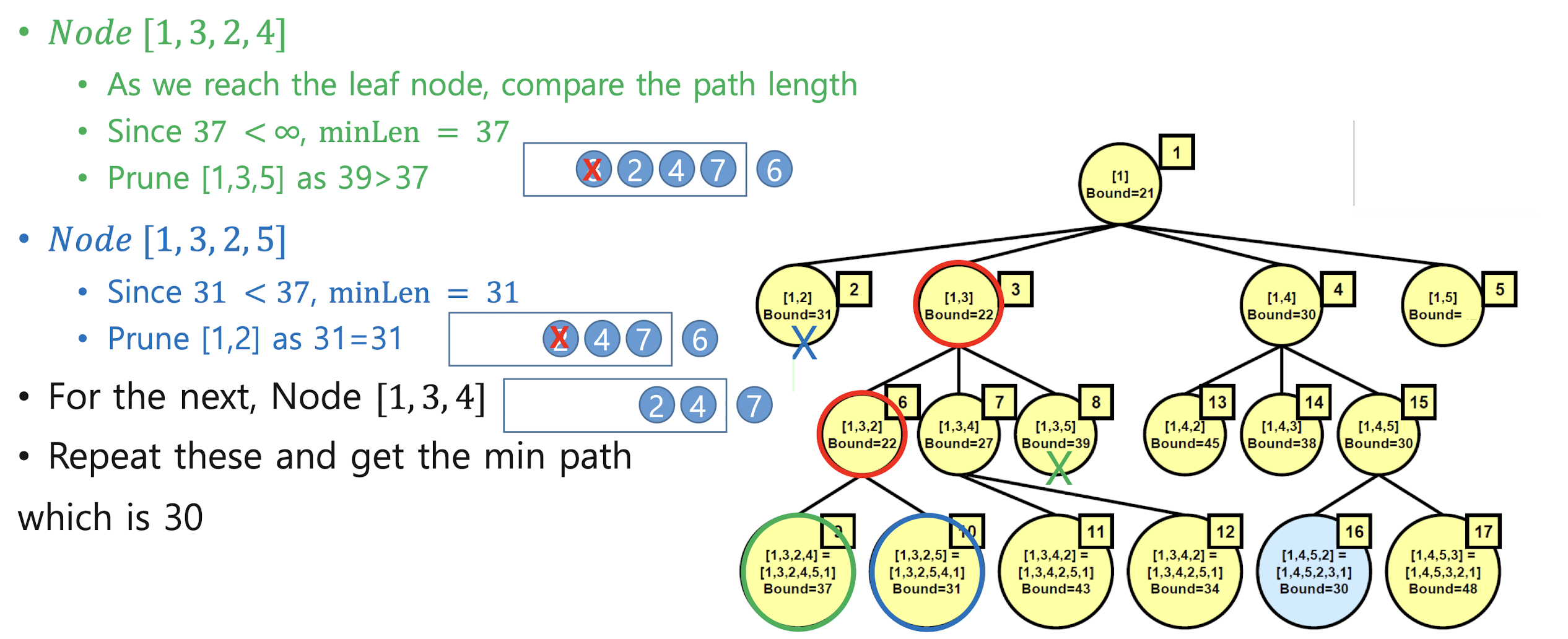
Traveling Salesman Problem with LC B&B






7. Sorting and searching
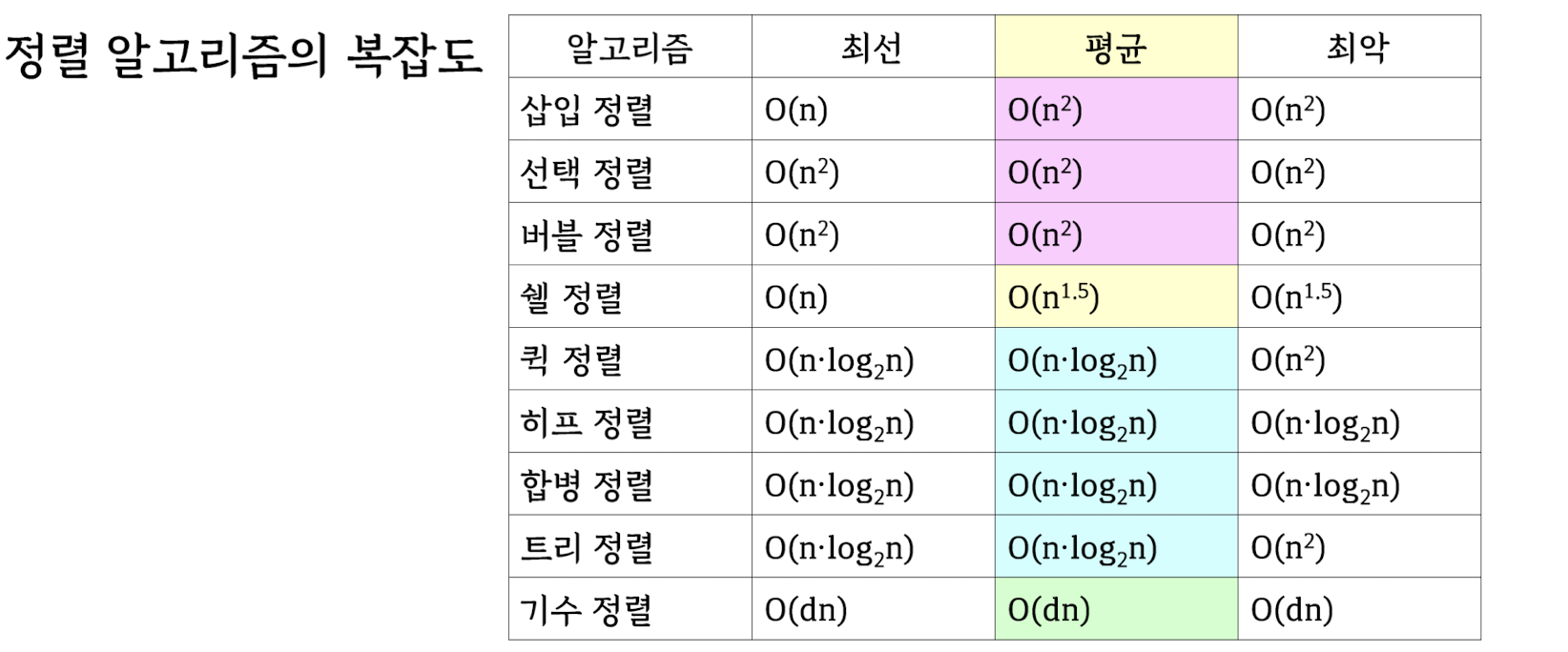
Sorting algorithms


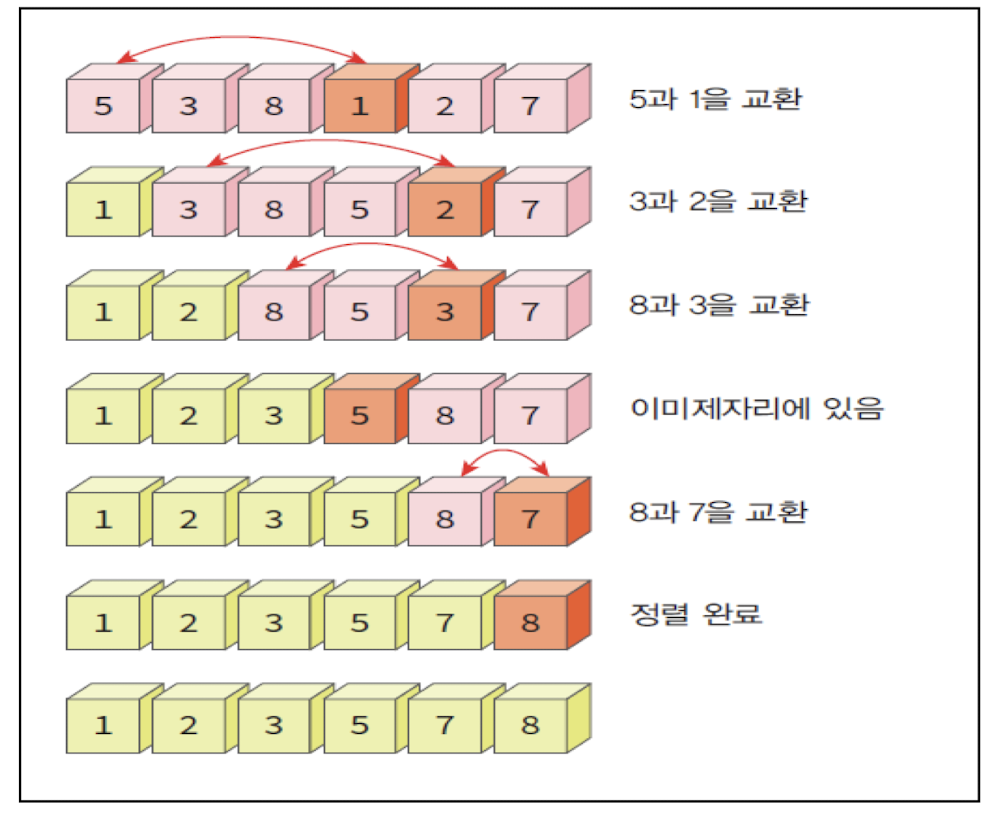
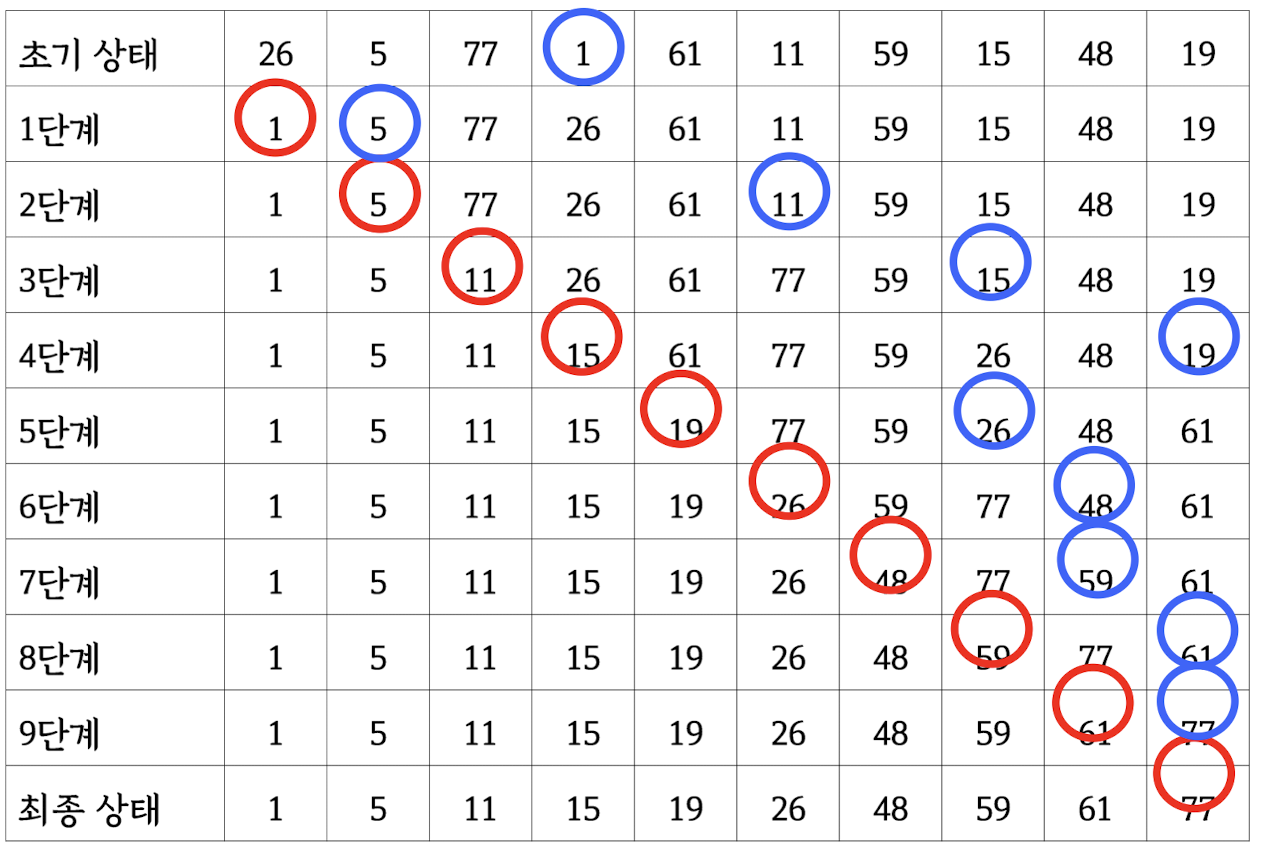
Selection sort


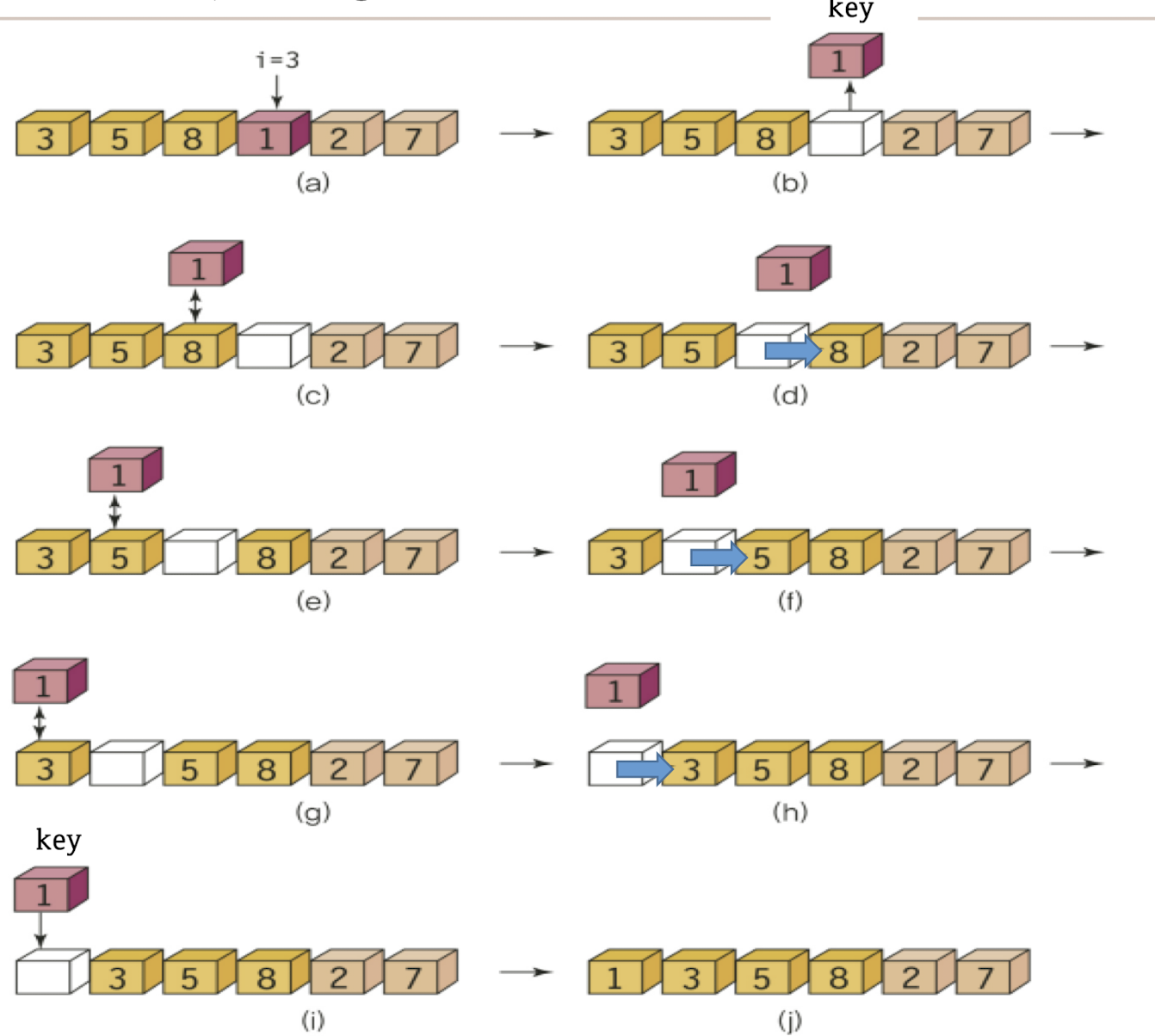
Insertion sort
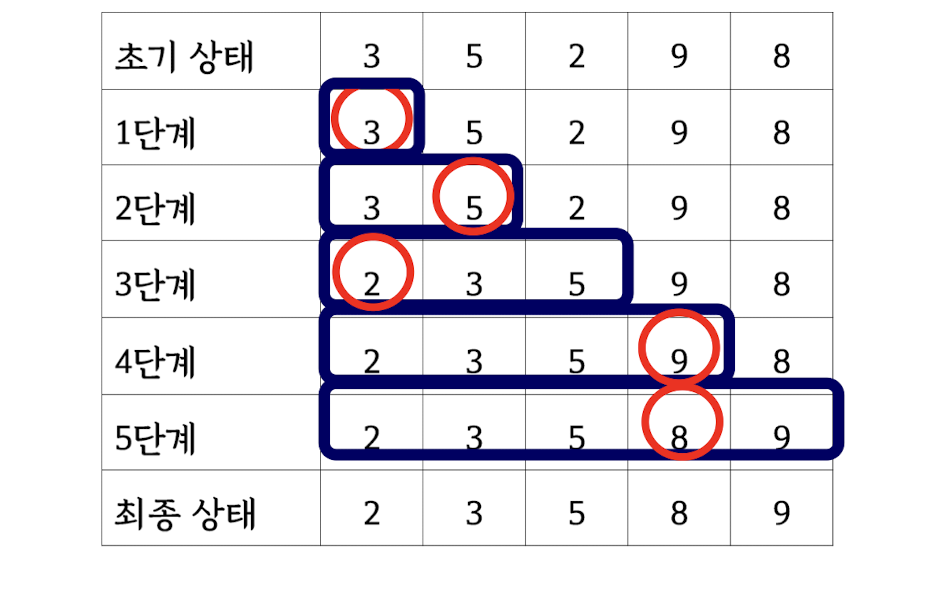


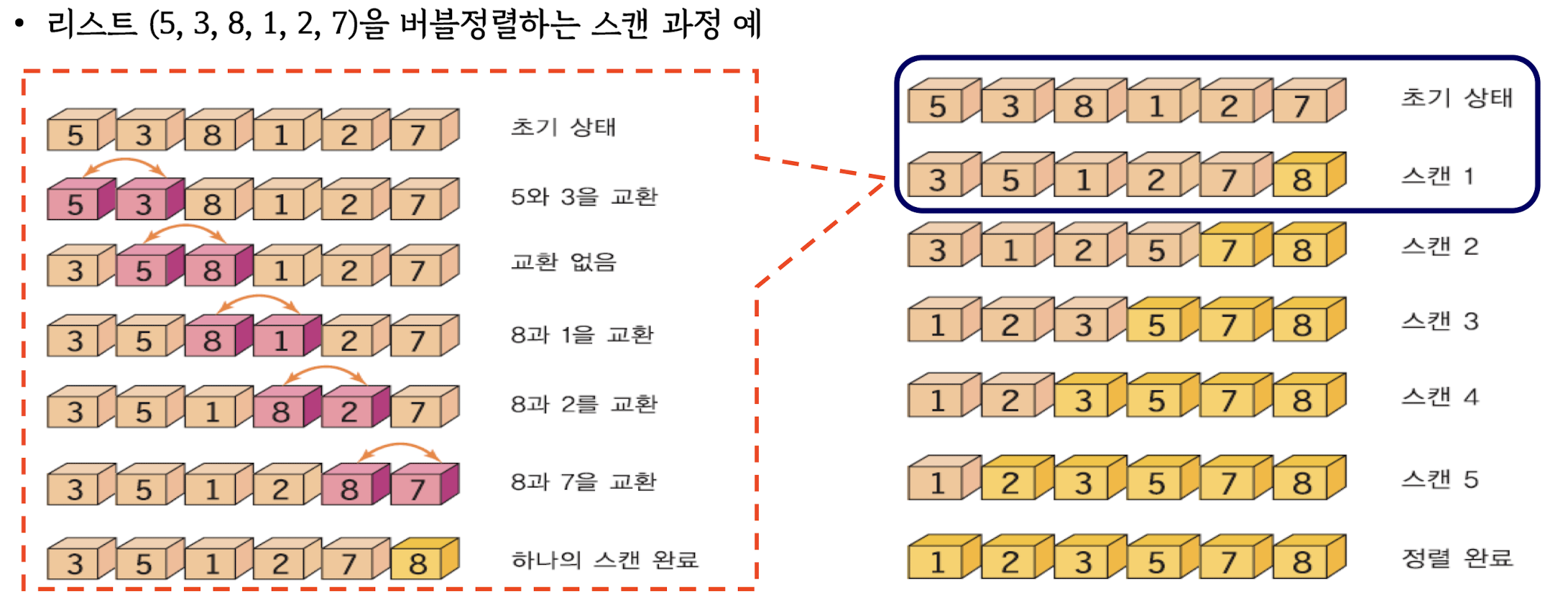
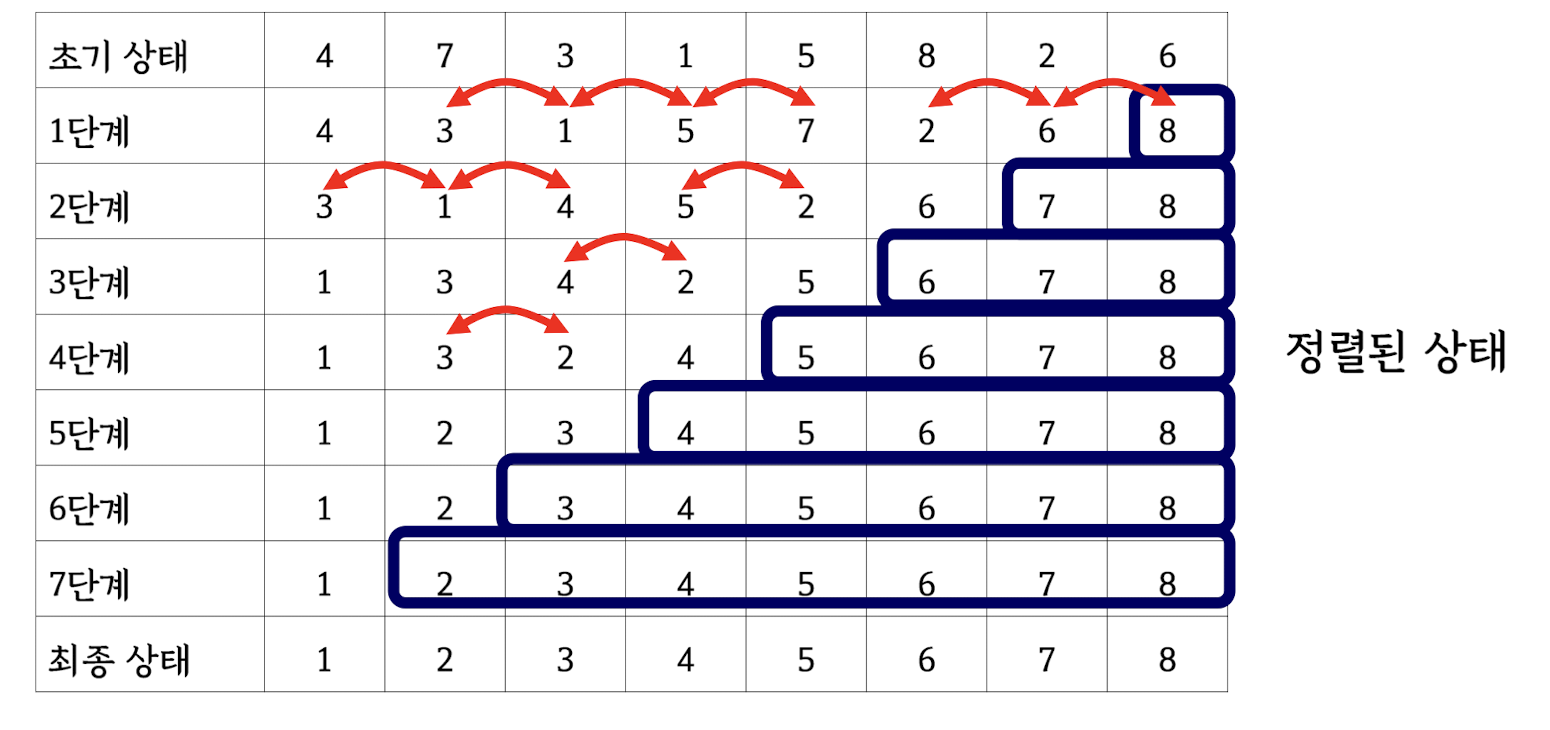
Bubble sort

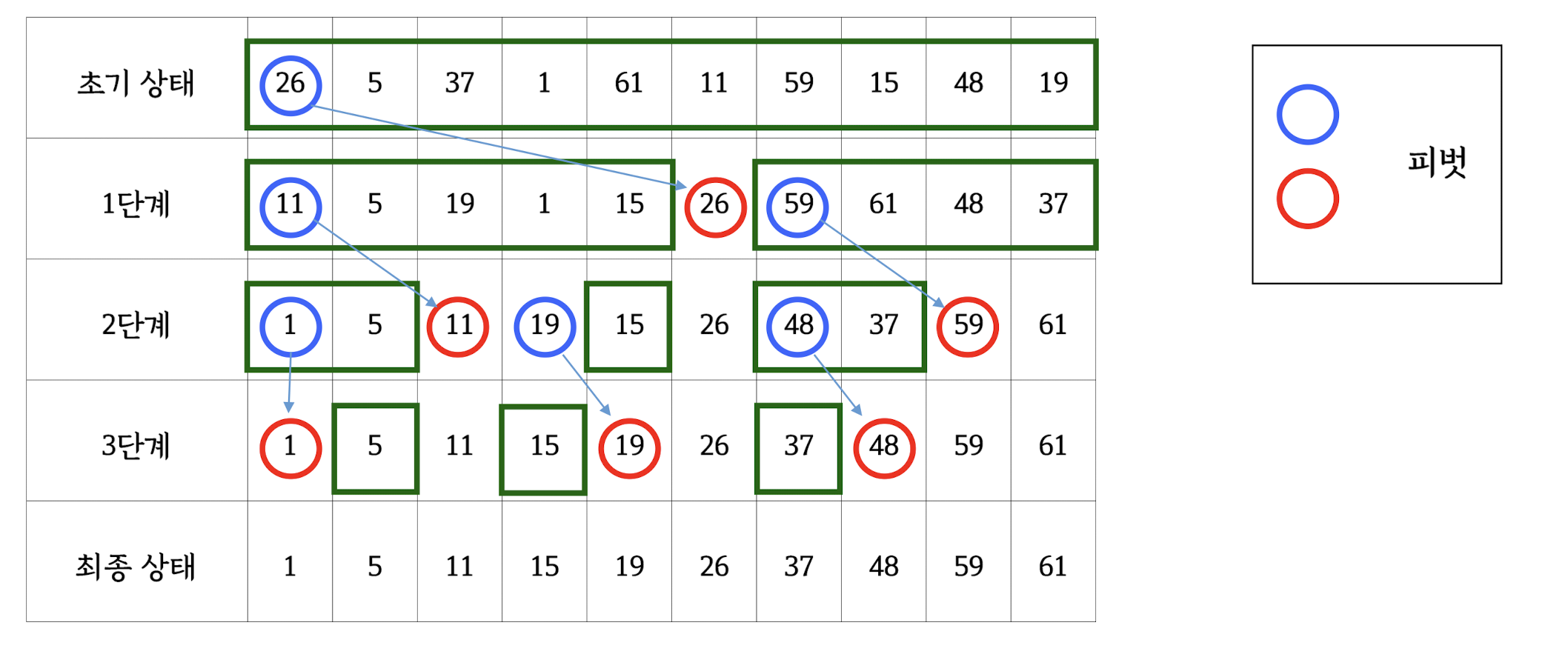
quick sort
* recursion VS tail recursion


Quick sort with stack


Quick sort with stack (tail recursion)
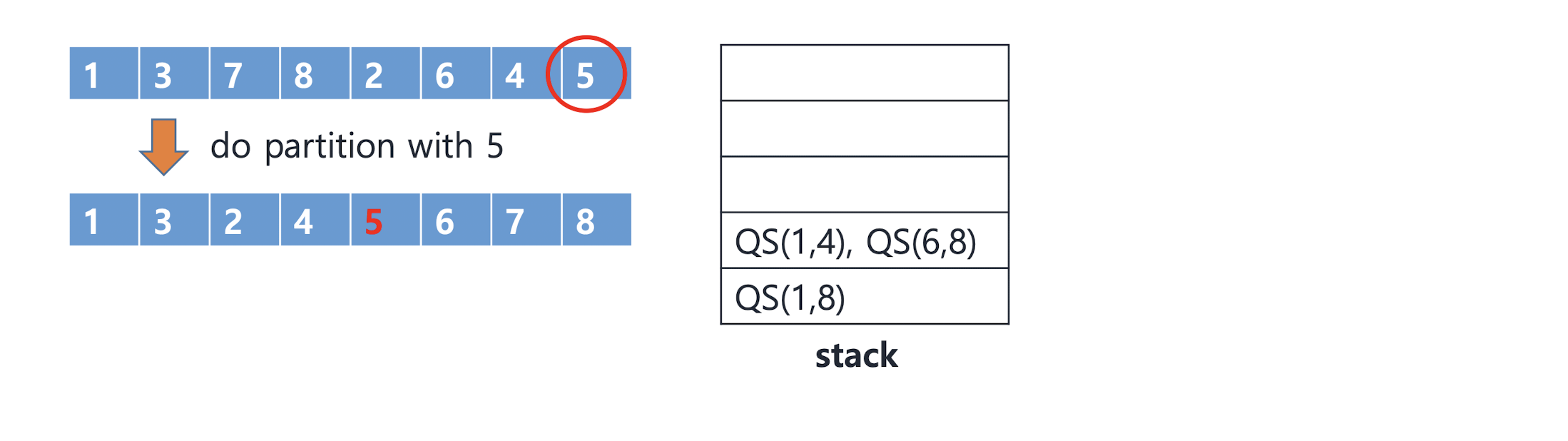
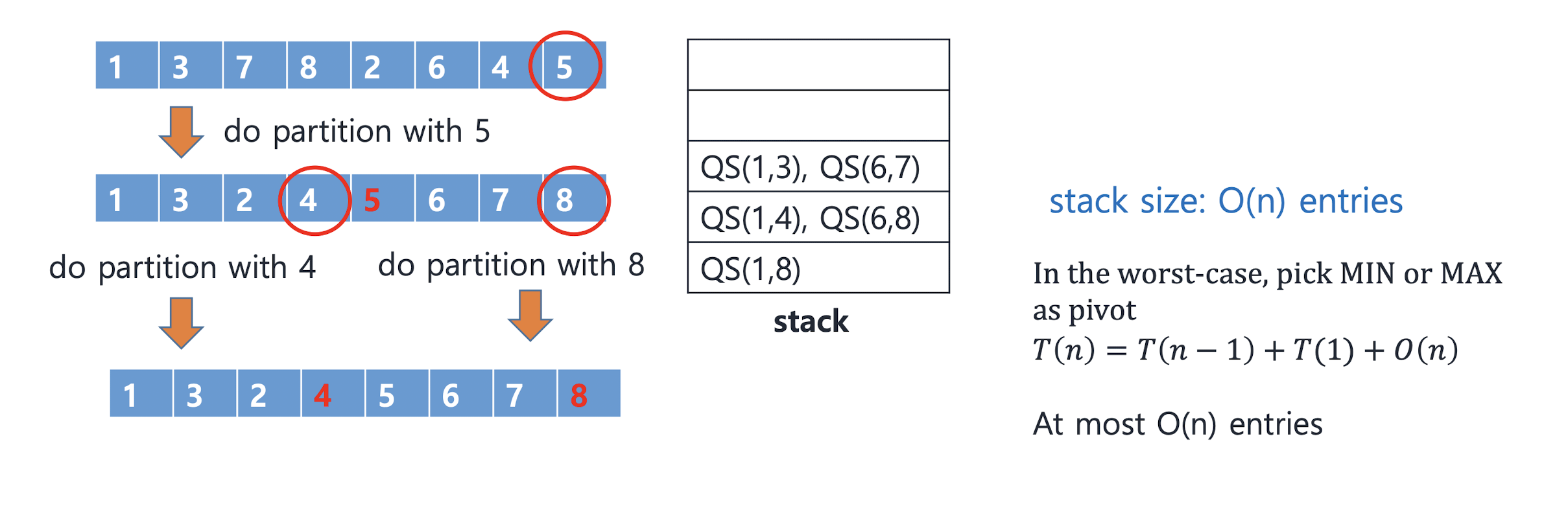
Quick sort with stack (better approach)


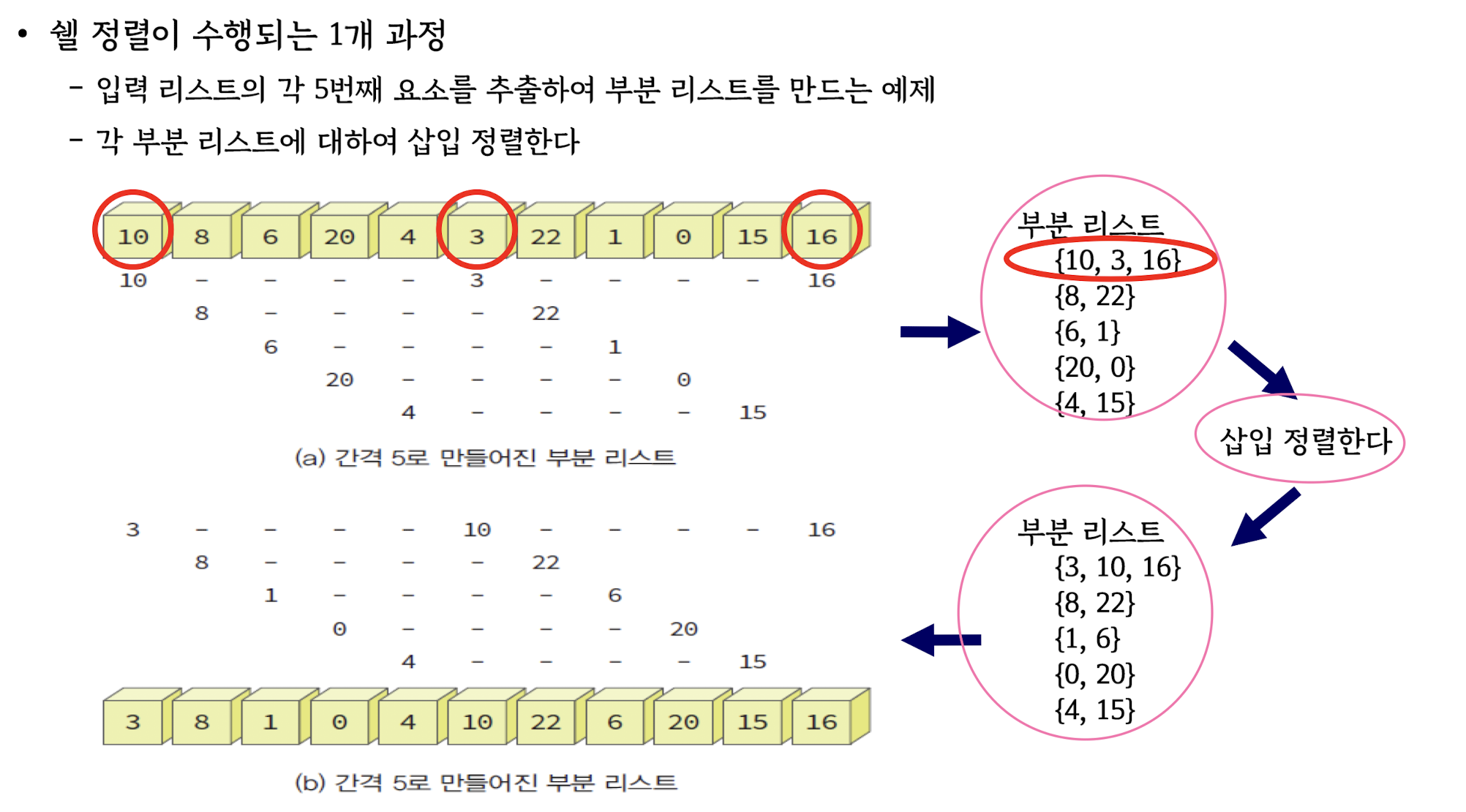
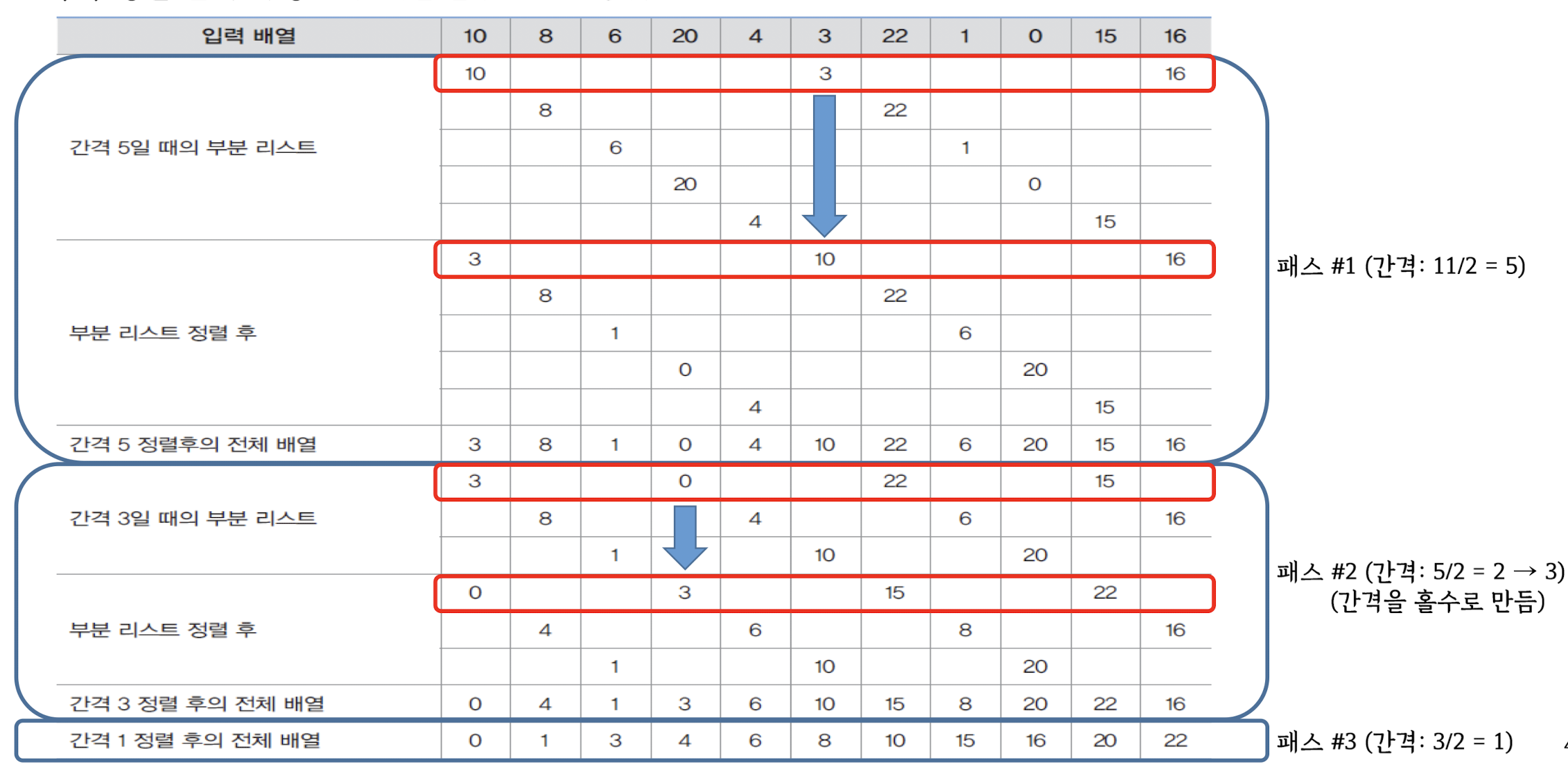
Shell Sort
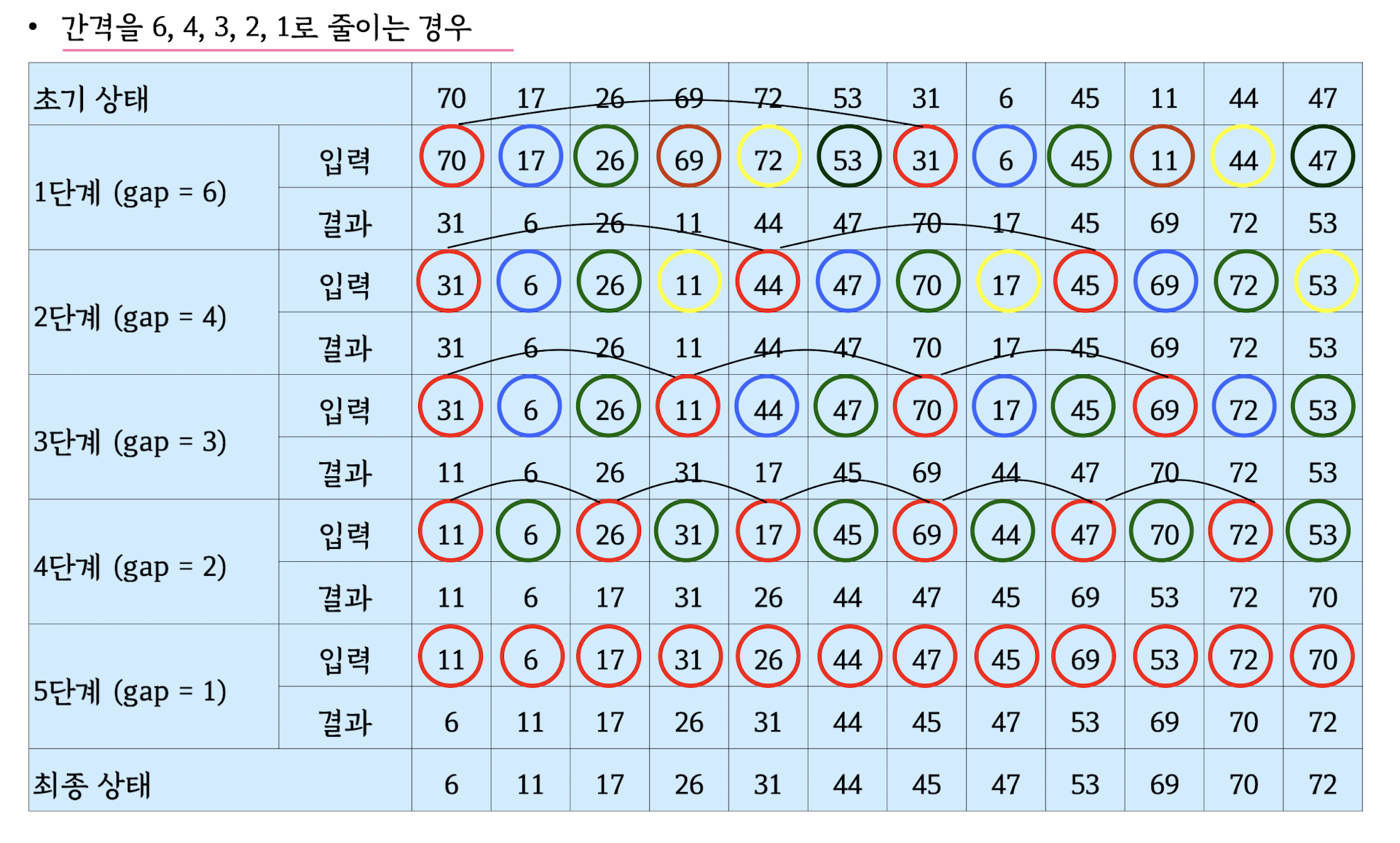
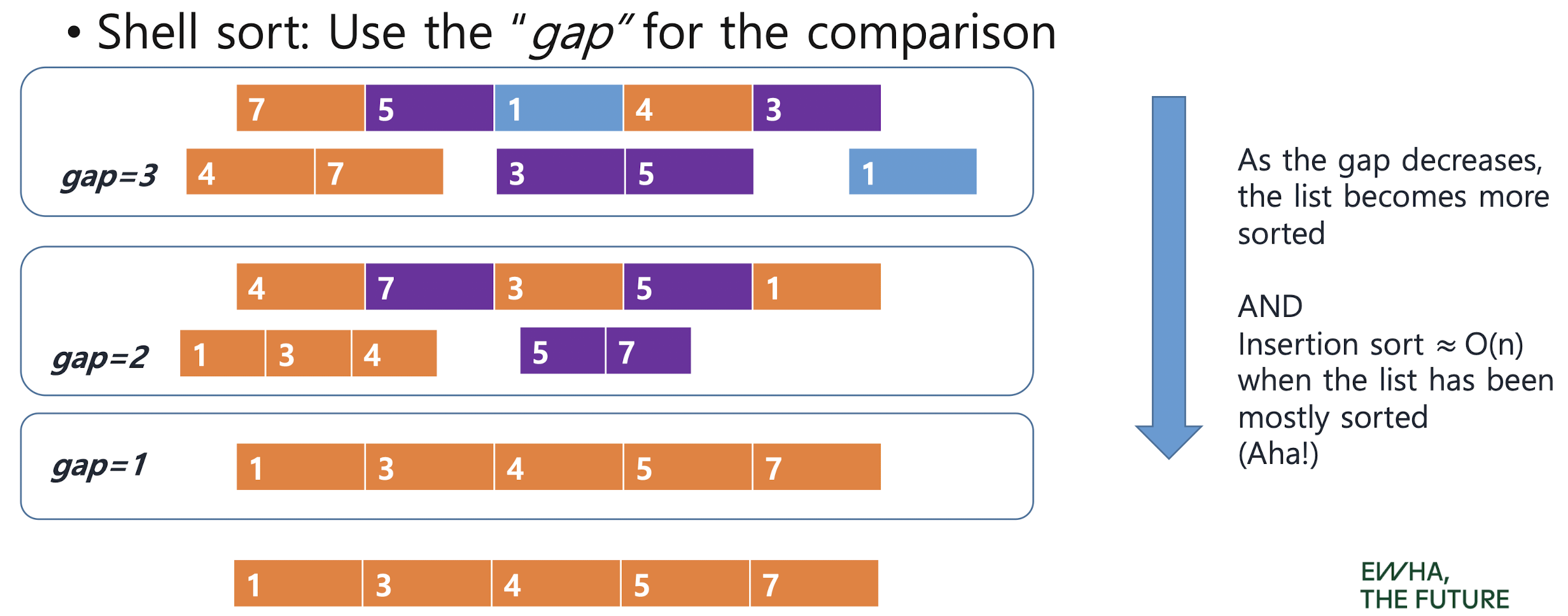

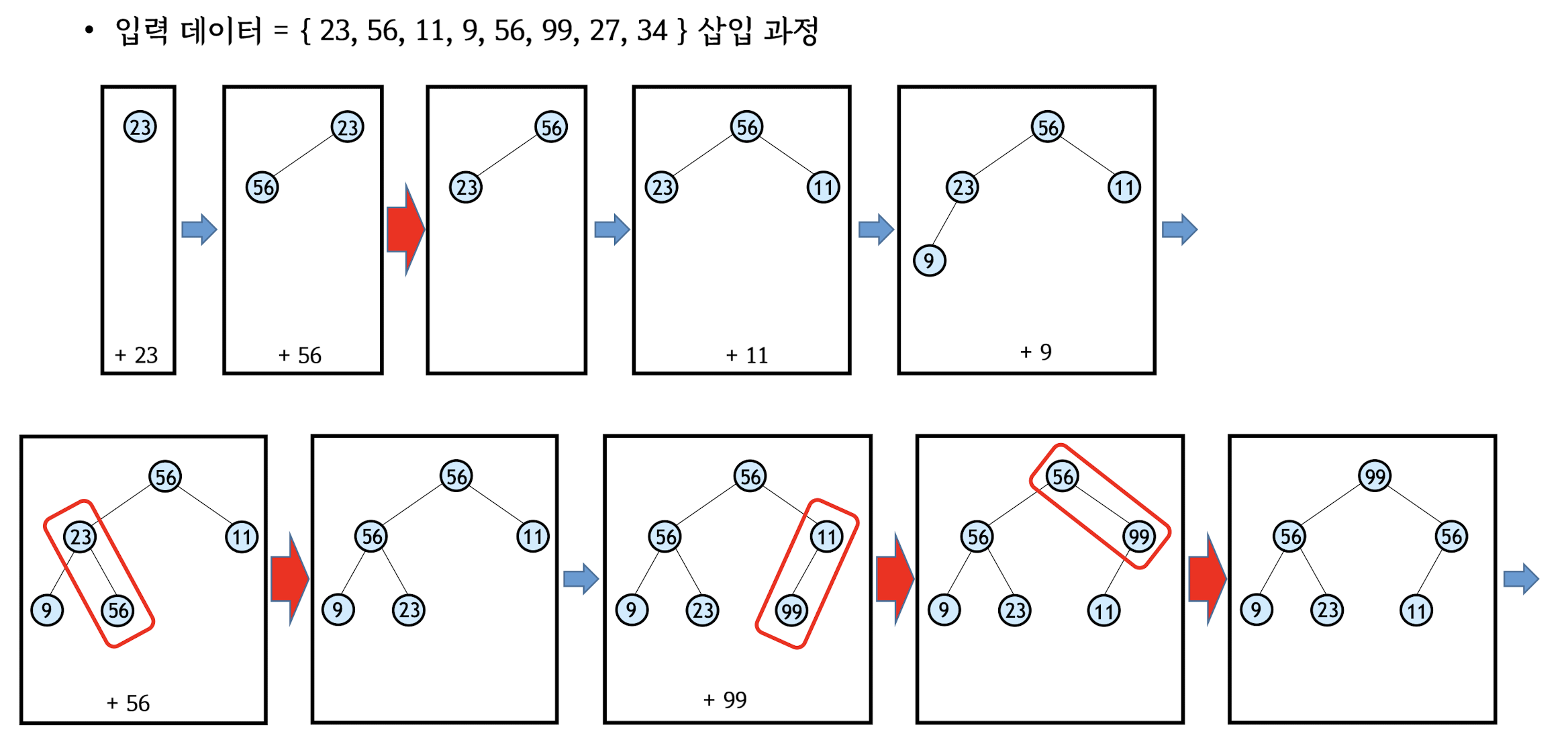
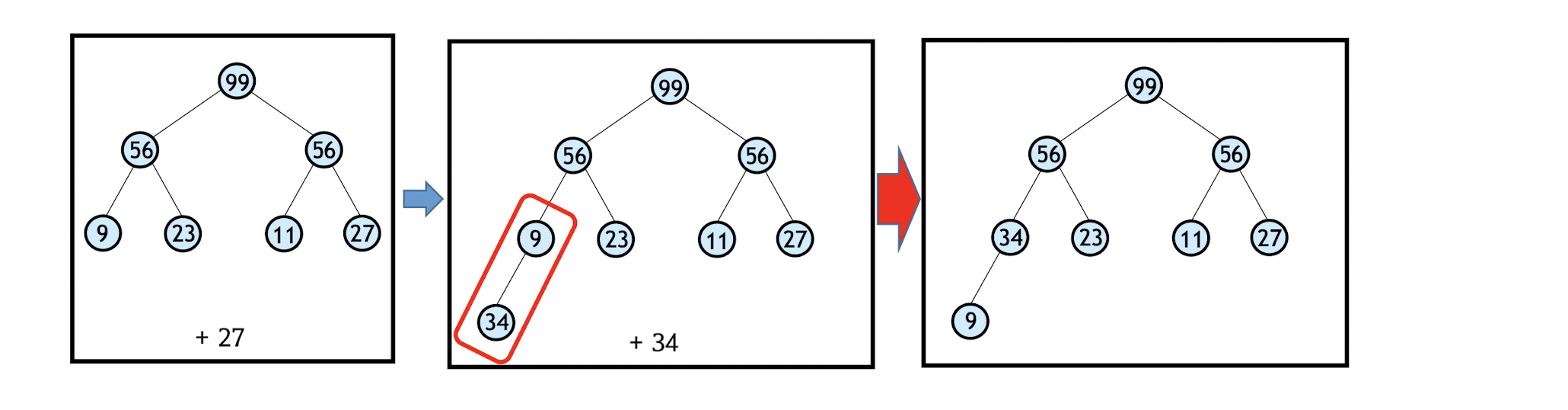
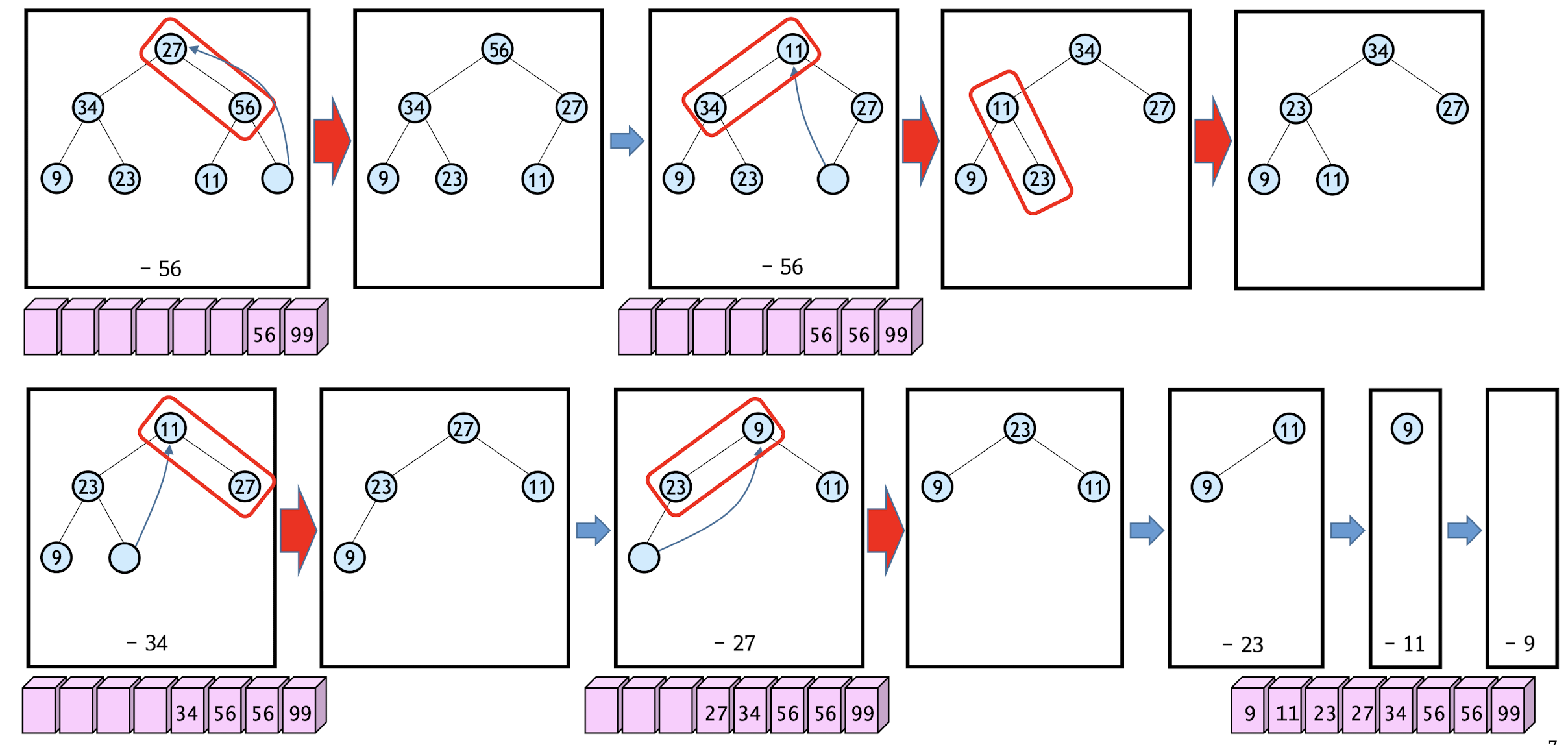
Heap Sort - max-heap (priority queue)
* Heap

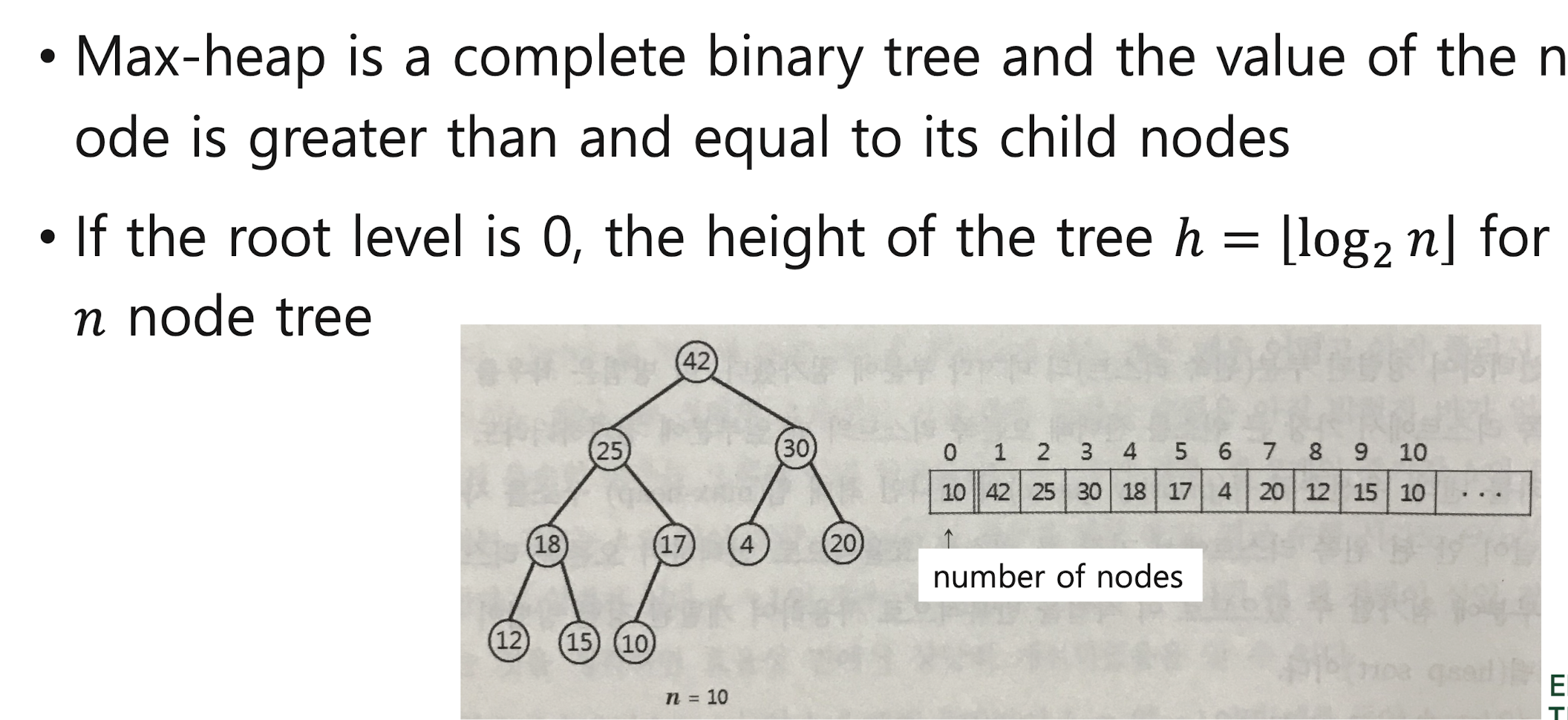
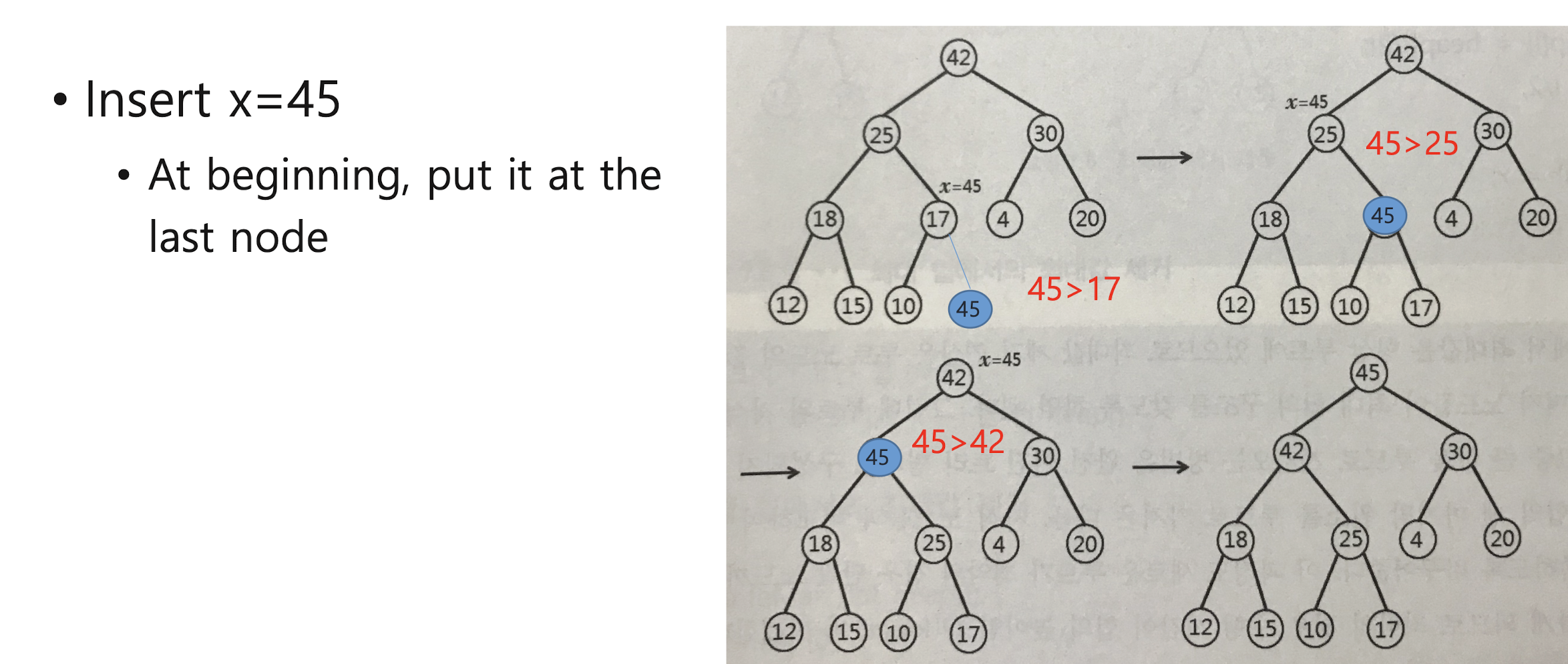
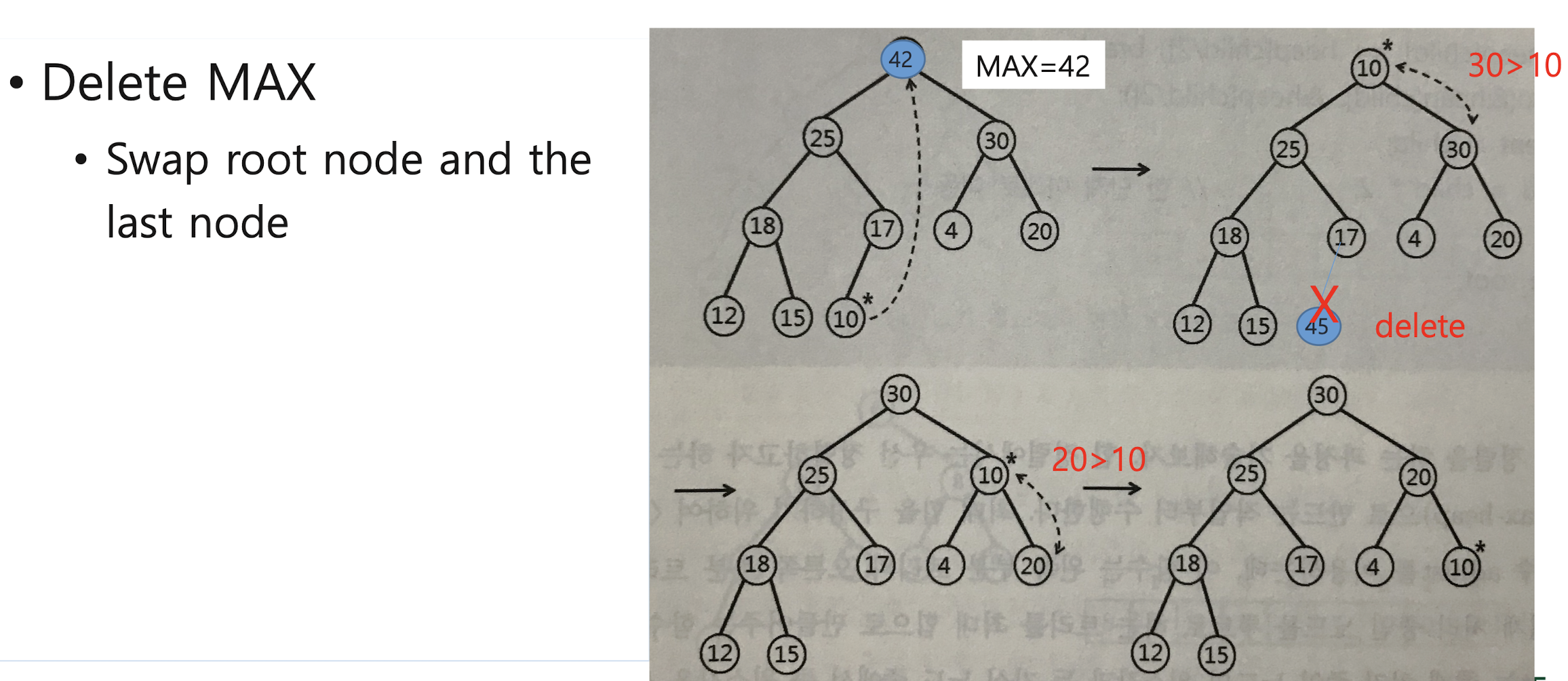
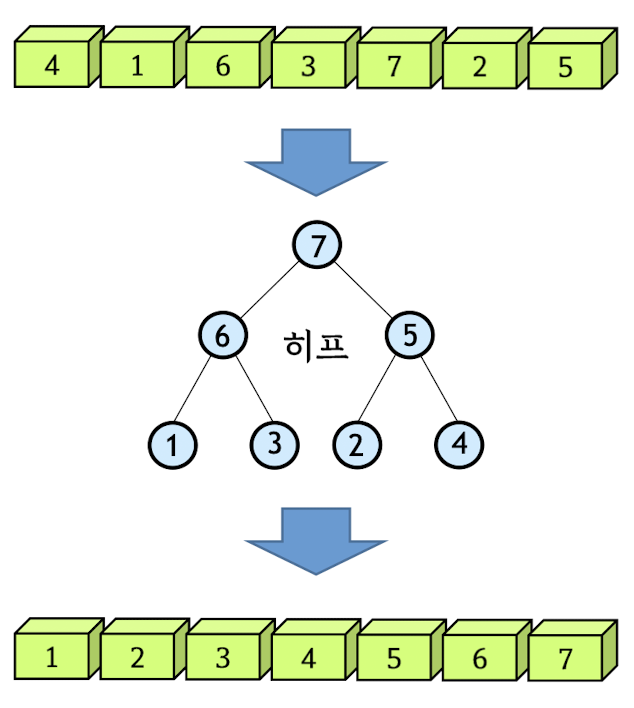
1. First step: construct initial max-heap
2. Second step: Swap the root node and the last node, and re-construct max-heap

Bucket Sort


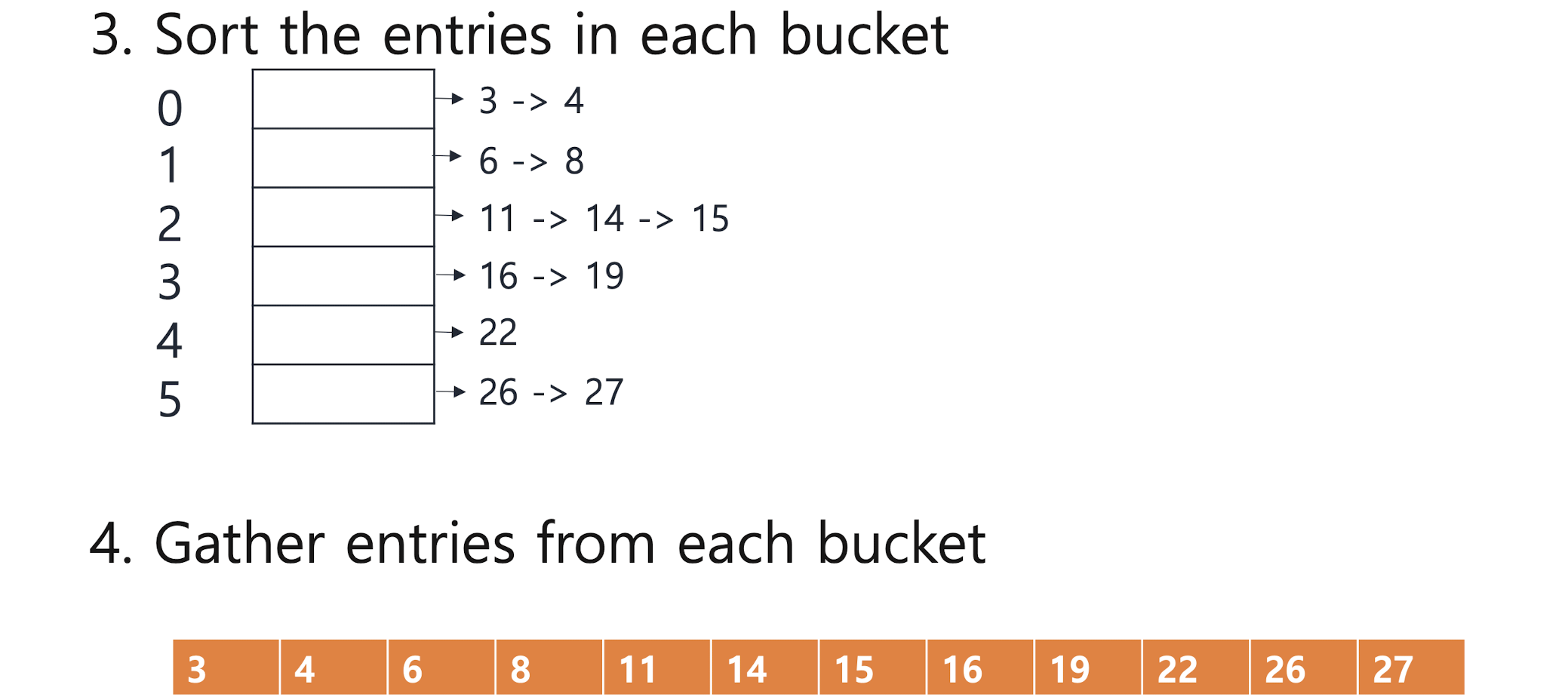

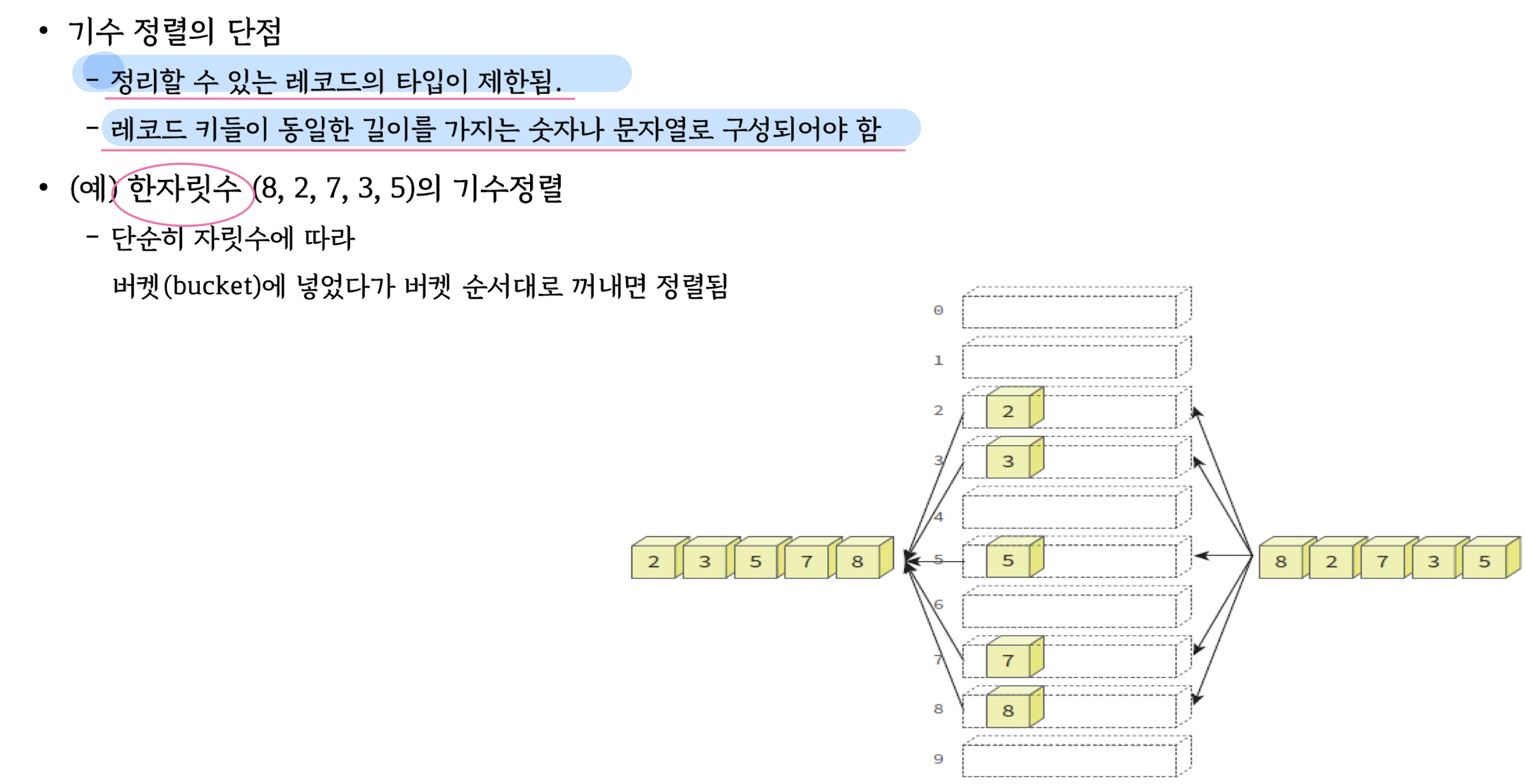
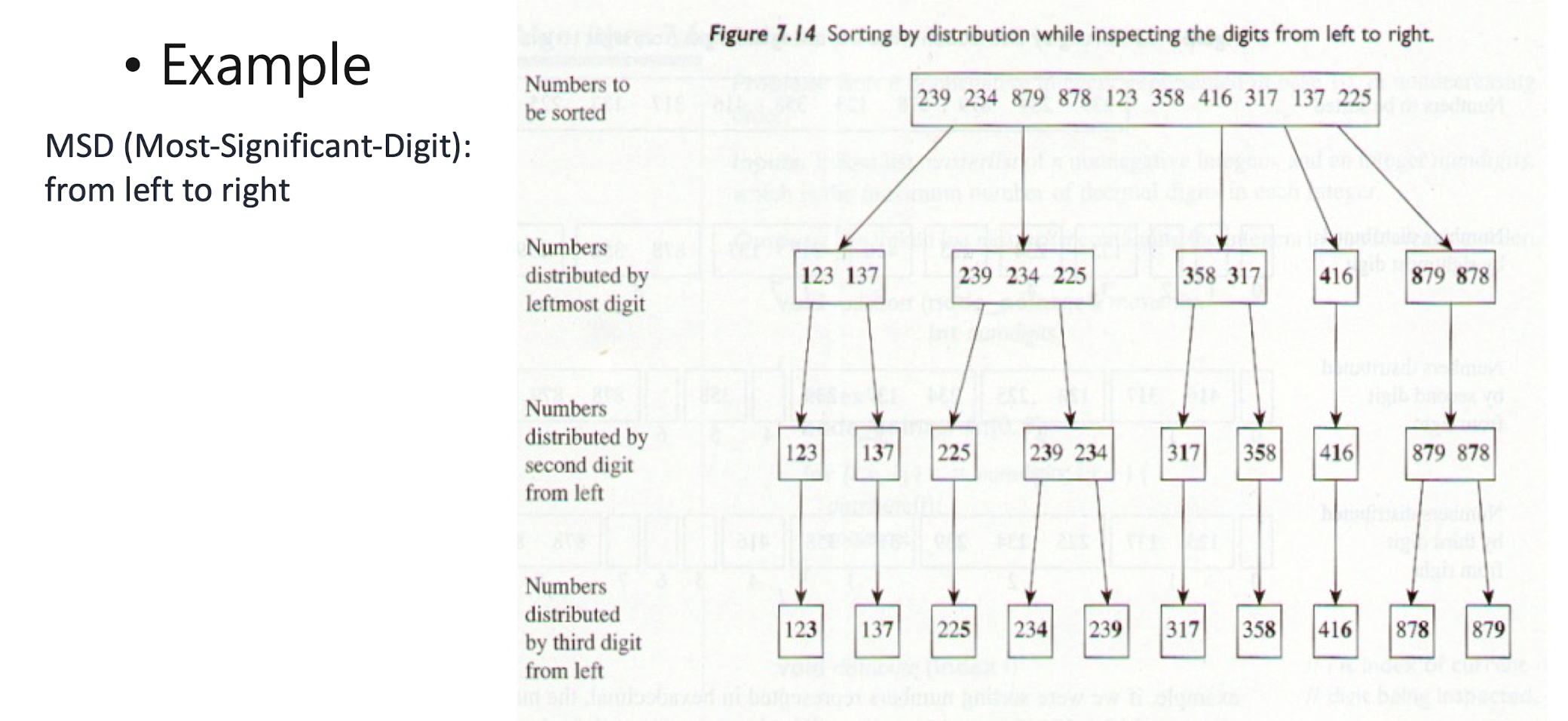
Radix Sort
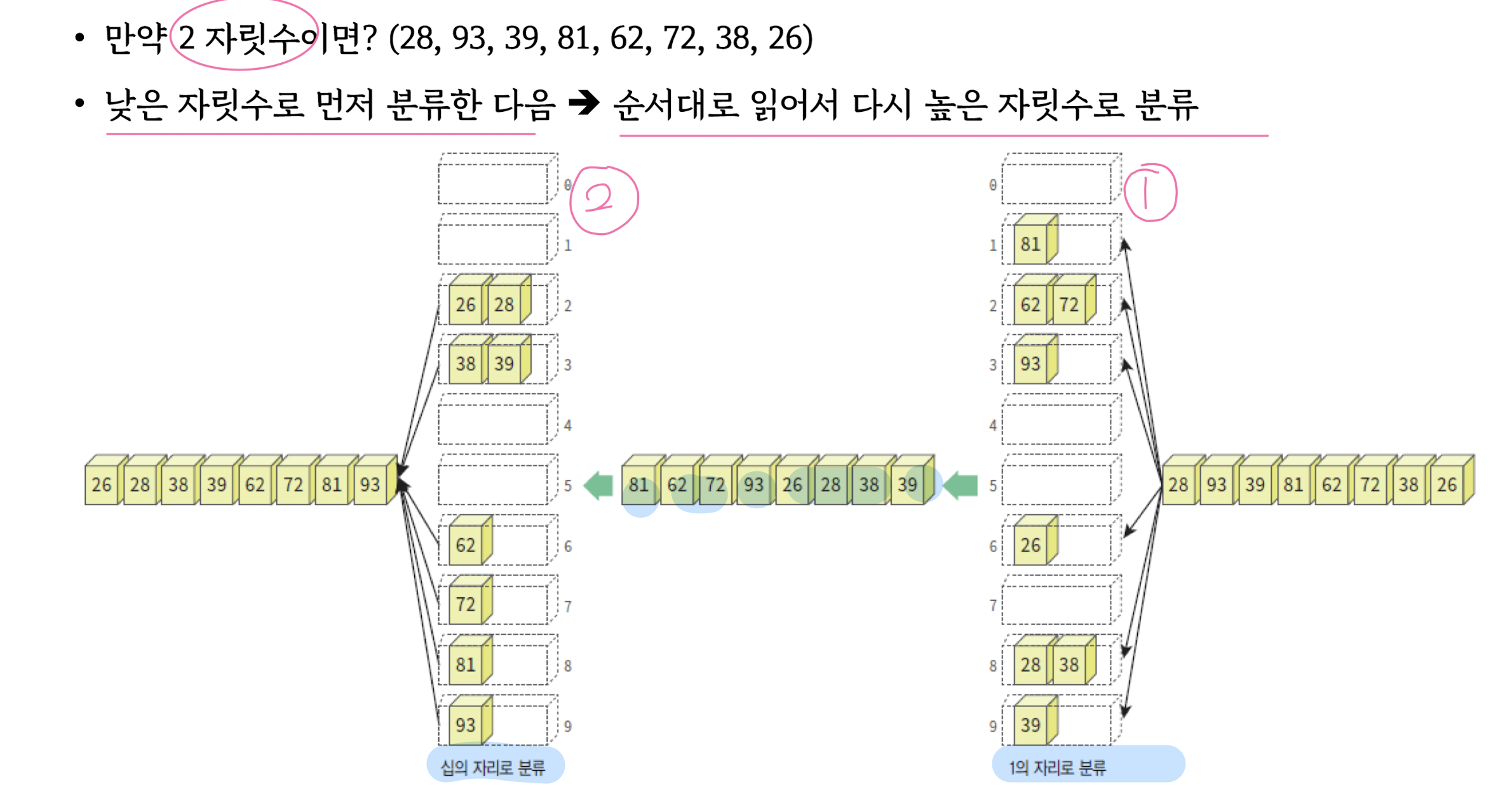
Radix Sort 




Searching

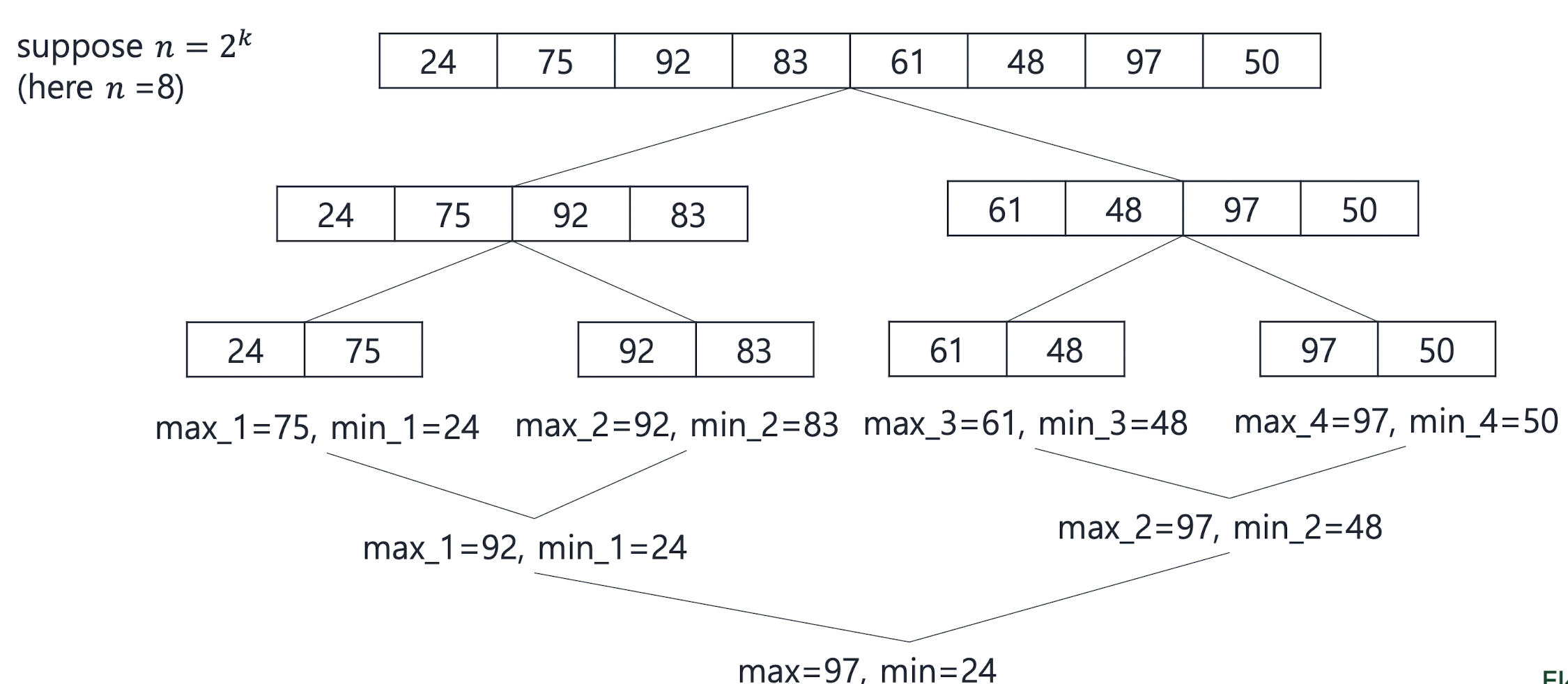
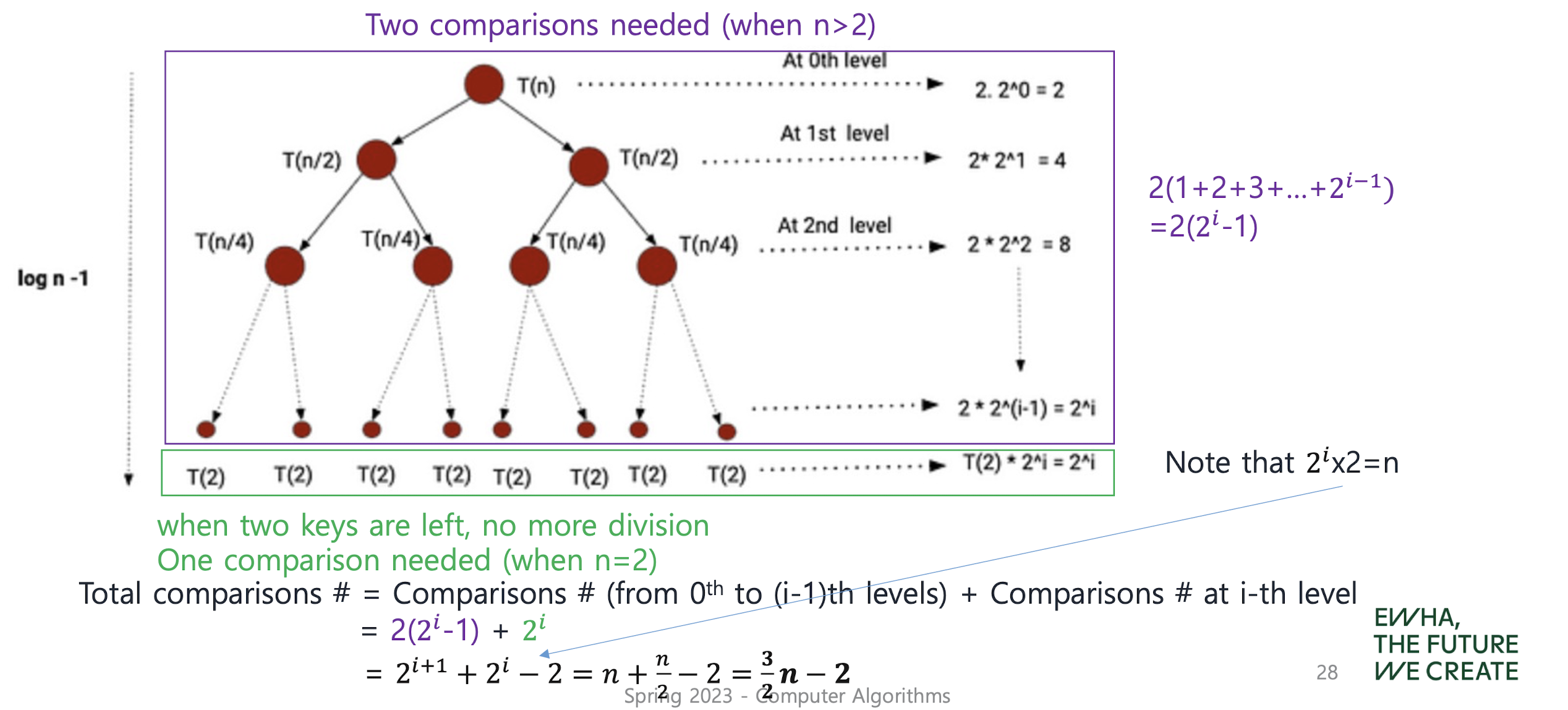
findMinMax


find2ndMax

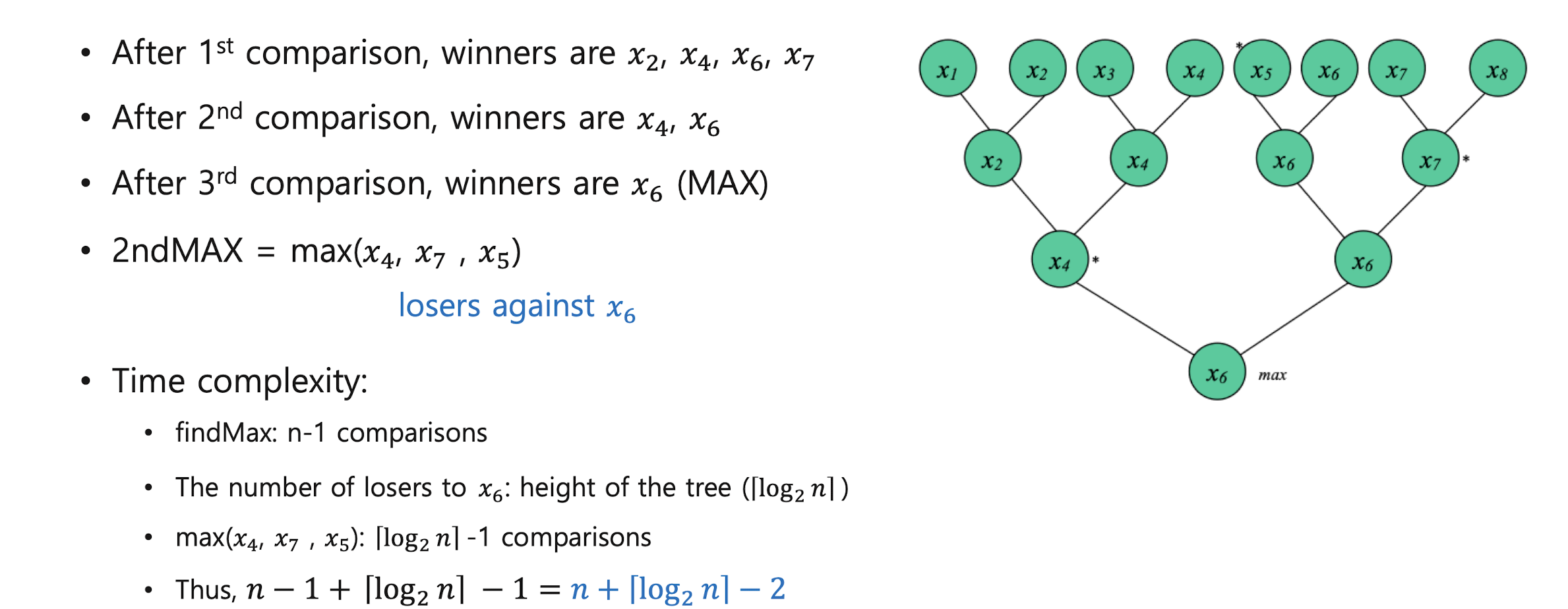
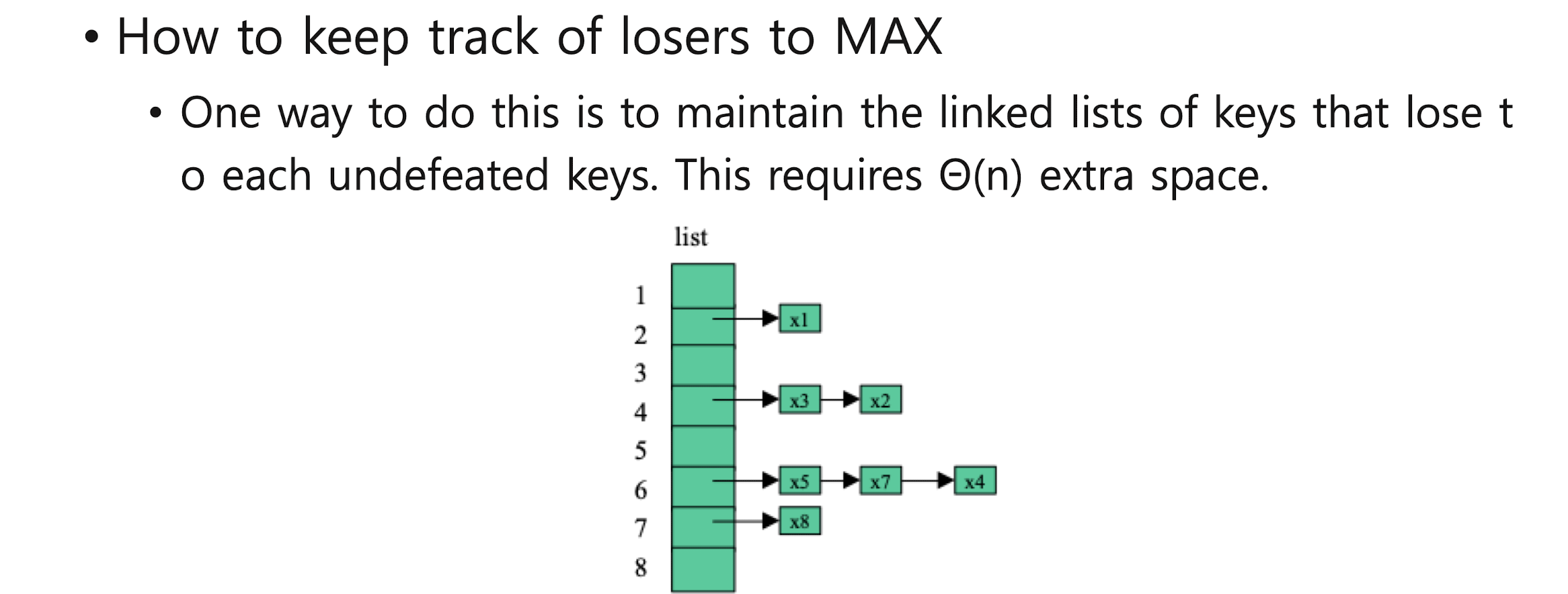
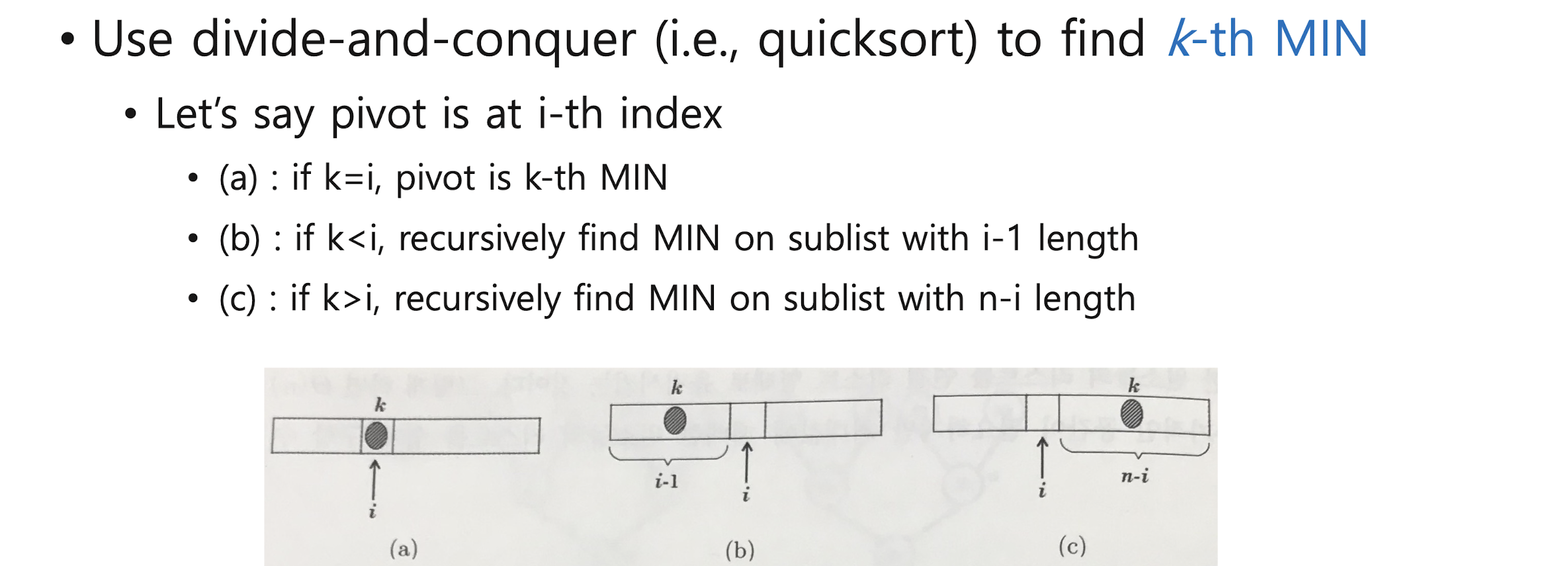
General Selection Algorithm

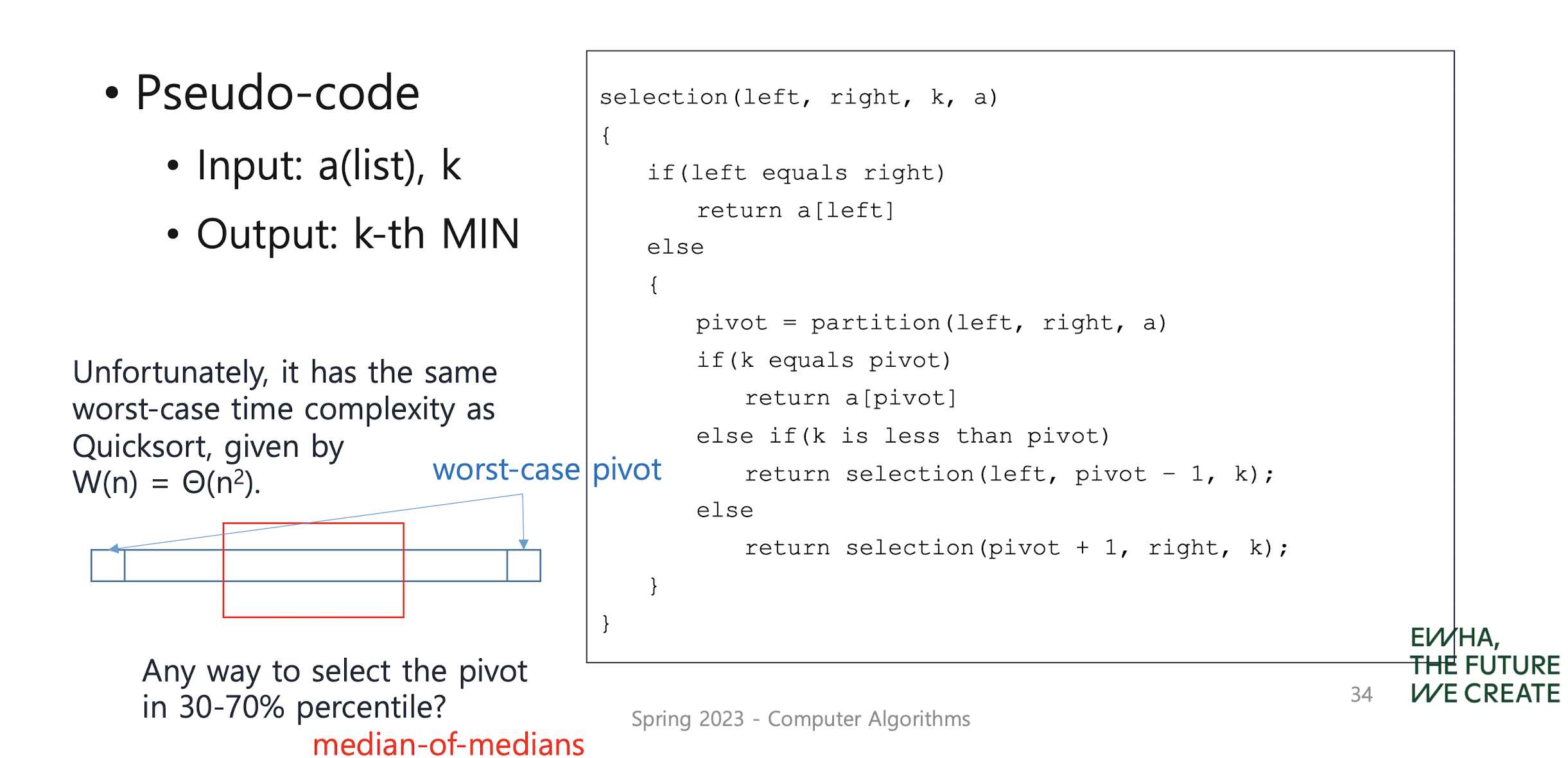

- median-of-medians rule
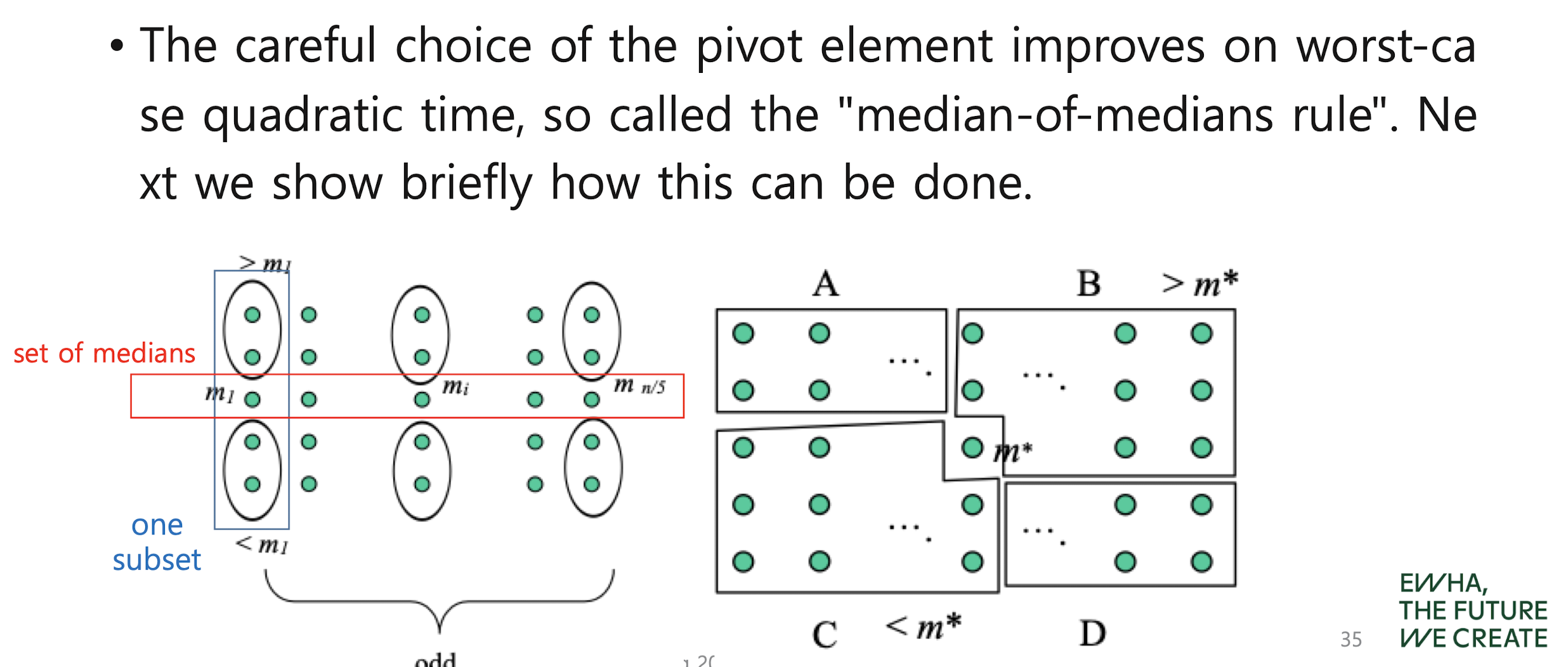
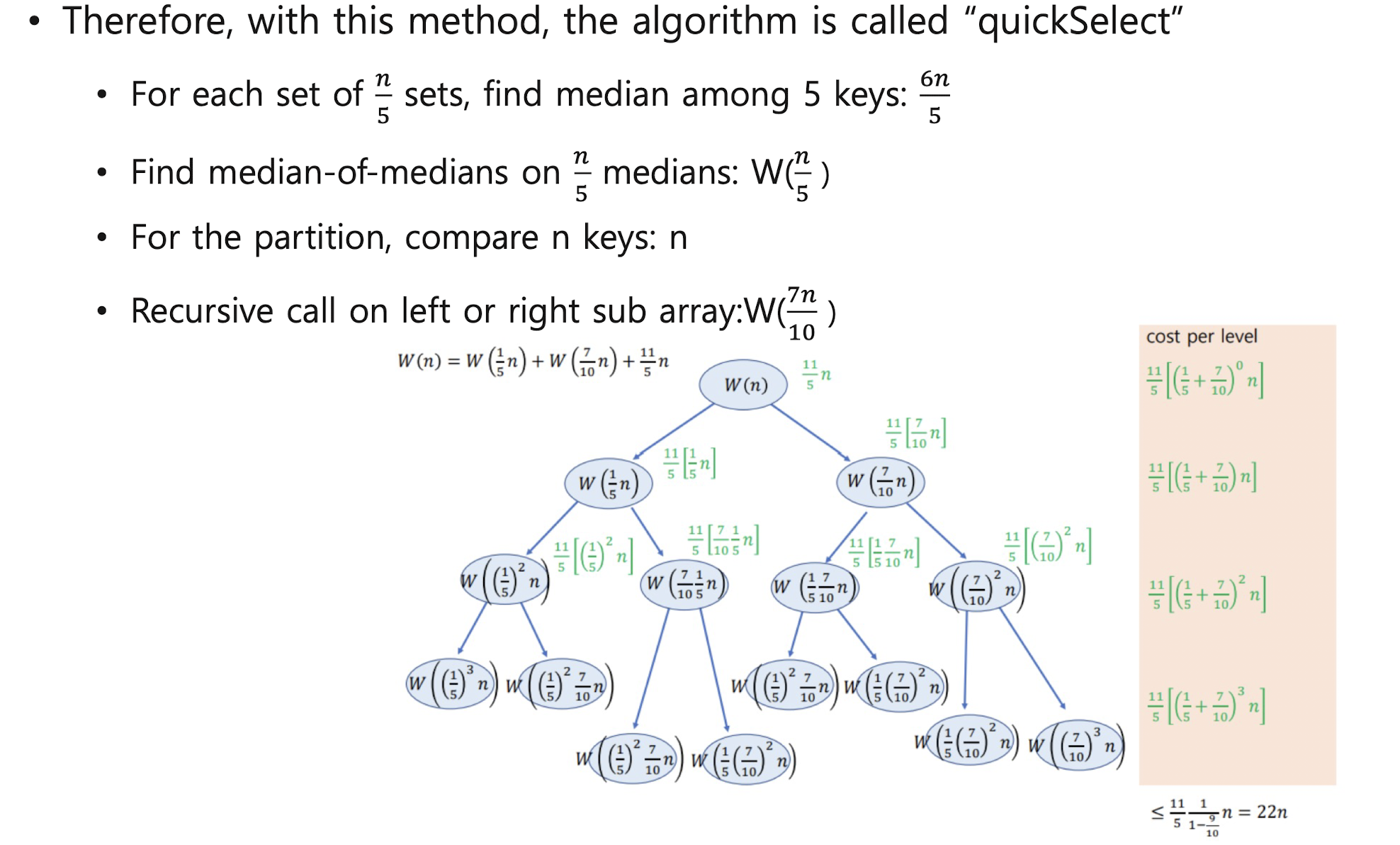



8. Number theory and cryptographic algorithms
정수론 기초
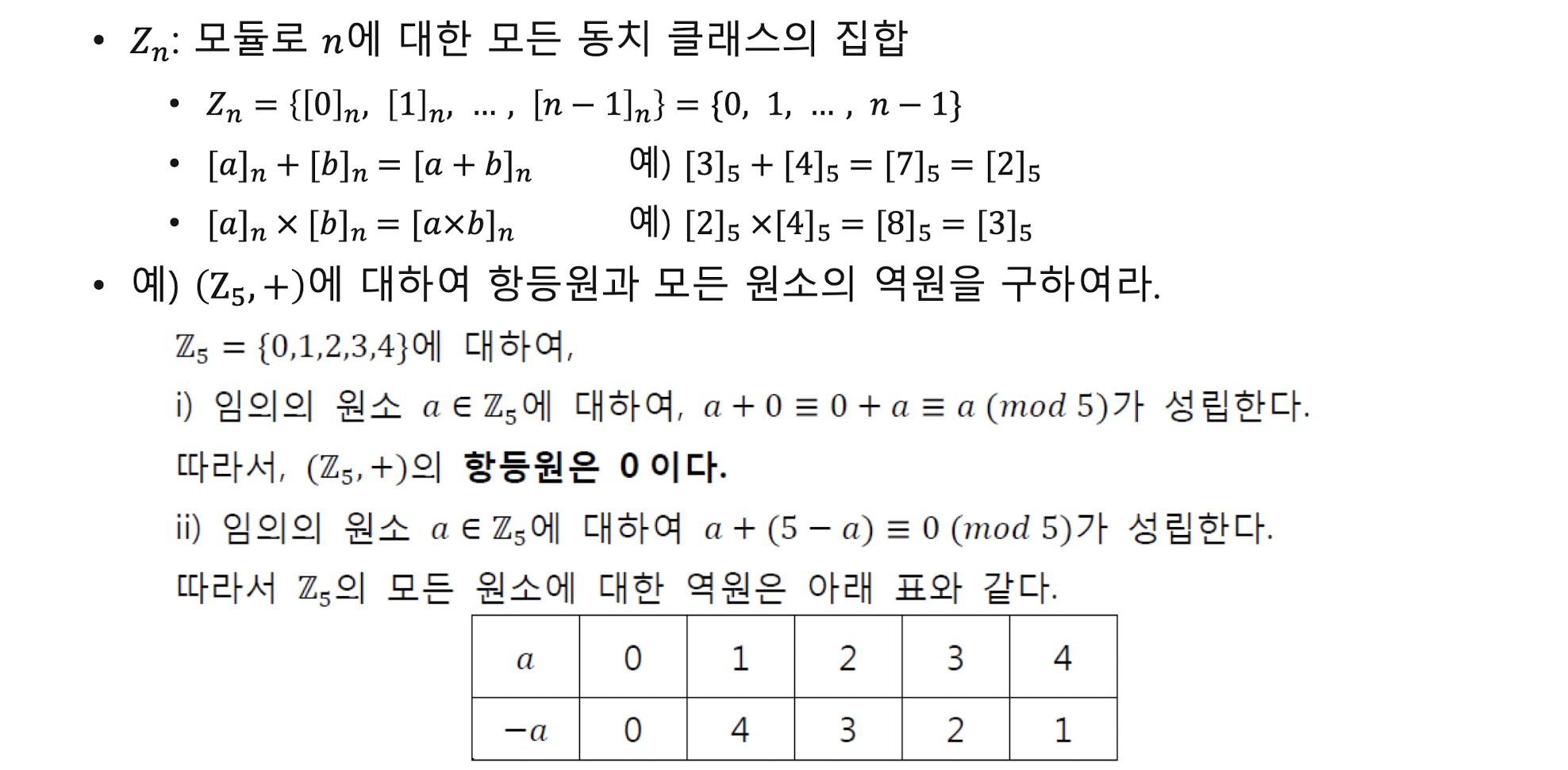
군 Group


동치 관계



정리



오일러 피 함수


부분군subgruop, 진부분군 proper subgruop, 생성원generative





오일러 정리
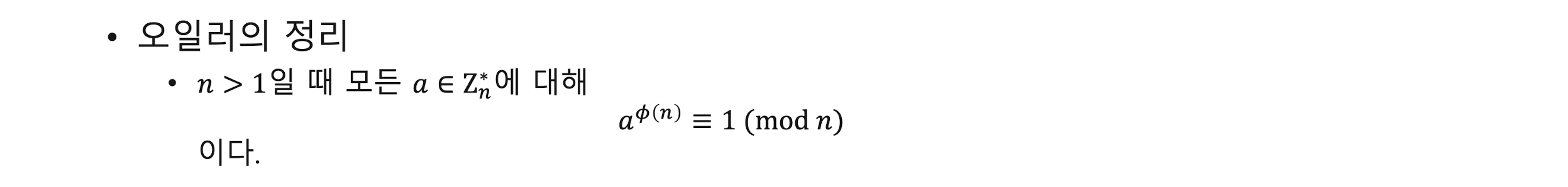


페르마의 소정리 Fermat's little theorem

원시근 Primitive root

이산대수 문제 discrete logarithm problem

유클리드 알고리즘







Cryptographic Algorithms and Protocols
Symmetric (Private) Key Cryptography

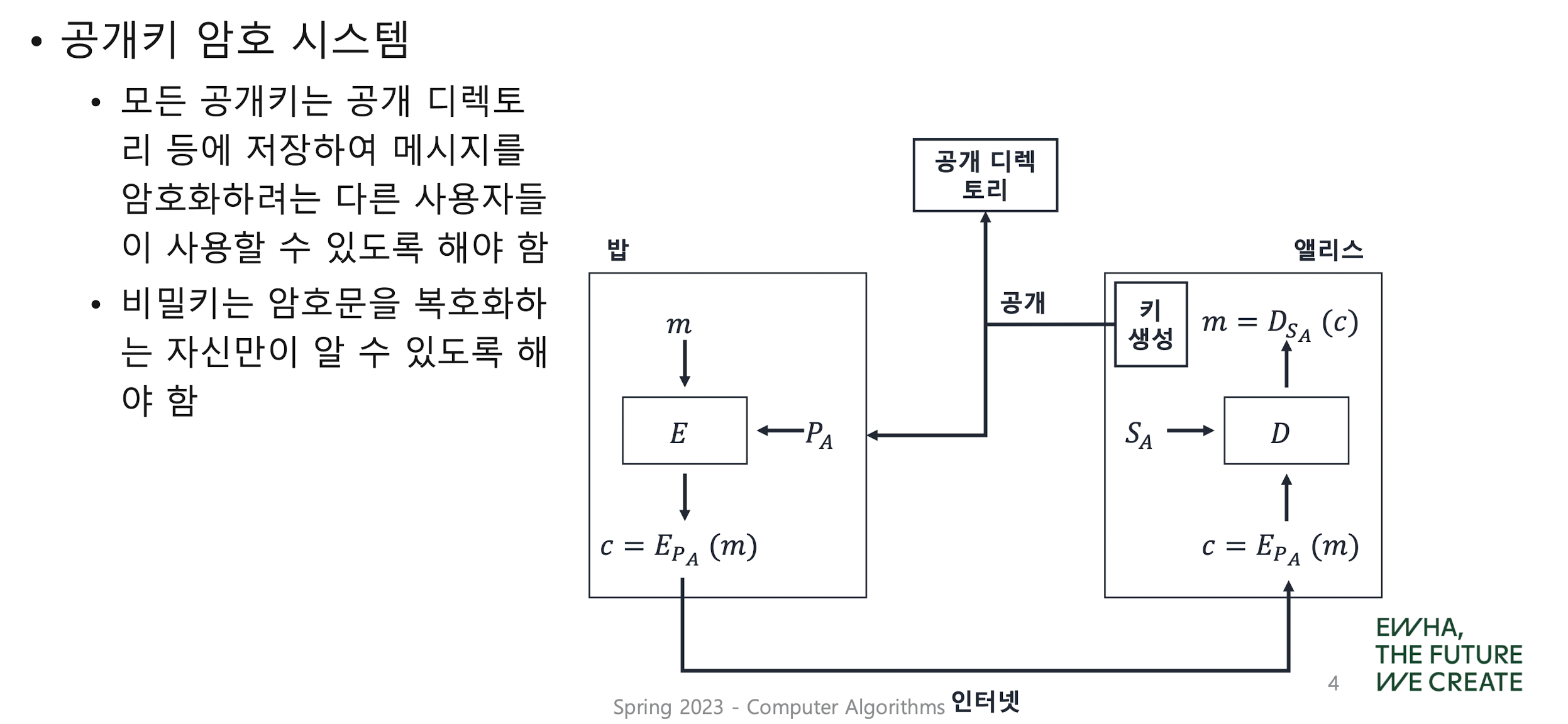
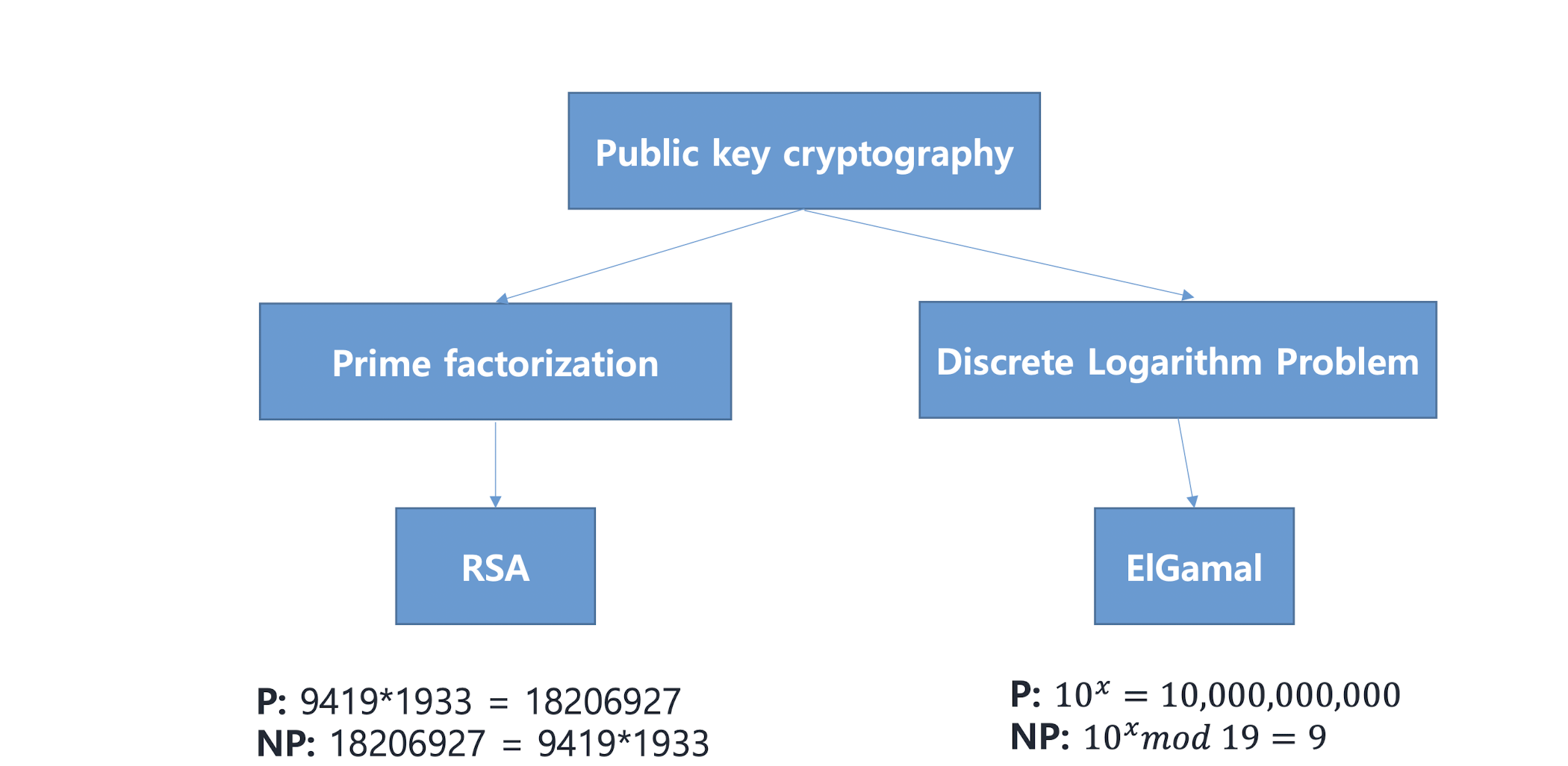
Public Key Cryptography

Merkle-Hellman Knapsack




Public Key Cryptography (Merkle-Hellman Knapsack Algorithm)



RSA scheme


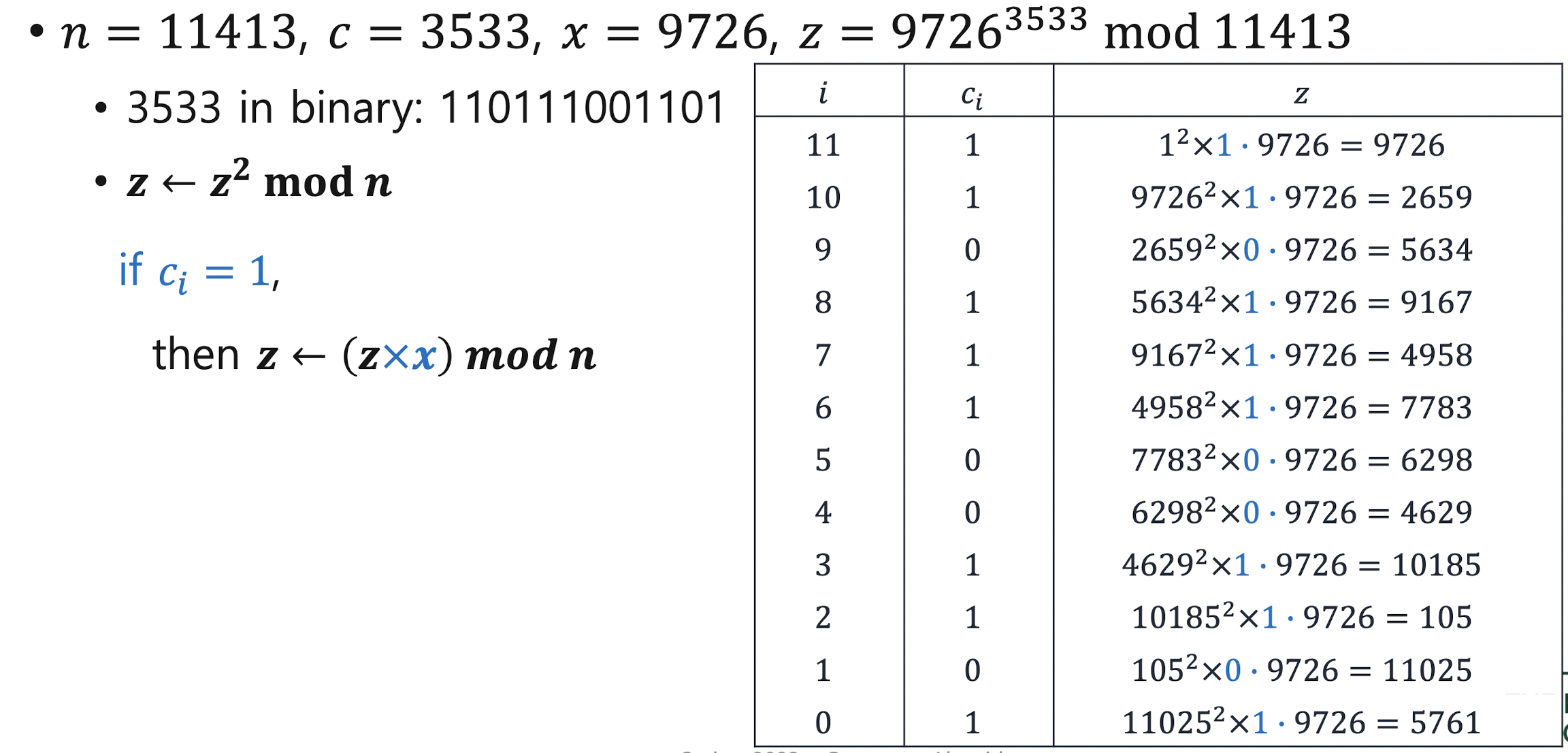
- Square-and-multiply Method



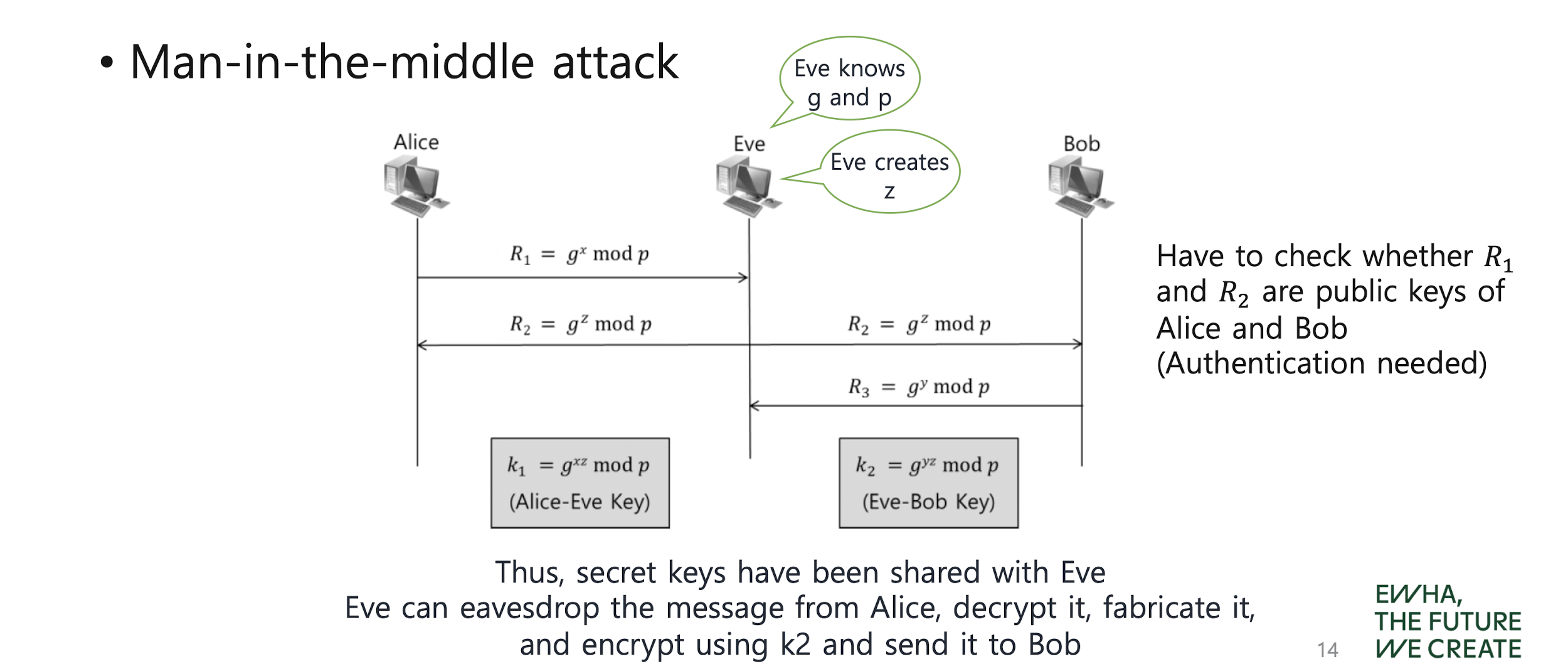
Key Exchange or Establishment
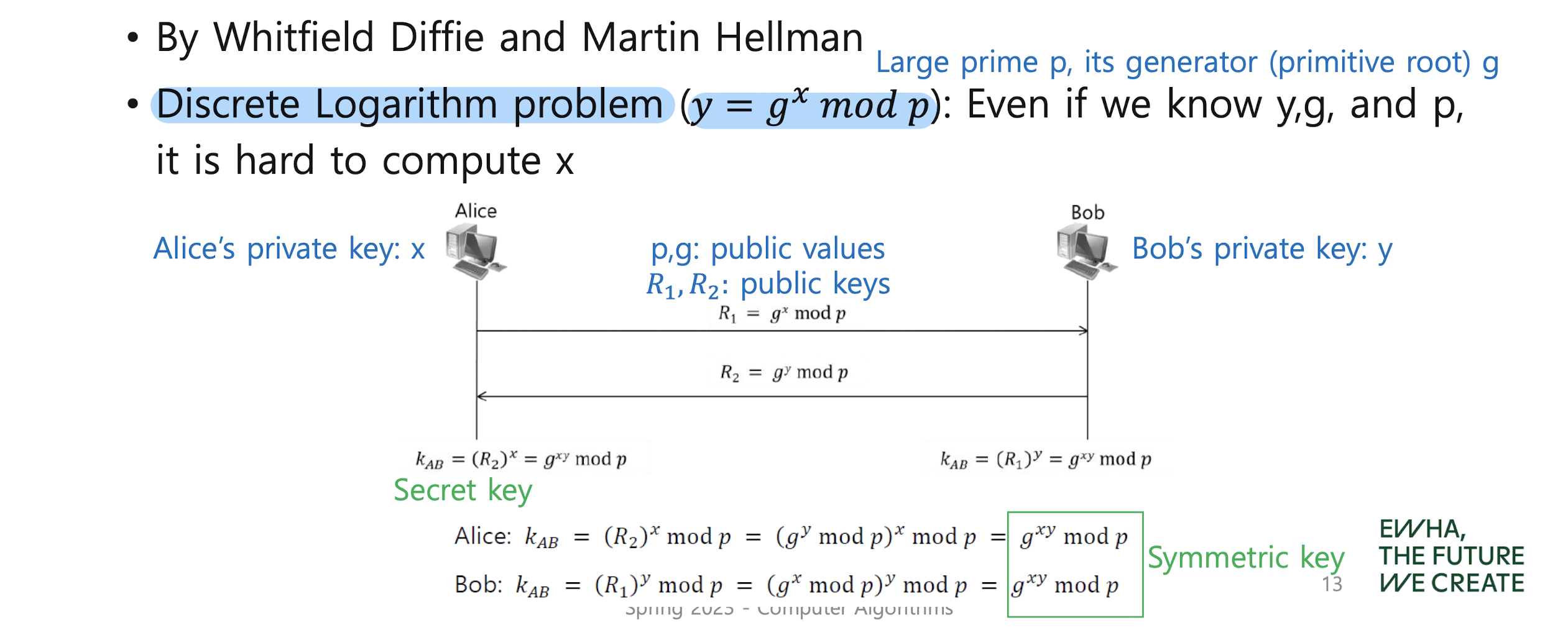
Diffie-Hellman key exchange protocol
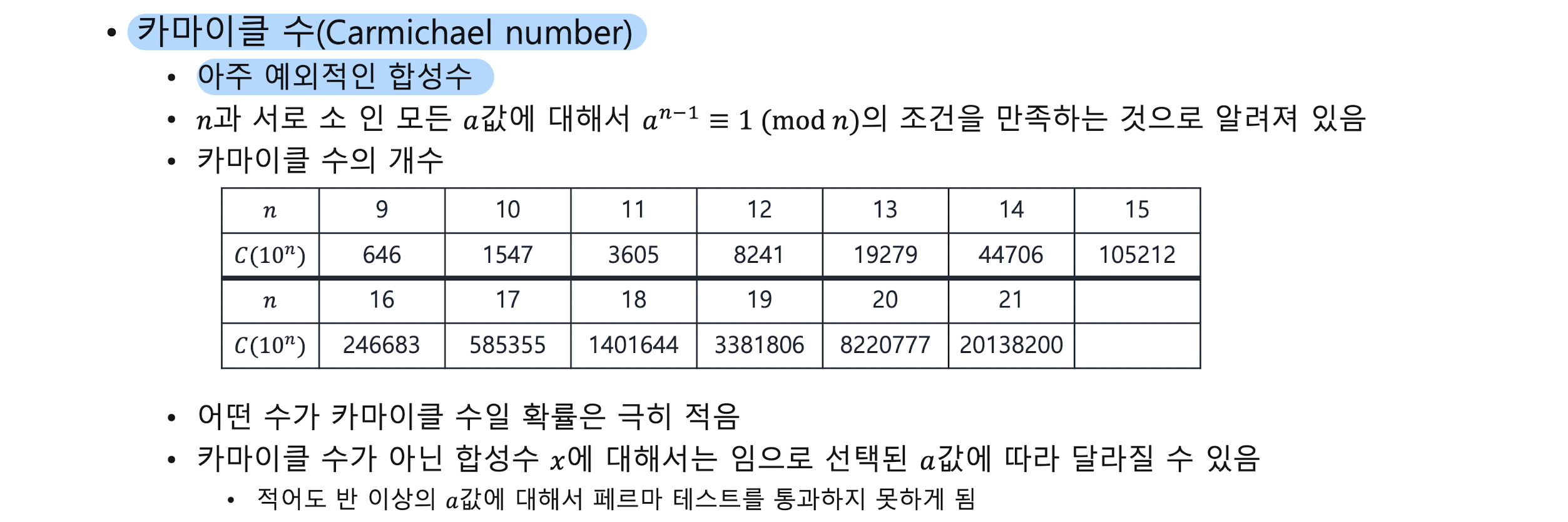
Prime and Primality test





ElGamal 암호 시스템









