백준1300번

백준2512번과 마찬가지로 binary search Algorithm을 적용하는 문제였는데 생각하지도 못한 풀이방법이라 나에게는 어려웠던 문제였다.

# 입력
n = int(input())
k = int(input())

# 문제에서 주어진 nxn 이차원 배열에서 x보다 작은 수의 개수를 구하여 반환하는 함수
def get_num_smaller(x: int) -> int:
    num_smaller = 0
    for i in range(1, n+1):
        # i번째 행에서 x보다 작은 수의 개수는 min(n, (x-1)//i)
        num_smaller += min(n, (x-1)//i)
    return num_smaller

# 문제에서 주어진 nxn 이차원 배열에서 x보다 큰 수의 개수를 구하여 반환하는 함수
def get_num_bigger(x: int) -> int:
    num_bigger = 0
    for i in range(1, n+1):
        # i번째 행에서 x보다 큰 수의 개수는 n-min(n, x//i)
        num_bigger += n - min(n, x//i)
    return num_bigger


# main function
low = 1
high = min(n*n, int(1e9))

# 아직 찾지 못함
answer = -1

while low <= high:
    mid = (low+high)//2
    num_smaller = get_num_smaller(mid)
    num_bigger = get_num_bigger(mid)

    if num_smaller > k-1:
        # mid 보다 작은 수가 너무 많으면 답은 Low~mid-1 사이에 존재한다
        high = mid - 1
    elif num_bigger > n*n - k:
        # mid 보다 큰 수가 너무 많으면 답은 mid+1~high 사이에 존재한다
        low = mid + 1
    else:
        # mid 보다 작은 수가 k-1개 이하이고 큰 수가 n-k개 이하이면 mid는 k번째 수이다
        answer = mid
        break
print(answer)

•Algorithm
x가 k번째 수라고 했을 때 하나의 row 내에서

• x보다 작은 수는 k-1개 이하이다
• x보다 큰 수는 N^2-k개 이하이다

Ex) Let N = 5(5x5 matrix), k = 17

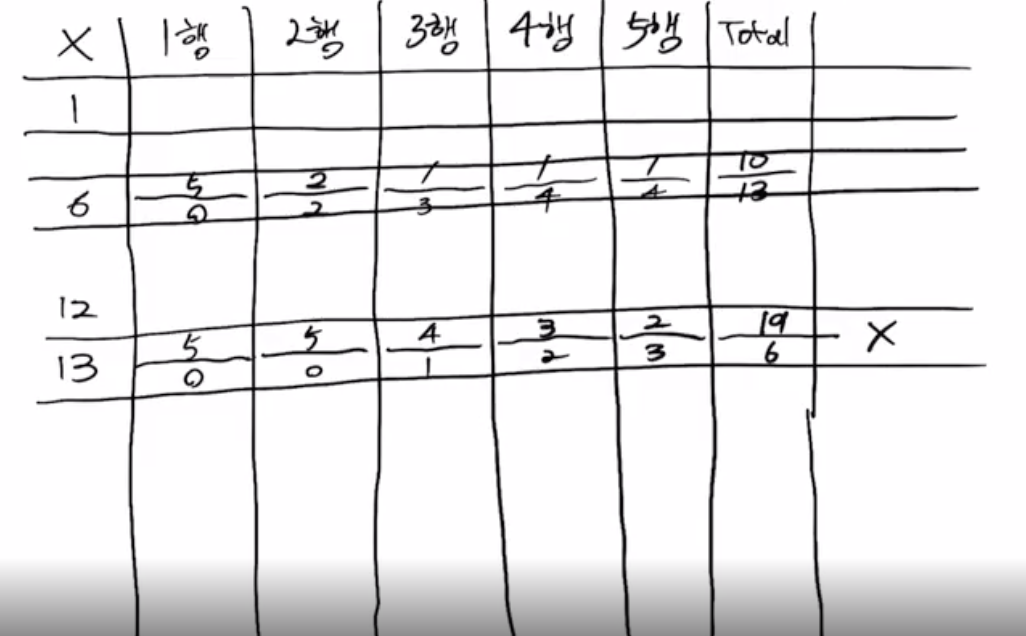
x는 1(low)부터 25(high)까지이고 midpoint를 찾으면서 위 조건을 만족시키는 값을 찾아낸다. 여기서 핵심은 get_num_smaller과 get_num_bigger 함수를 어떻게 구현해낼 것인가에 관한 것이었는데 아래 코드를 보자.

# 문제에서 주어진 nxn 이차원 배열에서 x보다 작은 수의 개수를 구하여 반환하는 함수
def get_num_smaller(x: int) -> int:
    num_smaller = 0
    for i in range(1, n+1):
        # i번째 행에서 x보다 작은 수의 개수는 min(n, (x-1)//i)
        num_smaller += min(n, (x-1)//i)
    return num_smaller

다른 부분은 다 이해가 갔는데 num_smaller += min(n,(x-1) // i) 이 부분이 처음에는 이해가 가지 않았다. i번째 행, j번째 열을 곱한 값, 즉 ixj < x를 만족시켜야 하는데 이를 다시 정리해보면 j < x // i가 된다. 만약 num_smaller += min(n,x // i)를 써 놓는다면, x가 12이고 i가 3일 때 j가 4이므로 num_smaller값은 4가 되는데 x보다 작은 수의 개수를 구해야 하기 때문에 (x-1) // i를 써놓아야 한다. min을 써놓은 이유는 각각의 row를 돌 때 n을 넘으면 안되기 때문이다.

def get_num_bigger(x: int) -> int:
    num_bigger = 0
    for i in range(1, n+1):
        # i번째 행에서 x보다 큰 수의 개수는 n-min(n, x//i)
        num_bigger += n - min(n, x//i)
    return num_bigger

get_num_bigger을 구할 때도 패턴은 비슷하되 이번에는 n-(i번째 항에서 x보다 작거나 같은 수의 개수)를 해야 하기 때문에 '같은'이 포함된 경우 x // i가 되고 n-min(n,x // i)가 되는 것이다.