[Algorithm] BAEKJOON 17103 - 골드바흐 파티션 C++

[BAEKJOON] 17103번 골드바흐 파티션

문제 골드바흐의 추측: 2보다 큰 짝수는 두 소수의 합으로 나타낼 수 있다.
짝수 N을 두 소수의 합으로 나타내는 표현을 골드바흐 파티션이라고 한다. 짝수 N이 주어졌을 때, 골드바흐 파티션의 개수를 구해보자. 두 소수의 순서만 다른 것은 같은 파티션이다.

입력 첫째 줄에 테스트 케이스의 개수 T (1 ≤ T ≤ 100)가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 N은 짝수이고, 2 < N ≤ 1,000,000을 만족한다.

출력 각각의 테스트 케이스마다 골드바흐 파티션의 수를 출력한다.

Input

5 6 8 10 12 100

Output

1 1 2 1 6

Code

#include <iostream>

using namespace std;


int main(){
    ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
	
    int num, N;
    cin >> num;

    bool arr[1000001] = {false, };
    arr[0]=arr[1]=true;

    for(int i=2; i*i<1000001; i++){
        if(arr[i]) continue;
        for(int j=2*i; j<1000001; j+=i) arr[j] = true;
    }
 
    while(num--){
        cin >> N;
        int count=0;

        for(int i=2; i<=N/2; i++) if(!arr[i] && !arr[N-i]) count++;
        cout << count << '\n';
    }

    return 0;
}

---

풀이

골트바흐의 추측에 따르면, 2보다 큰 모든 짝수는 두개의 소수(Prime nember)의 합으로 표시할 수 있다. 하나의 소수를 두 번 사용하는 것 또한 허용된다. 이를 기반으로 2보다 큰 짝수에 대한 소수를 중복을 허용하고 쭉 나열해 본다면 아래와 같다.

짝수	골트바흐 파티션
4	2+2
6	3+3
8	3+5 = 5+3
10	3+7 = 5+5 = 7+3
...	...
22	3+19 = 5+17 = 11+11 = 17+5 = 19+3

표를 들여다보면 숫자들 사이에서 어떤 규칙을 발견할 수 있다. 바로 하나의 소수의 합으로 이루지거나 중간을 기점으로 대칭하다는 것 이다.

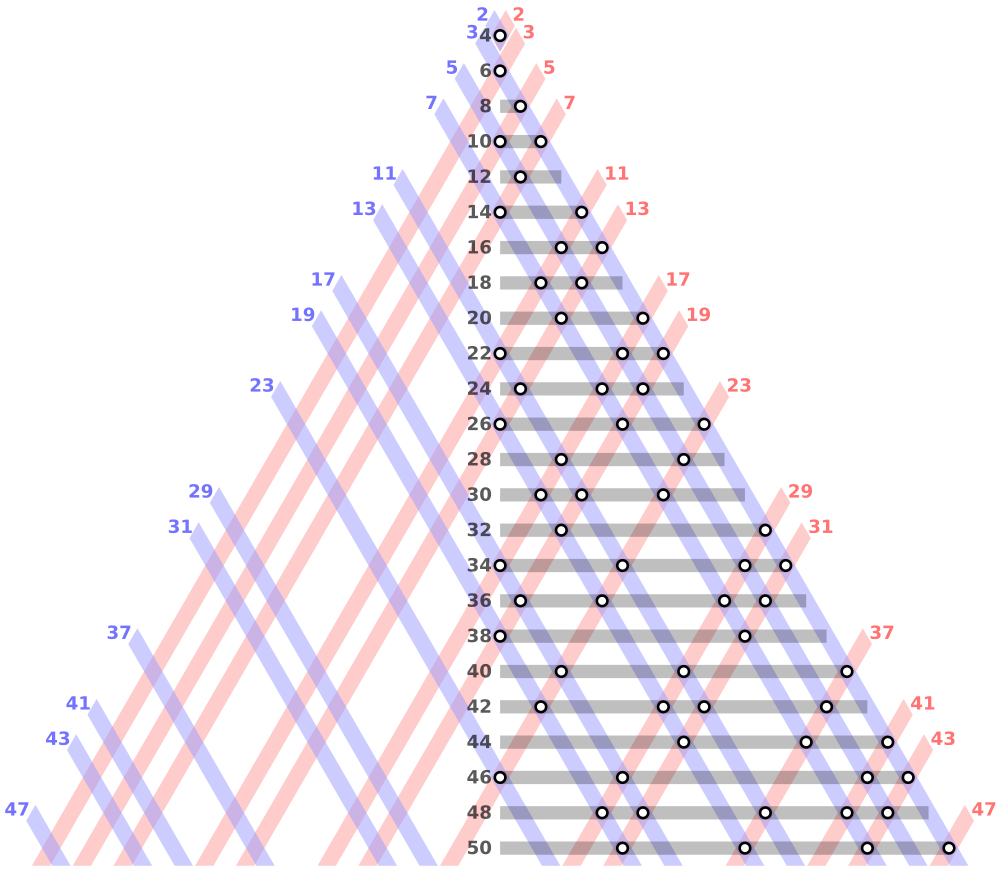
출처 : [wikipedia] 골트바흐의 추측

이 이미지는 골트바흐의 숫자를 짝수 50까지 시각화한 것이며, 대칭한 규칙을 쉽게 확인할 수 있다. 이 대칭성을 토대로 임의의 짝수 N의 골트바흐 파티션은 임의의 소수 a가 있을 때 N-a가 소수면 그 조건이 성립된다. 이 조건을 만족하는 소수 a의 개수를 구하면 골트바흐 파티션의 개수를 구할 수 있다.

이때, 소수 a는 골트바흐 숫자의 대칭성에 따라 N의 절반 이하의 범위에서 찾을 수 있다. 코드로는 2부터 주어진 임의의 짝수/2 까지의 반복 내에서 위 조건을 만족하는 소수 쌍의 개수를 구하는 방향으로 작성할 수 있다.

---

시행착오

처음에 호기롭게 작성한 식에서 N/2까지 유추를 했지만 시간복잡도가 O(N)이어서 시간 초과를 맛봤다. 이번 기회에 시간복잡도를 고려하면서 더 좋은 코드를 구현할 수 있도록 고민하는 과정의 필요성을 몸소 느꼈다.

#include <iostream>

using namespace std;


int main(){
    ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
	
    int num, N;
    cin >> num;

    bool arr[1000001] = {false, };
    arr[0]=arr[1]=true;

    for(int i=2; i*i<1000001; i++){
        if(arr[i]) continue;
        for(int j=2*i; j<1000001; j+=i) arr[j] = true;
    }
 
    while(num--){
        cin >> N;
        int count=0;

        for(int i=2; i<=N/2; i++){
            for(int j=N-1; j>=N/2; j--){
                if(!arr[i] && !arr[j]){
                    if(i+j<N) break;
                    else if(i+j == N)
                        count++;
                }
                else continue;
            }
        }

        cout << count << '\n';
    }

    return 0;
}