[Paper Review] 3D Gaussian Splatting for Real-Time Radiance Field Rendering

E0u0n·2024년 2월 16일

3D Gaussian Splatting

목록 보기

1/1

Paper : 3D Gaussian Splatting for Real-Time Radiance Field Rendering

Abstract

배경

Radiance Field 방법은 높은 시각적 품질을 달성하기 위해서 여전히 훈련 및 렌더링에 비용이 많이 드는 신경망이 필요

최근의 더 빠른 방법은 필연적으로 품질과 속도를 절충

(고립된 객체가 아닌) 무한하고 완전한 장면과 1080p 해상도 렌더링의 경우 현재 어떤 방법으로도 실시간 표시 속도를 달성할 수 없음

제안

경쟁력 있는 훈련 시간을 유지하면서 최첨단 시각적 품질을 달성할 수 있게 하고 중요한 것은 1080p 해상도에서 고품질 실시간(≥ 30fps) 새로운 뷰 합성을 허용하는 세 가지 핵심 요소

카메라 보정 중에 생성된 희소 점부터 시작하여 빈 공간에서 불필요한 계산을 피하면서 장면 최적화를 위한 연속 체적 복사 필드의 바람직한 속성을 보존하는 3D 가우시안으로 장면을 표현

3D 가우시안의 인터리브 최적화/밀도 제어를 수행하며, 특히 장면의 정확한 표현을 달성하기 위해 이방성 공분산을 최적화

이방성 스플래팅을 지원하고 훈련을 가속화하며 실시간 렌더링을 허용하는 빠른 가시성 인식 렌더링 알고리즘을 개발

결과

여러 확립된 데이터 세트에서 최첨단 시각적 품질과 실시간 렌더링을 시연

1. INTRODUCTION

3. OVERVIEW

Sec.4 : 본 연구의 입력은 정적인 장면의 이미지 세트와 함께, SfM에 의해 calibration된 해당 카메라로, 이는 부수적으로 sparse point cloud를 생성한다. 이 점들로부터 위치(평균), 공분산 행렬 및 불투명도 $\alpha$ 로 정의되는 3D Gaussian들을 생성한다. 이는 매우 유연한 최적화 체제를 가능하게 한다. 이는 세부 구조를 compact하게 표현할 수 있는 부분적으로 강한 anisotropic(비등방성) volumetric splats을 사용하기 때문에, 3D 장면을 합리적으로 compact하게 표현할 수 있다.
Radiance field의 색상은 기존 연구(plenoxels, instant-ngp)에 따라 spherical harmonics(SH)로 표현한다.

Sec.5 : 본 연구의 알고리즘은 Gaussian density의 적응적 제어를 위한 연산과 3D Gaussian parameters(interleaved position, covariance, $\alpha$ , SH coefficients)의 최적화를 통해 radiance field representation을 생성한다.

Sec.6 : 본 연구가 효율적일 수 있었던 것은 tile-based rasterizer로, 빠른 정렬을 통해 가시성 순서를 존중하여 anisotropic splat를 $\alpha$ -블렌딩할 수 있다. 빠른 rasterizer는 또한 누적된 $\alpha$ 값을 추적함으로써, gradient를 받을 수 있는 Gaussian의 수에 제한 없이 빠른 backward pass를 포함한다.

4. DIFFERENTIABLE 3D GAUSSIAN SPLATTING

본 연구는 방향성이 없는 sparse (SfM) 점 세트로부터 scene representation을 최적화하여 고품질의 새로운 뷰를 합성하는 것을 목표로 한다. 이를 위해서는 미분 가능한 volumetric representation의 속성을 상속하면서 빠른 렌더링이 가능하도록 비구조적이고 명시적인 primitive가 필요하다. 본 연구는 미분 가능하고 2D splat으로 쉽게 투영할 수 있는 3D Gaussian를 선택하여 렌더링을 위한 빠른 $\alpha$ -블렌딩을 사용한다.

3D Gaussian
3차원 공간에서의 가우스 함수(Gaussian function)를 의미하며, 3차원 가우시안 분포는 중심(평균) $μ$ 와 공분산 행렬 $Σ$ 에 의해 정의된다. 중심은 3D 공간에서 분포의 위치를 나타내며, 공분산 행렬은 분포의 형태와 방향성을 결정된다. 아래 함수는 공간에서의 어떤 점 $\mathbf x$ 가 주어진 평균 $μ$ 와 공분산 $Σ$ 를 가진 3차원 정규 분포에 속할 확률 밀도를 계산한다. 공분산 행렬은 분포가 얼마나 퍼져 있는지(변동성), 그리고 분포의 주축이 어떤 방향을 가리키는지를 나타낸다.
$f(\mathbf{x}) = \frac{1}{(2\pi)^{\frac{3}{2}}|\Sigma|^{\frac{1}{2}}} \exp\left(-\frac{1}{2}(\mathbf{x}-\mu)^T\Sigma^{-1}(\mathbf{x}-\mu)\right)$

$\mathbf x$ : 3차원 공간의 점을 나타내는 벡터

$μ$ : 분포의 평균을 나타내는 3차원 벡터

$Σ$ : 3x3 공분산 행렬로, 분포의 형태와 방향을 결정

$∣Σ∣$ : $Σ$ 의 행렬

700만 개의 Gaussian 으로 이루어진 scene representation

완전 불투명하게 레스터화된 Gaussian

https://huggingface.co/blog/gaussian-splatting

법선을 가진 작은 평면 원인 2D 점들을 사용하여 장면을 표현하는 기존 연구들이 활발히 진행되었다. 그러나 본 연구에서 사용하는 SfM 점은 희소하게 분포되어 있으며, 충분히 밀집되어 있지 않은 점들은 이웃하는 점들 사이의 관계를 기반으로 법선을 추정하기 매우 어려워 각 점의 정확한 방향을 나타내는 법선 벡터를 정확하게 추정하기 어렵다. 이에 본 연구는 법선이 필요하지 않은 3D Gaussian 세트로 geometry를 모델링한다. Gaussian은 world space에서 정의된 전체 3D 공분산 행렬 $Σ$ 에 의해 정의되며, 점(평균) $\mu$ 를 중심으로 한다. 이 Gaussian은 블렌딩 과정에서 $\alpha$ 로 곱해진다:

G(x) = e^{-\frac{1}{2} x^T \Sigma^{-1} x} \tag 4

3D Gaussian을 2차원으로 투영하기 위한 Viewing transformation $𝑊$ 가 주어지면 카메라 좌표의 공분산 행렬 $Σ^′$ 은 다음과 같다:

\Sigma' = J W \Sigma W^T J^T\ \tag 5

$𝐽$ : projective transformation의 affine approximation의 Jacobian
만약 $Σ^′$ 의 세 번째 행과 열을 생략한다면, 이전 연구에서 법선을 가진 평면 점들로부터 시작했을 때와 동일한 구조와 속성을 가진 2×2 분산 행렬을 얻을 수 있음

Radiance field를 나타내는 3D Gaussian을 얻기 위한 직접적인 접근 방식은 공분산 행렬 $Σ$ 를 직접 최적화하는 것이다. 그러나 공분산 행렬은 양의 준정부호일 때만 물리적 의미를 가진다.

양의 준정부호 공분산 행렬
양의 준정부호 공분산 행렬은 관찰하고 분석하려는 현상이나 데이터가 '실제로 가능하고, 물리적으로 타당하며, 계산할 수 있음'을 의미한다. 이는 양의 준정부호 행렬이 갖는 특성 때문이다.

긍정적인 변동성: 공분산 행렬에서 변수들의 변동성(분산)은 항상 양수여야 한다. 실제 세계에서는 어떤 것의 변화량이 '음수'가 될 수 없기 때문이다.

현실적인 관계: 변수들 사이의 관계(공분산)도 현실적이어야 한다. 양의 준정부호 공분산 행렬은 이 관계가 실제 세계의 관측 가능한 현상을 반영한다는 것을 보장한다.

계산 가능성: 양의 준정부호 행렬은 계산상 필요한 여러 조건(예: 역행렬 존재)을 만족시킨다.

파라미터 최적화를 위한 gradient descent의 사용은 공분산 행렬을 항상 양의 준정부호(유효하게)로 유지하는 것이 어렵다. 이는 gradient descent 혹은 업데이트 단계에서 공분산 행렬의 고유값이 음수가 되는 것처럼 양의 준정부호를 깨트릴 가능성이 있기 때문이다.

따라서 본 연구에서는 더 직관적이면서도 표현력이 동등한 방법으로 최적화를 진행한다. 3D Gaussian의 공분산 행렬 $Σ$ 는 타원체의 형태와 유사하다는 특징을 통해, 복잡한 수학적 제약을 직접 다루는 대신, 타원체의 형태를 조정하여 3D 공간에서 객체를 모델링하는 방식을 선택했다. 타원체의 크기와 방향은 스케일링 행렬 $𝑆$ 와 회전 행렬 $𝑅$ 로 정의되며, 이 두 행렬을 사용하여 해당하는 공분산 행렬 $Σ$ 을 찾을 수 있다:

\Sigma = R S S^T R^T \tag 6

본 연구는 두 요소를 분리하여 저장하는 방식을 사용하며, 스케일링을 위한 3D 벡터 $𝑠$ 와 회전을 나타내는 쿼터니언 $𝑞$ 을 별도로 다룬다. 이러한 분리 저장 방식은 각 요소를 쉽게 최적화하고, 필요할 때 해당하는 행렬로 변환하여 결합할 수 있게 해준다. 이때, 쿼터니언 $𝑞$ 는 유효한 단위 쿼터니언(unit quaternion)을 얻기 위해 정규화한다.

훈련 중 자동 미분으로 인한 상당한 오버헤드를 피하기 위해 모든 매개변수에 대한 gradient를 명시적으로 유도한다. 즉, 훈련 과정을 최적화하고 계산 효율성을 높이기 위해 gradient 계산을 수동으로 수행한다. 이런 표현 방식은 anisotropic covariance을 최적화하는 데 적합하며, 캡처된 장면의 다양한 형태의 geometry에 맞게 3D Gaussian을 조정할 수 있게 한다. 이로 인해 상대적으로 컴팩트한 표현이 가능해지며, 이는 다양한 형태를 효율적으로 모델링할 수 있음을 의미한다.

5. OPTIMIZATION WITH ADAPTIVE DENSITY CONTROL OF 3D GAUSSIANS

위치 $𝑝$ , $\alpha$ , 공분산 $Σ$ , 각 가우시안의 색상 $𝑐$ 를 나타내는 SH 계수를 최적화하여 장면의 view-dependent 색상 정확히 포착한다. 이 최적화 과정은 장면을 더 잘 표현하기 위해 Gaussian density를 제어하는 단계와 교차하여 진행된다.

5.1. Optimization

3D에서 2D로 투영하는 과정에서 투영의 모호성으로 인해 geometry가 잘못 배치될 수 있기에, 최적화 과정은 geometry를 생성하고, 잘못 배치된 경우 이를 파괴하거나 이동할 수 있도록 한다. 또한, 3D Gaussian의 공분산 파라미터(형태와 방향)를 정확하게 조절하는 것은 전체 장면을 간결하게 표현하는 데 중요한 역할을 한다. 본 연구는 이를 바탕으로 아래의 스펙으로 최적화를 진행한다.

SGD(Stochastic Gradient Descent) 사용
표준 GPU 가속 프레임워크 및 일부 연산에 대해 사용자 정의 CUDA 커널 추가
Fast rasterization(Sec.6)를 통해 레스터화 과정의 최적화 효율을 높임
activation function
- sigmoid activation function : 투명도 𝛼 를 $[0, 1)$ 범위로 제한하고 부드러운 Gradient를 얻기 위해
- exponential activation function : 공분산의 스케일에 대해
초기 공분산 행렬 추정 : 가장 가까운 세 점까지의 거리 평균을 이용하여 등방성(Isotropic) 가우시안의 축을 설정한다.

isotropic Gaussian
모든 방향으로 동일한 스케일을 가진 가우시안을 의미하며, 이 경우에는 모든 방향으로 확산되는 정도가 동일하다고 가정한다.
위치 최적화 : "Plenoxels"에 소개된 것과 유사한 표준 exponential decay scheduling 기법을 사용하지만, 이는 위치 파라미터에만 적용한다.

exponential decay scheduling
파라미터가 시간이 지남에 따라 서서히 감소하도록 조정하는 방법으로, 최적화 과정에서 파라미터 값의 변화를 안정적으로 만들어 준다.
loss function : L1과 D-SSIM 항을 결합한다: $\mathcal{L} = (1 - \lambda)\mathcal{L}_1 + \lambda\mathcal{L}_{D-SSIM} \tag 7$

5.2. Adaptive Control of Gaussians

SfM에서 얻은 초기 sparse 점들로부터 장면을 더 잘 표현하기 위해 가우시안의 수와 밀도를 적응적으로 제어하는 방법을 적용한다. 이 과정은 처음에는 희소한(sparse) 가우시안 세트에서 시작하여, 최적화를 거쳐 더 조밀한(denser) 가우시안 세트로 전환함으로써, 장면을 더 정확하게 표현하고 올바른 파라미터를 가질 수 있다.

최적화 초기 단계 (Sec.7) 후, 100번의 반복마다 가우시안을 밀집시키고 투명한( $\alpha$ 가 임계값 $\epsilon_{\alpha}$ 보다 작은) 가우시안을 제거한다. 이 적응적 제어를 통해 빈 공간을 채우며, 주로 기하학적 특징이 누락된 영역("재구성 미달")과 가우시안이 장면에서 큰 영역을 커버하는 영역("재구성 과다")에 집중한다. 이러한 영역은 대개 시각 공간에서 큰 위치 변화(gradient)를 가진다. 직관적으로, 이는 아직 잘 재구성되지 않은 영역에 해당하며, 최적화 과정은 이 가우시안을 이동시켜 이를 수정하려고 시도한다.

두 경우 모두 조밀화(densification)에 좋은 후보이므로, 이런 영역에서 가우시안을 조밀하게 만들기 위해, 시각 공간 위치 변화(gradient)의 평균 크기가 임계값 $\tau_\text{pos}$ (실험에서는 0.0002) 이상인 가우시안을 선별하여 조밀화한다.

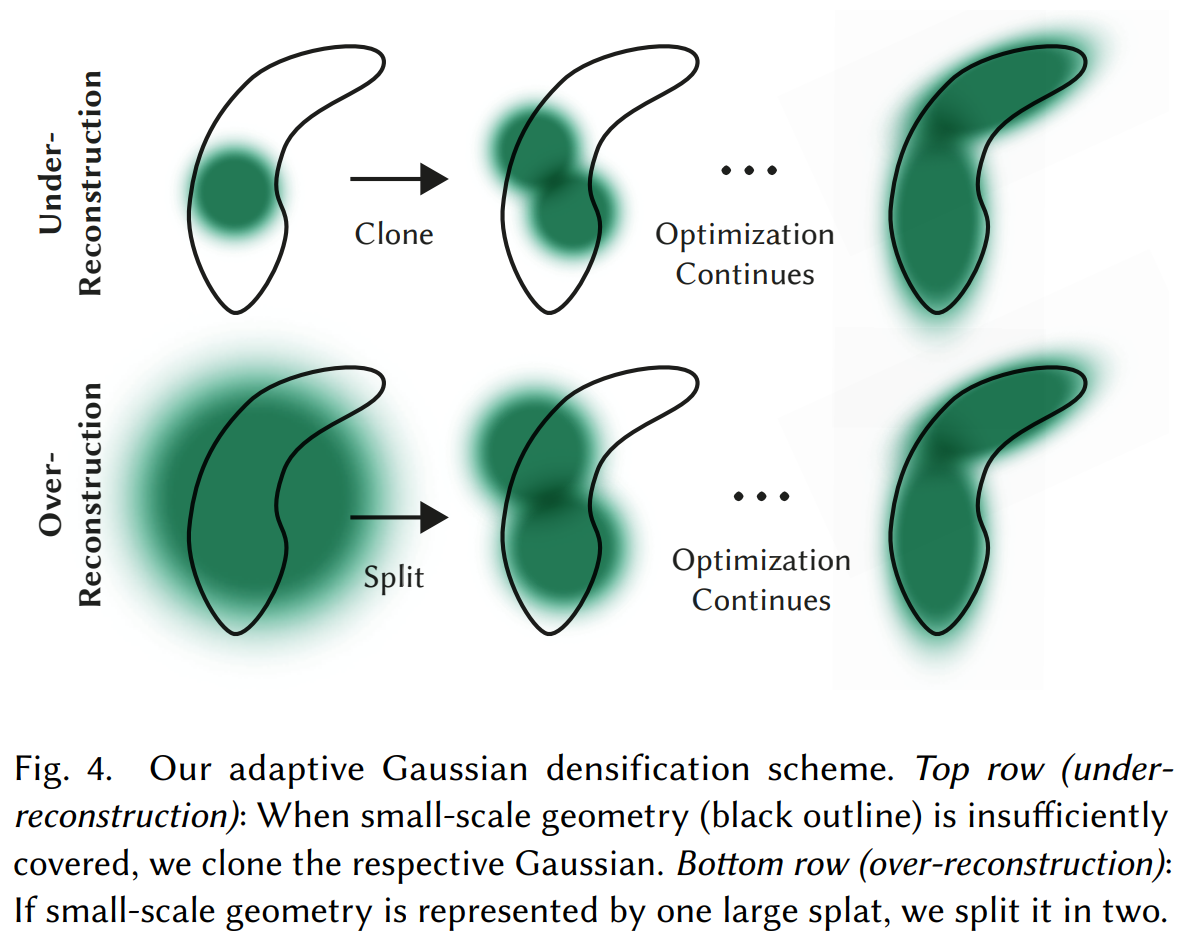
재구성이 덜 된 영역에 있는 작은 가우시안의 경우, 새로 생성되어야 geometry를 커버하기 위해 가우시안을 복제하는 방법을 사용할 수 있다. 이는 동일한 크기의 복사본을 생성하고, 위치 변화의 방향으로 이동시키는 것을 의미한다. 반면에, 변동성이 높은 영역에 있는 큰 가우시안은 더 작은 가우시안으로 분할해야 한다. 이 과정에서 큰 가우시안을 두 개의 새로운 가우시안으로 대체하고, 그들의 스케일을 실험적으로 결정된 비율인 $\phi = 1.6$ 으로 나눈다. 또한, 새로운 가우시안의 위치를 초기화하기 위해 원본 3D 가우시안을 확률 밀도 함수(PDF)로 사용하여 샘플링한다.

가우시안의 처리 방식은 1) 시스템의 총 부피와 가우시안 수를 모두 증가시키는 상황을 감지하고 처리하거나, 2) 총 부피는 유지하되 가우시안의 수를 증가시키는 방식이 있다. 다른 volumetric representation 방법들과 마찬가지로, 최적화 과정은 입력 카메라 근처에 부유물(floaters)이 존재하면 이 부분에 너무 많은 가우시안을 할당하게 되어 때문에 문제가 발생할 수 있다. 이는 실제보다 더 많은 디테일을 추가할 수 있으며, 결과적으로 가우시안 밀도의 불필요한 증가로 이어질 수 있다. 이런 경우, 가우시안의 수 증가를 조절하는 효과적인 방법은 매 $N=3000$ 반복마다 $\alpha$ 값을 거의 0으로 설정하는 것이다. 이를 통해, 최적화 과정에서 필요한 곳에 가우시안의 $\alpha$ 를 증가시키면서, $\epsilon_{\alpha}$ 보다 작은 가우시안을 제거할 수 있다.

가우시안은 축소되거나 확장되어 다른 가우시안과 겹칠 수 있기에, 주기적으로 world space에서 크거나 view space에서 큰 영역을 가진 가우시안을 제거한다. 이 전략은 가우시안의 총 수를 잘 제어할 수 있게 한다. 본 연구의 모델에서 가우시안은 항상 유클리드 공간에서 primitives로 남아 있기 때문에, 다른 연구에서 필요로 하는 공간 압축, 왜곡, 먼 거리나 큰 가우시안에 대한 투영 전략을 사용하지 않는다.

6. FAST DIFFERENTIABLE RASTERIZER FOR GAUSSIANS

본 연구는 고속 렌더링과 정렬을 정렬을 달성하기 위한 새로운 tile-based rasterizer 설계에 초점을 맞춘다. 목표는 anisotropic splats를 포함하여 $\alpha$ -블렌딩을 위한 근사적 처리를 가능하게 하는 것으로, 이는 이전 연구에서 발견된 gradient를 받을 수 있는 스플랫의 수에 대한 제한을 극복하기 위함이다.

이 접근 방식은 최근의 소프트웨어 래스터화 기술(Pulsar)에서 영감을 받았으며, 전체 이미지에 대해 한 번에 primitive를 사전 정렬함으로써 픽셀 당 발생하는 정렬 비용을 줄인다. 이 fast rasterizer는 낮은 추가 메모리 소비와 픽셀 당 일정한 오버헤드만을 요구하면서, 혼합된 가우시안에 대한 효율적인 역전파를 가능하게 한다. 더욱이, 이 파이프라인은 완전히 미분 가능하며, 2D로의 투영(Sec.4)을 고려할 때 이전의 2D splatting 방법과 유사하게 anisotropic splat을 rasterize할 수 있다.

구현 과정과 세부 사항

화면 분할과 3D Gaussians의 culling : 화면은 16×16 타일로 분할되고, 3D Gaussians는 view frustum 및 각 타일에 대해 제외(culling) 과정을 거친다. 구체적으로, view frustum과 99% 신뢰 구간이 겹치는 Gaussians 만이 유지된다. 또한, 극단적 위치에 있는 Gaussians(평균이 near 평면에 가깝고 view frustum 바깥쪽에 있는 경우)을 쉽게 제외하기 위해 guard band를 사용한다.
가우시안의 인스턴스화 : 각 Gaussian은 겹치는 타일의 수에 따라 인스턴스화되며, 각 인스턴스에는 view space 깊이와 타일 ID를 결합한 key가 할당된다.
정렬 메커니즘 : 이 key를 기반으로 한 빠른 GPU Radix 정렬을 사용하여 Gaussian을 정렬한다. 중요한 점은, 추가적인 픽셀별 정렬 없이 이 초기 정렬을 기반으로 블렌딩이 수행된다는 것이다.
$\alpha$ -블렌딩 : $\alpha$ -블렌딩은 일부 설정에서 특정 설정에서는 근사치일 수 있으나, splat 크기가 개별 픽셀 크기에 접근함에 따라 이 근사치의 영향은 무시할 수 있게 된다. 이러한 선택이 훈련 및 렌더링 성능을 크게 향상시키며, 최종적으로 수렴된 장면에서 눈에 띄는 artifact가 없는 결과를 제공한다.

타일 기반 가우시안 스플랫 래스터화

가우시안 정렬 : 전체 렌더링 과정에서 처리할 가우시안들을 깊이에 따라 정렬한다. 이 정렬 과정을 통해 각 타일에서 처리할 첫 번째와 마지막 가우시안을 식별하고, 이에 대한 정보를 리스트로 만든다.
스레드 블록 실행 : rasterization을 위해, 각 타일에 대하여 독립적인 스레드 블록을 할당하고 실행한다. 이는 타일마다 고유한 렌더링 작업을 병렬로 수행할 수 있게 한다.
공유 메모리를 통한 데이터 로드 : 각 스레드 블록은 협업적으로 공유 메모리에 가우시안 패킷을 로드한다.
색상과 투명도 누적 : 주어진 픽셀에 대해, 앞에서 뒤로 리스트를 순회하며 색상과 α 값을 누적한다. 이는 데이터 로딩/공유와 처리의 병렬성을 최대화한다.
투명도 포화 조건과 타일 처리 종료 : 픽셀의 투명도 값이 포화 상태(즉, $\alpha = 1$ )에 도달하면, 해당 스레드는 처리를 중단한다. 이는 불필요한 계산을 줄이고 렌더링 효율을 높인다. 또한, 타일 내 모든 픽셀이 포화 상태에 도달하면, 해당 타일의 처리가 종료된다.

렌더링 최적화와 혁신적 접근 방식

$\alpha$ 포화 조기 중단 기준 : rasterization 중, 픽셀의 투명도 $\alpha$ 값이 특정 포화 상태(예: $\alpha==1$ )에 도달하면 해당 픽셀의 처리를 즉시 중단한다. 이 전략은 불필요한 계산을 방지하고 전체 렌더링 시간을 단축시킨다.
제한 없는 gradient 업데이트 : 이 접근법은 gradient 업데이트를 받는 혼합된 primitive의 수에 제한을 두지 않는다. 이를 통해 임의의 깊이 복잡성을 가진 장면을 더 정확하게 처리할 수 있으며, 넓은 범위의 장면에 대해 하이퍼파라미터 조정 없이도 효과적인 렌더링이 가능하다.
backward pass에서의 점 복구 : forward pass에서 혼합된 점들의 순서를 backward pass 동안 효율적으로 복구해야 한디. 이 과정은 동적 메모리 관리의 오버헤드를 최소화하기 위해 타일별로 점들의 리스트를 재순회하는 방식으로 진행된다. 이때 forward pass에서 사용된 가우시안 배열과 타일 범위를 재사용할 수 있다.
gradient 계산 용이화: backward pass에서는 가우시안과 타일 범위를 뒤에서 앞으로 순회하며, 필요한 gradient 정보를 효율적으로 수집한다. 이 방법은 gradient 계산을 용이하게 하며, 전체적인 렌더링 프로세스의 효율을 높인다.

고급 렌더링 최적화 기법

점들의 역방향 순회 : 렌더링 과정에서, 특정 타일 내의 픽셀들에 영향을 미친 마지막 점부터 시작하여 점들을 역순으로 순회한다. 이 점들은 공유 메모리를 통해 효율적으로 다시 로드되어, backward pass에서 처리된다.
중첩 검사와 점 처리 : 각 픽셀은 순방향 패스에서 해당 색상에 기여한 마지막 점이 가진 깊이보다 낮거나 같은 깊이를 가진 점들에 대해서만 중첩 검사(overlap testing)와 처리를 진행한다. 이 과정은 렌더링에서 불필요한 계산을 줄이는 데 중요한 역할을 한다.
불투명도 값의 복구 : gradient 계산을 위해서는 forward pass에서 누적된 불투명도 값이 필요하다. backward pass에서는 forward pass 끝에서의 총 누적 불투명도를 기반으로, 각 점의 불투명도를 나누어 gradient 계산에 필요한 계수를 얻는다. 이 방식은 불투명도 값의 복구를 용이하게 하여, gradient 계산의 정확도를 향상시킨다.

7. IMPLEMENTATION, RESULTS AND EVALUATION

7.1. Implementation

7.2. Results and Evaluation

7.3. Ablations

7.4. Limitations

E0u0n

이세계 개발자입니다.