[알고리즘 문제풀이] 프로그래머스 다리를 지나는 트럭

프로그래머스 고득점 kit의 스택/큐 분류에 있는 level2 문제를 풀어보았습니다 ! 순서대로 풀고 있었고, 스택/큐 분류는 한 문제가 남았었는데, 아무래도 새로 추가된 문제인 것 같다 !
https://programmers.co.kr/learn/courses/30/lessons/42583

문제 설명

트럭 여러 대가 강을 가로지르는 일 차선 다리를 정해진 순으로 건너려 합니다. 모든 트럭이 다리를 건너려면 최소 몇 초가 걸리는지 알아내야 합니다. 트럭은 1초에 1만큼 움직이며, 다리 길이는 bridge_length이고 다리는 무게 weight까지 견딥니다.
※ 트럭이 다리에 완전히 오르지 않은 경우, 이 트럭의 무게는 고려하지 않습니다.

예를 들어, 길이가 2이고 10kg 무게를 견디는 다리가 있습니다. 무게가 [7, 4, 5, 6]kg인 트럭이 순서대로 최단 시간 안에 다리를 건너려면 다음과 같이 건너야 합니다.

경과 시간	다리를 지난 트럭	다리를 건너는 트럭	대기 트럭
0	[]	[]	[7,4,5,6]
1~2	[]	[7]	[4,5,6]
3	[7]	[4]	[5,6]
4	[7]	[4,5]	[6]
5	[7,4]	[5]	[6]
6~7	[7,4,5]	[6]	[]
8	[7,4,5,6]	[]	[]

따라서, 모든 트럭이 다리를 지나려면 최소 8초가 걸립니다.

solution 함수의 매개변수로 다리 길이 bridge_length, 다리가 견딜 수 있는 무게 weight, 트럭별 무게 truck_weights가 주어집니다. 이때 모든 트럭이 다리를 건너려면 최소 몇 초가 걸리는지 return 하도록 solution 함수를 완성하세요.

제한 조건

• bridge_length는 1 이상 10,000 이하입니다.
• weight는 1 이상 10,000 이하입니다.
• truck_weights의 길이는 1 이상 10,000 이하입니다.
• 모든 트럭의 무게는 1 이상 weight 이하입니다.

입출력 예

bridge_length	weight	truck_weights	return
2	10	[7,4,5,6]	8
100	100	[10]	101
100	100	[10,10,10,10,10,10,10,10,10,10]	110

풀이 방법

시간이 1씩 지남에 따라서 트럭들을 하나씩 다리 위로 위치 시킨다. 이 때, 다리 위의 무게를 저장해주고, 이 값을 이용하여 트럭이 더 올라올 수 있는지 체크하고 트럭이 더 올라올 수 있는지 아닌지 판별한다. 후에 다리 위에 올라와있는 트럭들을 1씩 이동시키고, 다 이동한 트럭은 다리에서 내려오게끔 처리해준다.

트럭의 무게와 다리 위에 있던 시간을 담는 Truck 클래스를 정의하여 사용하였다. 또한 이 Truck 클래스를 담는 자료구조를 이용하여 다리 위에 있는 트럭들을 담아주었다. 트럭이 이 자료구조에 담기고, 빠질 때 현재 다리위의 무게를 담고있는 변수를 업데이트 해주었다. 대기중인 트럭이 다 사라지면 for 문이 종료되게 코드를 작성하였기 때문에 다리 위에 남아있는 트럭 중 가장 마지막에 올라온 트럭이 다리를 빠져나오면 종료되는 것이므로 마지막에 올라온 트럭의 남은 시간을 더해주어 최종 값을 구하였다.

+) 지금 작성하며 생각난 것인데, 만약 다리 위에 더이상 트럭이 올라올 수 없는 경우 1씩 시간을 지나게 하는 것이 아닌 제일 앞에 있는 트럭의 남은 시간을 한 번에 더해준다면 더 짧은 시간에 결과 값을 구할 수 있을 것이다.

+) 코드로 보면 이동하는 거리를 담는 변수를 따로 선언해두고, 트럭이 더 올라올 수 있는지 판별하는 if문에서 if에 들어가면 1을 할당, else라면 맨 앞에 있는 트럭의 남은 시간을 할당하여 주고, for문에서 이동시키는 것을 기존에 time++로 했던 것을 time+이동거리로 변경해주고, 시간을 의미하는 answer도 answer++이 아닌 answer+이동거리로 변경하면 될 것 같다 !

+) ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ 이렇게 글로만 쓸게 아니라 한두줄인데 걍 고치자 해서 고쳤다 !

코드(Queue 사용)

import java.util.LinkedList;
import java.util.Queue;

public class Solution {

    public static class Truck{
        int weight;
        int time;
        Truck(int weight){
            this.weight = weight;
            this.time = 0;
        }
    }

    public static int solution(int bridge_length, int weight, int[] truck_weights) {
        int answer = 1;
        int current = 0;
        Queue<Truck> onBridge = new LinkedList<>();
        for (int i=0; i<truck_weights.length; i++) {
            if (onBridge.isEmpty() || current+truck_weights[i] <= weight){
                onBridge.add(new Truck(truck_weights[i]));
                current += truck_weights[i];
            }
            else i--;
            for(Truck truck : onBridge){
                truck.time++;
            }
            while(!onBridge.isEmpty() && onBridge.peek().time == bridge_length){
                current -= onBridge.peek().weight;
                onBridge.poll();
            }
            answer++;
        }
        while (onBridge.size() > 1) onBridge.poll();
        return answer+(bridge_length - onBridge.peek().time);
    }
}

코드(Vector 사용)

import java.util.Vector;

public class Solution {
    public static class Truck{
        int weight;
        int time;
        Truck(int weight){
            this.weight = weight;
            this.time = 0;
        }
    }

    public static int solution(int bridge_length, int weight, int[] truck_weights) {
        int answer = 1;
        int current = 0;
        Vector<Truck> onBridge = new Vector<>();
        for (int i=0; i<truck_weights.length; i++) {
            if (onBridge.isEmpty() || current + truck_weights[i] <= weight){
                onBridge.add(new Truck(truck_weights[i]));
                current += truck_weights[i];
            }
            else i--;
            for (int j = 0; j < onBridge.size() ; j++) {
                onBridge.get(j).time++;
                if (onBridge.get(j).time == bridge_length){
                    current -= onBridge.get(j).weight;
                    onBridge.remove(j);
                    j--;
                }
            }
            answer++;
        }
        return answer+(bridge_length - onBridge.get(onBridge.size()-1).time);
    }
}

코드 (Vector + 이동거리 변수 사용)

import java.util.Vector;

public class Solution {
    public static class Truck{
        int weight;
        int time;
        Truck(int weight){
            this.weight = weight;
            this.time = 0;
        }
    }

    public static int solution(int bridge_length, int weight, int[] truck_weights) {
        int answer = 1;
        int current = 0;
        int move;
        Vector<Truck> onBridge = new Vector<>();
        for (int i=0; i<truck_weights.length; i++) {
            if (onBridge.isEmpty() || current + truck_weights[i] <= weight){
                onBridge.add(new Truck(truck_weights[i]));
                current += truck_weights[i];
                move = 1;
            }
            else {
                i--;
                move = bridge_length - onBridge.get(0).time;
            }
            for (int j = 0; j < onBridge.size() ; j++) {
                onBridge.get(j).time+=move;
                if (onBridge.get(j).time == bridge_length){
                    current -= onBridge.get(j).weight;
                    onBridge.remove(j);
                    j--;
                }
            }
            answer+=move;
        }
        return answer+(bridge_length - onBridge.get(onBridge.size()-1).time);
    }
}

세 코드 효율성 비교

사실 두 코드의 풀이 방법은 똑같다.
다만 queue 자료 구조를 사용했느냐, vector 자료 구조를 사용했느냐의 차이다.

자료 구조의 차이에서 오는 특정 index의 데이터에 접근할 수 있느냐, 맨 처음에 들어온 데이터가 아닌 가장 마지막에 들어온 데이터에 바로 접근할 수 있느냐에 따라서 약간의 구현이 달라질 뿐이다.

queue를 이용하는 분류의 문제이지만, 먼저 들어온 데이터가 먼저 나온다는 FIFO의 원리만을 따와서 트럭에 적용시키되, 필요한 부분에 있어서는 특정 index의 데이터에 바로 접근할 수 있도록 하면 된다 !

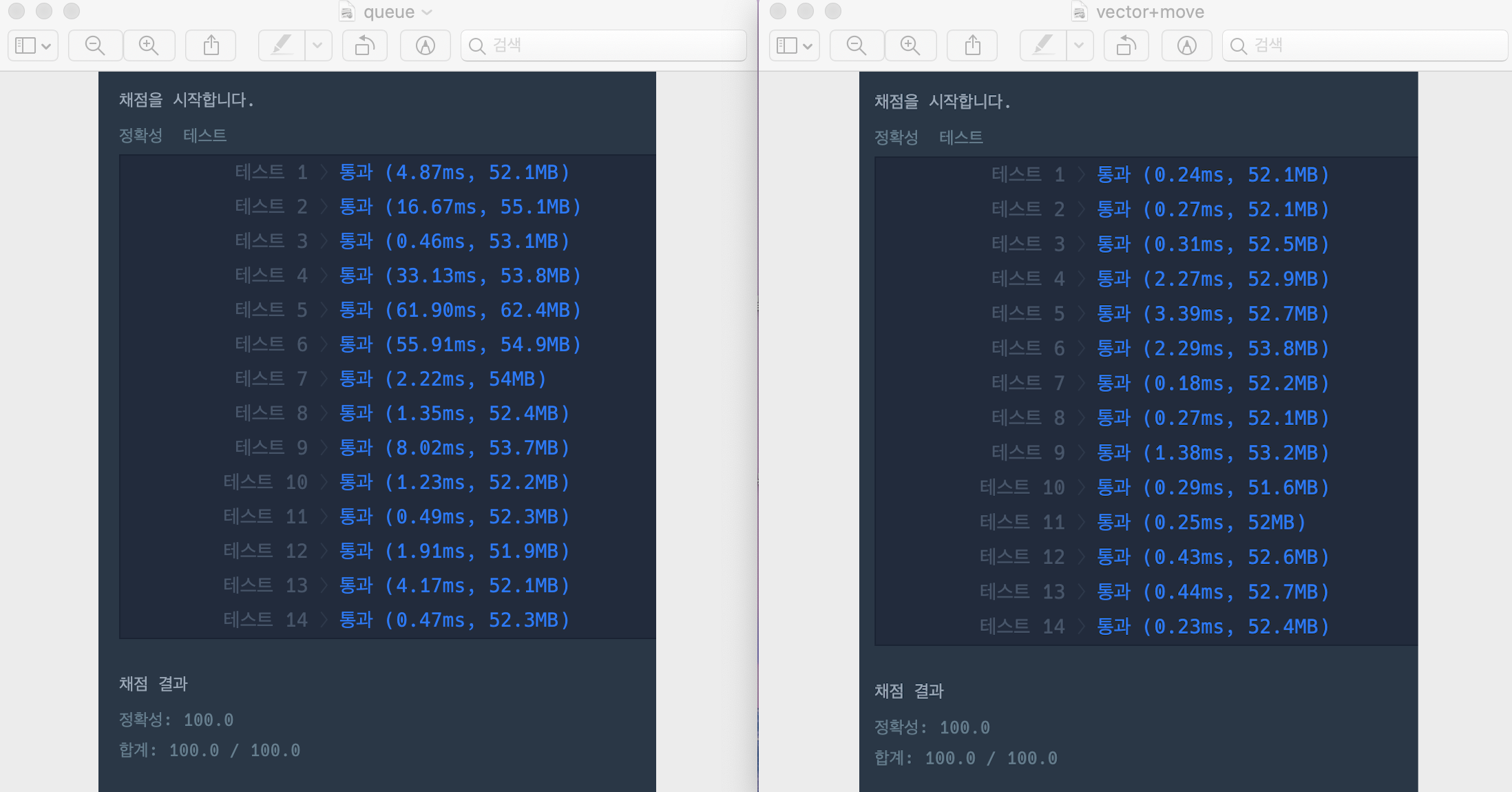
코드에서 보면, 마지막에 들어온 트럭의 남은 시간을 마지막에 더해줘야 하는데, 이 부분에서 시간의 차이가 발생하는 것 같다. 그 결과로 아래처럼 vector를 사용했을 때 시간이 미세하게 더 빠른 것을 확인할 수 있다.

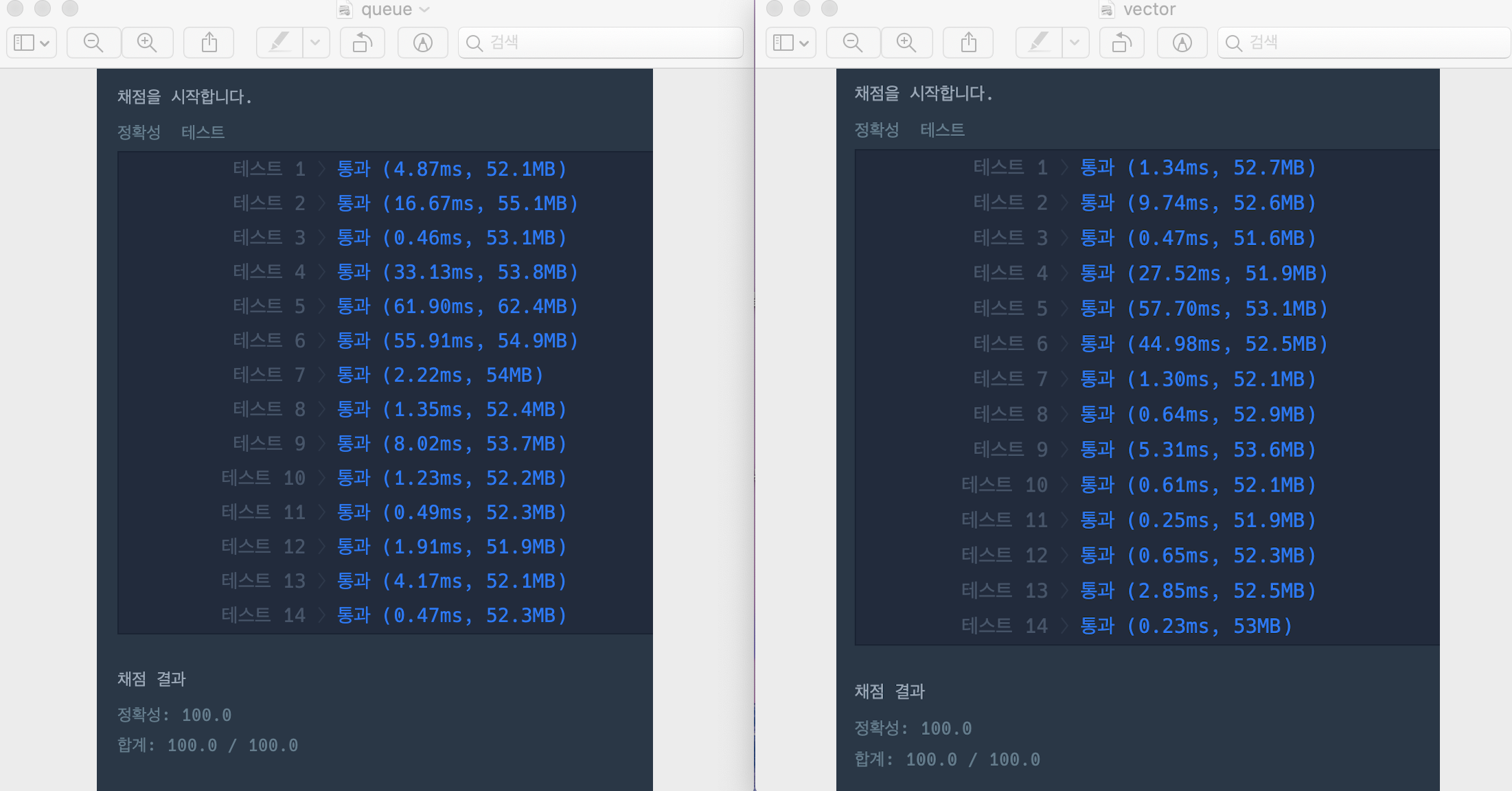
( 사실 큰 차이는 없지만, Queue 분류의 문제이거나 분류가 아니더라도 Queue의 FIFO를 사용하는 문제라고 해서 꼭 Queue 자료구조를 사용하려했던 나에게 그럴 필요 없다는 생각을 심어주는 의미로 작성해본다 🙂 )

+ ) 블로그 작성하면서 반영한 이동 거리 변수를 따로 둔 새로운 버전의 코드를 기존의 vector를 이용한 코드와 비교한 결과는 아래와 같다 ! 이건 눈에 띄게 시간이 줄어들었다 ( 당연하지 ㅋㅋ ! )

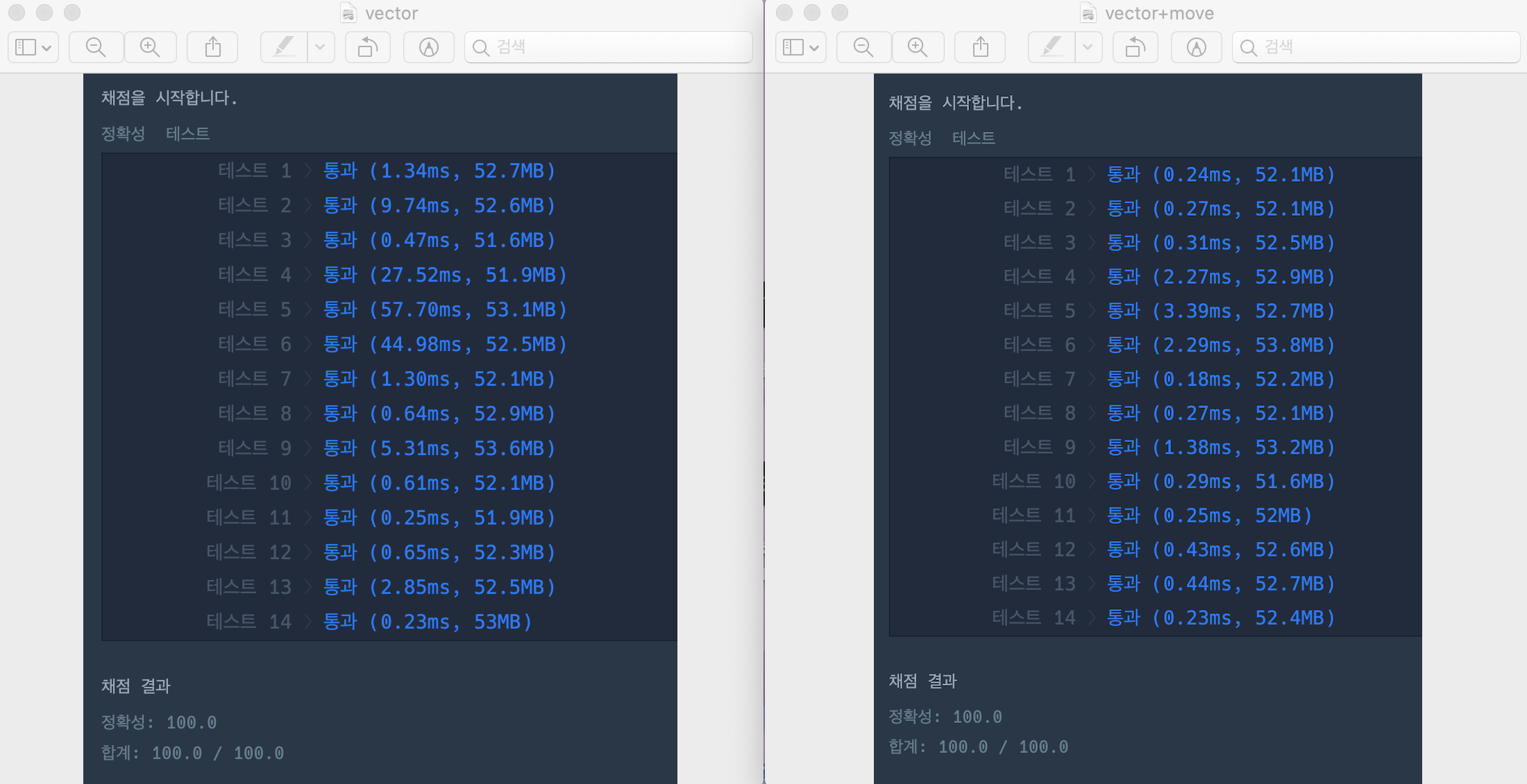
그럼 이만 !