오늘 푼 문제는 프로그래머스 고득점 kit DP 분류의 Level4 문제이다. ( 문제 링크 )
이로써 DP 분류도 뽀개기 완료 ✅ 이제 고득점 kit는 딱 두 문제 남았다 !
Level4 문제라서 풀 수 있을까 조금 걱정을 하고 시작했다. 1시간 안에 풀어보자고 마음 먹었고, 20분쯤 걸려서 풀이 방법이 떠올랐고 어떻게 코드로 옮길지도 생각했다. 실제로 한 시간 안에 문제를 제출했으나 문제점이 하나 있었고, 문제가 뭔지 바로 파악할 수 있었기에 금방 해결할 수 있었다. 자세한 건 아래에서 설명한다.
문제 설명
도둑이 어느 마을을 털 계획을 하고 있습니다. 이 마을의 모든 집들은 아래 그림과 같이 동그랗게 배치되어 있습니다. ( 글로도 이해할 수 있으므로 포스팅에 그림을 따로 첨부하지는 않습니다. 위에 링크해둔 문제 원문으로 가면 확인하실 수 있습니다. )
각 집들은 서로 인접한 집들과 방범장치가 연결되어 있기 때문에 인접한 두 집을 털면 경보가 울립니다.
각 집에 있는 돈이 담긴 배열 money가 주어질 때, 도둑이 훔칠 수 있는 돈의 최댓값을 return 하도록 solution 함수를 작성하세요.
제한사항
- 이 마을에 있는 집은 3개 이상 1,000,000개 이하입니다.
- money 배열의 각 원소는 0 이상 1,000 이하인 정수입니다.
입출력 예
| money | return |
|---|---|
| [1, 2, 3, 1] | 4 |
풀이 방법
각 집을 순차적으로 탐색하며 해당 집을 도둑질 할 것인지 말 것인지를 판단해야 한다. 그러므로 아래의 그림과 같이 해당 집을 도둑질 한 경우의 최대 금액과 도둑질 하지 않은 경우의 최대 금액을 구해나가며 최종적으로 가장 크게 훔칠 수 있는 금액을 구할 수 있다. ( 그림의 테스트 케이스는 연달아 훔치지 않는 것이 더 나은 경우를 고려할 수 있는지 판단하기 위해서 [4,1,1,5]와 같은 구간이 있게끔 예시를 정하였다 )
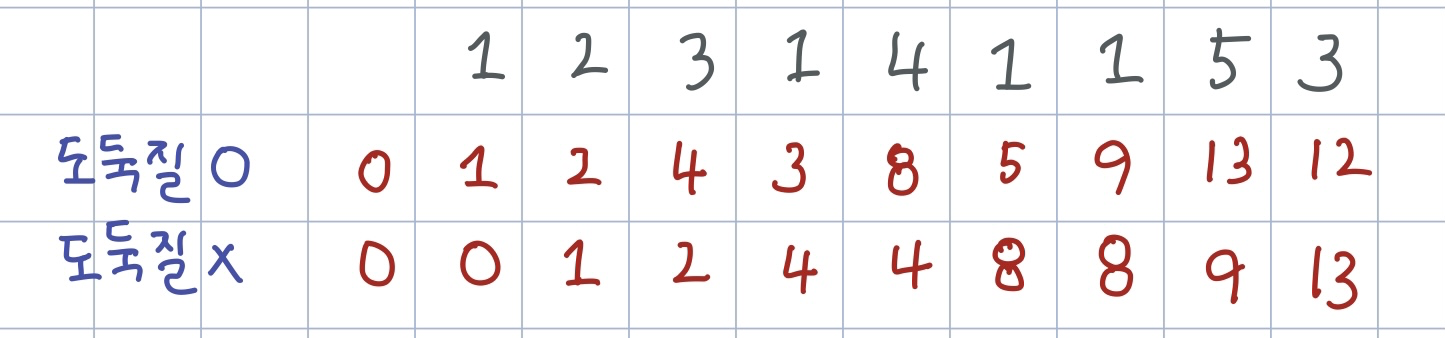
이 때, 각 금액은 이전까지 집을 거친 결과 값을 이용하며, 구하는 방법은 아래와 같다.
도둑질 한 경우의 최대 금액 = 이전 집을 도둑질 하지 않은 경우의 최대 금액 + 현재 집의 금액
> 이번 집을 도둑질 하기 위해서는 직전 집을 도둑질하지 않아야 하기 때문에 ! 도둑질 하지 않은 경우의 최대 금액 = 이전 집을 도둑질 유무와 무관한 최대 금액
( 즉, 이전 집을 도둑질 한 최대 금액과 도둑질 하지 않은 최대 금액 중에서 더 큰 값 )
> 이번 집을 훔치지 않을 때 가장 큰 값이어야 하기 때문에 ! 연달아 여러 집을 훔치지 않을수도 있음 !위의 방법에서 놓친 부분이 하나 있었다. 바로 문제의 조건은 원형이기 때문데 처음 집을 고른 경우는 마지막 집을 고를 수 없다는 것이다. DP를 이용하여 문제를 해결하였기 때문에 직전의 값만을 이용하여 현재 값을 구하였고, 이는 마지막집의 최대 값들을 설정할 떄 처음을 선택했는지 아닌지 판단할 수 없다는 것이다.
이 부분을 보완하기 위해서 기존에 도둑질O, 도둑질X 경우에 대해서만 값을 저장하던 것을 처음 집을 도둑질 한 경우와 아닌 경우로 나누어 총 4개의 값을 저장하며 문제를 풀었다. 이 경우에도 처음 원소에 대해서 두 경우의 고정값을 정해두는 것 외에는 위에 설명한 방법과 동일하다.
단, 마지막에 최종 결과 값을 반환할 때, 첫 집을 도둑질 한 경우는 마지막 집은 도둑질 할 수 없으므로 마지막 집을 도둑질 하지 않은 경우가 최대 값이지만, 첫 집을 도둑질 하지 않은 경우는 마지막 집을 도둑질 할 수도 하지 않을 수도 있으므로 이 세 값 중에서 가장 큰 값을 반환해야 하는 것이다.
코드
class Solution {
public int solution(int[] money) {
int[][] dp = {{money[0], 0}, {0,0}};
int temp;
for(int i=1; i<money.length; i++){
for(int j=0; j<2; j++){
temp = dp[j][0];
dp[j][0] = dp[j][1] + money[i];
dp[j][1] = Math.max(temp, dp[j][1]);
}
}
return Math.max(dp[0][1], Math.max(dp[1][0], dp[0][1]));
}
}