저는 아래의 책을 통해 정리하였지만, 해당 책은 수식에 대한 설명 위주라서 서치해서 찾은 자료를 함께 정리하였습니다. 참고 바랍니다.🏃♀️

퍼셉트론(Perceptron)
퍼셉트론(Perceptron) 은 학습이 가능한 초창기 신경망 모델이다. 이후 노드, 가중치, 층과 같은 새로운 개념이 도입되었다. 주어진 데이터를 선형 분리할 수 있다면 미분을 활용한 알고리즘은 100% 정확률로 수렴할 수 있다는 것이 증명되었다.
딥러닝을 포함하여 현대 신경망은 퍼셉트론을 병렬 구조와 순차 구조로 결합한 형태이다. 즉, 퍼셉트론은 현대 신경망의 중요한 구성 요소이므로 구조와 동작, 학습 알고리즘, 특성을 제대로 이해할 필요가 있다.
1. 구조
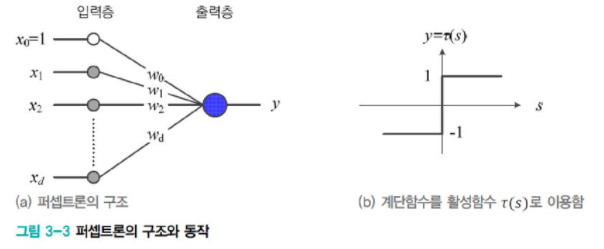
퍼셉트론의 구조는 그림 3-3(a)을 참고하면 된다. 입력층과 출력층이라 불리는 2개의 층이 있고, 입력층은 아무 연산을 하지 않아 층의 개수를 세지 않는다. 따라서 퍼셉트론은 1개의 층이 있다고 말할 수 있다.
층을 구성하는 노드는 원으로 표시하며, 입력층에 있는 입력 노드 하나는 특징 벡터의 특징 하나를 의미한다.
따라서 특징 벡터를 x = (x_1,x_2, ..., x_d)T로 표기한다면 입력층은 d개의 노드를 가진다. 맨 위에 x_0으로 표기된 bias라 부르는 여분의 노드가 있어서 d+1개의 입력 노드가 있다.
출력층은 y라 표기된 하나의 노드를 가진다. 입력 노드는 모두 출력 노드와 에지로 연결되어 있는데, 에지는 w_i로 표기된 가중치(weight)를 가진다. 따라서 d+1개의 가중치가 있다.
2. 동작
퍼셉트론의 동작은 단순하다. 입력층에 특징 벡터 x = (x_1,x_2, ..., x_d)T가 들어 오면, 서로 연결된 특징값과 가중치를 곱한 결과를 모두 더한다. 이렇게 얻은 값 s(그림3-3(b))를 활성화 함수(activation function)에 입력으로 넣고 계산한다.
activation function의 출력이 퍼셉트론의 최종 출력이 되는데, 1 또는 -1이 된다.
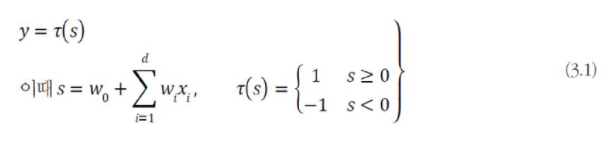
해당하는 특징값과 가중치를 곱한 결과를 모두 더하여 s를 구하고, activation function r을 적용하여 최종 출력 y는 +1 또는 -1이 된다.
예제 3-1
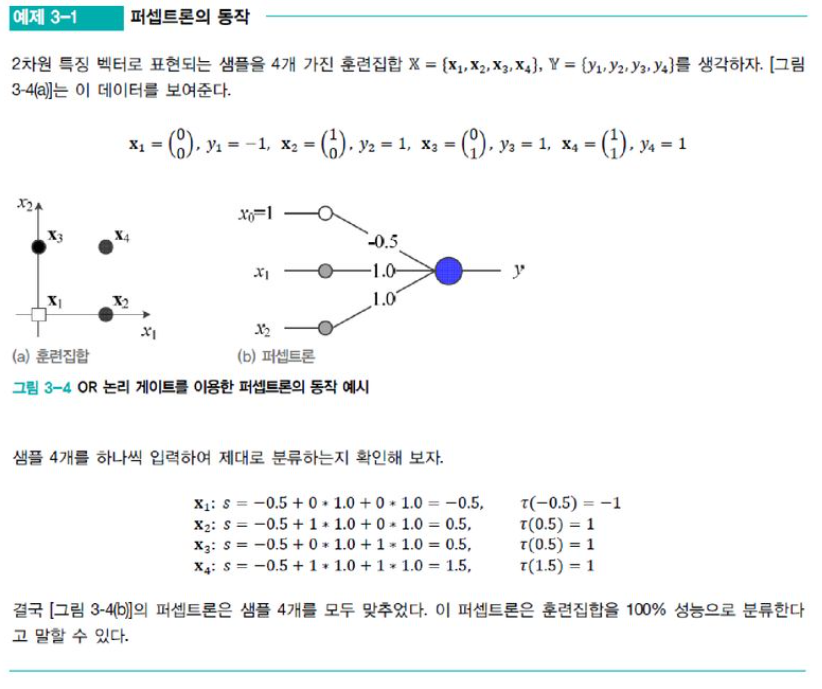
[예제 3-1]에서 x를 100% 정확하게 분류하는 퍼셉트론은 무수히 많다. 예를 들어, x_2노드에 연결된 가중치를 0.9로 바꾸어도 성능은 같다. 이러한 성질은 일반적으로 성립한다.
즉, 어떤 훈련 집합을 같은 성능으로 분류하는 퍼셉트론은 무수히 많다는 것이다.
행렬 표기

행렬곱 wTx는 벡터의 내적 w*x로 표기해도 된다.
식 3.2에서는 bias를 별도로 취급하였는데, bias 노드의 값 1을 벡터에 추가하여 feature vector(특징 벡터)를 d+1 차원으로 확장하면, 식 3.3처럼 더 간결하게 표현할 수 있다.
식 3.3을 이용해서 퍼셉트론의 동작을 y = r(wTx)로 표현할 수 있고, 행렬을 이용한 간결한 표현법은 이후에도 계속 나온다.
분류기로 해석
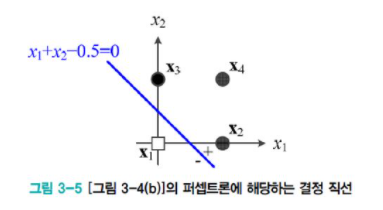
[그림3-5]는 퍼셉트론의 동작을 기하학적으로 설명한 그림이다. 이 퍼셉트론은 2차원 특징 공간을 파란색 직선을 따라 +, - 영역으로 나누었다.
- 영역은 +1로, - 영역은 -1로 분류하는 이진 분류기이다.
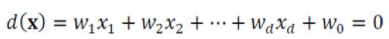
해당 식은 직선의 방정식이며, 퍼셉트론의 가중치가 직선을 정하게 된다. w1, w2, ..., wd는 직선의 방향을, w0는 절편을 결정한다.
이처럼 특징 공간을 2개의 영역으로 나눔으로써 패턴의 부류를 결정하는 경계를 decision boundary라고 한다. 퍼셉트론은 선형 방정식으로 사용하므로, 2차원에서는 결정 경계가 직선이 되는데 이 직선을 decision line이라고 한다.
[그림3-4(b)]나 [그림3-5]는 표현 방법만 다를 뿐, 모두 퍼셉트론이 선형 분류기(linear classifier)라는 사실을 나타낸다.
3. 학습
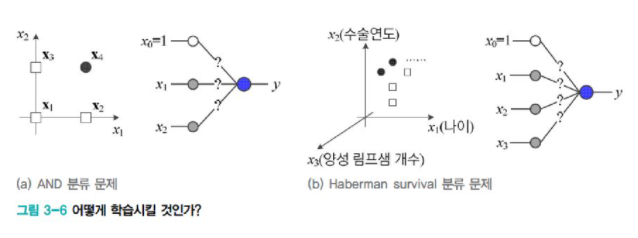
위는 2차원 공간에 4개의 샘플이 있는 train set이었지만, 현실은 d차원의 공간에 수백~수만 개의 샘플이 존재한다. 여기서 매개변숫값을 어떻게 찾아낼 것인가?
목적함수 설계
퍼셉트론의 매개변수를 w = (w0, w1, w2, ..., wd)T라 표기하면, 매개변수 집합은 θ = {w}이다.
목적함수를 J(θ) 또는 J(w)로 쓸 수 있다.
목적함수는 다음 조건을 만족해야 한다.
목적함수 조건
- J(w) ≥ 0
- w가 최적이면, 즉 모든 샘플을 맞히면 J(w)=0이다.
- 틀리는 샘플이 많은 w일수록 J(w)는 큰값을 가진다.
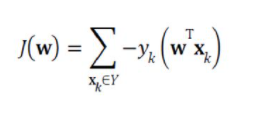
J(w) 식은 위와 같이 나타낸다. Y는 w가 틀리는 샘플의 집합이다. 이 식을 편미분하면 아래와 같이 나타난다.

가중치 갱신 규칙인 θ = θ - pg를 적용하고, 그레디언트 g를 계산하기 위해 J(w)를 편미분하면 식 3.8을 얻는다. x_ki는 x_k의 i번째 요소이다.
즉, x_k = (x_k0, x_k1, ..., x_kd)T이다.
식 3.8을 가중치 갱신 규칙(θ = θ - pg)에 대입하면 식 3.9가 나온다. 목적함수가 커지는 방향이므로 -를 붙여 계산하고 p는 학습률이다.
행렬 표기

행렬 표기 방식은 위의 이미지를 참고!
