Graph 강의 정리
강의 자료 출처: CS224W Lecture 3
정리는 위 출처의 자료를 바탕으로 모든 페이지를 옮겨 정리한 것입니다. 그래프를 처음 공부해서 잘못 이해한 내용이 있을 수 있습니다. 오류를 댓글로 알려주시면 수정하겠습니다. 감사합니다.
Index
- Node Embeddings
- Encoder and Decoder
- Random Walk Approchaes for Node Embeddings
- Embedding Entire Graphs
1. Node Embeddings
Recap: Traditional ML for Graphs
입력 그래프가 주어졌을 때, node, link와 graph-level features 추출하고 features에서 labels로 mapping하는 SVM, neural network 등의 모델을 학습합니다.
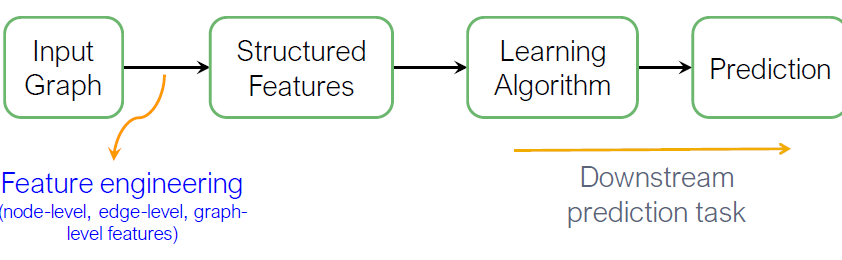
그래프 표현 학습은 매번 single time마다 feature engineering의 필요를 저하시킵니다. Representing Learning은 자동적으로 features를 학습합니다.
Graph Representing Learning
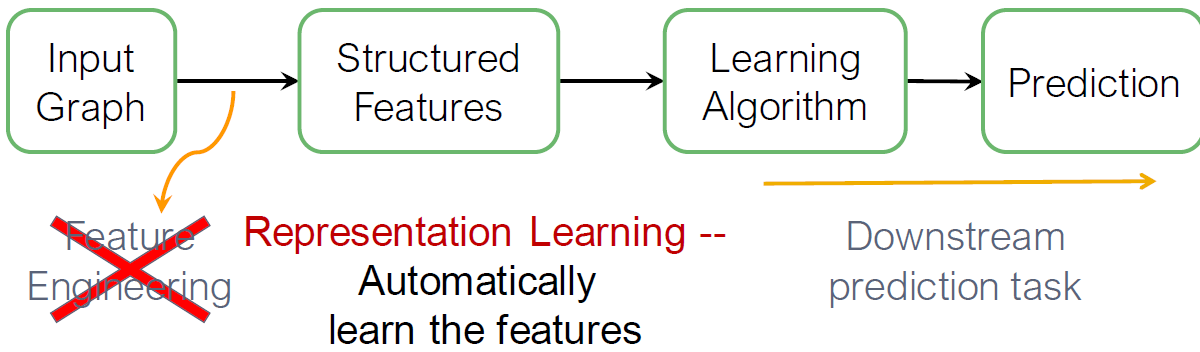
Goal: Efficient task-independent feature learning for machine learning with graphs
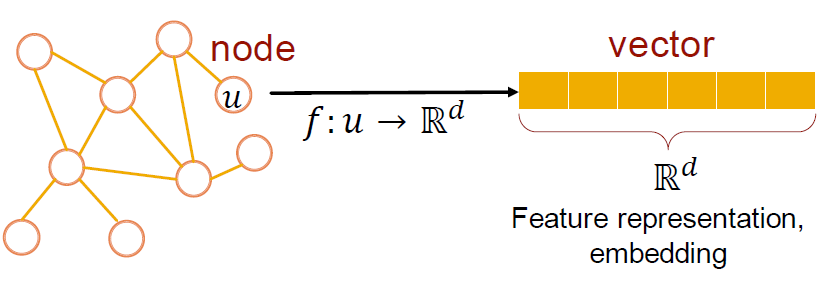
Why Embedding?
Task: Map needs into an embedding space
- 노드 사이의 임베딩 유사도는 네트워크의 유사도를 의미합니다.
- 예: 두 노드는 서로 가깝습니다 (edge로 연결되어 있음)
- 네트워크 정보를 Encode합니다.
- 잠재적으로 많은 downstream predictions에 사용됩니다.
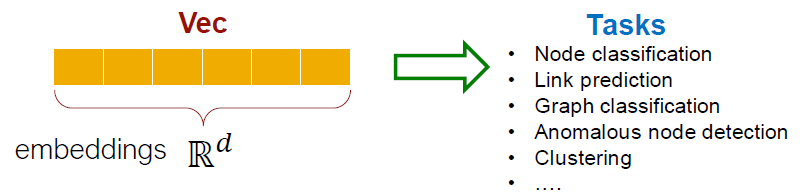
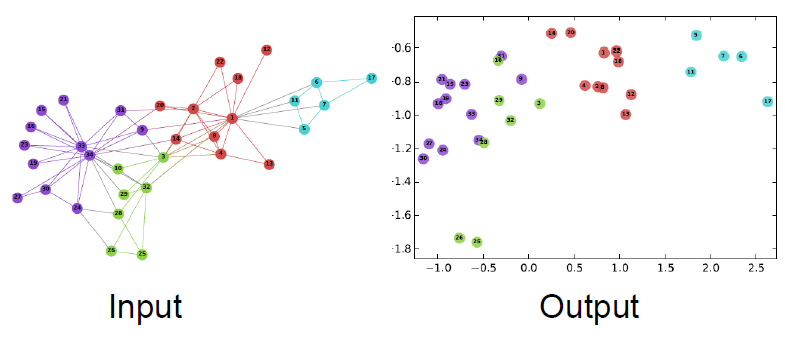
Example Node Embedding
노드의 2D 임베딩입니다.
2. Encoder and Decoder
Setup
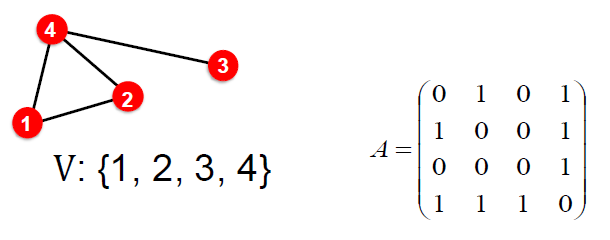
그래프 G가 있다고 가정합니다.
- V는 vertex set입니다.
- A는 binary라고 가정한 adjacency matrix(인접 행렬)입니다.
- 간단히하기 위해 node features와 추가 정보가 사용되지 않습니다.
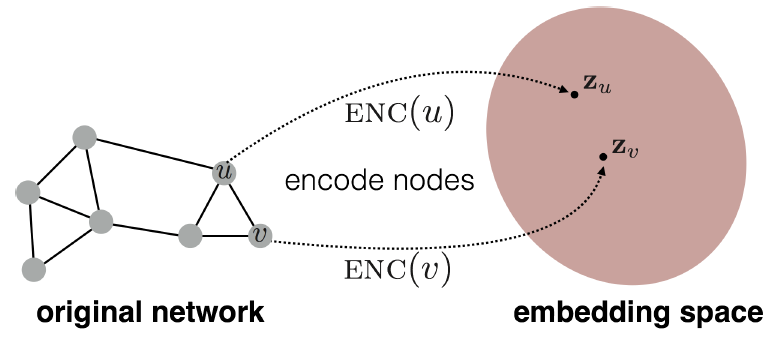
Embedding Nodes
- 목표는 위해 임베딩 공간에서의 유사성이 그래프의 유사성에 근접하도록 노드를 인코딩하는 것입니다.
수식으로 다시 표현하면
우
원래 네트워크의 유사성과 임베딩의 유사성을 비교하여 근접하도록 인코딩함을 의미합니다. 따라서 ENC(u)와 ENC(v)를 정의할 필요가 있습니다.
Learning Node Embeddings
- 인코더는 노드에서 임베딩으로 매핑합니다.
- 노드 유사성 함수를 정의합니다. (예를 들어, 원래 네트워크의 유사성을 측정합니다.)
- 디코더 DEC는 임베딩에서 유사성 점수로 매팽합니다. (DEC()
- 인코더의 매개변수를 최적화합니다.
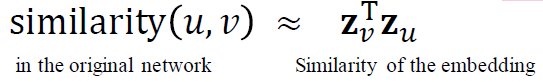
Two Key Components
- Encoder는 각 노드를 낮은 차원의 벡터로 매핑합니다.
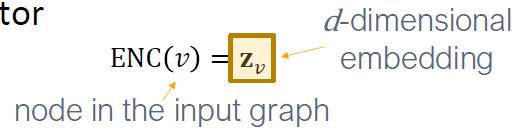
- 유사성 함수: 벡터 공간의 관계가 원래 네트워크의 관계에 매핑되는 방식을 지정합니다.
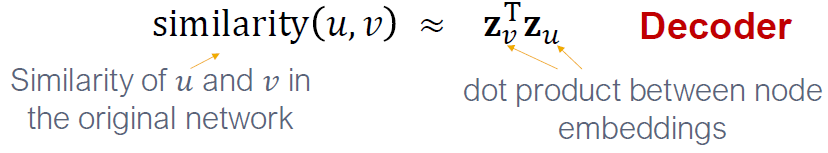
“Shallow” Encoding
가장 간단한 인코딩 접근은 Encoder를 embedding-lookup으로 보는 것입니다.
- 행렬, 각 칼럼은 우리가 학습하고 최적화 해야할 노드 임베딩입니다.
- indicator vector, 모든 zeroes는 노드 v를 나타내는 열 중 하나입니다.
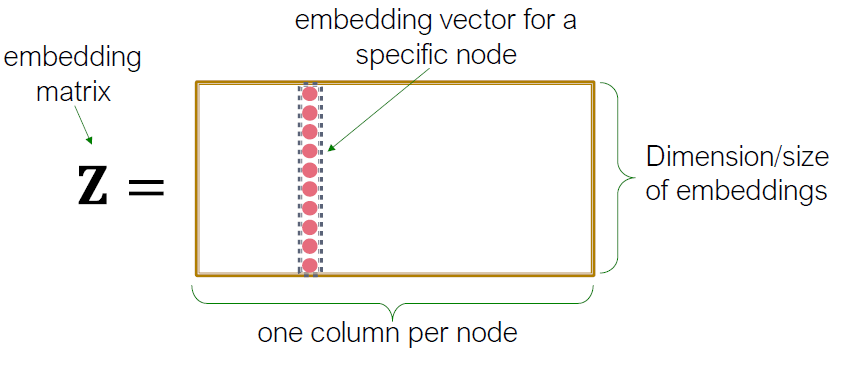
- 각 노드에는 고유한 임베딩 벡터가 할당됩니다 (즉, 각 노드의 임베딩을 직접 최적화합니다).
- 많은 방법들:
DeepWalk,node2vec
Framework Summary
Encoder와 Decoder의 Framework
- 얇은 인코딩: 임베딩 룩업
- 최적화하는 매개변수: 인 모든 노드에 대해 노드 임베딩 를 포함하는 Z
- Lecture 6에서 deep encoder(GNNs)를 다룹니다.
- Decoder: 노드 유사도 기반의 디코더
- Objective: 유사성을 가지는 노드 쌍 의 를 최대화하는 것
How to Define Node Similarity?
가장 중요한 것은 노드의 유사성을 어떻게 정의하는지입니다.
두 노드는 유사 임베딩을 갖고 있다면
- are linked?
- share neighbors?
- have similar “structural roles?”
를 고려할 수 있습니다.
우리는 random walks를 사용해서 노드 유사성 정의와 유사도 측정을 위해 임베딩을 최적화하는 방법을 학습합니다.
Note on Node Embeddigns
노드 임베딩을 학습하는 비지도/지도학습이 있습니다.
- 노드 라벨을 사용하지 않습니다
- 노드 특성을 사용하지 않습니다.
- 목표는 네트워크 구조의 일부 측면(DEC에 의해 캡처됨)이 보존되도록 노드의 좌표 집합(즉, 임베딩)을 직접 추정하는 것입니다.
- 이 임베딩들은 task idependent합니다.
- 특정 task를 위해 훈련되지 않지만 모든 작업에서 사용될 수 있습니다.
3. Random Walk Approchaes for Node Embeddings
Notation
- Vector : 노드 의 임베딩(찾으려고 목표를 하는 것)
- Probability : 기반의 모델 예측값, 노드 𝑢에서 시작하는 랜덤 워크에서 노드 𝑣를 방문할 (예측된) 확률입니다.
예측된 확률은 비선형 함수에서 생성됩니다.
- Softmax function: K의 실제값 벡터를 합이 1이 되는 K의 확률값으로 바꿉니다.
- Sigmoid function: S-shaped 함수는 범위 (0, 1)로 실제 값들을 변화 시킵니다.
Random Walk
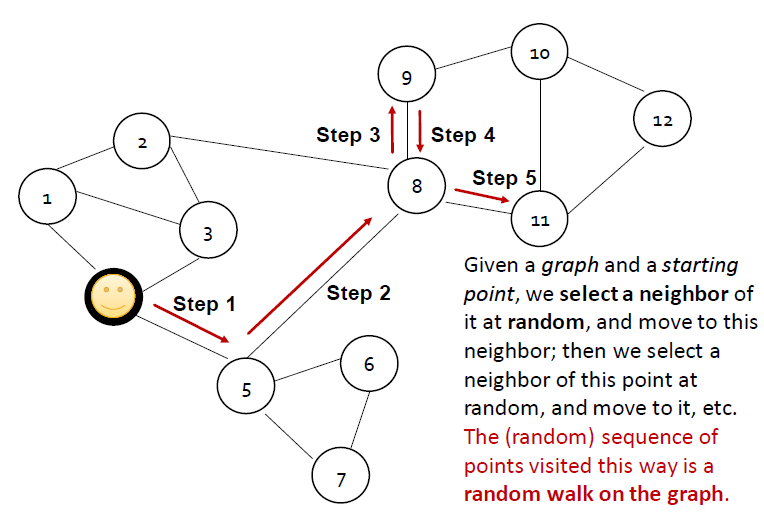
- 그래프가 주어졌을 때 point에서 시작합니다.
- 시작 포인트에서 랜덤하게 이웃을 고르고, 이웃으로 이동합니다.
- 그리고 그 점에서 랜덤하게 또 이웃을 선택하고 움직입니다.
- 이 길을 방문한 점들의 (랜덤) 시퀀스는 그래프의 random walk입니다.
probability
(그래프 위에서 와 가 무작위로 걸을 때 발생할 확률)
Random-Walk Embeddings
- 전력 R을 사용하는 랜덤 워크로 노드 u에서 시작해 노드 v를 방문할 확률을 측정합니다.
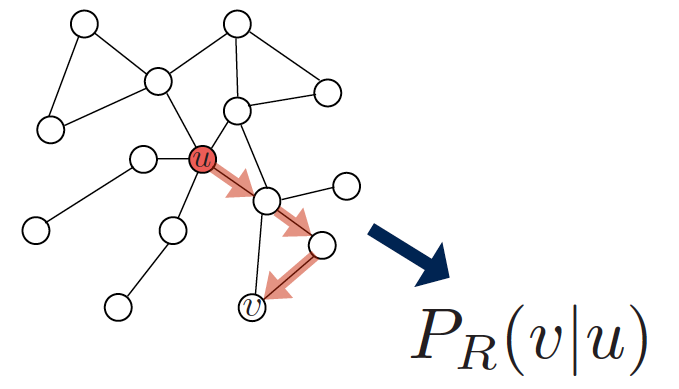
- 랜덤 워크 전략을 인코딩하는 임베딩을 최적화합니다.
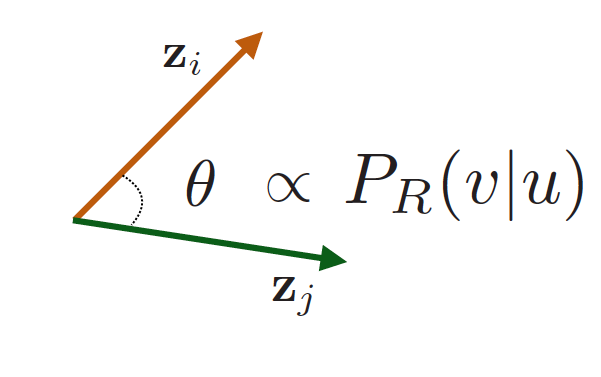
임베딩 공간의 유사성()은 랜덤 워크의 유사성으로 인코딩합니다.
Why Random Walks?
-
Expressivity(표현성): local 및 상위 이웃 정보를 모두 통합하는 노드 유사성의 유연한 확률적 정의
아이디어: 노드 에서 시작하는 랜덤 워크가 높은 확률로 를 방문하면 와 가 유사합니다. (high-order multi-hop information)
-
Efficiency(효율성): 훈련할 때 모든 노드 쌍을 고려할 필요가 없습니다. 랜덤 워크에서 함께 발생하는 쌍만 고려하면 됩니다.
Unsupervised Feature Learning
- Intuition: 유사성을 유지하는 d차원 공간에서 노드의 임베딩을 찾습니다.
- Idea: 네트워크에서 근처 노드는 서로 가깝다는 것처럼 노드 임베딩을 학습합니다.
- 노드 가 주어졌을 때, 근처 노드를 어떻게 정의하나요?
- 는 랜덤 워크 전략 에 의해 얻은 의 이웃입니다.
Feature Learning as Optimization
Given , 목표는 매핑을 학습하는 것입니다.
Log-likelihood objective:
- 는 전략 에 의한 노드 의 이웃입니다.
Given node , 이웃 랜덤 워크에서 노드의 예측의 feature representations을 학습하기를 원합니다.
Random Walk Optimization
- 랜덤 워크 전략 을 사용하여 그래프의 각 노드 에서 시작하여 짧은 고정 길이 랜덤 워크를 실행합니다.
- 각 노드 collect 에 대해 부터 시작하여 랜덤 워크에서 방문한 노드의 다중 집합
- 다음에 따라 임베딩 최적화: 주어진 노드 , 이웃 예측
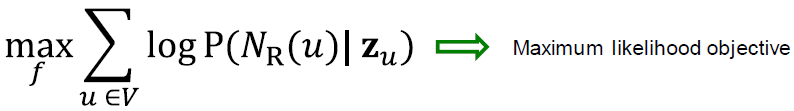
- 는 랜덤 워크에 의해 여러 번 방문하는 노드 때문에 반복되는 요소를 갖습니다.
동등하게,
- Intuition: 동시에 발생하는 랜덤 워크의 likelihood를 최대화하기 위한 임베딩 를 최적화합니다.
- 소프트맥스를 사용해서 를 매개변수화합니다.
- 왜 소프트맥스입니까? 노드 가 모든 노드 에서 노드 와 가장 유사하기를 원합니다.
- Intuition:
위의 식들을 모두 한 꺼번에 적으면 아래의 꼴이 됩니다.
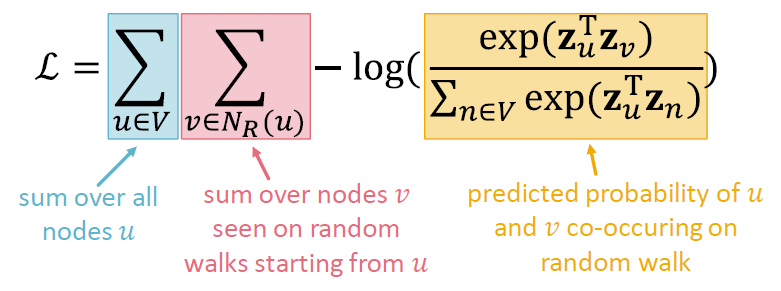
랜덤 워크 임베딩의 최적화는 을 최소화하는 임베딩 를 찾는 것과 같습니다.
그러나 이 작업은 너무 비용이 큽니다. 식에 벡터를 곱한 제곱 값의 지수함수를 두 번 더한다는 것이 연산 자체에 무리가 갑니다.
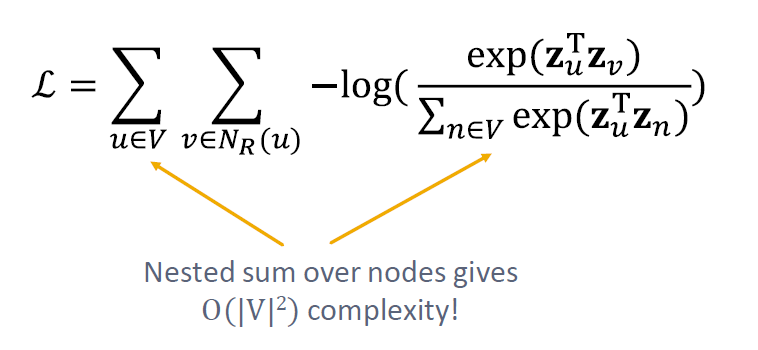
분모에 있는 해당 식이 계산 비용에 부담을 주는 범인입니다. 이것을 어떻게 근사 시킬 수 있을까요?
Negative Sampling
해결 방법은 Negative sampling입니다.

모든 노드의 정규화를 대신해서, k 무작위를 negative samples 에 대해 정규화합니다. Negative sampling은 likelihood의 빠른 계산을 따릅니다.
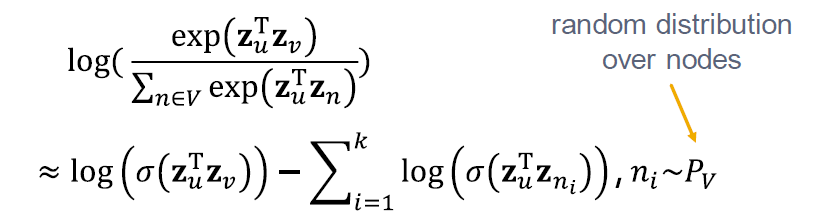
노드에 걸친 랜덤 분포를 따릅니다.
- 각 확률이 있는 샘플 k negative 노드들은 각 degree에 비례합니다.
negative sample 수에 대해 k는 두 가지 고려 사항이 있습니다.
- k가 높을수록 더 robust한 측정을 제공합니다.
- k가 높으면 negative events에서 높은 bias와 대응됩니다.
negative sample은 임의의 노드이거나 보행 중이 아닌 노드일 수 있습니까? 사람들은 종종 모든 노드를 사용합니다(효율성을 위해). 그러나 가장 "정확한" 방법은 보행 중이 아닌 노드를 사용하는 것입니다.
Stochastic Gradient Descent
objective function을 얻은 후에 그것을 어떻게 최적화 시킵니까?
Gradient Descent는 을 최소화하는 간단한 방법입니다.
- 모든 노드 에 대해 임의의 값 를 초기화합니다.
- 수렴될 때까지 반복합니다.
- 모든 에 대해 미분값 를 계산합니다.
- 모든 에 대해 미분의 반대 방향으로 step을 만듭니다.
- : learning rate
Random Walks: Summary
- 짧은 고정된 길이의 랜덤 워크는 그래프에서 각 노드로부터 시작합니다.
- 각 노드 는 를 수집하기 위해, 에서 시작해 랜덤워크에서 방문한 노드의 다중 집합입니다.
- SGD를 사용한 임베딩을 최적화합니다.
negative sampling을 사용하여 효율적으로 근사가 가능해집니다!
How should we randomly walk?
지금까지 랜덤 워크 전략 R에서 임베딩을 최적화하는 방법을 설명했습니다. 이러한 랜덤 워크를 실행하기 위해 어떤 전략을 사용해야 합니까?
가장 간단한 아이디어는 각 노드에서 시작하여 고정된 길이의 편향되지 않은 랜덤 워크를 실행하는 것입니다.
문제는 그러한 유사성의 개념이 너무 제한적이라는 것입니다. 이것을 어떻게 일반화할 수 있습니까?
Overview of node2vec
Goal:
목표는 feature space에서 가까운 유사한 네트워크 이웃이 있는 노드를 포함하는 것입니다. 이 목표를 downstream prediction task와 독립적인 maximum likelihood optimization(최대 우도 최적화) 문제로 구성합니다.
Key observation:
노드 의 네트워크 이웃 에 대한 유연한 개념은 풍부한 노드 임베딩으로 이어집니다. 노드 의 네트워크 이웃 을 생성하기 위해 편향된 2차 랜덤 워크 𝑅를 개발합니다.
node2vec: Biased Walks
아이디어는 네트워크에서 local 과 global 관점의 유연하고 편향된 랜덤 워크를 사용하는 것입니다.
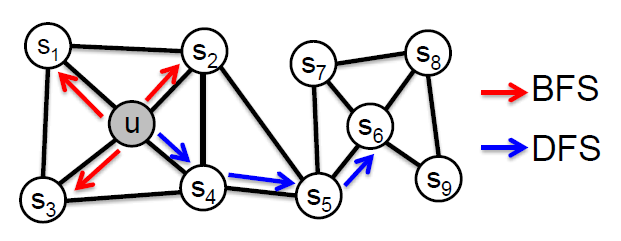
)
노드 가 주어졌을 때, 이웃 를 정의하는 두 가지 고전 적인 방법이 BFS, DFS입니다.
길이 3의 Walk를 살펴보면
, Local microscopic view
, Global macroscopic view
BFS vs. DFS
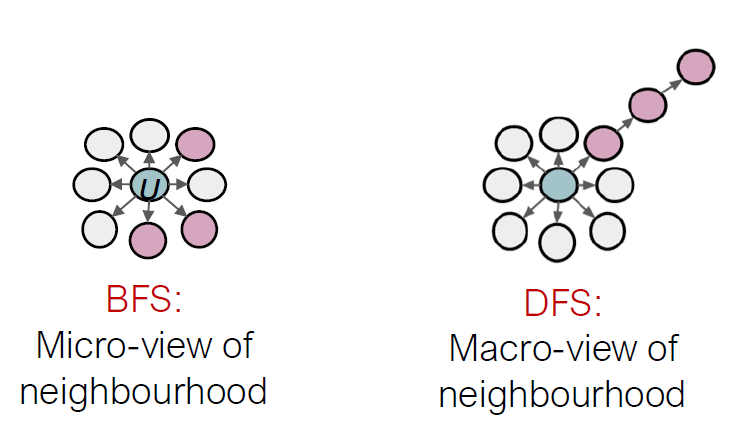
Interpolationg BFS and DFS
주어진 노드 가 이웃 을 생성하는 편향된 고정 길이 랜덤 워크
- 두 매개변수:
- Return parameter p: 이전 노드로 돌아가기
- In-out parameter q: 바깥쪽으로 이동(DFS) vs. 안쪽으로 이동(BFS), 직관적으로 는 BFS 대 DFS의 "비율(ratio)"입니다.
Biased Random Walks
편향된 2차 랜덤 워크는 네트워크의 이웃을 탐색합니다. edge 를 건너고 현재 에 있습니다. 의 이웃은 다음과 같을 수 있습니다.
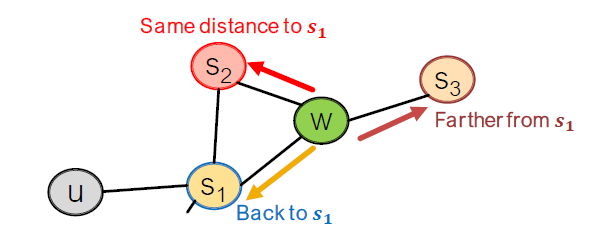
어디에서 왔는지 walk를 기억하는 것이 Idea입니다.
Walker는 edge 를 넘어가고, 에 있습니다. 다음은 어디입니까?
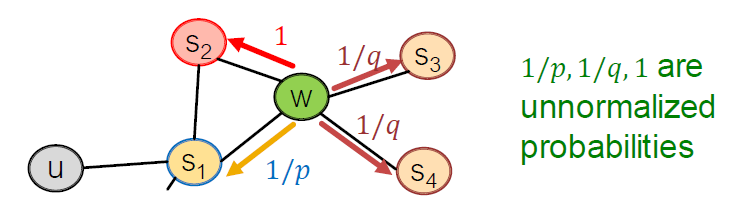
모델 전환 확률
- : 파라미터를 반환
- : “walk away” 파라미터
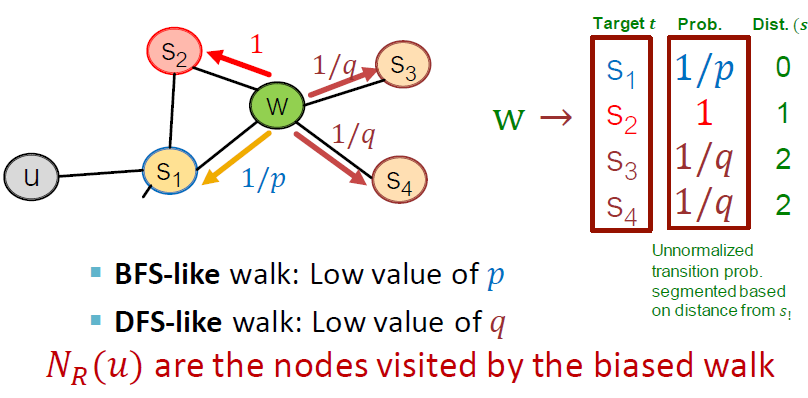
현재 지점 에서 목표가 되는 Target 와 확률, 거리를 계산합니다. 는 biased walk가 방문한 노드입니다.
node2vec algorithm
- random walk 확률을 계산합니다.
- 각 노드 에서 시작하는 랜덤 워크 길이 을 시뮬레이션합니다.
- SGD를 사용해서 node2vec의 objective를 최적화합니다.
선형 시간의 복잡도를 갖습니다. 모든 3가지 단계가 개별적으로 병렬화가 가능합니다.
Other Random Walk Ideas
- Different kinds of biased random walks:
- Based on node attributes ( Dong et al., 2017).
- Based on learned weights ( Abu El Haija et al., 2017).
- Alternative optimization schemes:
- Directly optimize based on 1 hop and 2 hop random walk probabilities (as in LINE from Tang et al. 2015).
- Network preprocessing techniques:
- Run random walks on modified versions of the original network (e.g., Ribeiro et al. 2017’s struct2vec , Chen et al. 2016’s HARP).
Summary so far
핵심 아이디어:
임베딩 공간에서의 거리 때문에 임베딩된 노드는 원래 네트워크의 노드 유사성을 반영하도록 합니다.
노드 유사성의 다른 정의:
- Naive: 두 노드가 연결되어 있다면 유사합니다
- Neighborhood overlap (Lecture 2)
- Random walk 접근 방법 (Today!)
그래서 어떤 방법을 사용하란 것입니까?
모든 경우에서 사용하는 하나의 방법은 없습니다. 예를 들어 node2vec는 노드 분류에서 더 잘 수행되는 반면 대체 방법은 링크 예측에서 더 잘 수행됩니다.
랜덤 워크 접근법은 일반적으로 더 효율적입니다.
따라서 일반적으로 애플리케이션과 일치하는 노드 유사성의 정의를 선택해야 합니다.
4. Embedding Entire Graphs
Embedding Entire Graphs
- Goal: 하위 그래프 또는 전체 그래프 를 포함하고 싶습니다. 그래프 임베딩:
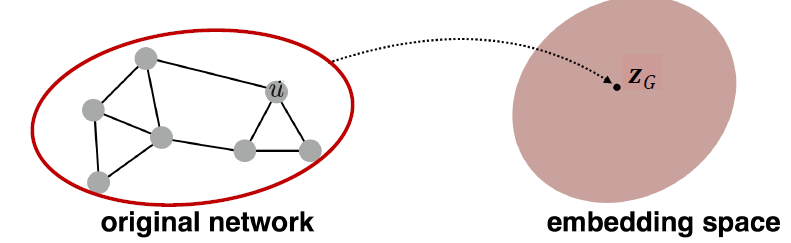
- Tasks:
- Classifying toxic vs. non toxic molecules
- Identifying anomalous graphs
Approach 1
- (서브)그래프 𝐺에서 표준 그래프 임베딩 기술 실행
- 그런 다음 (하위) 그래프 𝐺에서 노드 임베딩을 합산(또는 평균)합니다.
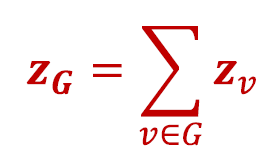
Approach 2
- (서브)그래프를 나타내는 "가상" 도입 및 표준 그래프 임베딩 기술 실행
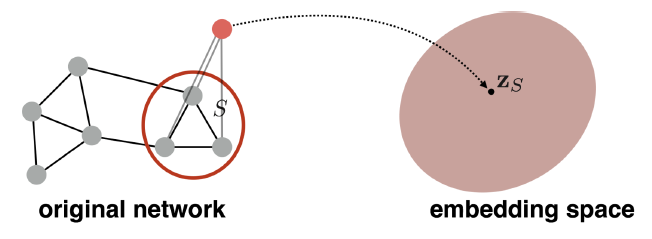
Approach 3: Anonymous Walks Embedding
- anonymous walks의 상태는 랜덤 워크에서 노드를 처음 방문한 인덱스에 해당합니다.
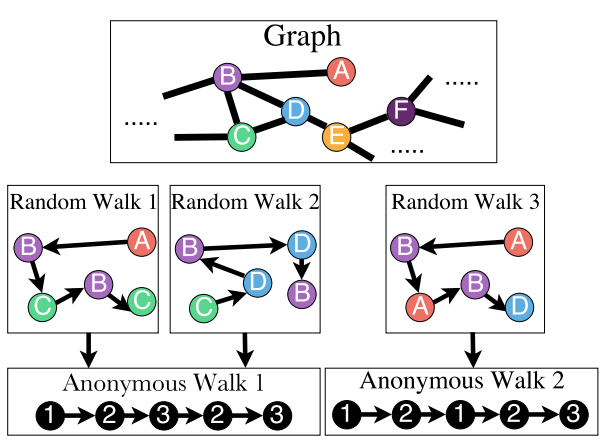
- 방문한 노드의 신원에 구애받지 않음(따라서 익명)
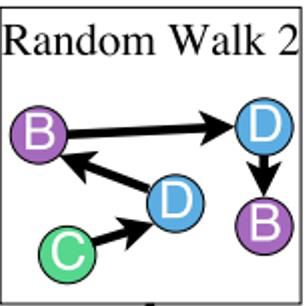
- 예: Random walk :
- Step 1 : node A → node 1
- Step 2 : node B → node 2 (different from node 1)
- Step 3 : node C → node 3 (different from node 1, 2)
- Step 4 : node B → node 2 (same as the node in step 2)
- Step 5 : node C → node 3 (same as the node in step 3)
- Note: Random walk 는 같은 anonymous walk를 제공합니다.
Number of Walks Grows
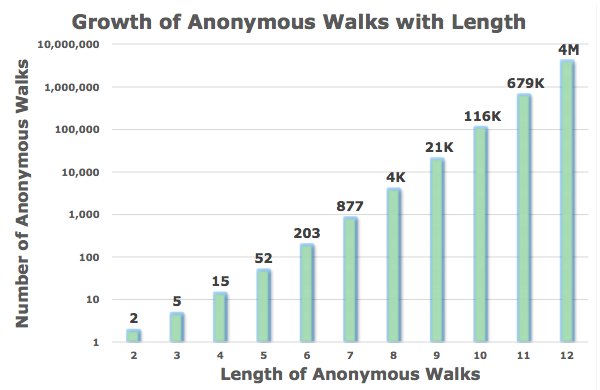
anonymous walks 수는 기하급수적으로 증가합니다.
5개의 anonymous walks, 길이 3의 walks 가 있습니다.
Simple Use of Anonymous Walks
- 단계를 거치는 anonymous walks 를 시뮬레이션하고 그 수를 기록합니다.
- 이 walks를 걸쳐서 확률 분포로 그래프를 표현합니다.
예를 들어,
- set
- 5-dim vector의 그래프를 표현할 수 있다면
- 길이 3의 5개의 anonymous walks 를 가집니다. : 111, 112, 121, 122, 123
- = 그래프 에서의 anonymous walks 의 확률을 의미합니다.
Sampling Anonymous Walks
anonymous walks의 Sampling은 m 랜덤 워크의 집합이 개별적으로 생성됩니다. 이 walks를 거친 확률 분포의 그래프를 표현합니다.
얼마나 많은 random walk m을 필요로 하나요?
분포에 미만 이상의 확률을 가진 오류가 있기를 원합니다.
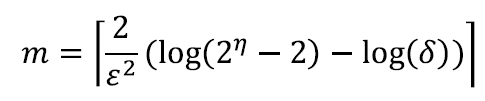
예를 들어:
𝜂=877명의 randolw walk 길이 𝑙=7이 있습니다. 𝜀=0.1 및 𝛿=0.01로 설정하면 𝑚=122,500 랜덤 워크를 생성해야 합니다.
New idea: Learn Walk Embedding
각 걷기가 발생하는 시간의 일부로 단순히 나타내는 대신 anonymous walk 의 𝒘 임베딩을 학습합니다.
모든 anonymous walk 와 함께 그래프 임베딩 를 학습합니다.
, 여기서 는 anonymous walk의 샘플링 된 수입니다.
How to embed walk?
아이디어는 Embed walks가 다음 walk가 예측할 수 있다는 것입니다.
Learn Walk Embeddings
- Output: A vector for input graph 𝑮
- The embedding of entire graph to be learned
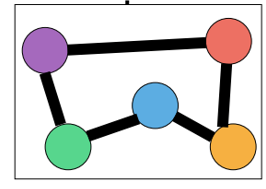
- Starting from node 1 : Sample anonymous random walks, e.g.
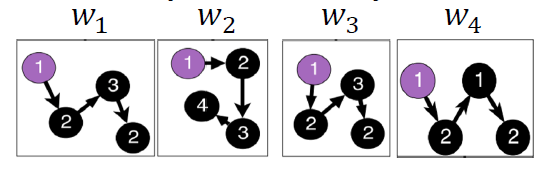
𝚫 size window에서 공동 발생하는 walk를 예측하는 방법을 배웁니다. (예: Δ=2이고, 가 주어졌을 때 을 예측합니다.)
Objective:
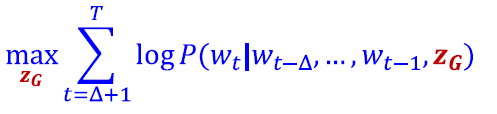
T는 walks의 총 수입니다.
- 각각의 길이 을 가진 에서 𝑻 다른 랜덤 워크를 실행합니다.
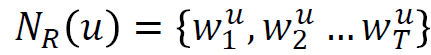
- 𝚫 size window에서 동시에 발생하는 walks를 예측하는 방법을 학습합니다.
- anonymous walk 의 𝒘 임베딩을 측정합니다.
- 모든 가능한 walk embeddings의 수가 입니다.
Objective:
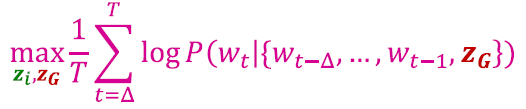

최적화 후에 그래프 임베딩 를 얻을 수 있습니다.
- 은 단순히 walk 임베딩 의 합계입니까? 아니면 가 옆의 잔여 임베딩입니까?
- 논문에 따르면 는 다른 과 마찬가지로 별도로 최적화된 벡터 매개변수입니다.
- 를 사용해서 예측합니다. (예: graph classification)
- Option1: Inner product kernel (Lecture2)
- Option2: 를 입력으로 사용하는 신경망을 사용해서 G를 분류합니다.
Overall Architecture
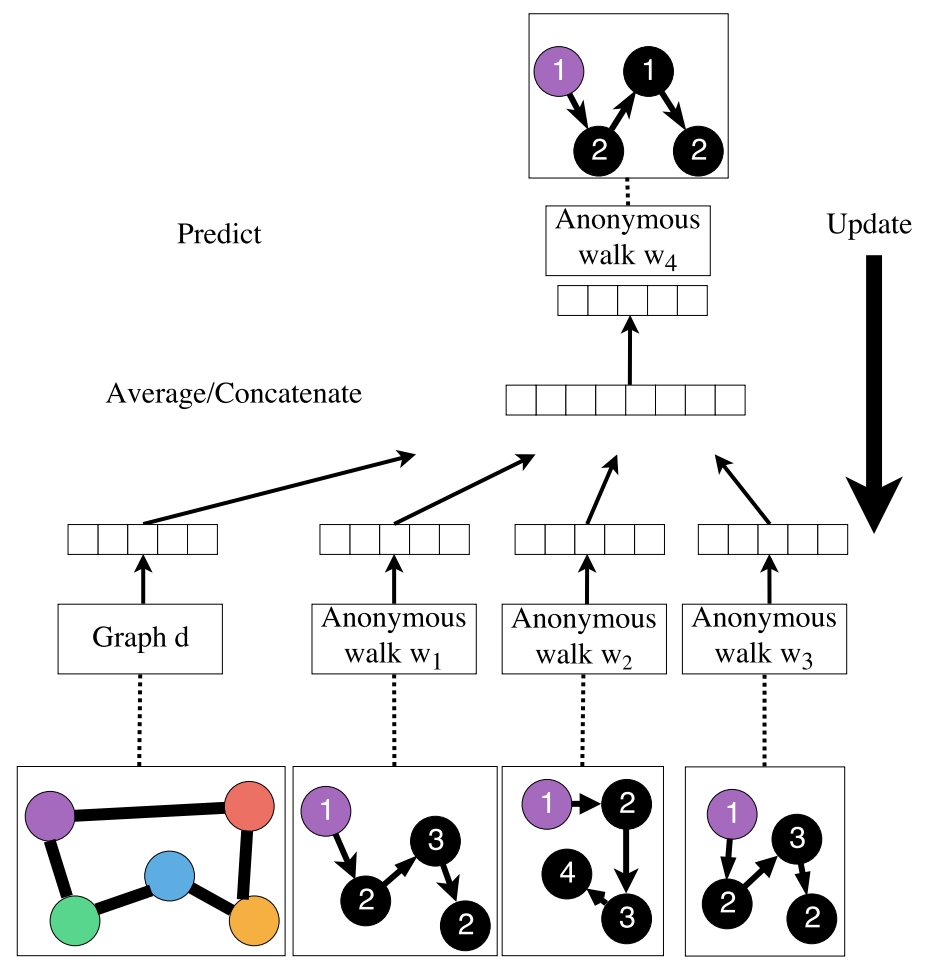
Summary
- 그래프 임베딩의 3가지 아이디어를 살펴보았습니다.
- Approach 1: 노드를 포함하고 합계/평균
- Approach 2: (하위) 그래프에 걸쳐 있는 슈퍼 노드를 생성한 다음 이를 포함
- Approach 3: Anonymous Walk Embeddings
- 아이디어 1: anon 샘플. 각 anon walk가 발생하는 시간의 일부로 그래프를 표시합니다.
- 아이디어 2: 익명 워크 임베딩과 함께 그래프 임베딩을 배웁니다.
Today’s Summary
feature engineering 없는 그래프 표현 학습, 다운스트림 작업에 대한 노드와 그래프 임베딩의 학습 방법에 대해 논의했습니다.
Encoder decoder framework:
- Encoder: embedding lookup
- Decoder: predict score based on embedding to match node similarity
Node similarity measure: measure:(biased) random walk
- Examples: DeepWalk , Node2Vec
Extension to Graph embedding: Node embedding aggregation and Anonymous Walk Embeddings
이상입니다. 감사합니다.
