Graph 강의 정리
강의 자료 출처: CS224W Lecture 5
Index
- Message Passing and Node Classification
- How do we leverage node correlations in networks
- Relational Classification
- Iterative Classification
- Collective Classification: Correct & Smooth
1. Message Passing and Node Classification
Outline
이번 강의의 개요는 일부 노드에만 라벨이 있는 네트워크가 주어졌을 때 네트워크에서 모든 다른 노드들에 라벨을 어떻게 맞게 배정하는지에 대해서입니다.
예를 들어, 네트워크에서 일부 노드가 fraudsters일 때, 다른 노드들은 전부 trusted입니다. 다른 fraudsters와 trustworthy 노드를 어떻게 찾습니까?
우리는 이미 Lecture3에서 풀 수 있는 3가지 노드 임베딩 방법을 논의하였습니다.
Example: Node Classification
일부만 라벨이 있는 노드가 주어졌을 때, 라벨이 없는 노드를 예측해 봅시다. 이것을 semi-supervised node classification이라고 부릅니다.
Message passing에 대해 배우게 될 것입니다.
- Intuition: Correlations(상관관계: dependencies 종속성)은 네트워크에 존재합니다.
- 다른 말로는 비슷한 노드끼리 연결되어 있다고 합니다.
- 주요 개념은 collective classification입니다. 네트워크의 모든 노드에 라벨을 부여하는 아이디어를 일컫습니다.
- 우리는 세 가지 테크닉을 보게 될 것입니다.
- Relational classification
- Iterative classification
- Correct & Smooth
Correlations Exist in Networks
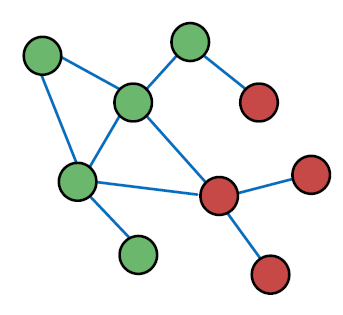
- 노드의 동작은 네트워크의 링크 전체에서 상관 관계가 있습니다.
- Correlation(상관 관계): 인접 노드는 동일한 색상을 가집니다. (동일한 클래스에 속함)
- 왜 노드의 동작이 네트워크에서 상관관계가 있는지 두 갈래로 설명할 수 있습니다.
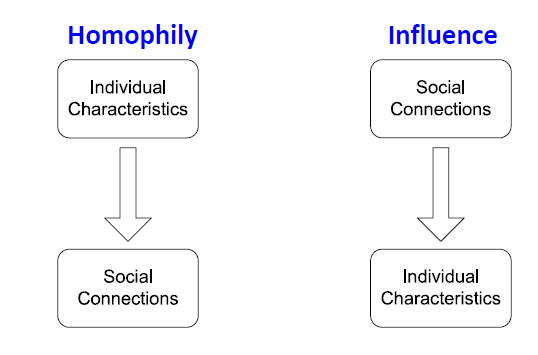
Social Homophily
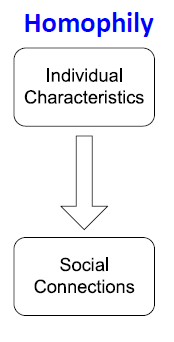
- Homophily: 개인이 유사한 다른 사람들과 연합하고 결속하려는 경향을 뜻합니다.
- “Birds of a feather flock together” (유유상종)
- 다양한 속성에 기반해서 네트워크 연구의 방대한 배열에서 관찰되어 왔습니다.
- 예: 같은 연구 분야에 집중하는 연구자들은 connection을 설립합니다. (예를 들어 콘퍼런스에서의 미팅, 학술제 등)
Homophily: Example

- 온라인 소셜 네트워크
- Nodes = people
- Edges = friendship
- Node color = interests (sports, arts, etc.)
- 같은 흥미를 가진 사람들은 homophily 때문에 가깝게 연결됩니다.
Social Influence: Example
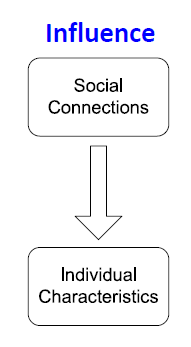
- Influence: 사회적 연결은 사람들의 개별 성격에 영향을 줍니다.
- 예를 들어, 저는 제 친구들에게 제가 가장 좋아하는 장르의 음악을 한 명이라도 좋아할 때까지 저의 음악적 성향을 추천할 수 있습니다.
2. How do we leverage node correlations in networks
Classification with Network Data
노드 라벨을 예측하는데 도움을 주기 위해 네트워크에서 관찰된 상관관계는 어떻게 영향력을 줄 수 있습니까?
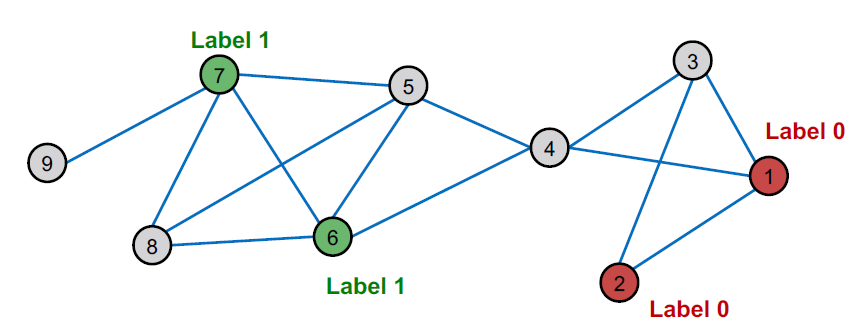
위 이미지에서 회색깔 노드의 라벨을 어떻게 예측할 수 있습니까?
Motivation (1)
비슷한 노드는 전형적으로 서로 가깝거나 네트워크에서 직접적으로 연결됩니다.
- Guilt-by-association: 레이블이 𝑋인 노드에 연결되어 있으면 레이블도 𝑋일 가능성이 높습니다.
- Example: 악성/양성 웹 페이지의 경우, 악성 웹 페이지는 서로 연결되어 가시성을 높이고, 신뢰할 수 있게 보이고, 검색 엔진에서 더 높은 순위를 차지합니다.
Motivation (2)
네트워크에서 노드 의 라벨 분류는 아래에 의존합니다.
- 의 Features
- 의 이웃에 있는 노드의 Label
- 의 이웃에 있는 노드의 Features
Semi-supervised Learning (1)
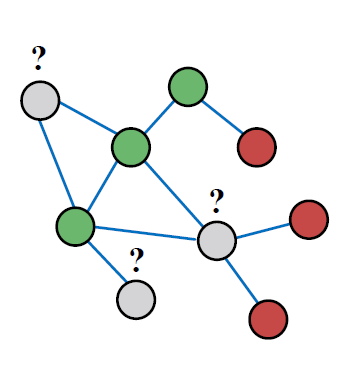
기본 세팅
Given
- 그래프
- 일부 라벨이 있는 노드
Find
- 남아 있는 노드들의 Class (red/green)
Main assumption
- 네트워크의 homophily가 있다
Semi-supervised Learning (2)
Task의 예
- 개의 노드를 갖는 의 인접 행렬
- Labels의 벡터
- Class 1에 속하면
- class 0에 속하면 라
- 라벨이 없는 노드들은 분류가 필요함
- Goal: 라벨이 없는 노드의 Class를 예측하는 것
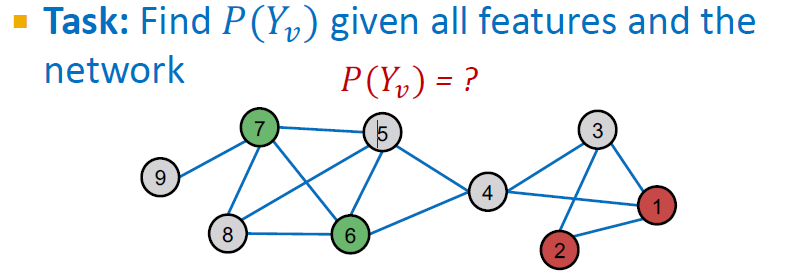
Problem Setting
의 unlabeled nodes의 라벨 를 어떻게 예측할 것인지?
- 각 노드 는 feature vector 를 가짐
- 일부 노드의 라벨은 초록일 경우 1, 빨강일 경우 0으로 주어짐
- Task: 모든 feature와 network가 주어질 때 를 찾는 것
Example applications:
이 설정에서 많은 응용 프로그램이 존재합니다.
- Document classification
- Part of speech tagging
- Link prediction
- Optical character recognition
- Image/3D data segmentation
- Entity resolution in sensor networks
- Spam and fraud detection
Overview of What is Coming
우리는 semi-supervised 바이너리 노드 분류에 중점을 둡니다.
세 가지 접근법을 소개합니다.
- Relational classification
- Iterative classification
- Correct & Smooth
3. Relational Classification
Probabilistic Relational Classifier (1)
- 아이디어: 네트워크 전체에 노드 레이블 전파
- 노드의 클래스 확률 은 이웃 클래스 확률의 가중 평균입니다.
- 레이블이 지정된 노드 𝑣의 경우 ground-truth label 을 사용하여 레이블 을 초기화합니다.
- 레이블이 지정되지 않은 노드의 경우 로 초기화합니다.
- 수렴 또는 최대 반복 횟수에 도달할 때까지 모든 노드를 무작위 순서로 업데이트합니다.
Probabilistic Relational Classifier (2)
각 노드 , 라벨 (예를 들면, 0 또는 1)을 업데이트합니다.
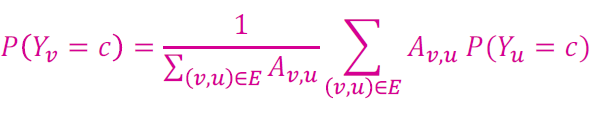
만약 엣지가 strength/weight information을 갖고 있다면, 는 와 사이의 엣지 가중치가 될 수 있습니다.
는 라벨 를 갖는 노드 의 확률입니다.
Challenges:
- 수렴이 보장되지 않습니다.
- 모델은 노드의 feature 정보를 사용합니다.
Example: Initialization
Initialization:
- 라벨이 있는 모든 라벨 노드
- 라벨이 없는 노드 0.5 (class 1에 속할 확률이 0.5)
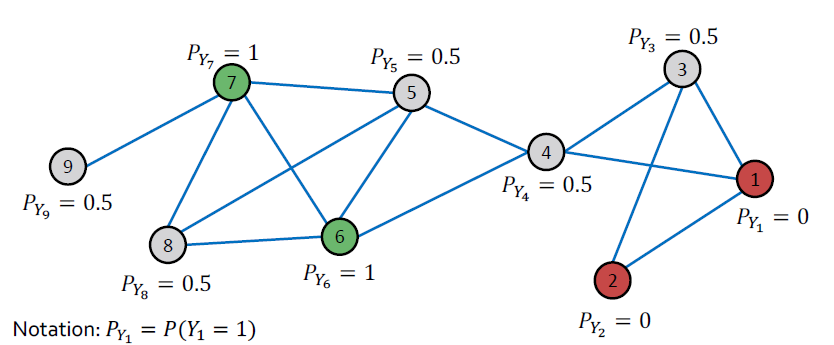
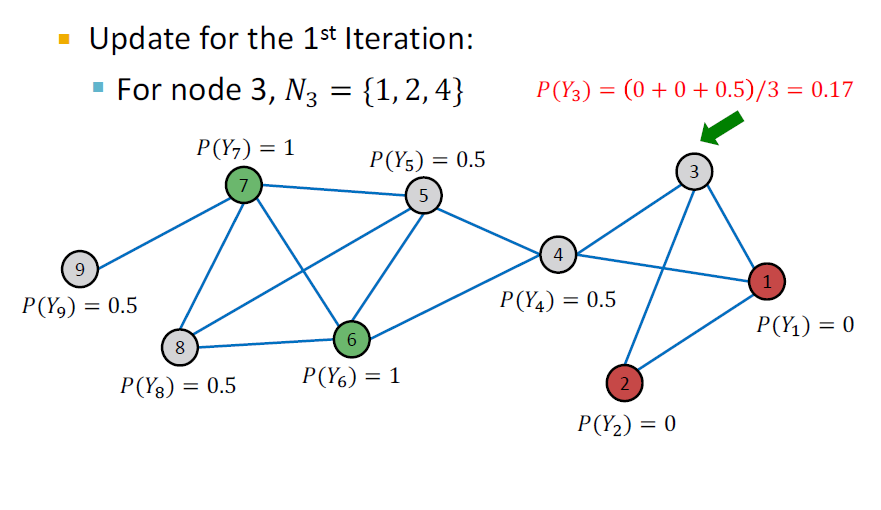
Example: Initialization, Update Node 3
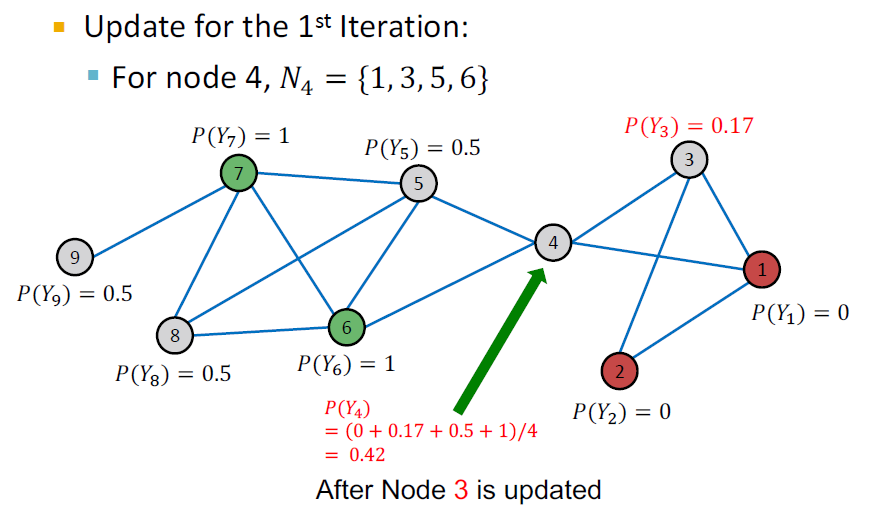
Example: Initialization, Update Node 4
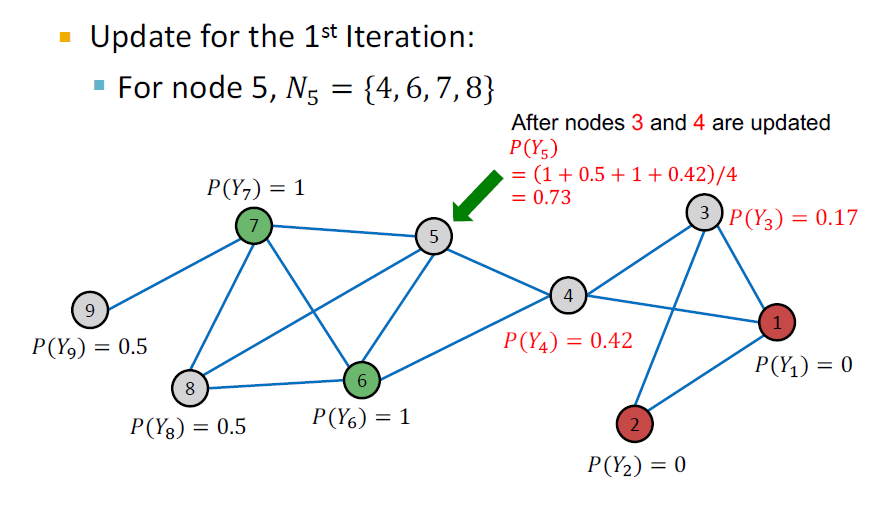
Example: Initialization, Update Node 5
Example: After Iteration
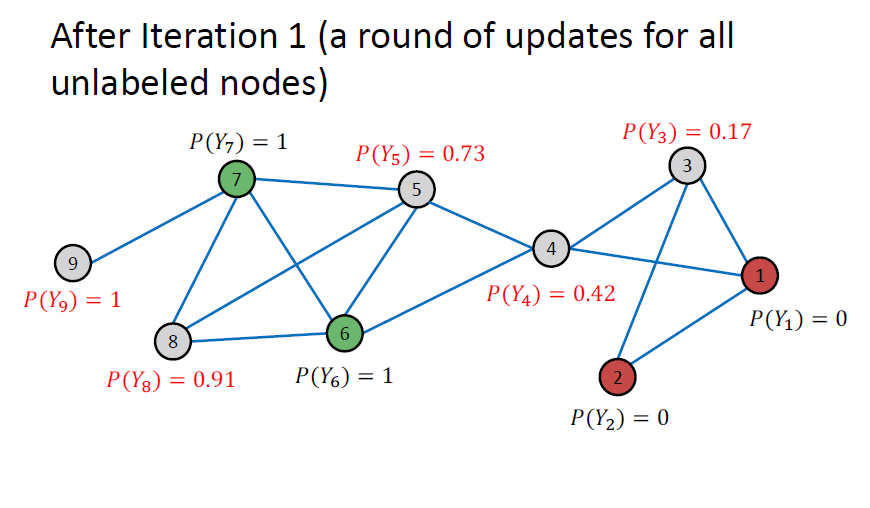
Example: After Iteration
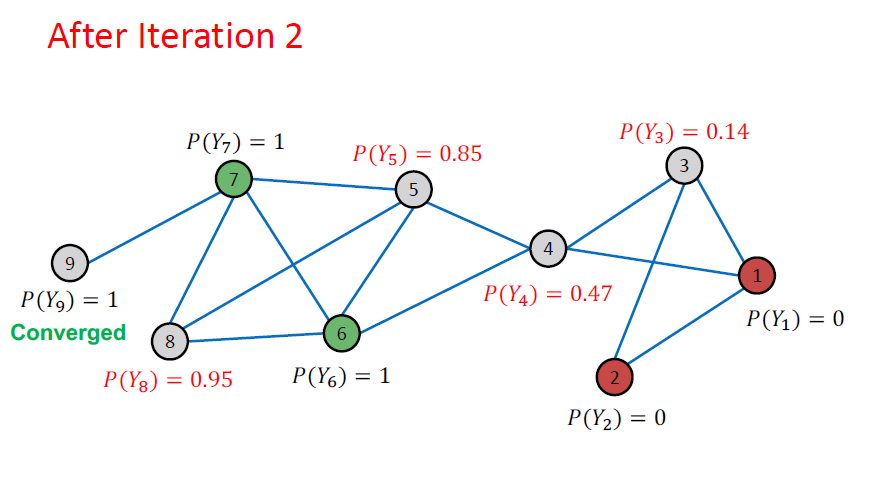
Example: After Iteration
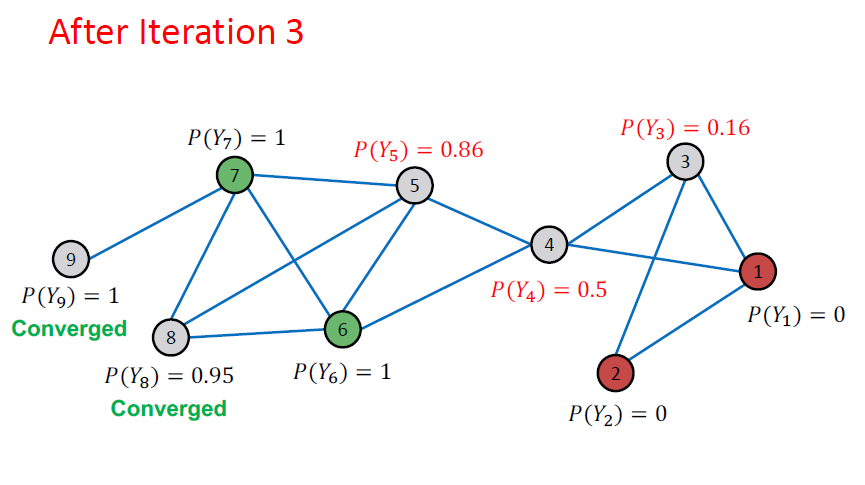
Example: After Iteration
하나씩 살펴보면 계속 반복하면서 업데이트 과정을 거친다는 것을 알 수 있습니다.
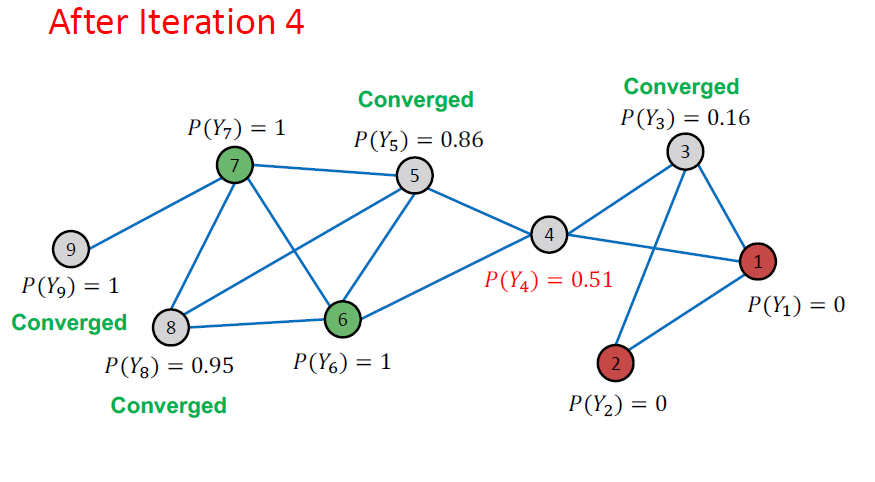
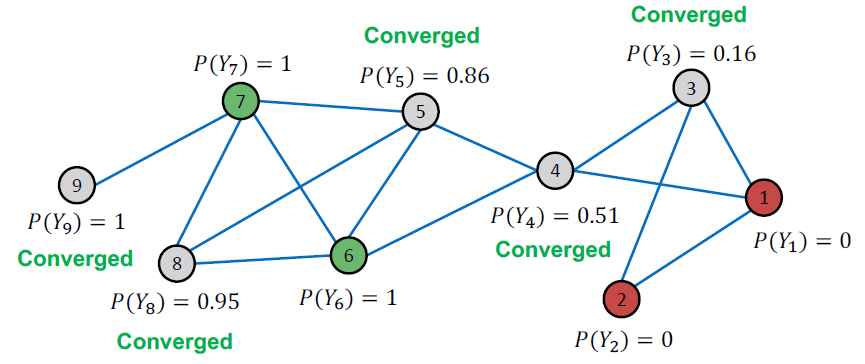
Example: Convergence
모든 점수는 4번 반복 이후 이후 수렴됩니다. 따라서 우리는 다음과 같이 예측합니다.
- 노드 4, 5, 8, 9는 class 1에 속한다 ()
- 노드 3은 class 0에 속한다 ()
4. Iterative Classification
Iterative Classification
-
관계형 분류자는 노드 속성을 사용하지 않습니다.
-
어떻게 활용할 수 있습니까?
-
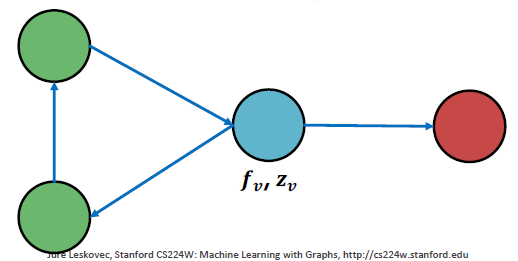
반복적 분류의 주요 아이디어: 이웃 집합 의 레이블 뿐만 아니라 속성 을 기반으로 노드 를 분류합니다.
-
입력: 그래프
- : 노드 의 feature vector
- 일부 노드 는 로 분류됩니다.
-
작업: 라벨 없는 노드들의 라벨 예측
-
두 가지 분류기로 학습하는 접근 방법
- base classifer / 노드 featur vector 에 기반해서 노드 라벨을 예측합니다.
- relational classifier / 노드 featur vector 와 의 이웃 라벨의 요약 에 기반해서 라벨을 예측합니다.
Computing the Summary
의 이웃 의 라벨의 요약 를 어떻게 계산합니까?
- = 노드 의 주위에서 label을 capture하는 벡터입니다.
- 에서 각 라벨의 숫자 히스토그램
- 에서 대부분의 라벨
- 에서 다른 라벨의 수
Architecture of Iterative Classifiers
Phase 1: Classify based on node attributes alone
라벨이 있는 훈련 세트에서 두 가지 분류기를 학습합니다. 아까 나온 Base classifier와 Relational classifier입니다.
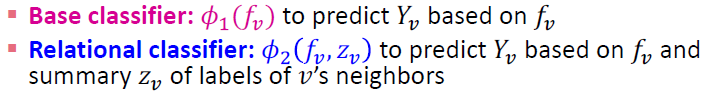
Phase 2: Iterate till convergence
- 테스트 세트에서 분류기 에 기반한 라벨 을 설정하고 를 계산한 뒤 로 라벨을 예측합니다.
- 각 노드 를 반복합니다.

- 클래스 라벨이 안정되거나 반복이 최대 수로 도달할 때까지 반복합니다.
- *Note: 수렴이 보장되지 않음*
Example: Web Page Claasification (1)
- Input: Graph of web pages
- Node: Web page
- Edge: Hyper-link between web pages
- Directed edge: a page points to another page
- Node features: Webpage description
- For simplicity, we only consider two binary features
- Task: Predict the topic of the webpage
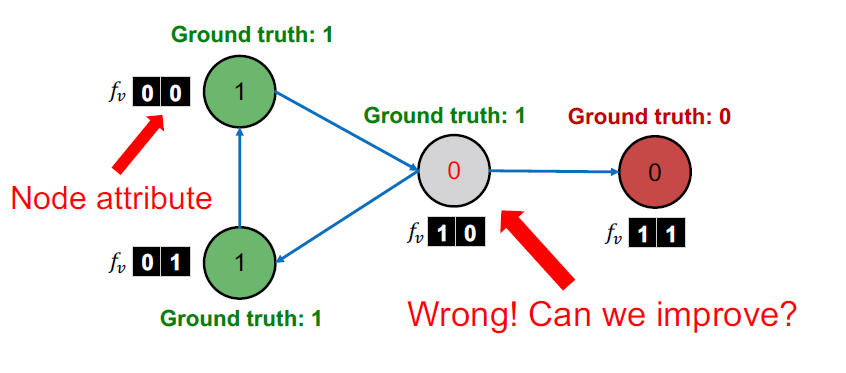
Example: Web Page Claasification (2)
- Baseline: Train a classifier (e.g., linear classifier) to classify pages based on node attributes.
Example: Web Page Claasification (3)
각 노드는 이웃 라벨의 벡터 를 유지합니다.
- = 들어오는 이웃 레이블 정보 벡터
- = 나가는 이웃 레이블 정보 벡터
- 만약 들어오는 페이지 중 최소 하나의 라벨이 0이라면 이다. 다른 정의도 비슷합니다.
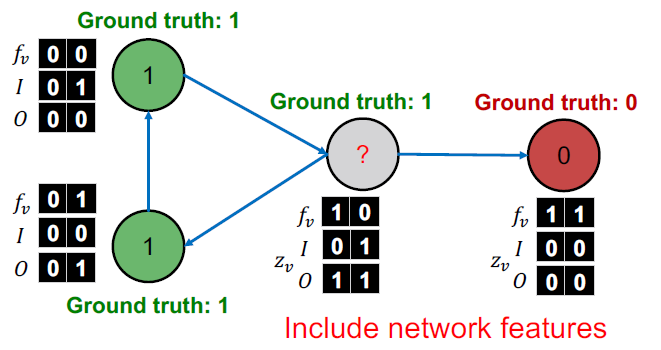
Iterative Claasifier - Step 1
= 1. Train classifiers
학습 레이블에서 두 가지 분류기를 학습합니다.
- Node attribute vector only:
- Node attribute and link vector :
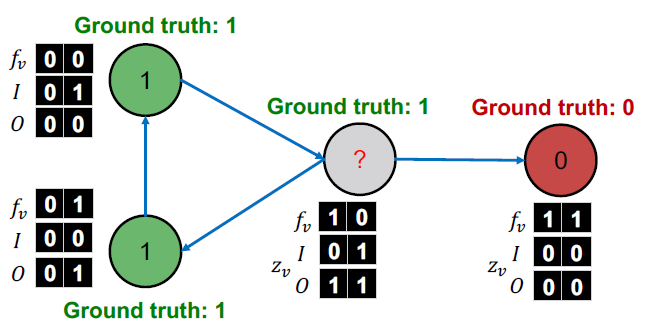
Iterative Claasifier - Step 2
= 2. Apply classifier to unlabeled set
라벨이 없는 세트에서, feature vector 분류기 를 로 설정합니다.
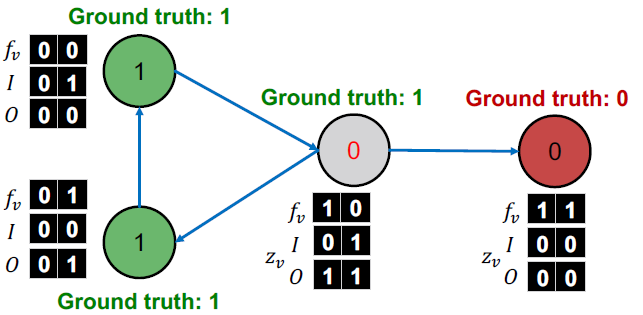
Iterative Claasifier - Step 3.1
= Iterate (4. Update relational features )
모든 라벨의 를 업데이트합니다.
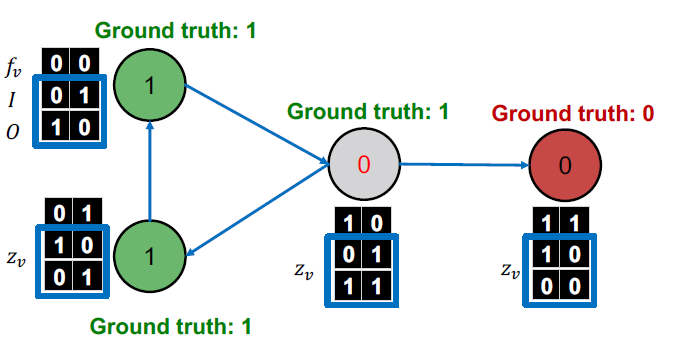
Iterative Claasifier - Step 3.2
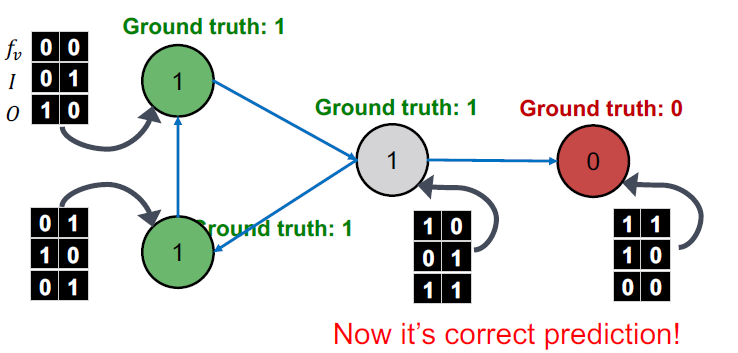
= Iterate (5. Update label )
로 모든 노드를 재분류합니다.
Iterative Claasifier - Iterate
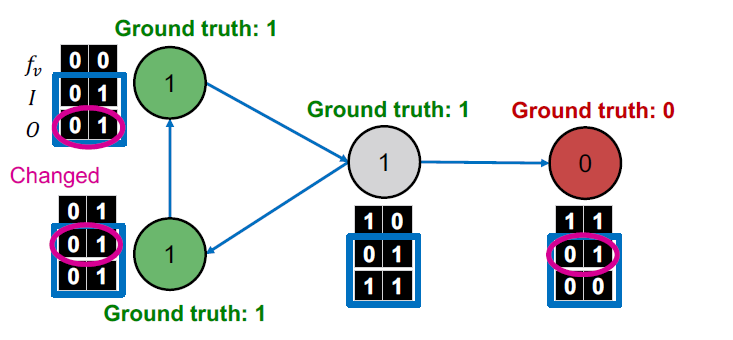
= Iterate
수렴할 때까지 반복합니다.
- 에 기반한 를 업데이트
- 를 업데이트
Iterative Claasifier - Final Prediction
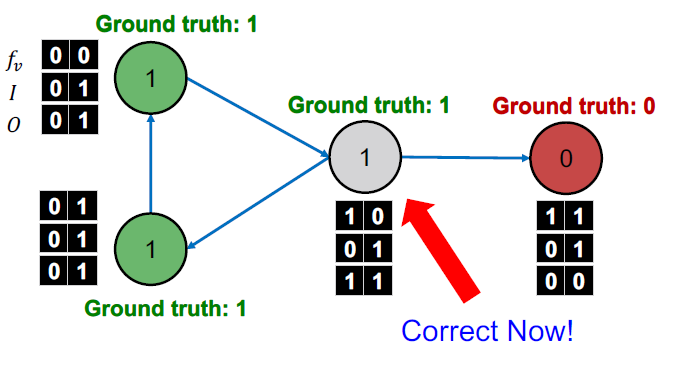
Stop iteration
- 수렴 후에 또는 반복 횟수가 최대로 도달했을 때 멈춥니다.
Summary
collective classification의 두 가지 접근법에 대해 얘기했습니다.
- Relational classification
- 이웃한 노드에 기반하여 라벨 클래스에 속하는 노드의 확률을 반복적으로 업데이트합니다.
- Iterative classification
- attribute/feature information을 다루면서 collective classification을 증진시킵니다.
- 이웃한 라벨과 그 features에 기반한 노드 를 분류합니다.
5. Collective Classification: Correct & Smooth
Correct & Smooth (C&S)
- 세팅: 노드에 대한 부분적으로 레이블이 지정된 graph 및 features
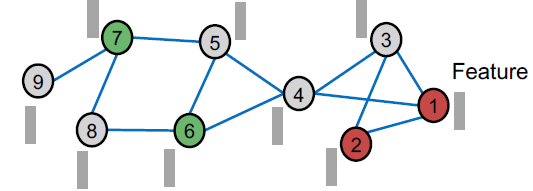
- Train base predictor
- Use the base predictor to predict soft labels of all nodes.
- Post-process the predictions using graph structure to obtain the final predictions of all nodes.
C&S(1) Train Base Predictor
(1) 모든 노드에 걸쳐 soft labels(클래스 확률)을 예측하는 base predictor을 학습시킵니다.
라벨이 있는 노드들은 학습과 검증 데이터에 사용되고 **base predictor**는 간단합니다. → 모든 feature에 대한 선형 모델과 MLP입니다.
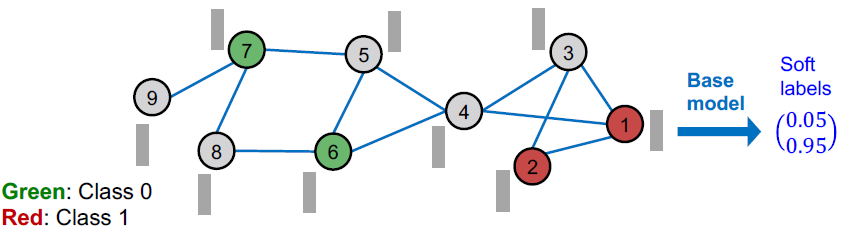
C&S(2) Predict Over All Nodes
(2) 학습한 base predictor가 주어졌을 때, 모든 노드에 대한 soft labels을 얻어서 적용할 수 있습니다.
- soft labels이 상당히 정확할 것이라고 기대합니다.
- 예측을 더 정확하게 만들기 위해 그래프 구조를 사용하여 예측을 후처리할 수 있습니까?
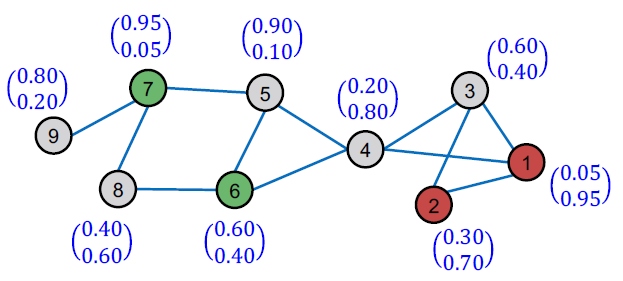
C&S(3) Post-Process Predictions
(3) C&S는 soft prediction을 후처리 하기 위해 두 가지 단계를 사용합니다.
- Correct step
- Smooth step
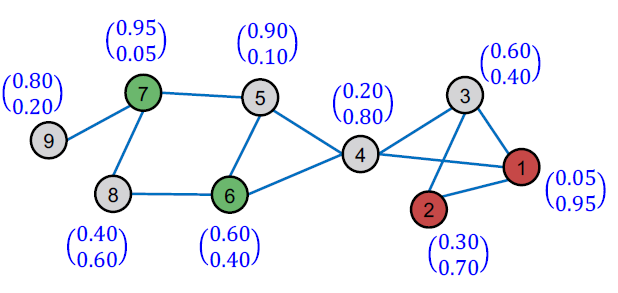
C&S Pose-Processing: Correct Step
핵심 아이디어는 기본 예측의 오류가 그래프의 가장자리를 따라 양의 상관 관계가 있을 것으로 예상한다는 것입니다. 즉, 노드 의 오류는 이웃 에서 유사한 오류가 발생할 가능성을 높입니다. 따라서 이러한 불확실성을 그래프 전체에 "확산"해야 합니다.
Intuition of Correct & Smooth
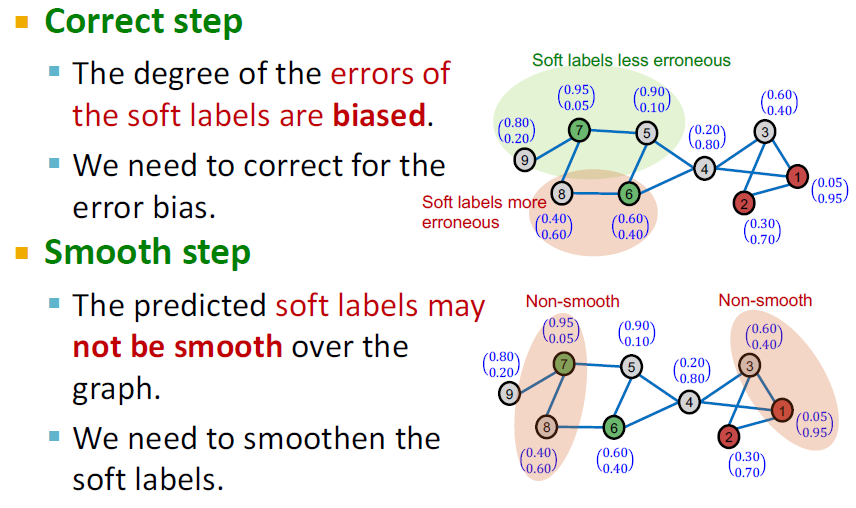
- Correct step
- 소프트 라벨의 오류 정도가 편향되어 있습니다.
- 오류 편향을 수정해야 합니다.
- Smooth step
- 예측된 소프트 레이블이 그래프에서 매끄럽지 않을 수 있습니다.
- 소프트 라벨을 부드럽게 해야 합니다.
C&S Pose-Processing: Correct Step(1)
- Correct step:
- 노드의 훈련 오류를 계산합니다.
- 훈련 오류: Ground-truth label에서 soft label을 뺍니다. 라벨이 없는 노드에 대해선 0으로 정의합니다.
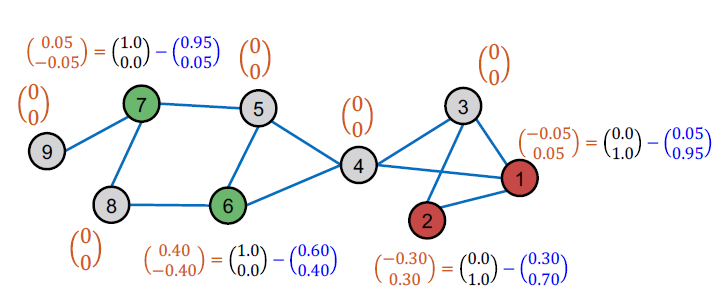
C&S Pose-Processing: Correct Step(2)
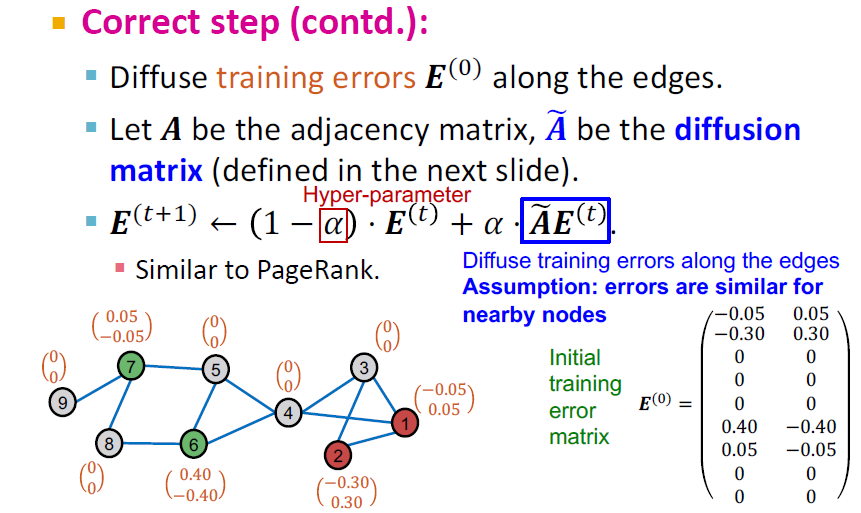
- 훈련 오류 를 엣지에 거쳐 확산시킵니다.
- 인접 행렬 A를 두고 가 디퓨전 행렬이 됩니다. (다음 슬라이드에서 정의 됩니다.)
- (는 하이퍼 파라미터입니다)
- 는 인근 노드에 대한 오류가 비슷하다는 가정에서 edege를 따라 훈련 오류를 확산시킵니다.
Diffusion Matrix
- Normalized diffusion matrix
- 셀프 루프에 인접행렬 A까지 더합니다 ()
- 는 degree matrix가 됩니다.
Theoretical Motivation for
- Normalized diffusion matrix
- 모든 eigenvalue 는 범위 [-1, 1]을 가집니다.
Proof:
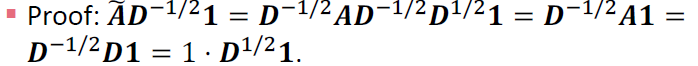
의 제곱은 어느 K에도 잘 적용됩니다.
- 의 eigenvalues는 항상 범위 [-1, 1]을 가집니다.
- 가장 큰 eigenvalue는 항상 1입니다.
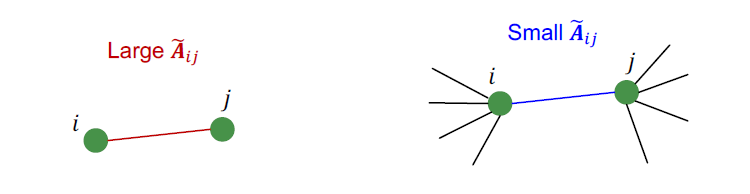
Intuition for
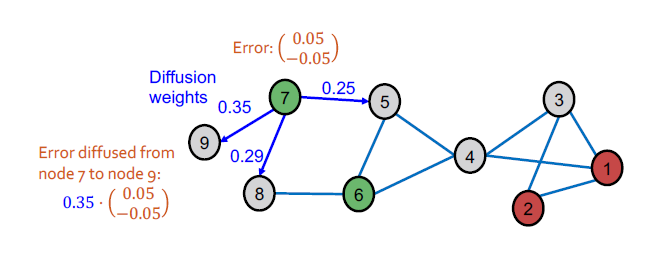
- 만약 와 가 연결되어 있다면, 가중치는 는 입니다.
- Intuition:
- Large: 와 가 각자 서로만 연결되어 있는 경우
- Small: 와 가 다른 여러 노드들과 함께 연결되어 있는 경우
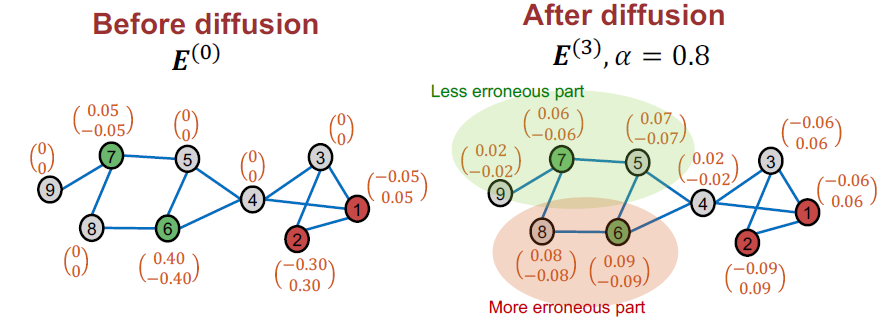
C&S Pose-Processing: Correct Step(3)
- Diffusion of training errors:
예측 오류가 근처 노드에 비슷하단 가정하에
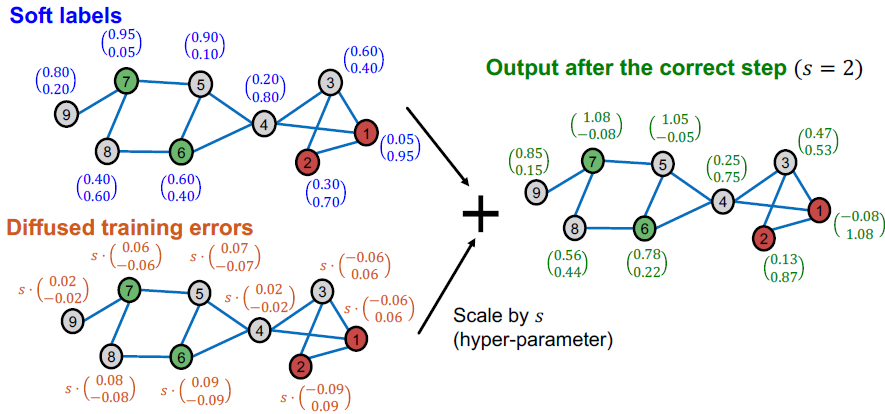
C&S Pose-Processing: Correct Step(4)
- 예측된 소프트 레이블에 확장된 diffused training errors를 추가합니다.
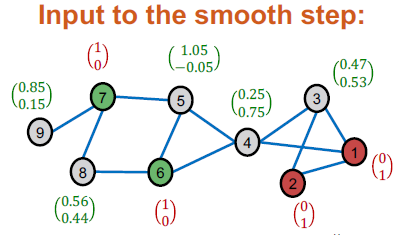
C&S Pose-Processing: Smooth Step
- 수정된 소프트 라벨을 가장자리를 따라 매끄럽게 만듭니다.
- 가정: 이웃 노드는 동일한 레이블을 공유하는 경향이 있습니다.
- 참고: 학습 노드의 경우 소프트 레이블 대신 ground-truth hard labels을 사용합니다.
C&S Pose-Processing: Smooth Step (1)
- Smooth step:
- 는 하이퍼 파라미터, 는 edge에 따른 확산된 라벨
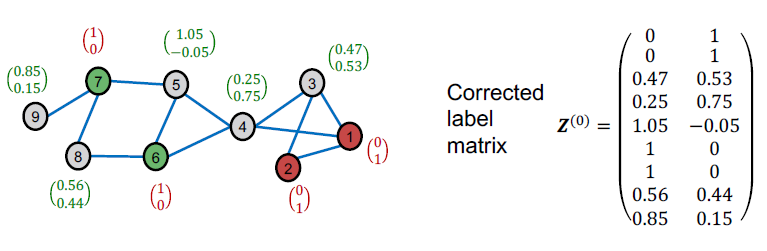
C&S Pose-Processing: Smooth Step (2)
C&S의 최종 클래스 예측은 최대 점수를 가진 클래스입니다.
참고: 점수는 직접적인 확률적 해석이 없지만(예: 각 노드에 대해 합계가 1이 아님) 점수가 클수록 클래스가 더 가능성이 있음을 나타냅니다.
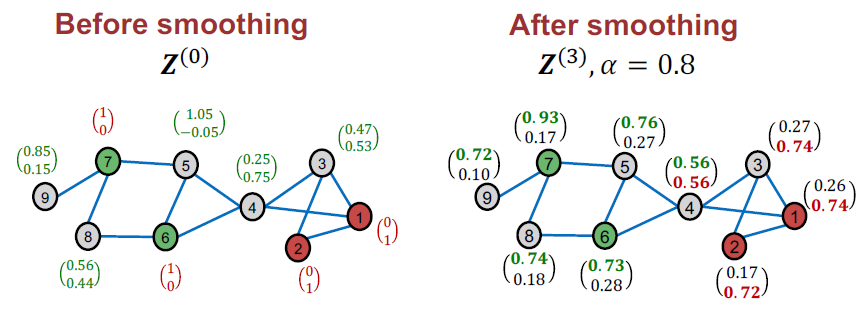
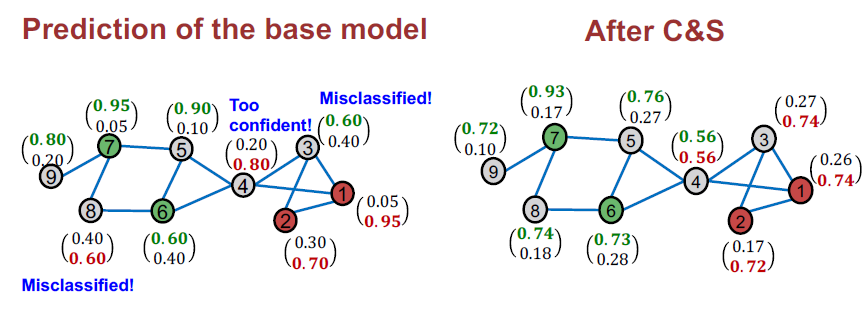
C&S: Toy Example Summary
C&S가 그래프 구조를 사용하여 기본 모델 성능을 성공적으로 개선했음을 보여줍니다.
C&S on a Real-World Dataset
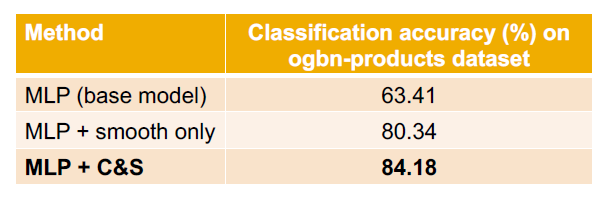
- C&S는 기본 모델(MLP)의 성능을 크게 향상시킵니다.
- C&S는 Smooth-only(올바른 단계 없음) baseline을 능가합니다.
Correct & Smooth: Summary
- C&S(Correct & Smooth)는 그래프 구조를 사용하여 기본 모델에서 예측한 소프트 노드 레이블을 후처리합니다.
- Correction step: 기본 예측자의 학습 오류를 확산 및 수정합니다.
- Smooth step: 기본 예측자의 예측을 부드럽게 합니다.
- C&S는 semisupervised 노드 분류에서 강력한 성능을 달성합니다.
Summary
우리는 노드에 대한 예측을 위한 그래프에서 상관 관계를 활용하는 방법을 배웠습니다.
핵심 기술:
- Relational classification
- Iterative classification
- Correct & Smooth
