강의 자료 출처: CS224W Lecture6

Recap: Node Embeddings

노드 임베딩은 Lecture 3에서 다뤘던 내용입니다.

노드를 d-차원 임베딩으로 매핑합니다. 이는 그래프에서 비슷한 노드들이 서로 가깝게 임베딩 된다는 걸 의미합니다.

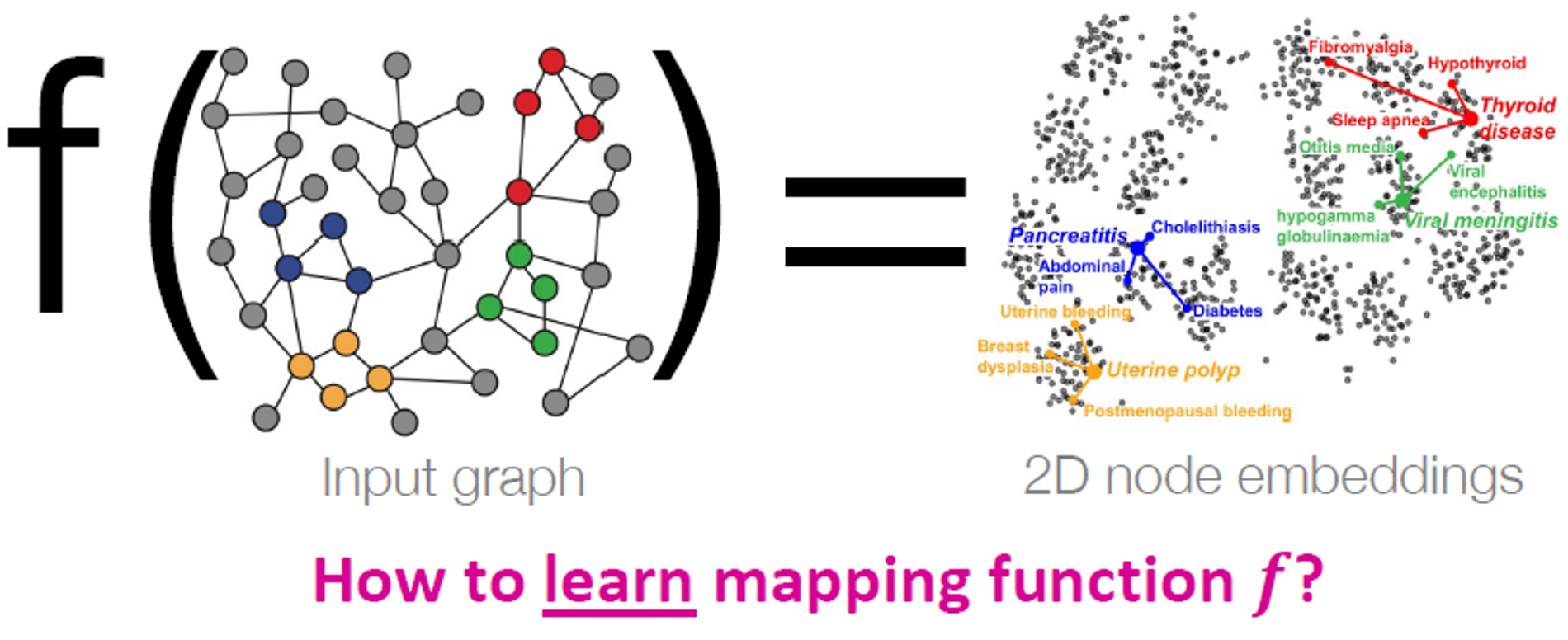
목표는 노드 $u,v$의 유사도를 계산하는 것이었고, 이를 정의내리기 위해 $ENC(u), ENC(v)$를 계산했습니다.

$ENC(v) = z_v$

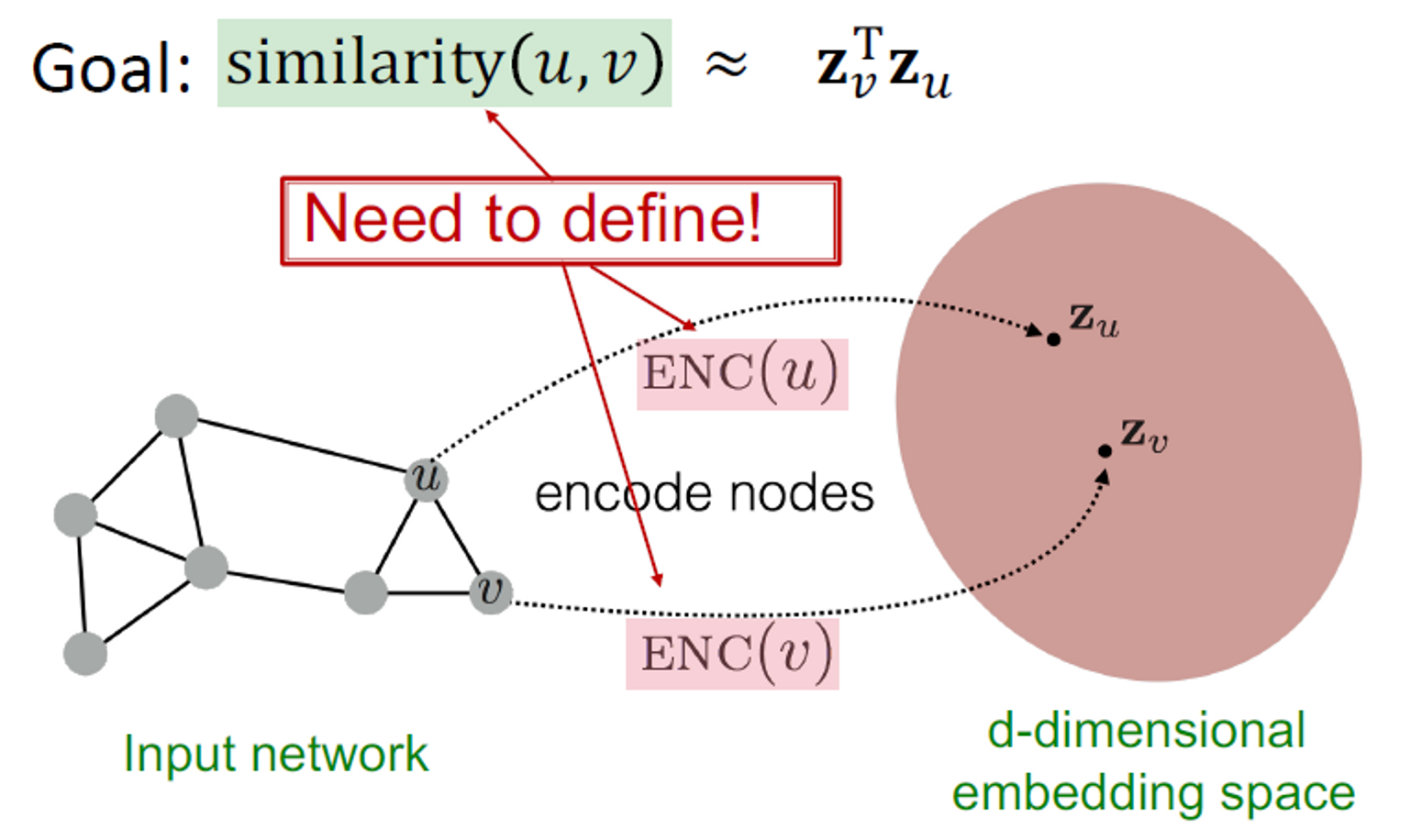
Encoder는 각 노드를 낮은 차원의 벡터로 매핑합니다. $v$는 입력 그래프의 노드입니다. $z_v$는 d차원의 임베딩입니다.

유사도 함수는 벡터 공간의 관계가 원래 네트워크의 관계에 매핑되는 방식을 지정합니다.

$similarity(u, v) \approx z_v^T z_u$

Decoder는 원래 네트워크에서 $u$와 $v$ 사이의 유사도를 계산해주며, 노드 임베딩 사이의 내적을 계산합니다.

가장 간단한 인코딩 접근은 embedding-lookup입니다. 그림으로 이해할 수 있습니다.

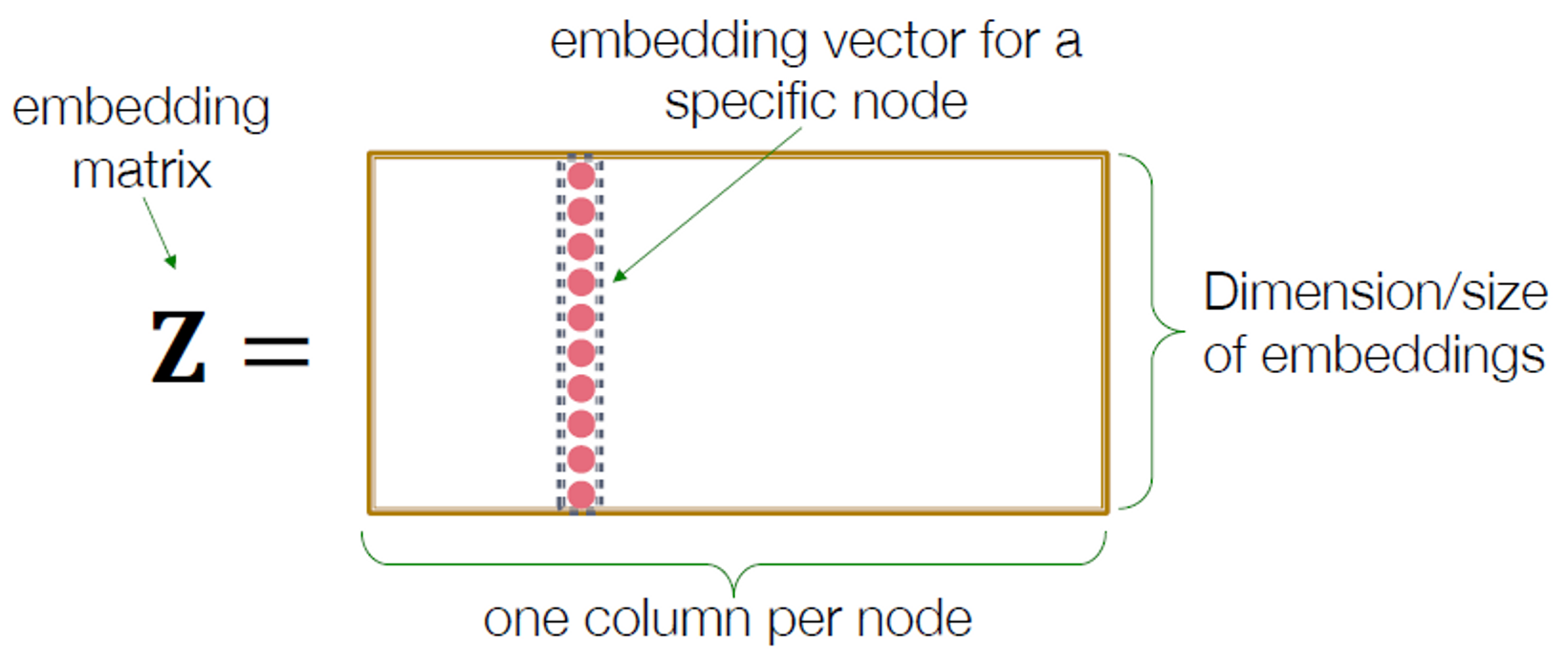
이런 얕은 임베딩 방법의 한계점

• $O(|V|)$ 파라미터가 필요합니다.
  • 노드 사이의 파라미터가 공유되지 않습니다.
  • 모든 노드는 각자의 임베딩을 갖고 있습니다.
• 본질적으로 “transductive” 합니다.
  • 훈련 동안 보이지 않는 노드의 임베딩을 생성하지 않습니다.
• 노드 features을 통합하면 안됩니다.
  • 많은 그래프의 노드에는 활용할 수 있고 활용해야 하는 features가 있습니다.

Today: Deep Graph Encoders

이번 차시에서는 graph neural networks에 기반이 되는 딥러닝 방법에 대해 얘기하게 될 것입니다. → GNN

모든 깊은 인코딩은 노드 유사성 함수와 결합될 수 있습니다. (Lecture 3에서 언급함)

Deep Graph Encoders

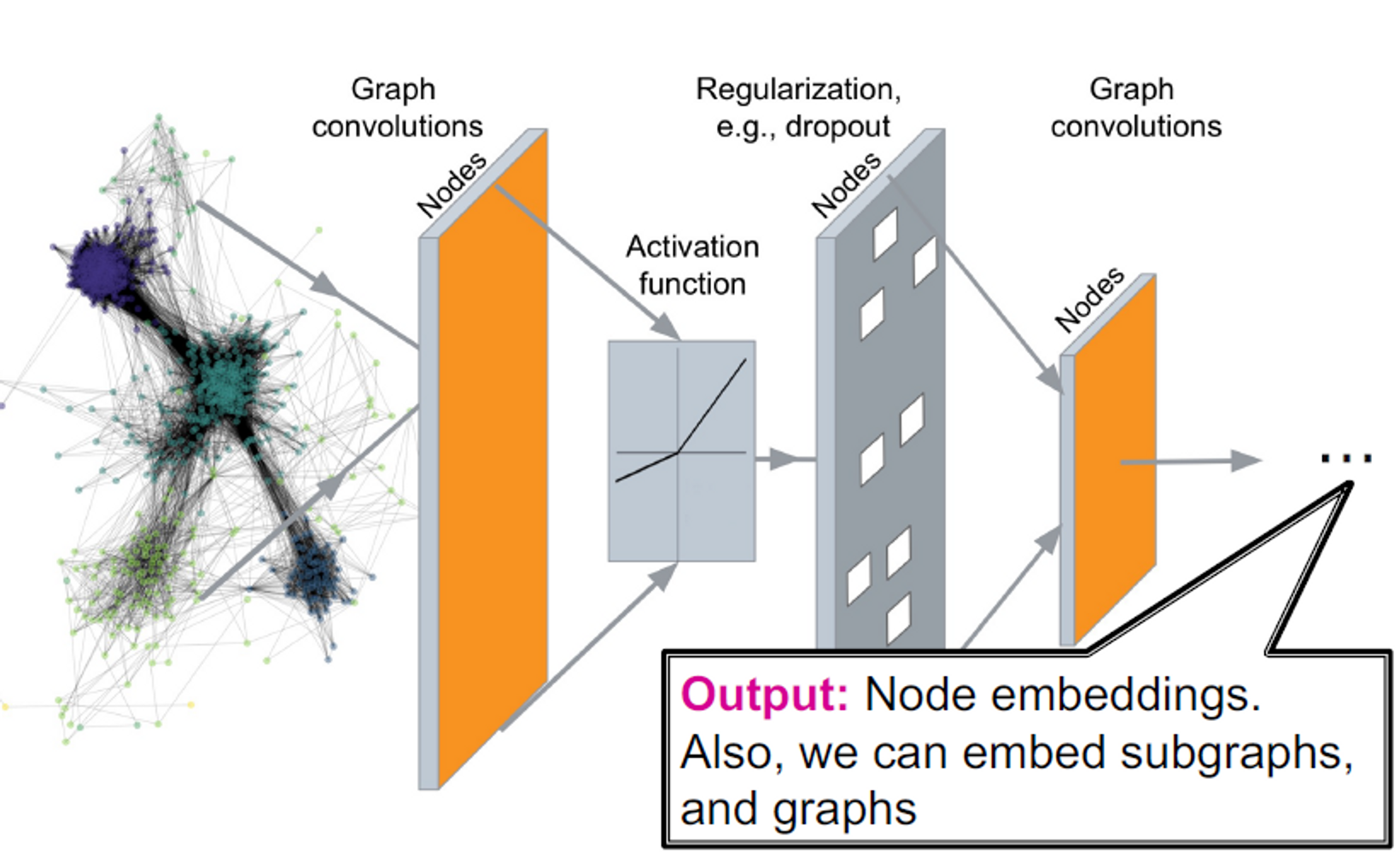
Task on Networks

우리가 풀게 될 작업들

• Node classification
  • Predict a type of a given node
• Link prediction
  • Predict whether two nodes are linked
• Community detection
  • Identify densely linked clusters of nodes
• Network similarity
  • How similar are two (sub)networks

현재 머신러닝의 도구들은 시퀀스나 그리드로 간단히 표현됩니다. 이것이 어려운 이유는 무엇일까요? 네트워크는 생각보다 복잡하기 때문인데요.

임의의 크기와 복잡한 토폴로지 구조를 가집니다. 즉, 그리드와 같은 공간적 지역성이 없습니다.

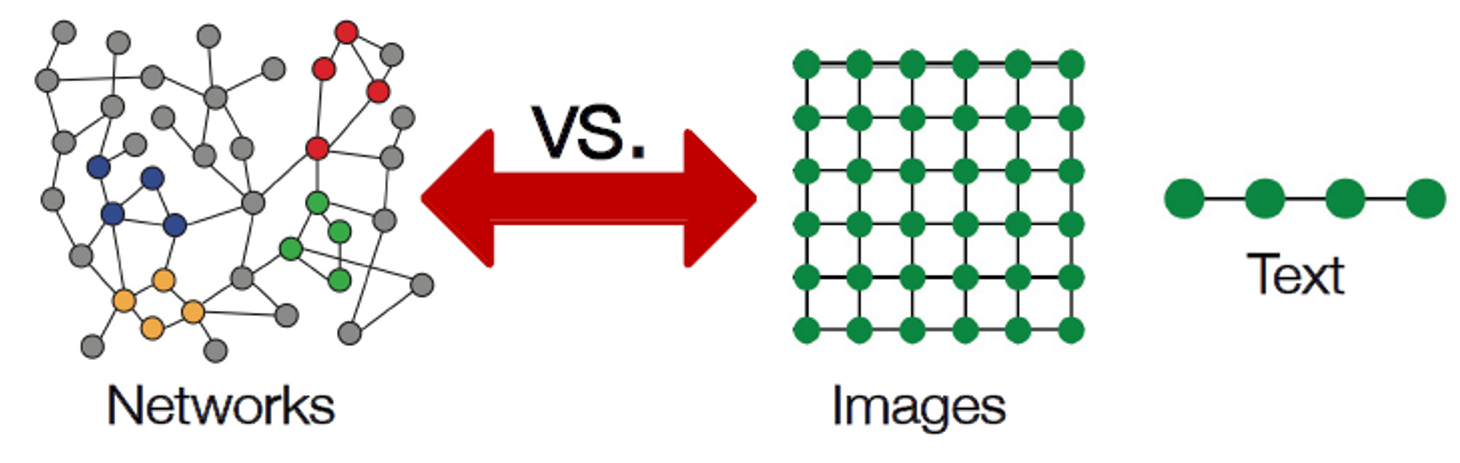
노드는 순서가 없고 참조 포인트로 고정되지 않습니다. 종종 역동적이고 multimodal features를 가집니다.

이번 강의의 개요입니다.

Index

1. Basics of deep learning
2. Deep learning for graphs
3. Graph Convolutional Networks
4. GNN subsume CNNs and Transformers

1. Basics of deep learning

강의를 좀 빠르게 훑어봐야 해서 딥러닝의 기본 개념은 강의 자료를 참고 부탁드립니다. 요약 부분만 정리하겠습니다.

• Objective function: $min_{\theta} L(y, f(x))$
• $f$ 는 간단한 선형 레이어로, MLP 또는 다른 신경망을 의미합니다.
• 입력값 $x$의 미니 배치 예입니다.
• Forward propagtaion: $x$가 주어졌을 때 $L$을 계산합니다.
• Back-propagation: 역전파를 사용해 미분값 $\nabla_w L$을 얻습니다.
• 매 반복마다 SGD(stochastic gradient descent)를 통해 $\theta$를 최적화합니다.

2. Deep learning for graphs

Content

• Local network neighborhoods:
  • Describe aggregation strategies
  • Define computation graphs
• Stacking multiple layers:
  • Describe the model, parameters, training
  • How to fit the model?
  • Simple example for unsupervised and supervised training

Setup

그래프 G를 갖고 있다고 가정합니다.

• $V$: vertex set
• $A$: adjacency matrix
• $X \in \mathbb{R}^{m \times |V|}$: node featues의 matrix
• $v$: $V$의 노드; $N(v)$: $v$의 이웃 집합
• Node features:
  • Social networks: User profile, User image
  • Biological networks: Gene expression profiles, gene functional information
  • When there is no node feature in the graph dataset:
    • Indicator vectors (one-hot encoding of a node)
    • Vector of constant 1: [1, 1, …, 1]

A Naive Approach

• Join adjacency matrix and featues
• DNN에 넣습니다.

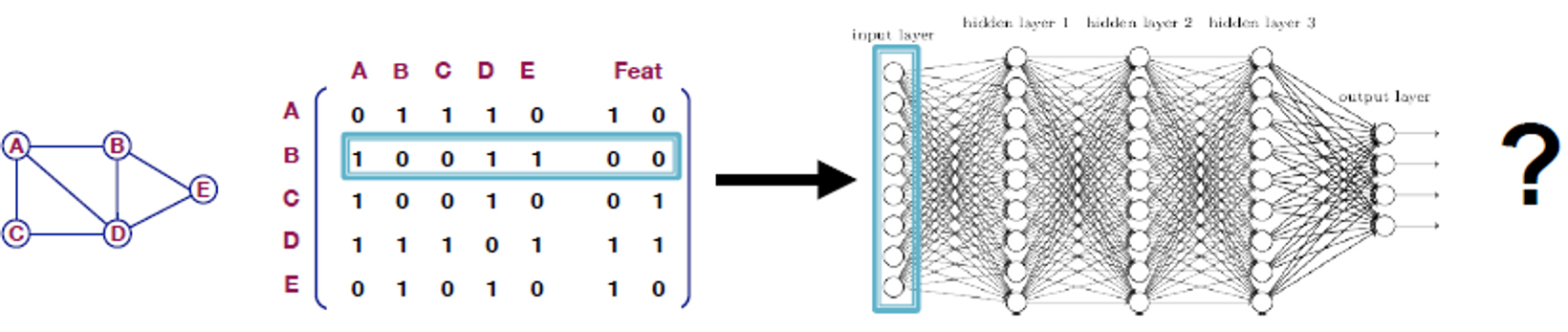
이 아이디어의 이슈

• $𝑂(|𝑉|)$ 파라미터
• 다른 사이즈의 그래프엔 적용 불가능
• 노드 순서에 민감함

Idea: Convolutional Networks

CNN on an image:

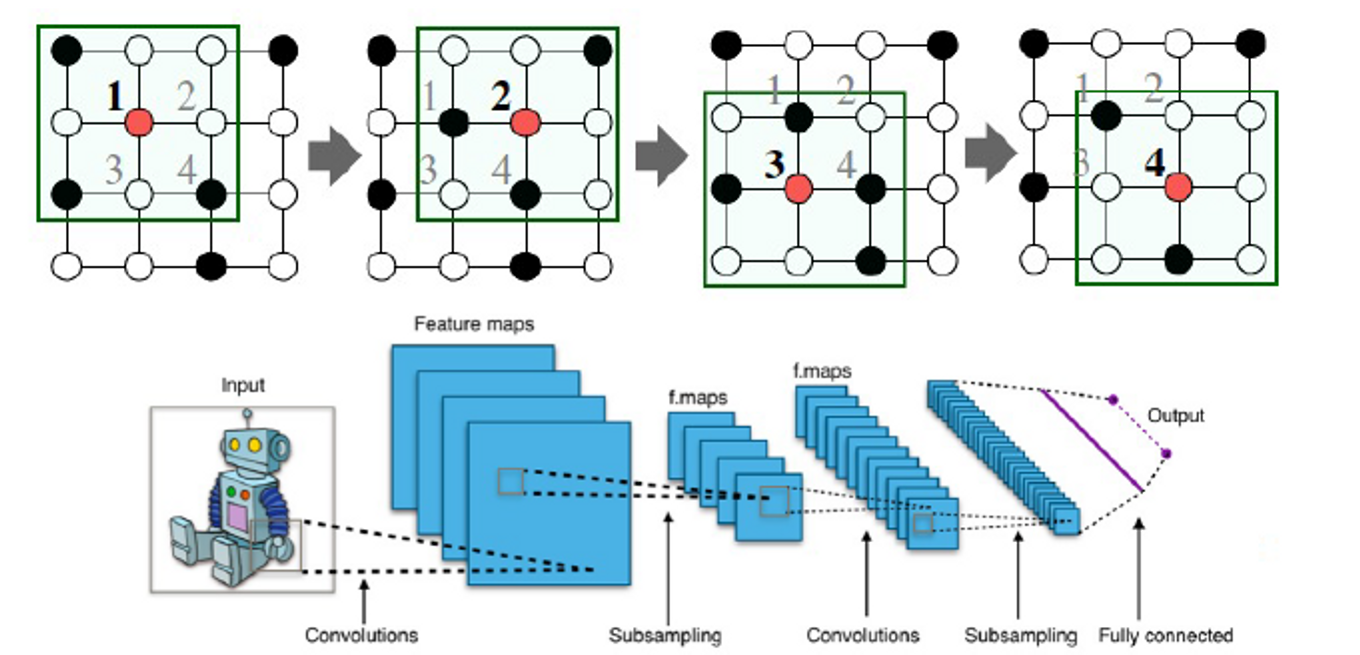
• 목표는 단순한 격자를 넘어 컨볼루션을 일반화하는 것입니다.
• 노드 기능/속성 활용(예: 텍스트, 이미지)

Real-World Graphs

그러나 그래프는 이렇게 생겼습니다.

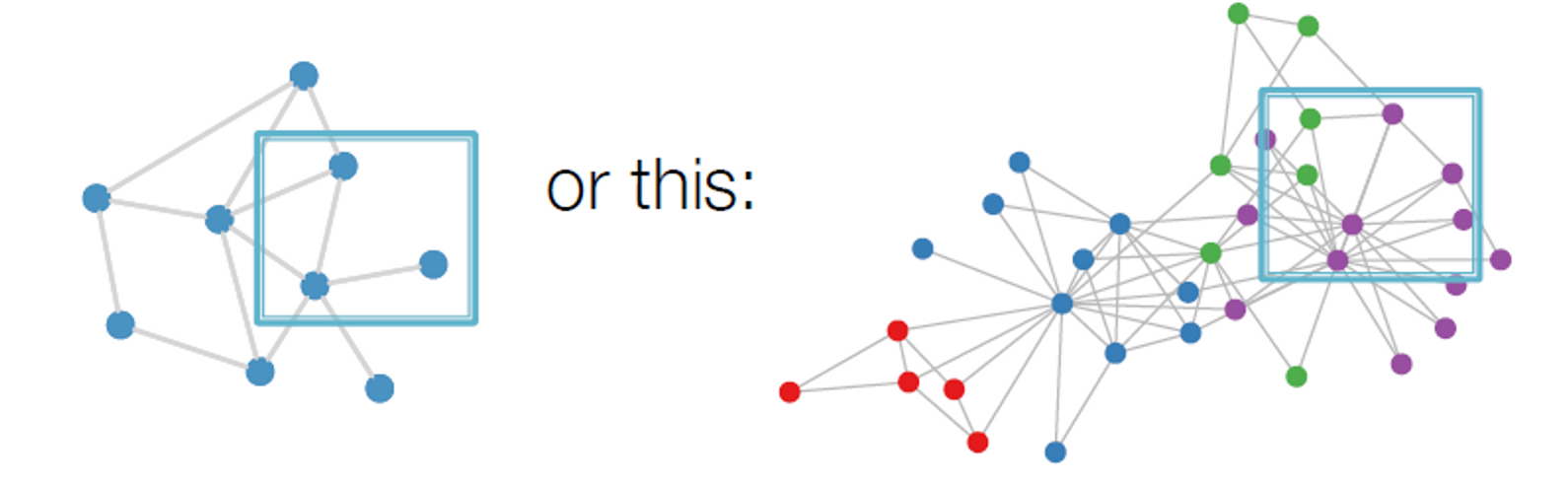
그래프에는 지역성 또는 슬라이딩 윈도우에 대한 고정된 개념이 없고, 그래프는 순열이 불변합니다.

Permutation Invariance

그래프에는 노드의 정식 순서가 없어서 다양한 순서 계획을 가질 수 있습니다.

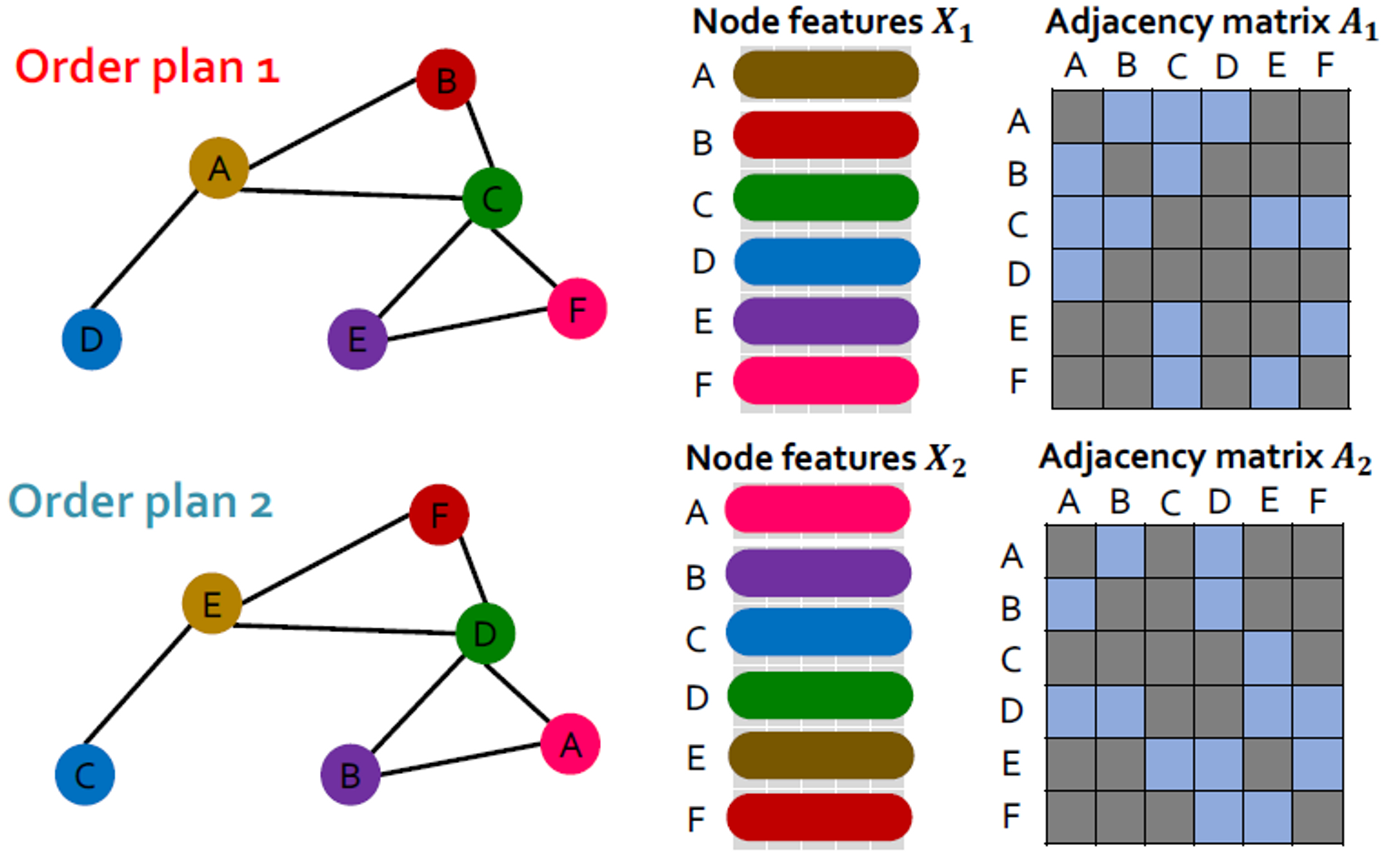
순서 계획 1과 순서 계획 2에 대해 그래프 및 노드 표현이 동일해야 합니다.

그래프 표현에서 두 순서 계획이 동일하다는 것은 어떤 의미인가요?

그래프 $G=(A,X)$가 벡터 $\mathbb{R}^d$로 매핑하는 함수 $f$를 학습하는 것을 고려할 수 있습니다.

$f(A_1, X_1) = f(A_2, X_2)$

• 𝑨는 인접행렬, 𝑿는 노드의 feature matrix입니다.

모든 순서 계획 $i, j$에 대해 $𝑓(𝑨_i,𝑿_i) = 𝑓(𝑨_j,𝑿_j)$라면, 공식적으로 $f$를 permutation invariant function이라고 말합니다. $m$ 노드를 가진 그래프에 대해 $m!$ 개의 다른 순서 계획이 있음을 뜻합니다.

Permutation Equivariance

Similarly for node representation:

그래프 $G$의 노드가 벡터 $\mathbb{R}^{m\times d}$로 매핑하는 함수 $f$를 학습합니다.

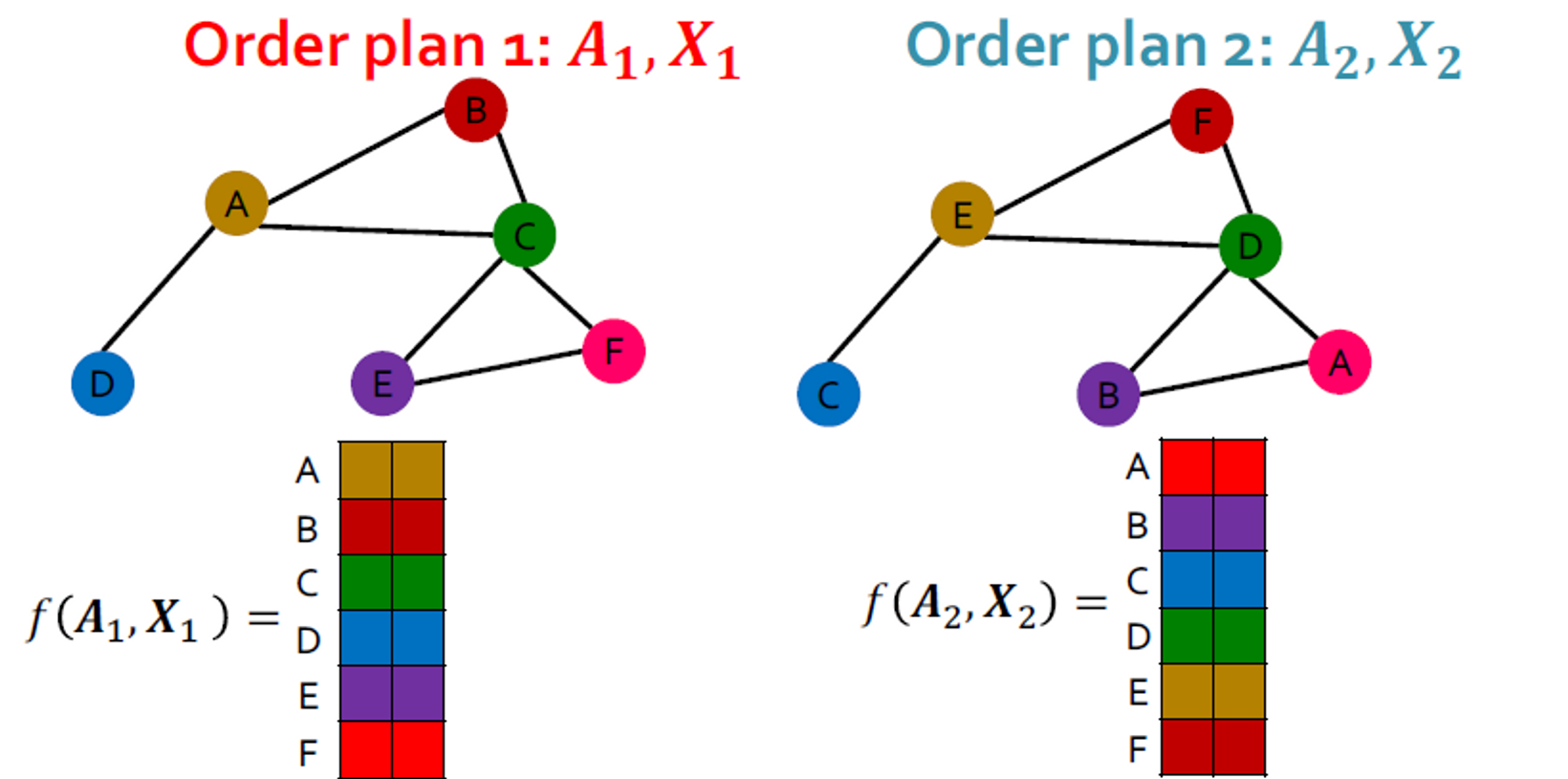
• 갈색 노드 A의 표현 벡터
• 갈색 노드 E의 표현 벡터
• 두 순서 계획에 대해, 같은 포지션의 노드 벡터들은 같습니다.

• 초록색 노드 C의 표현 벡터
• 초록색 노드 D의 표현 벡터
• 두 순서 계획에 대해, 같은 포지션의 노드 벡터들은 같습니다.

For node representation

그래프 $G$의 노드가 벡터 $\mathbb{R}^{m\times d}$로 매핑하는 함수 $f$를 학습하는 것을 생각합니다. 그래프는 $m$개의 노드를 갖고 있고, 각 행은 노드의 임베딩으로 볼 수 있습니다.

비슷하게, 이 속성이 순서 계획 $i, j$의 쌍에 유지되는 경우 $f$를 permutation equivariant function이라 합니다.

Graph Neural Network Overview

그래프 신경망은 여러 permutation equivariant / invariant 함수로 구성됩니다.

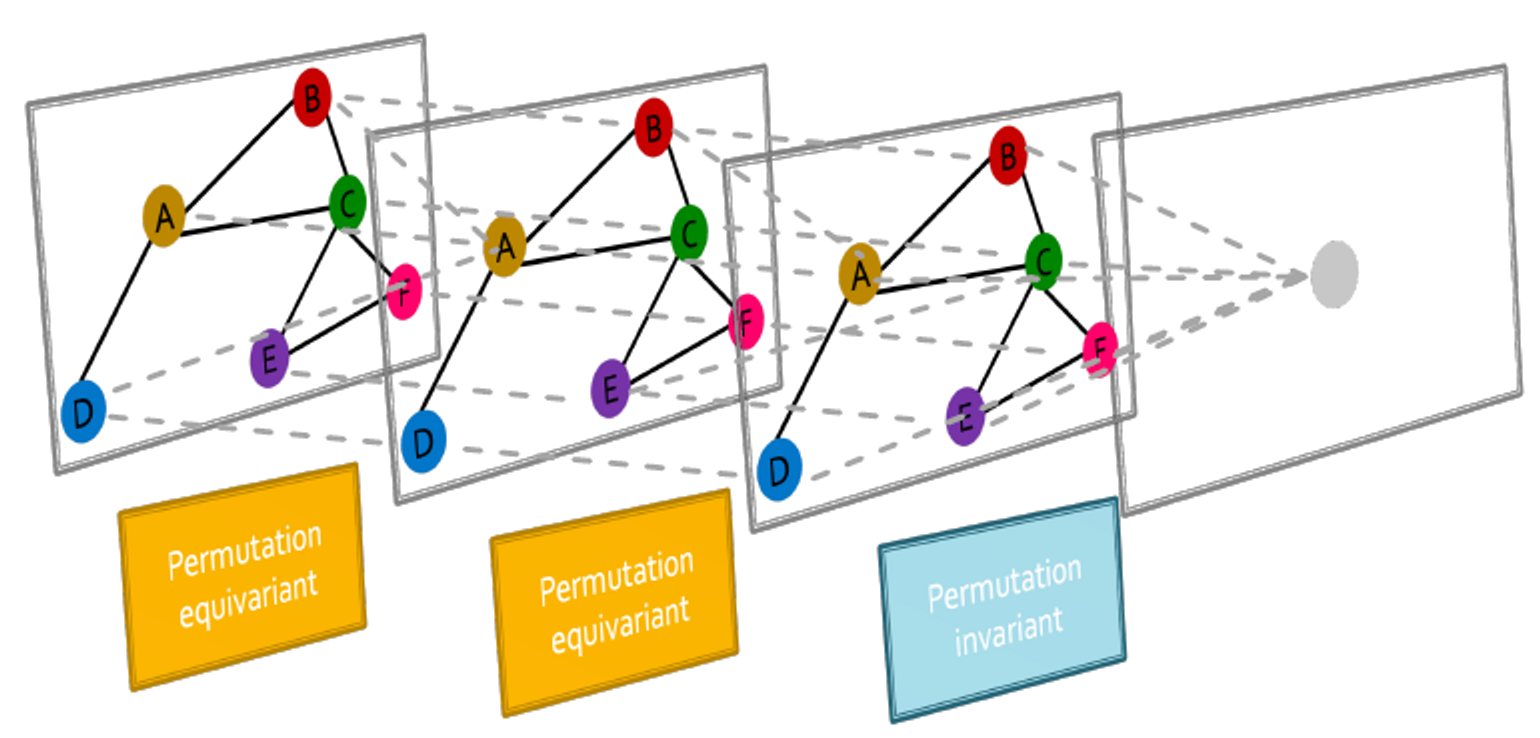
MLPs 같은 다른 신경망 아키텍처에도 permutation equivariant / invariant인지? 그렇지 않습니다. 입력값의 순서를 바꾸는 것은 다른 결과를 야기합니다.

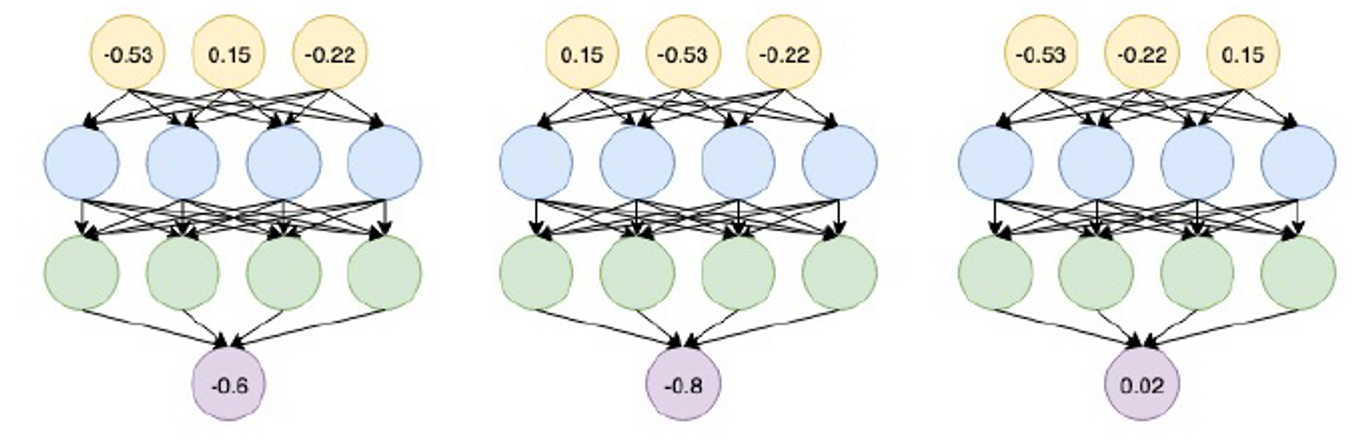
이 그림은 왜 MLP가 그래프로 표현되는 것이 실패되는지를 설명합니다.

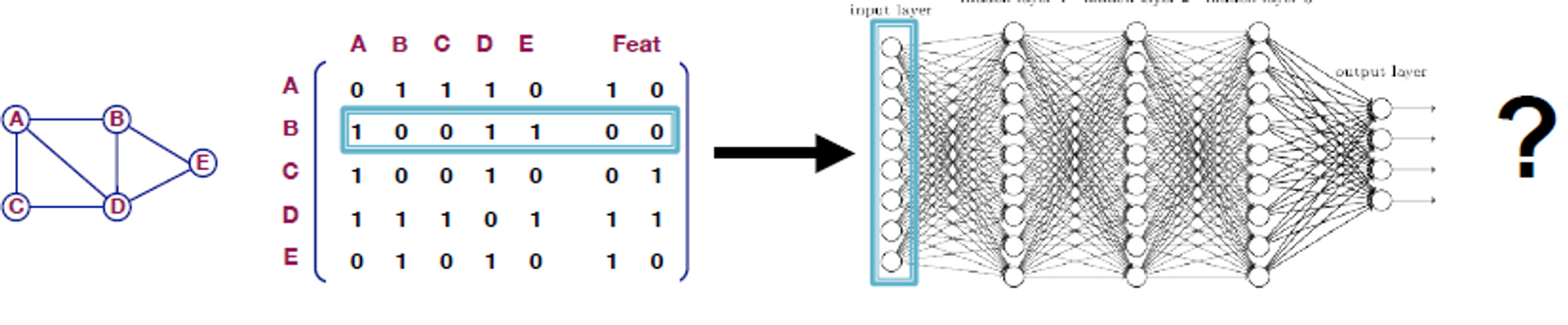
그래서 다음엔 이웃으로부터 정보를 전달하고 집계하는 (passing and aggregating) GNN을 설계합니다.

3. Graph Convolutional Networks

Graph Convolutional Networks

Idea:

노드의 이웃은 계산 그래프로 정의됩니다.

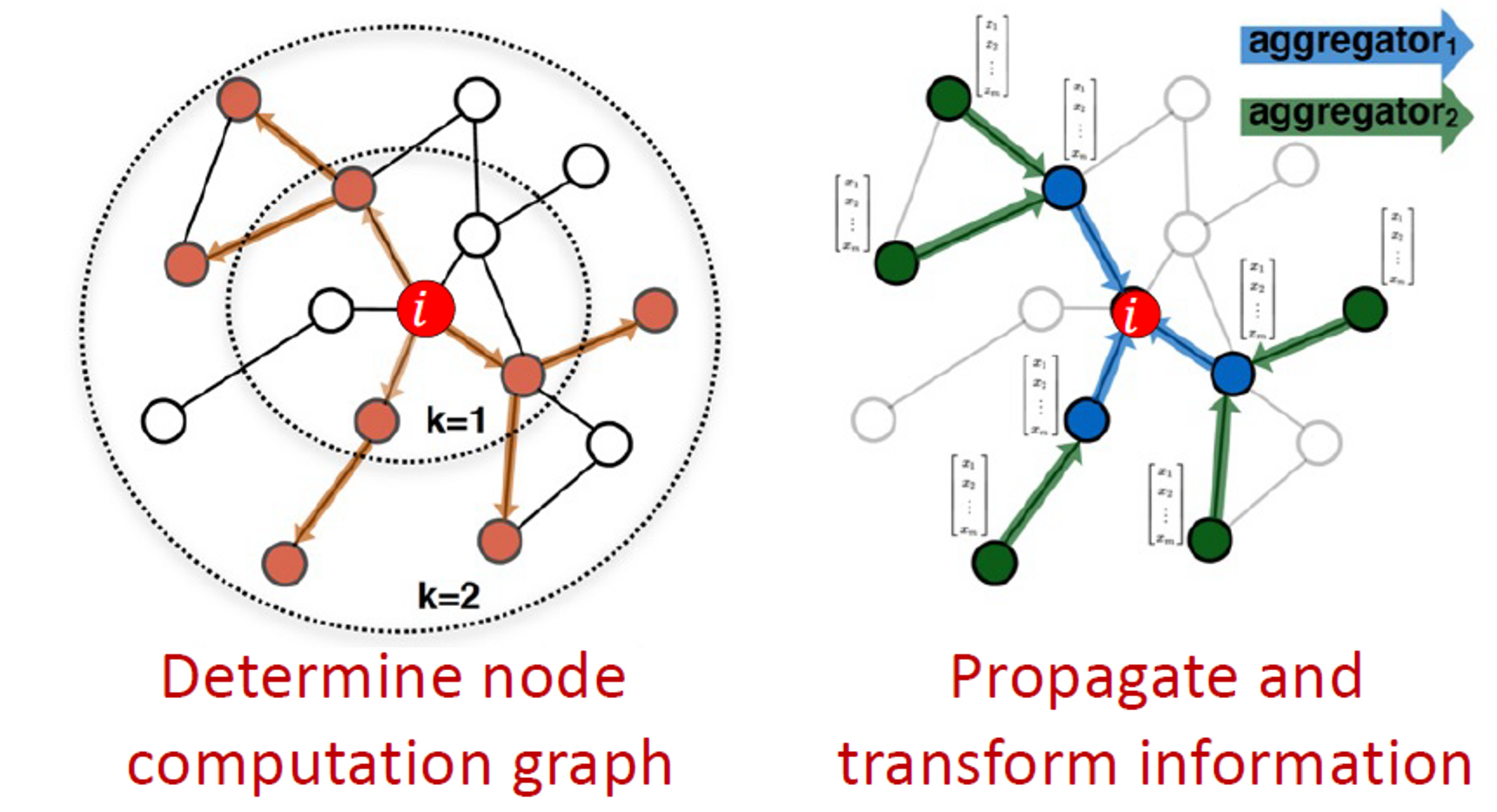
그래프에서 정보를 전파하여 노드 기능을 계산하는 방법을 학습합니다.

Idea: Aggregate Neighbors

Key Idea:

local network neighborhoods에 기반한 노드 임베딩을 생성합니다.

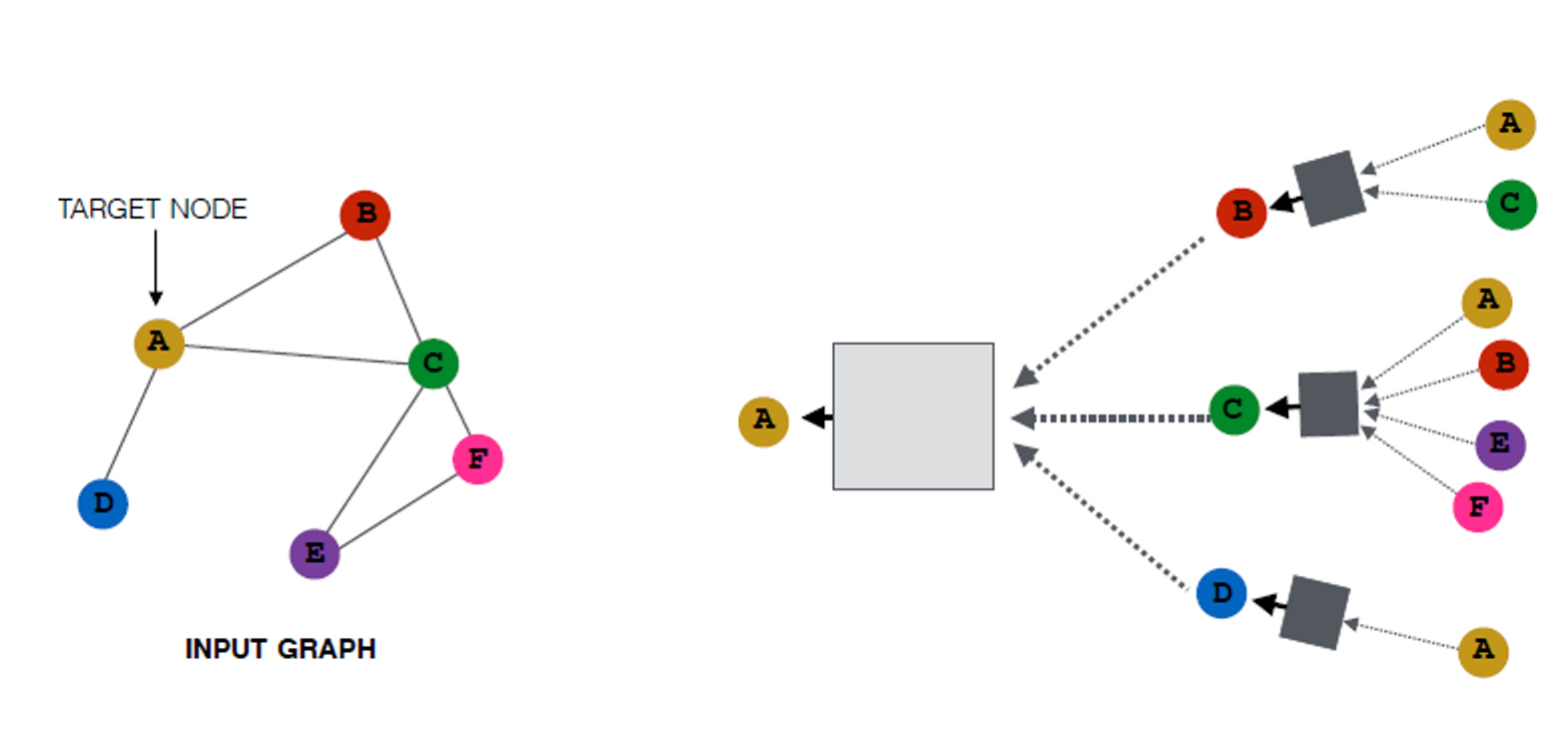
Intuition:

노드를 신경망을 사용해서 그들의 이웃으로부터 정보를 통합합니다.

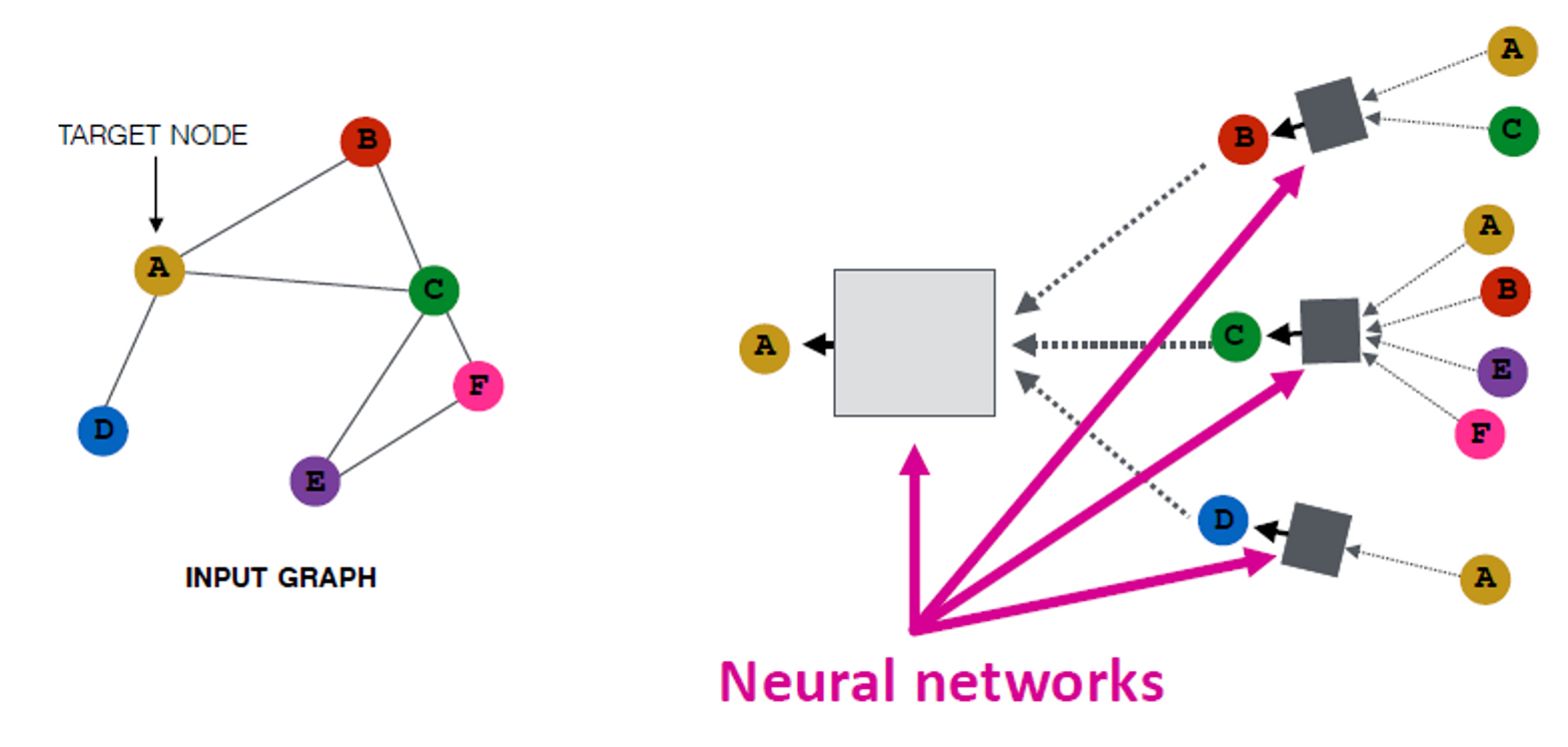
Intuition:

네트워크 이웃을 계산 그래프로 정의합니다.

모든 노드는 각 이웃에 기반하여 계산 그래프로 정의됩니다.

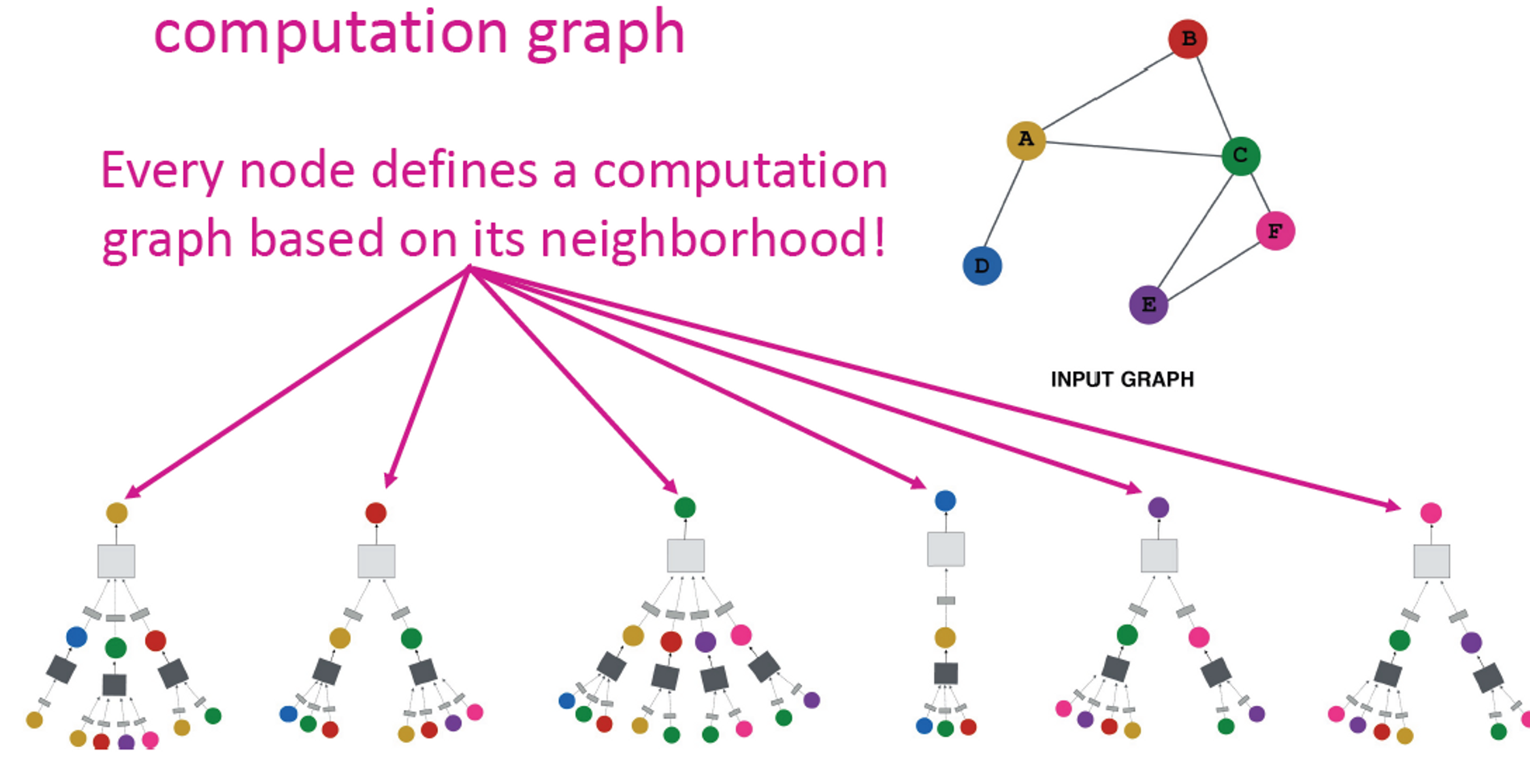
Neighborhood aggregation:

주요 차이점은 서로 다른 접근 방식이 계층 전체에서 정보를 집계하는 방법에 있습니다.

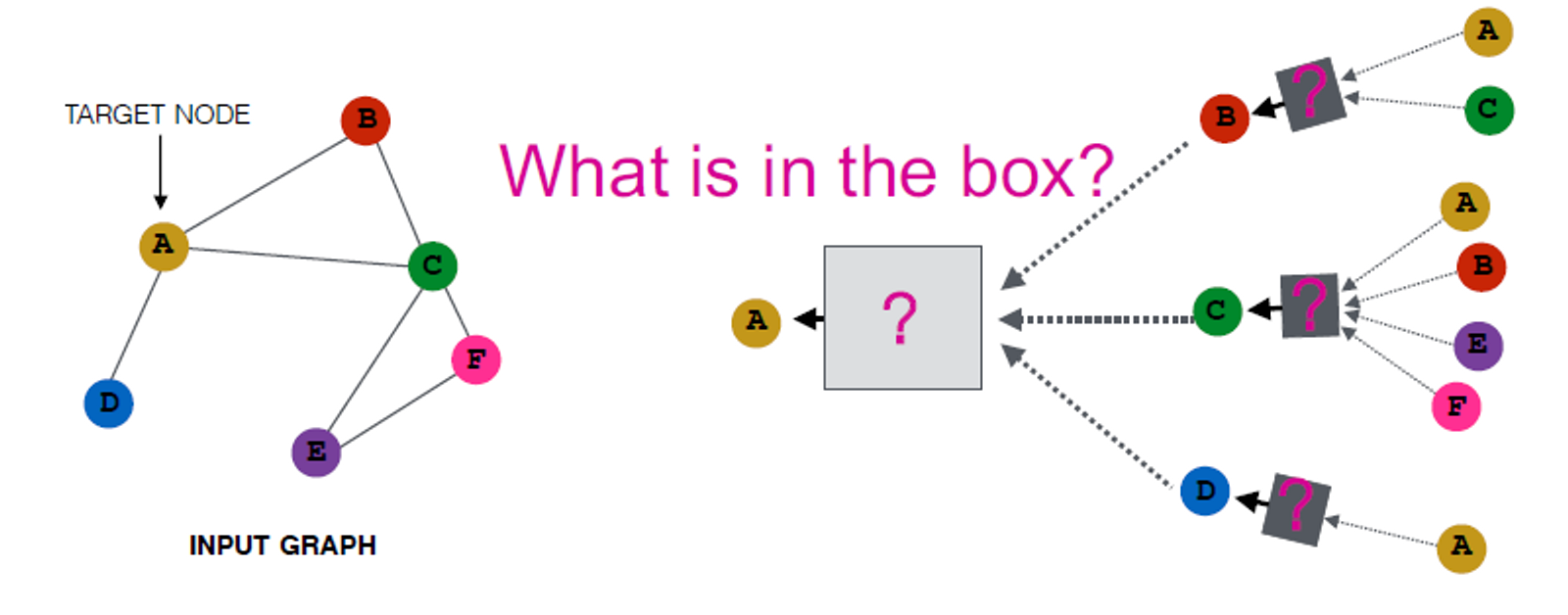
Basic approach:

이웃 정보 평균화 및 신경망 적용

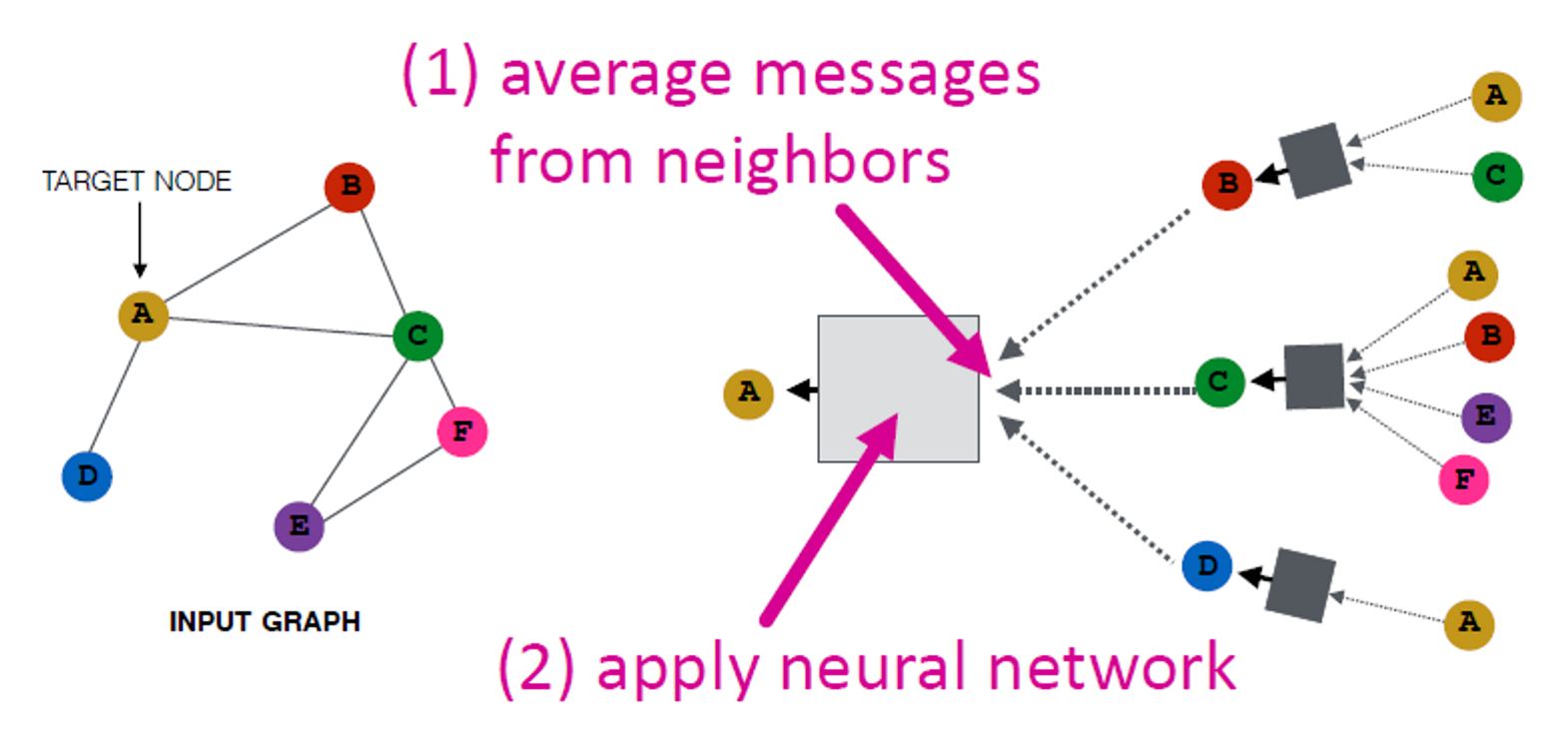
The Math: Deep Encoder

Basic approach:

이웃 메시지 평균화 및 신경망 적용

Equivariant Property

그래프 신경망에서 Message passing과 neighbor aggregation은 permutation equivariant입니다.

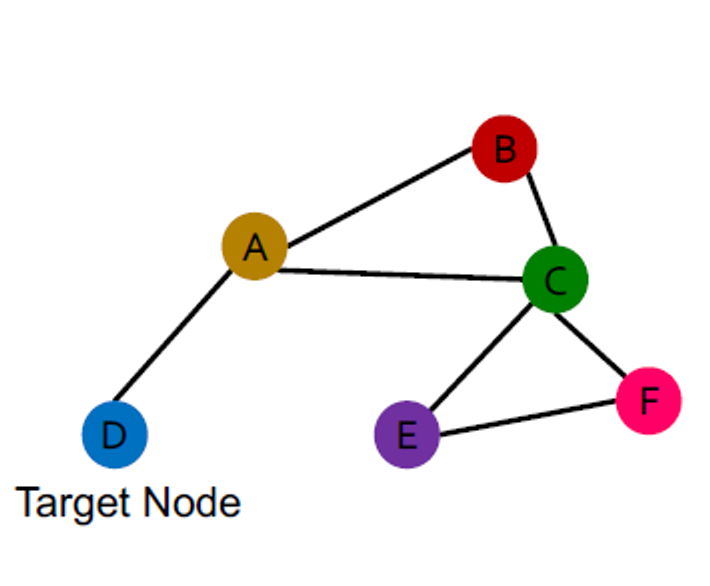
이런 그래프가 있을 때

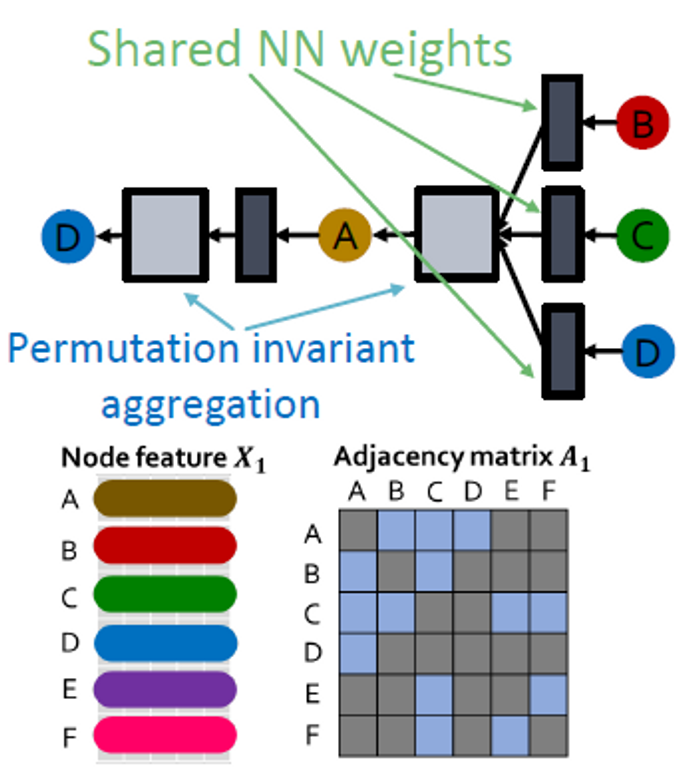
NN weights를 공유하고, permutation equivariant를 aggregation합니다.

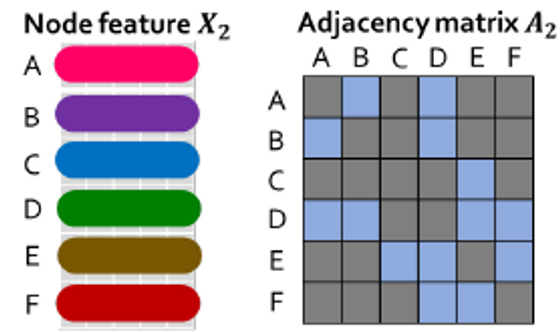
타겟 노드인 파란색은 다른 순서 계획에서도 같은 계산 그래프를 가집니다.

Training the Model

임베딩을 생성하도록 GCN을 어떻게 훈련하나요?

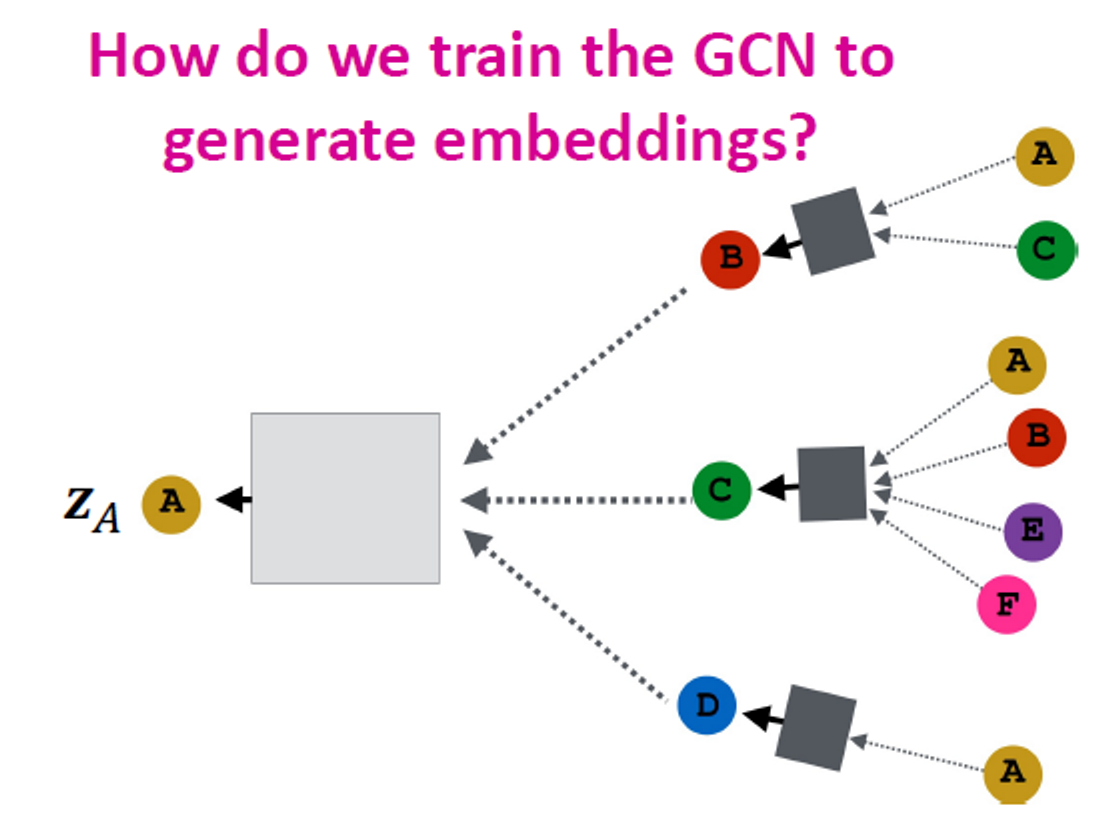
임베딩에서 손실 함수를 정의해야 합니다.

Model Parameters

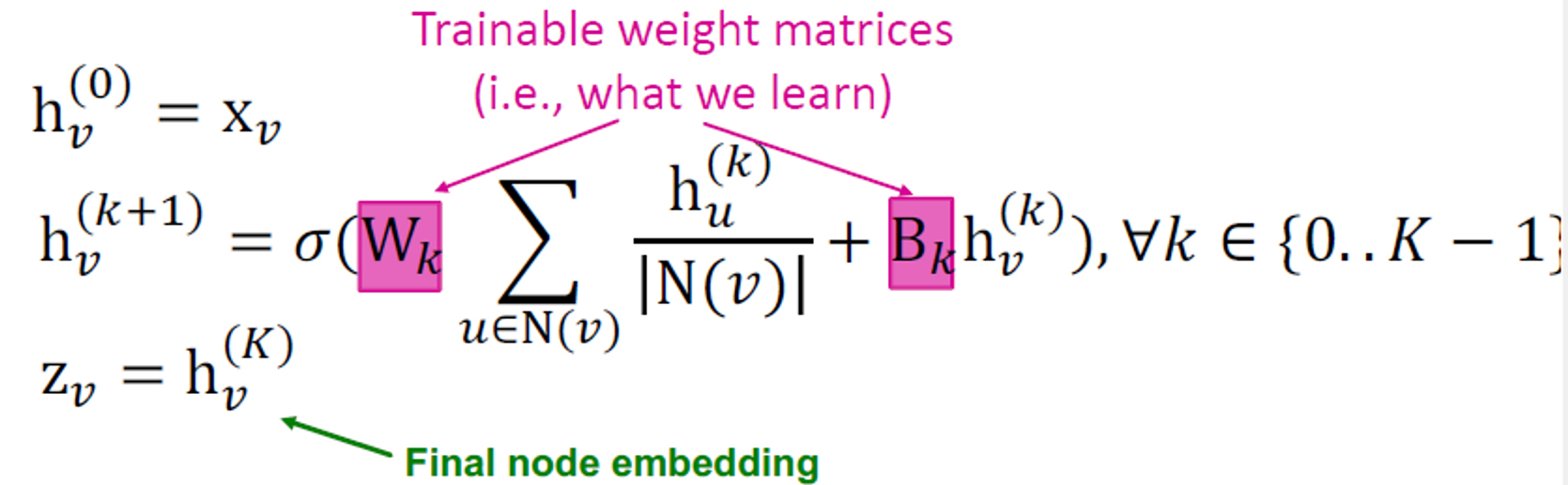
이러한 임베딩을 모든 손실 함수에 공급하고 SGD를 실행하여 가중치 매개변수를 훈련할 수 있습니다.

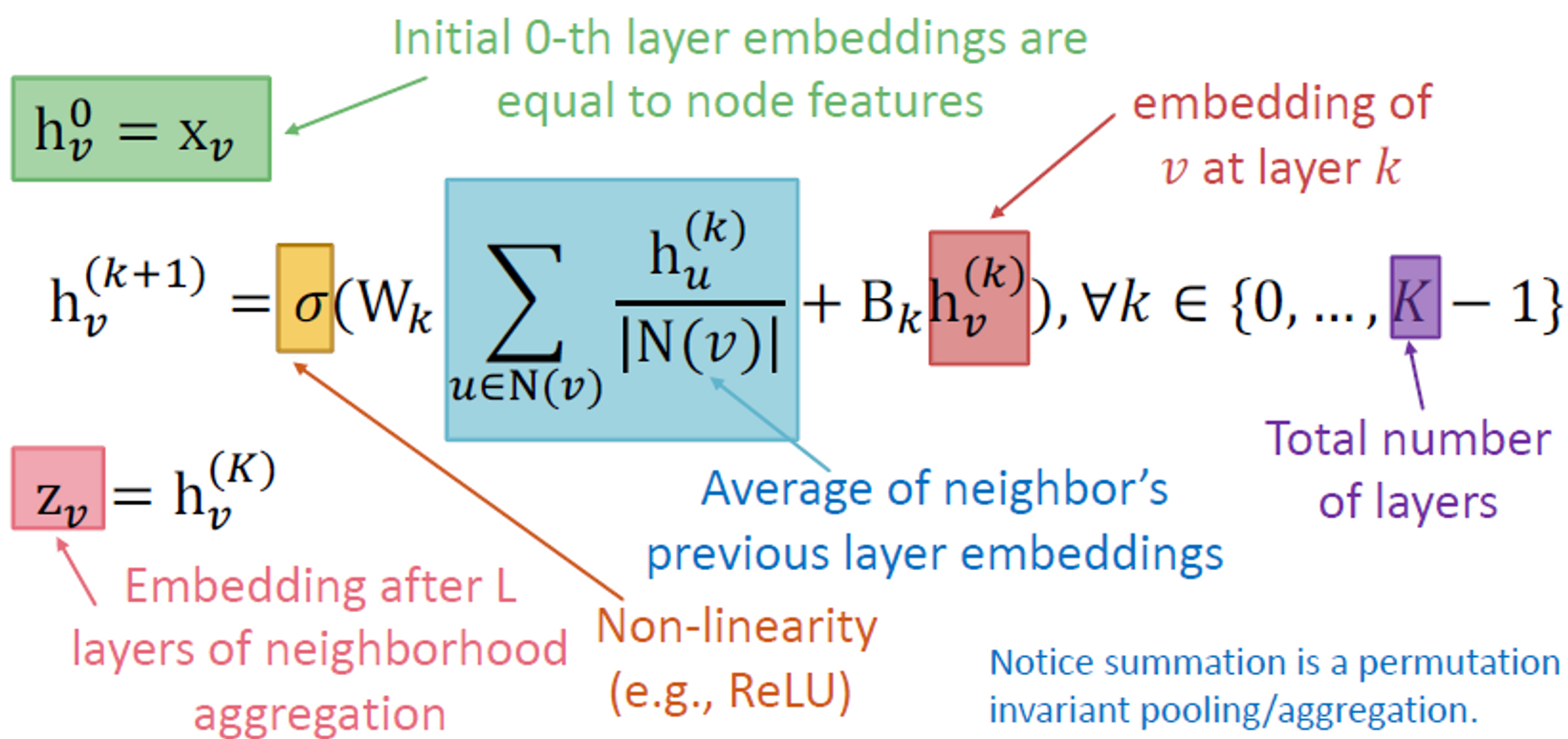
$h_v^k$: 레이어 $k$에서 노드 $v$의 hidden representation입니다.

• $W_k$: weight matrix for neighborhood aggregation
• $B_k$: weight matrix for transforming hidden vector of self

Matrix Formulation (1)

많은 aggregations은 행렬 연산으로 효율적으로 수행됩니다.

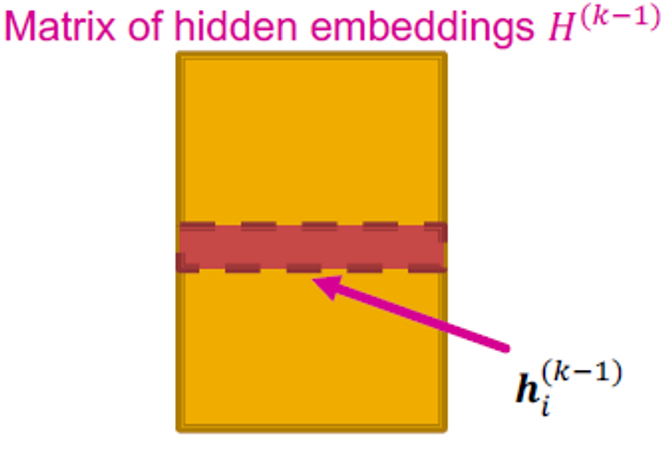
$H^{(k)} = [h_1^{(k)} \dots h_{|V|}^{(k)}]^T$이면, $\Sigma_{u\in N_v}h_u^{(k)} = A_{v,;}H^{(k)}$입니다.

대각 행렬 D는 $D_{v,v} = Deg(v) = |N(v)|$이고, $D$의 역행렬 $D^{-1}$은 대각 원소입니다. → $D_{v,v}^{-1} = 1/|N(v)|$그

그러므로

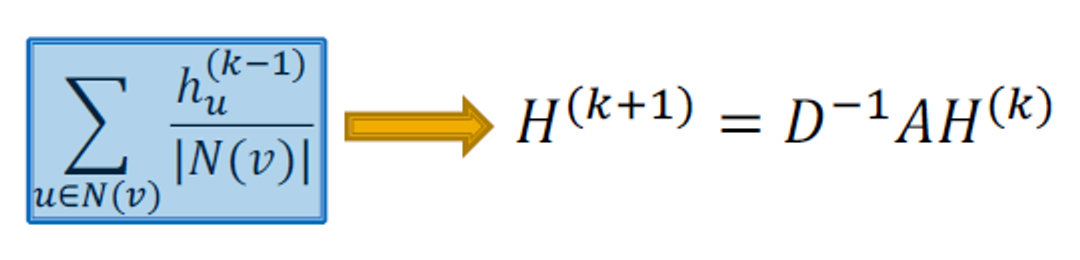
Matrix Formulation (2)

업데이트된 함수를 행렬 형태로 다시 적는다면

$H^{(k+1)} = \sigma(\tilde{A}H^{(k)}W_k^T + H^{(k)}B_k^T)$ where $\tilde{A} = D^{-1}A$

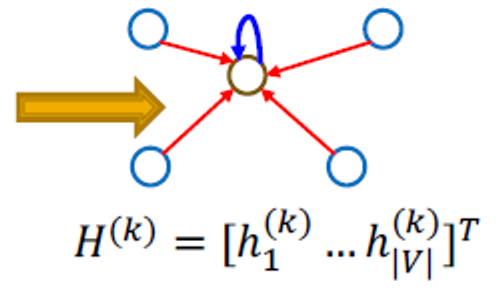
• Red: neighborhood aggregation
• Blue: self transformation

실제로 이는 효율적인 희소 행렬 곱셈을 사용할 수 있음을 의미합니다($\tilde{A}$은 희소함).

• 참고: 집계 함수가 복잡한 경우 모든 GNN을 행렬 형식으로 표현할 수 있는 것은 아닙니다.

How to Train A GNN

• 노드 임베딩 $𝒛_v$은 입력 그래프의 함수입니다.
• Supervised setting: 손실 $L$을 최소화하고 싶습니다. → $min_{\theta} L(y, f(x))$
• $𝒚$: node label
• $L$ could be $L2$ if $𝒚$ is real number, or cross entropy if $𝒚$ is categorical
• Unsupervised setting: 사용 가능한 노드 레이블 없습니다. 그래프 구조를 supervised로 사용해야 합니다.

Unsupervised Training

“Similar” nodes have similar embeddings

$L = \Sigma_{z_u, z_v} CE(y_{u,v}, DEC(z_u, z_v))$

• 노드 $u, v$가 비슷하면 $y_{u,v}=1$입니다.
• CE는 크로스 엔트로피입니다.
• DEC는 내적과 같은 디코더입니다.
• 노드 유사도는 어떤 것이든 될 수 있습니다. (lecture 3 참고)
  • Random walks (node2vec, DeepWalk, struc2vec)
  • Matrix factorization
  • Node proximity in the graph

Supervised Training

지도 작업을 위해 모델을 직접 훈련합니다. (예: 노드 분류)

크로스 엔트로피를 사용합니다.

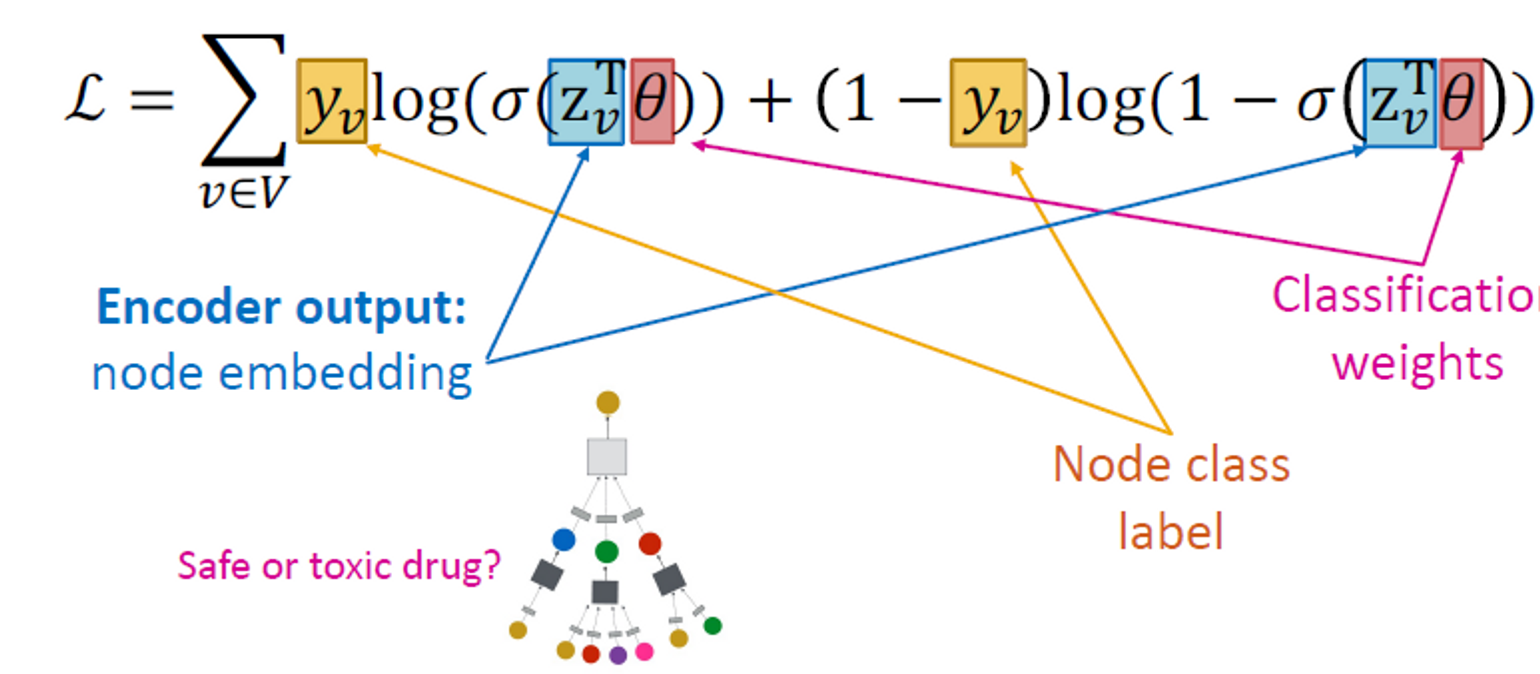
Model Design: Overview

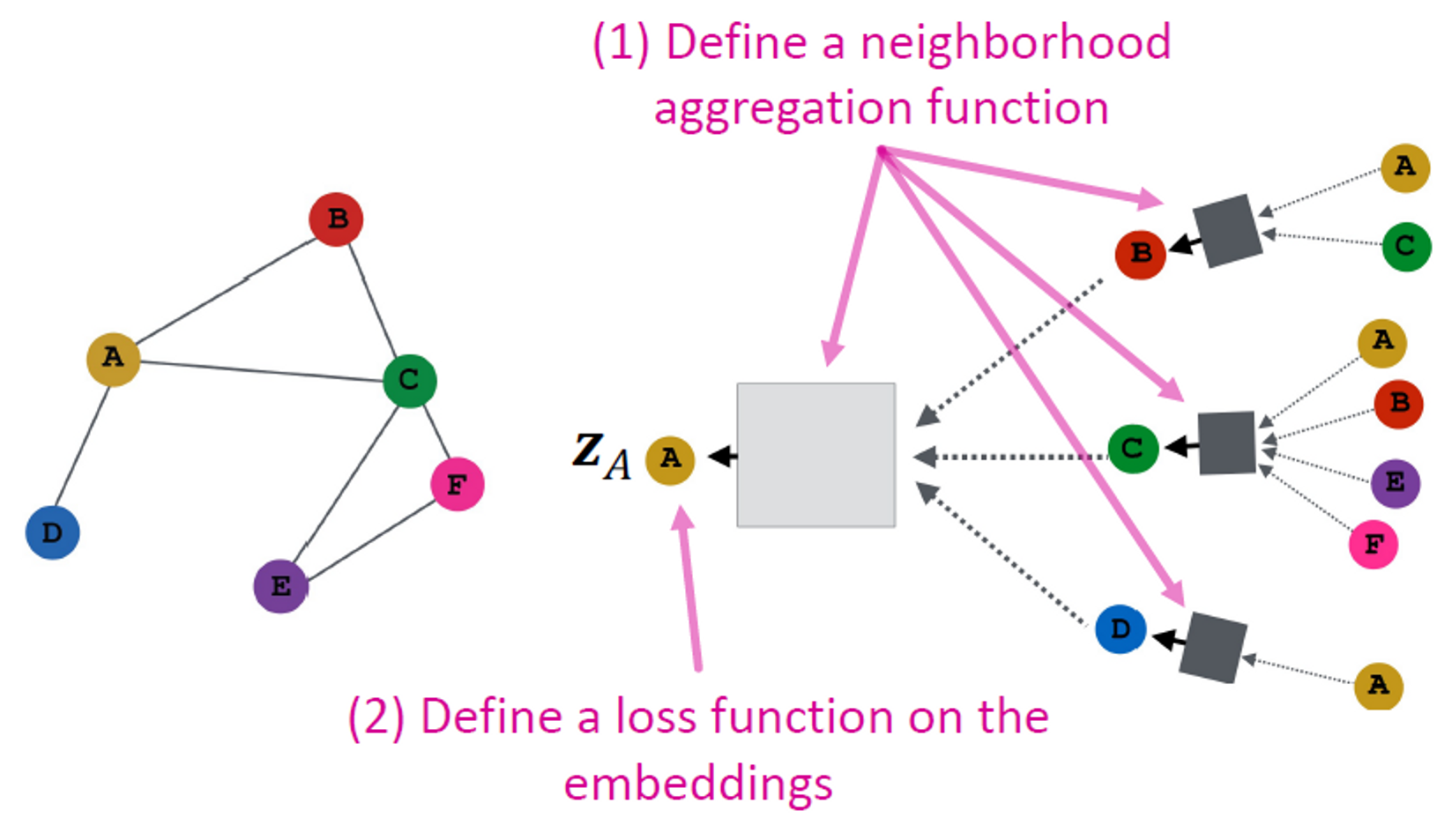
(1) Define a neighborhood aggregation function

(2) Define a loss function on the embeddings

(3) Train on a set of nodes, i.e., a batch of compute graphs

(4) Generate embeddings for nodes as needed

→ Even for nodes we never trained on!

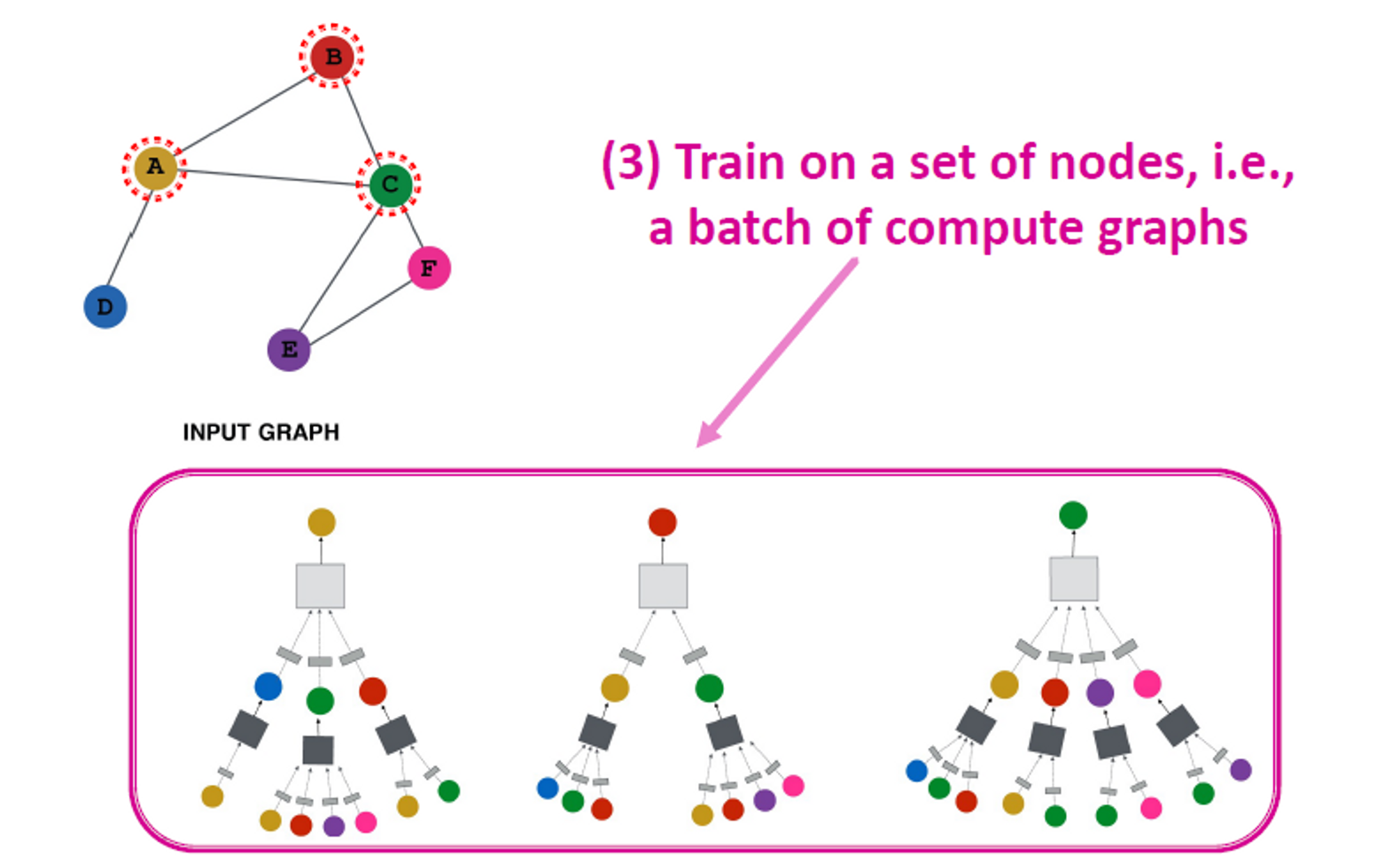
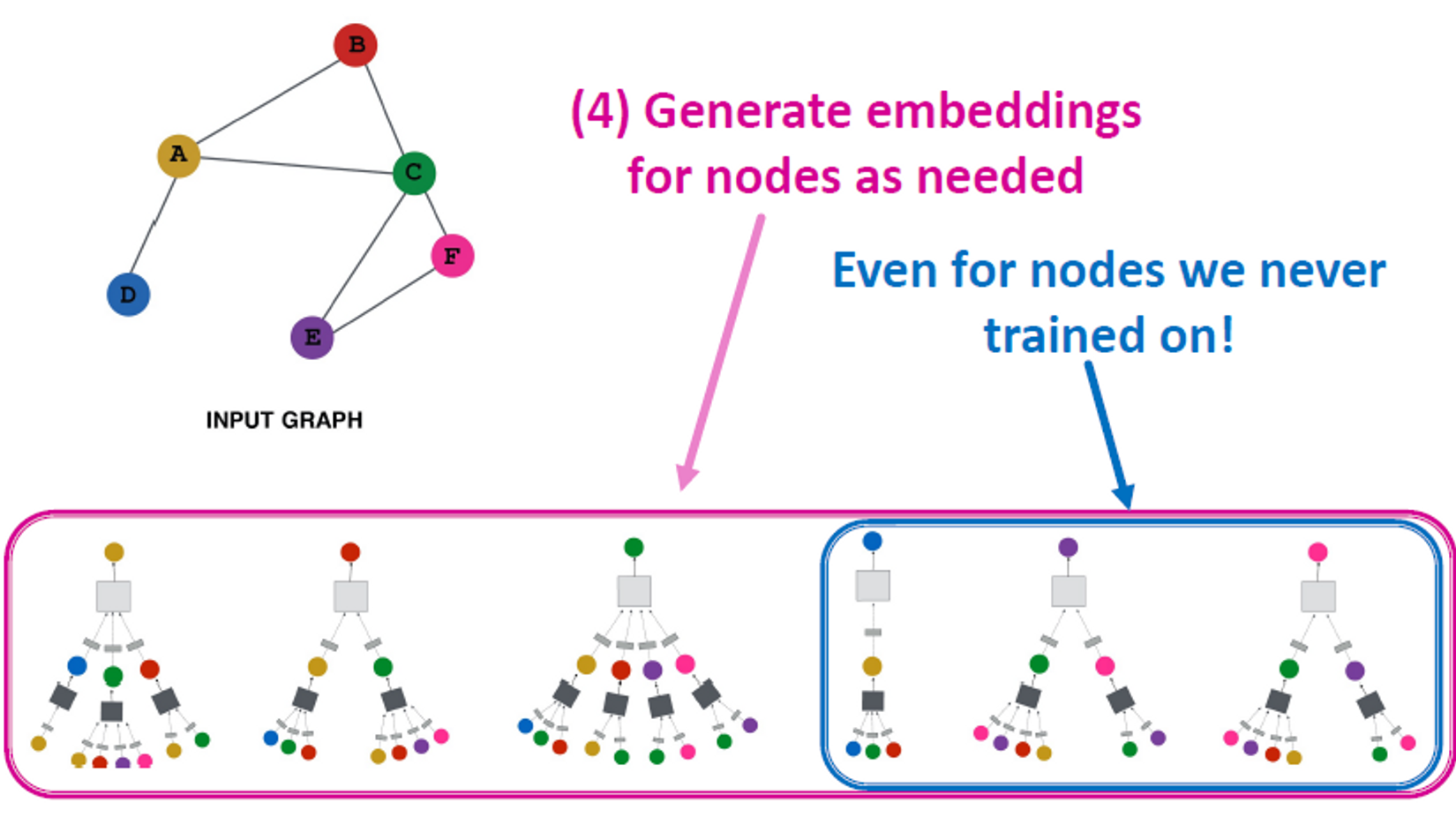
Inductive Capability

동일한 집계 매개변수가 모든 노드에 대해 공유됩니다. 모델 매개변수의 수는 |𝑉|에서 sublinear이고, 보이지 않는 노드로 일반화할 수 있습니다.

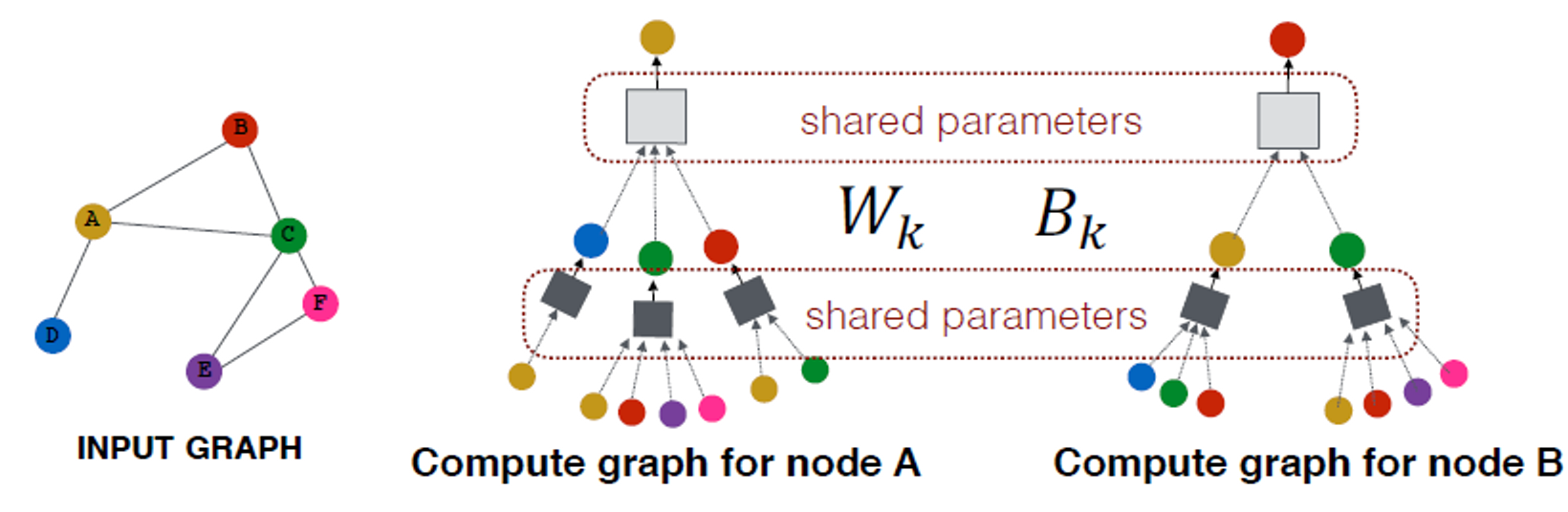
Inductive Capability: New Graphs

예를 들어, 모델 유기체 A의 단백질 상호 작용 그래프에 대해 학습하고 유기체 B에 대해 새로 수집된 데이터에 임베딩을 생성합니다.

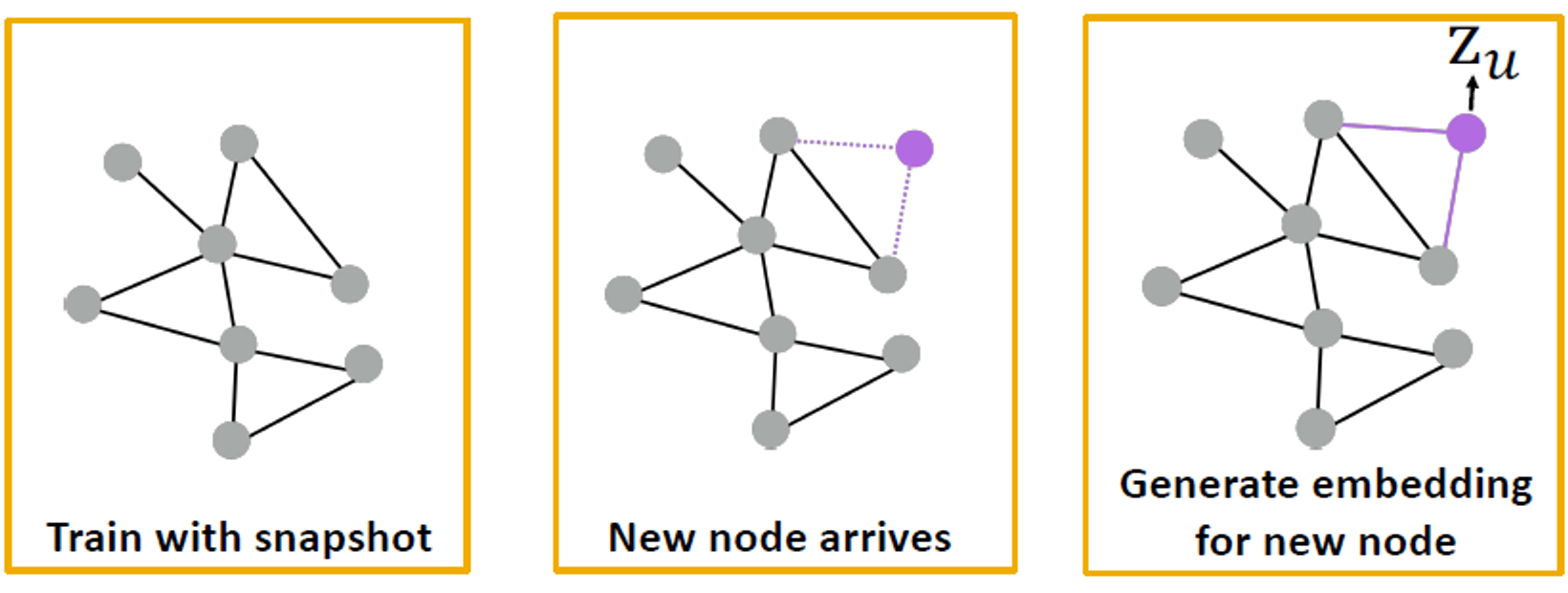
Inductive Capability: New Nodes

• 많은 애플리케이션 설정에서 이전에 볼 수 없었던 노드가 지속적으로 발생합니다.
• 예: Reddit, YouTube, Google Scholar
• 새로운 임베딩을 "즉석에서" 생성해야 함

4. GNNs subsume CNNs and Transformers

Architecture Comparison

GNN은 Convolutional Neural Nets 및 Transformers와 같은 주요 아키텍처와 어떻게 비교됩니까?

Convolutional Neural Network

3x3 필터가 있는 컨벌루션 신경망(CNN) 레이어:

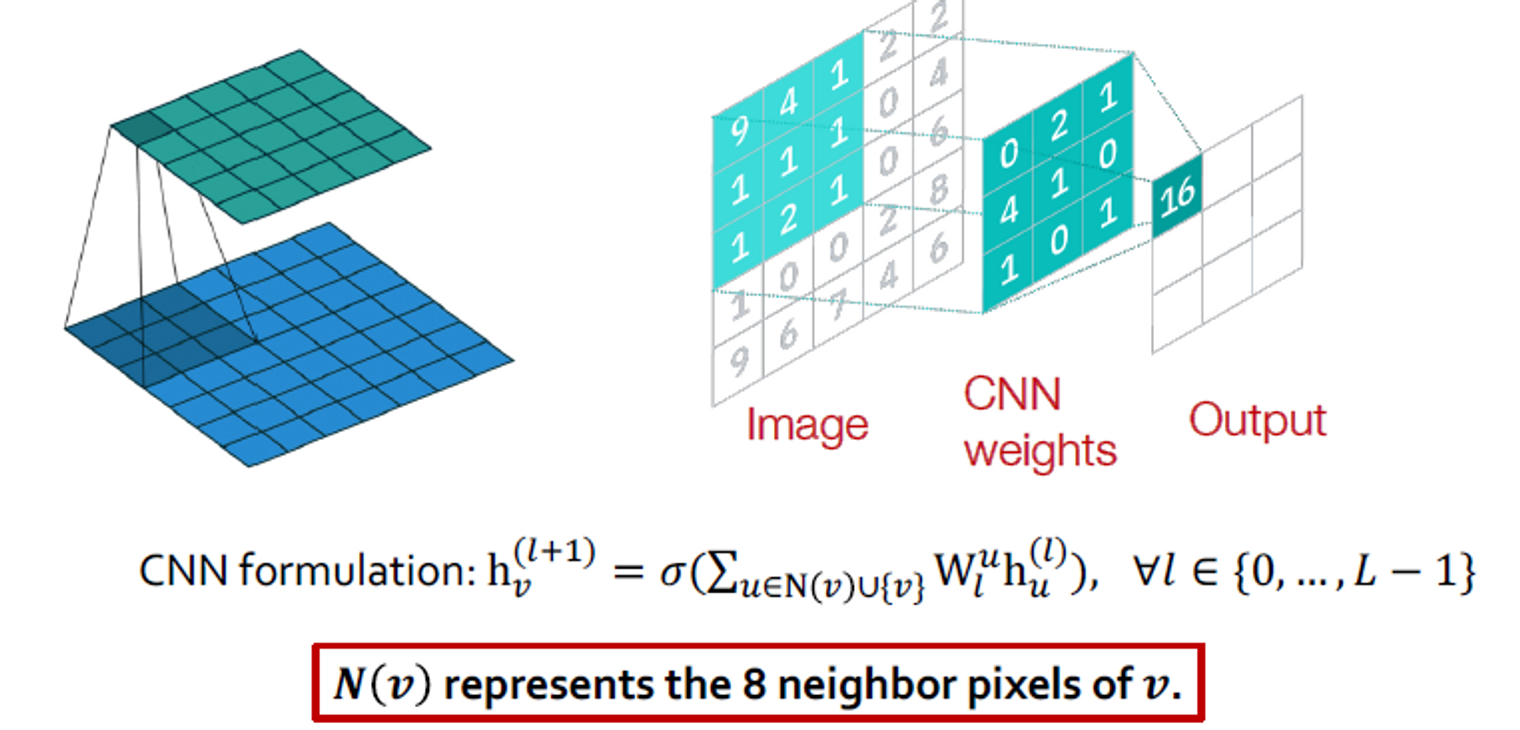
GNN vs. CNN

3x3 필터가 있는 컨벌루션 신경망(CNN) 레이어:

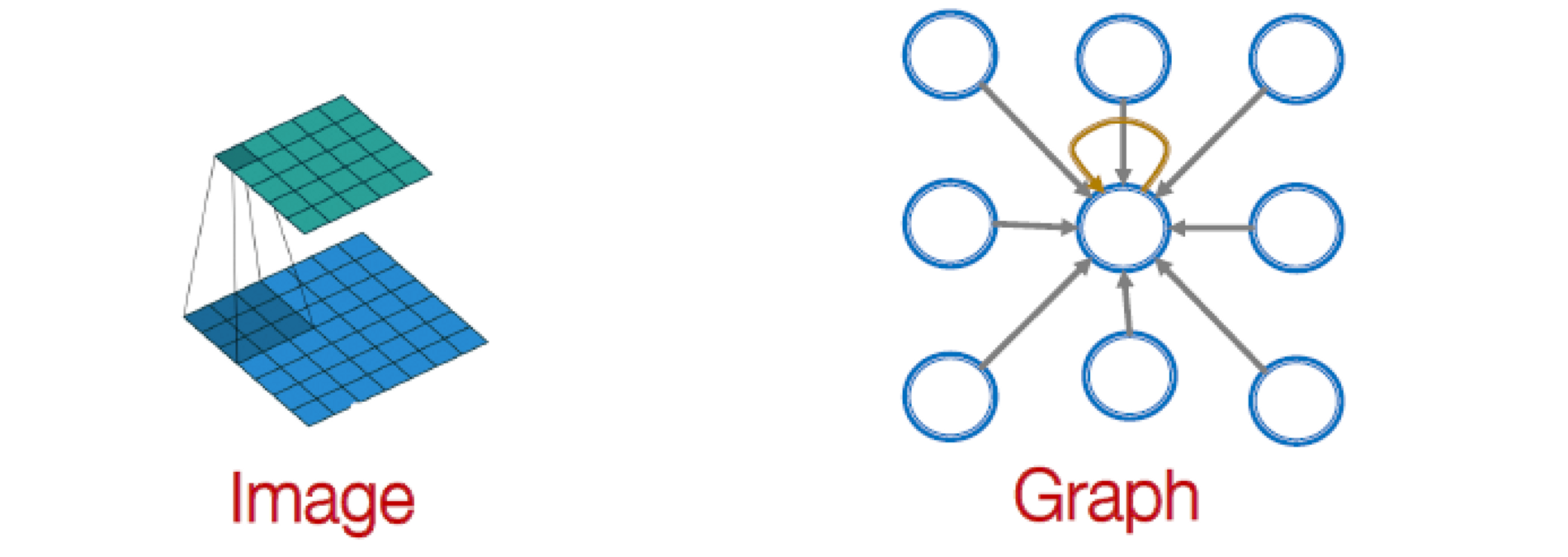
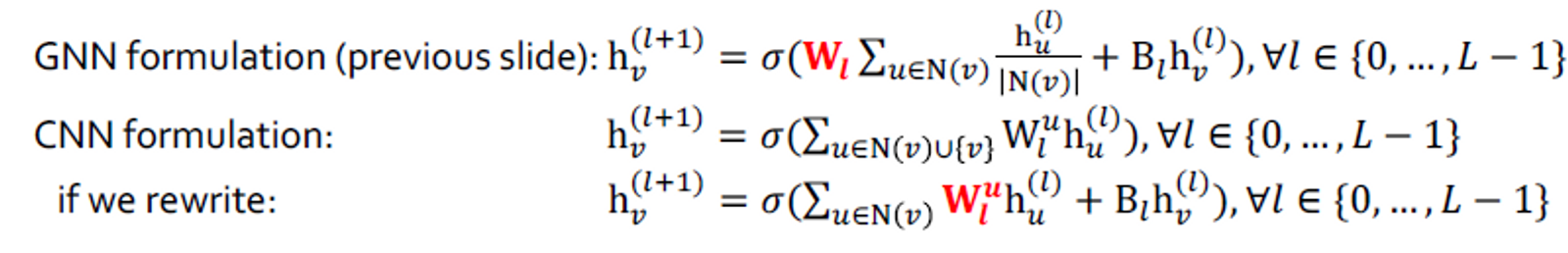
주요 차이점: 이미지의 픽셀 $𝑣$에 대해 서로 다른 "이웃" $𝑢$에 대해 서로 다른 $𝑊$를 학습할 수 있습니다. 그 이유는 중앙 픽셀에 대한 상대 위치 {(-1,-1), (-1,0), (-1, 1), …, (1, 1)}을 사용하여 9개의 이웃에 대한 순서를 선택할 수 있기 때문입니다.

CNN은 이웃 크기와 순서가 고정된 특별한 GNN으로 볼 수 있습니다.

• 필터의 크기는 CNN에 대해 미리 정의됩니다.
• GNN의 장점은 각 노드에 대해 다른 차수로 임의의 그래프를 처리한다는 것입니다.
• CNN은 permutation equivariant이 아닙니다.
• 픽셀 순서를 전환하면 다른 출력이 생성됩니다.

Transformer

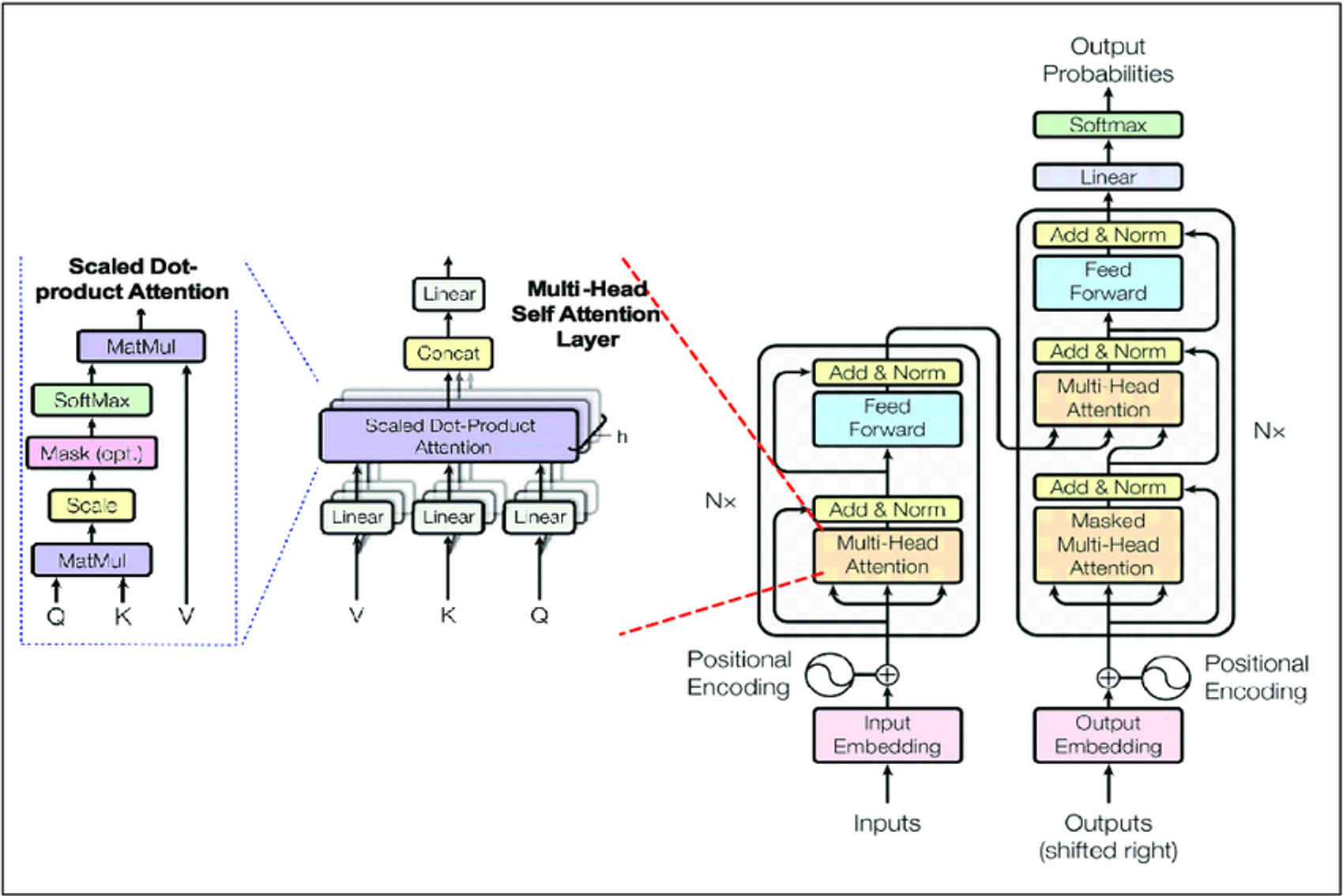
트랜스포머는 많은 시퀀스 모델 작업에 있어서 좋은 성능을 달성한 가장 인기 있는 아키텍처 중 하나입니다.

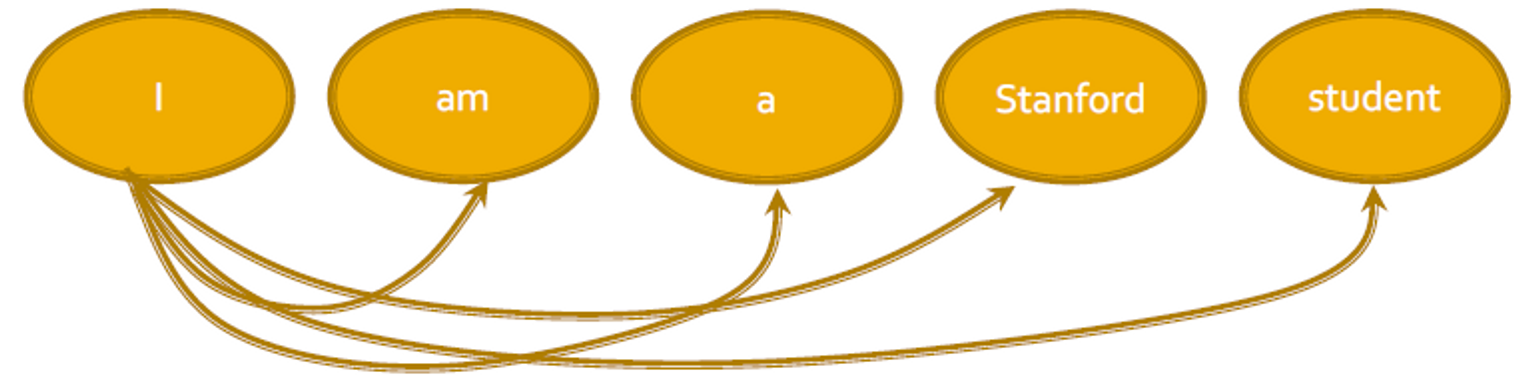
Key component: self-attention

• 모든 토큰과 단어는 행렬 계산에 의해 다른 토큰과 단어로 관심을 집중(attention)합니다.

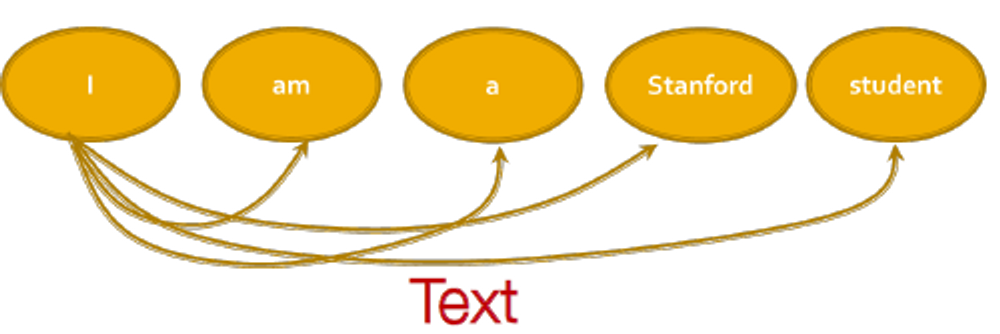
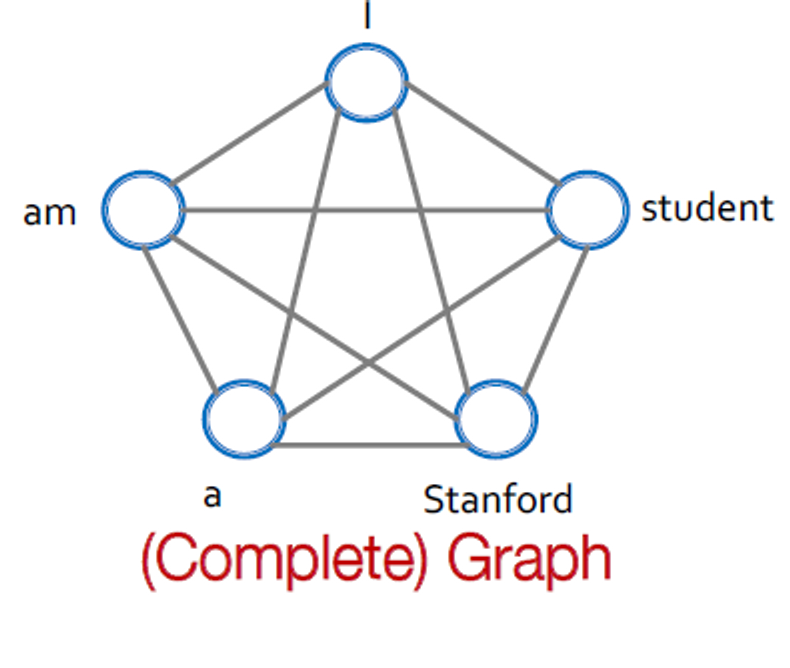
GNN vs. Transformer

트랜스포머 레이어는 ‘word’ 그래프로 fully-connected되는 특별한 GNN으로 보입니다. 각 단어가 다른 모든 단어에 참여하기 때문에 변환기 계층의 계산 그래프는 완전히 연결된 "단어" 그래프에서 GNN의 계산 그래프와 동일합니다.

Summary

이번 강의에서 소개해드린 것은

• 신경망의 기초
  • 손실, 최적화, 기울기, SGD, 비선형성, MLP
• 그래프를 위한 딥러닝 아이디어
  • 임베딩 변환의 여러 계층
  • 모든 레이어에서 이전 레이어의 임베딩을 입력과 같이 사용합니다.
  • 이웃 및 자체 임베딩의 집계
• 그래프 컨벌루션 네트워크
  • Mean aggregation;; 행렬 형식으로 표현할 수 있습니다.
• GNN은 일반 아키텍처입니다.
  • CNN과 Transformer는 특별한 GNN으로 볼 수 있습니다.