Convex Hull 알고리즘

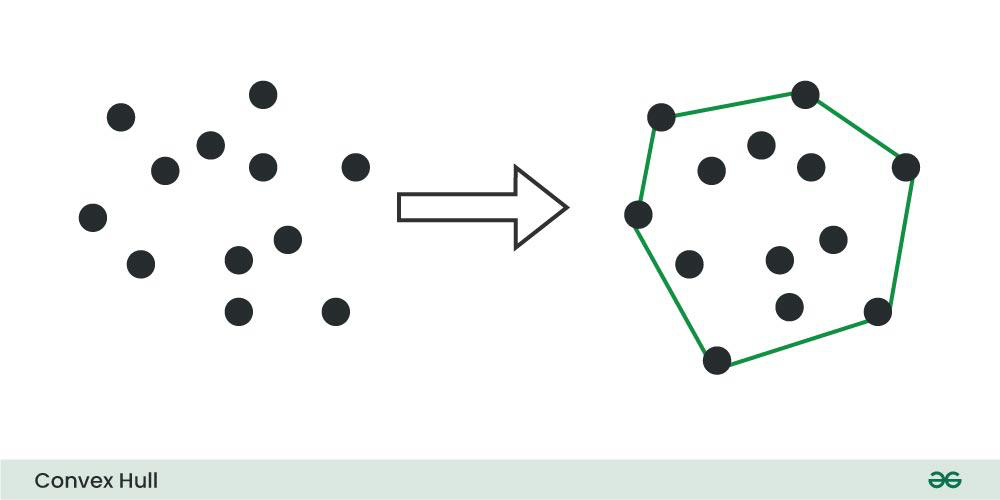
사진 출처: Convex Hull Algorithm

Convex Hull (컨벡스 헐)

개념

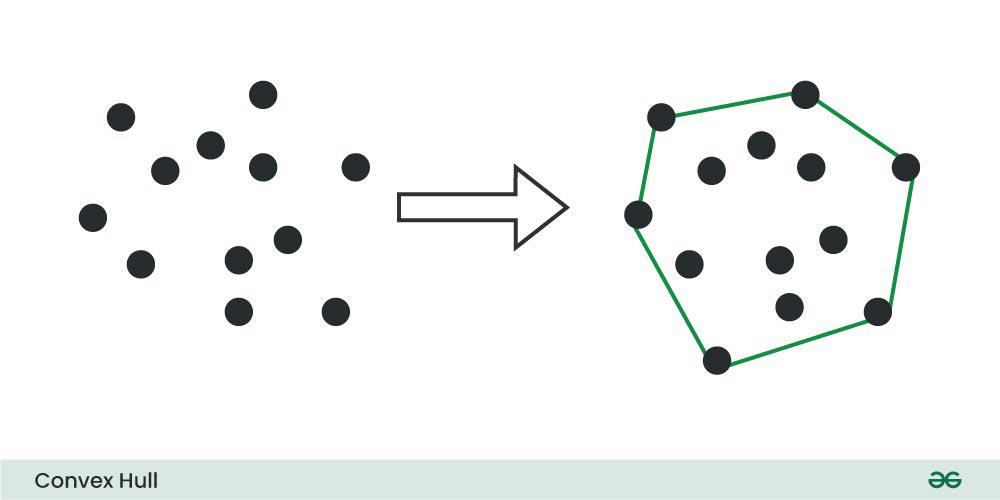
Convex Hull은 2차원 좌표 평면에 존재하는 점들의 집합을 감싸는 최소 크기의 볼록 다각형(Convex Polygon)을 말한다.

특징

1. Convex Hull은 점들을 포함하는 영역(내부)과 포함하지 않는 영역(외부)을 나누는 경계 역할을 한다.
2. Convex Hull 내부에는 모든 점들이 포함되며, 외부 영역에는 점들이 존재하지 않는다,
3. 여러 점 중 일부 점들을 이용해 구성되며, 면적이 최소인 볼록 다각형을 형성한다.

Convex Hull의 필요성

• 2차원 좌표 평면에서 모든 점을 다루는 것은 비효율적입니다. 관심 있는 구간(영역)을 좁히기 위해 Convex Hull을 사용한다.
• 이를 통해 탐색 범위를 줄이고, 필요한 점만 추출할 수 있다.

Convex Hull의 시각적 이해

1. 2차원 좌표 평면에 여러 점이 주어진다.
2. 이 점들을 모두 포함하는 볼록 다각형을 그린다.
   • 볼록 다각형의 각 변은 점과 점을 연결하여 형성됩니다.
3. Convex Hull은 외곽 점들만 연결하며, 이 외곽 점들이 Convex Hull의 경계선을 형성한다.

Convex Hull을 구하는 알고리즘

주요 알고리즘

• Convex Hull을 구성하는 점들을 구하는 알고리즘은 여러 가지가 있습니다. 대표적인 방법으로:
  1. Graham Scan
     • 시간 복잡도:
       • 점 정렬 등 전처리: O(NlogN)
       • Convex Hull 계산: O(N)
  2. Jarvis March (Gift Wrapping)

Graham Scan 알고리즘

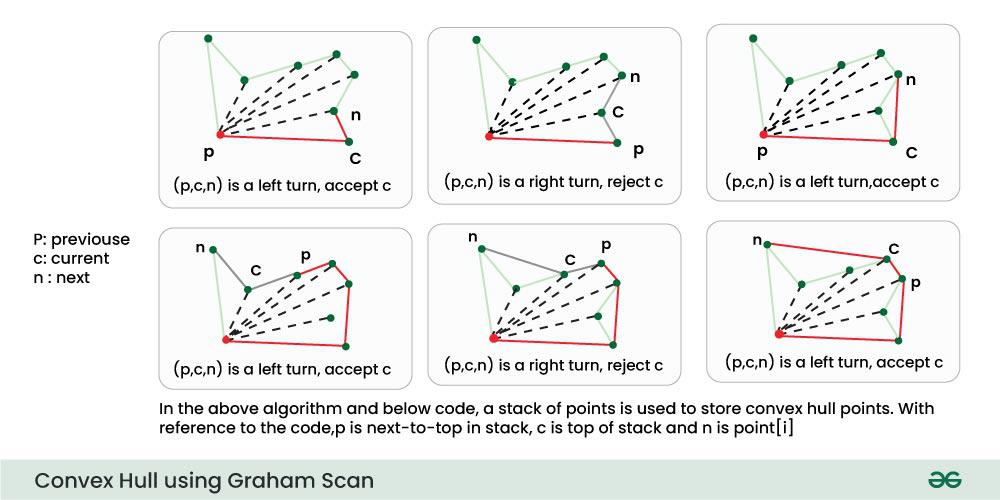
• 주어진 점들의 좌표를 기반으로 볼록 껍질을 구성하는 점들을 효율적으로 계산하는 알고리즘.
• 단계:
  1. 기준점 선택: 가장 아래쪽(y가 최소) 또는 왼쪽(x가 최소)인 점 선택.
  2. 각도 기준 정렬: 기준점에서 다른 점들과 이루는 각도에 따라 점들을 정렬.
  3. Convex Hull 형성:
     • 정렬된 점을 따라가며 볼록 껍질을 형성.
     • 현재 점이 볼록 다각형의 일부인지 아닌지 확인.