요즘은 공부 벌레🐛가 되고 싶은... 부족한 딥러닝 지식을 채우기 위해 고군분투 중...🥺
참고 자료
📚 딥러닝 교과서, 출판사: 이지스 퍼블리싱
🔗 [Python] 성능 측정 지표 :: MAE, MSE, RMSE, MAPE, MPE, MSLE
🔗 공돌이의 수학정리노트
목차
- 손실 함수 정의 기준
1) 오차 최소화(error minimization)
2) 최대우도추정(maximum likelihood estimation) - 오차 최소화 관점에서 손실 함수 정의
1) 평균제곱오차(MSE)
2) 평균절대오차(MAE)
3) MSE vs MAE - MLE란?
1) Likelihood function의 최대값을 찾는 방법
2) 최대화 문제를 최소화 문제로 변환하는 방법 - MLE 손실함수 정의
1) 회귀 문제
2) 이진 분류 문제
3) 다중 분류 문제 - 신경망 학습을 위한 손실 함수
- 추천 자료
챕터 3에서는 회귀 모델과 분류 모델을 학습하기 위한 최적화 문제를 정의했습니다.
이번에는 최적화 문제의 손실 함수는 어떤 기준으로 정의해야 하며 어떤 의미로 해석해야 하는지를 정리하는 글입니다.
- 수학 수식 기반 과정 유도를 정리할 예정입니다.
- 제약 조건이 있는 최적화 문제를 처리하는 최적화 알고리즘을 적용합니다.
1. 손실 함수 정의 기준
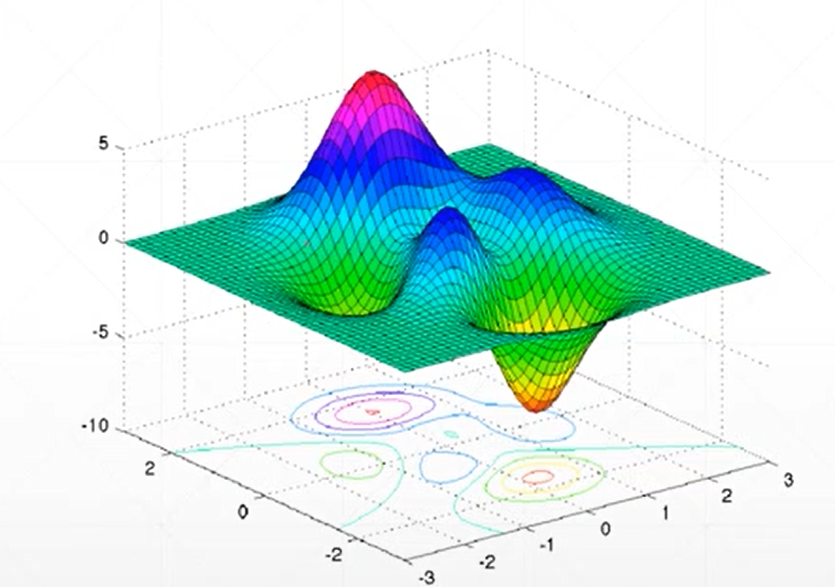
신경망 모델이 정확하게 예측하려면 모델은 관측 데이터를 잘 설명하는 함수를 표현해야 합니다.
이때 모델이 표현하는 함수의 형태를 결정하는 것이 바로 손실 함수입니다.
따라서 손실 함수는 모델이 관측 데이터를 잘 표현하도록 정의되어야 합니다!
손실함수가 위 그림과 같을 때, 가장 아래로 볼록하게 내려간 부분의 파라미터값이 손실 함수의 최적해가 됩니다.
모델은 손실 함수의 최적해로 파라미터화 된 함수를 표현합니다.
손실 함수가 달라지면 최적해도 바뀌므로 관측 데이터를 잘 설명하는 함수를 표현하려면, 손실함수는
최적해가 관측 데이터를 잘 설명할 수 있는 함수의 파라미터 값이 되도록
정의되어야 합니다.
그러면 그렇게 정의되기 위해 정의하는 기준은 두 가지 관점이 있습니다.
- 오차 최소화(error minimization)
- 최대우도추정(maximum likelihood estimation)
오차 최소화는 모델이 오차가 최소화 되도록 정의하는 방법입니다.
최대 우도 추정은 모델이 추정하는 관측 데이터의 확률이 최대화 되도록 정의하는 방법이 있습니다.
1) 오차 최소화(error minimization)
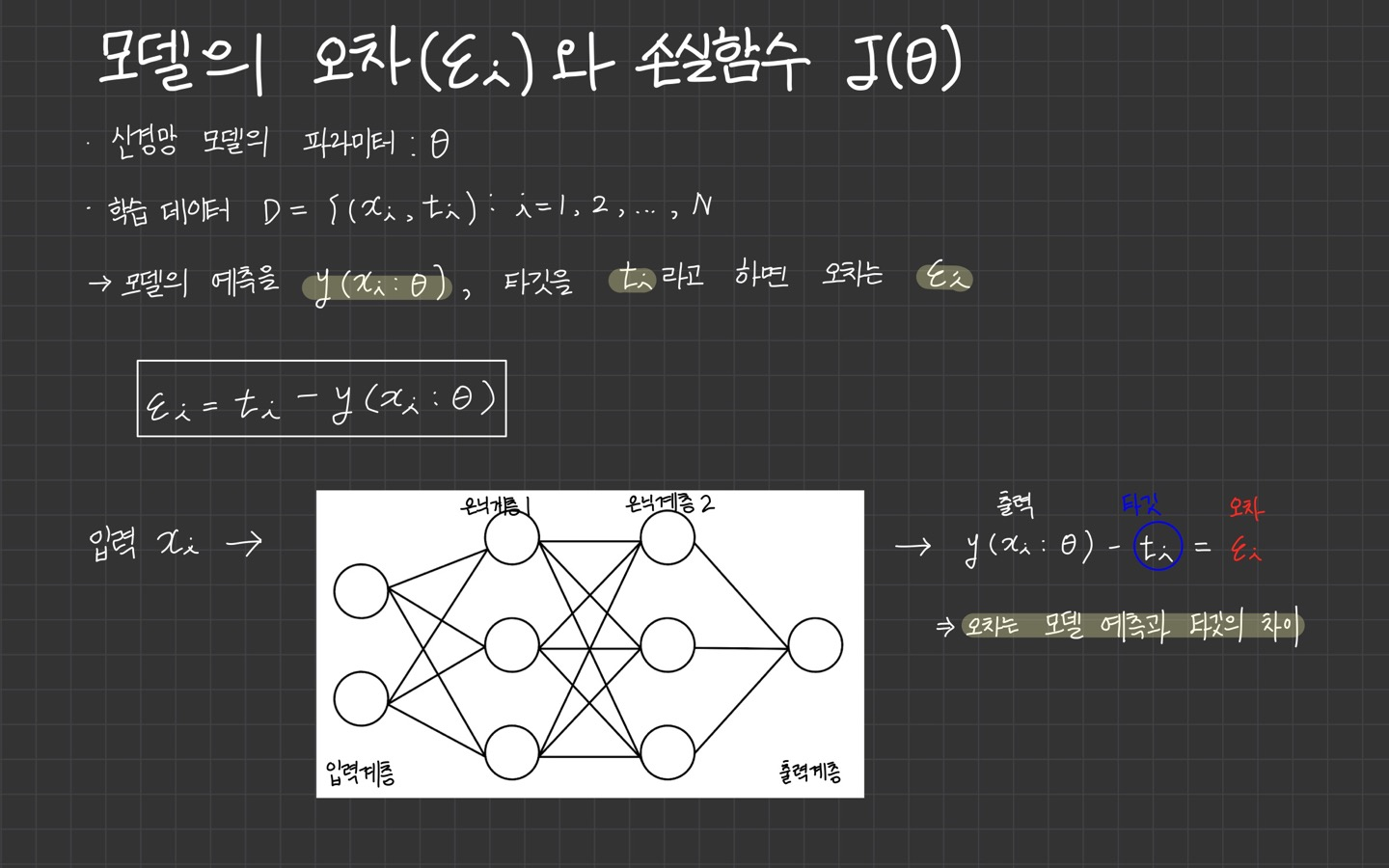
모델의 오차는 모델의 예측과 실제 타겟의 차이입니다.
손실함수의 목표가 모델의 오차를 최소화하는 것이므로 어떤 방식으로 손실 함수를 정의할 때 어떤 방식으로 오차의 크기를 측정할지만 결정하면 됩니다.
2) 최대우도추정(maximum likelihood estimation)
우도(likelihood)는 모델이 추정하는 관측 데이터의 확률을 말합니다.
모델은 손실 함수의 목표는 관측 데이터의 확률이 최대화되는 확률분포 함수를 표현해야 합니다.
이 방법은 확률 모델인 경우에만 적용할 수 있으며, 최대우도추정(MLE) 방식이라고 합니다.
대부분의 신경망 모델은 확률 모델을 가정하기 때문에 최대우도추정 방식으로 손실 함수를 유도할 수 있습니다.
두 방식은 손실 함수를 정의하는 관점은 다르지만, 손실 함수를 유도하면 동일한 최적해를 갖습니다.
위의 식은 전체 표본집합의 결합확률밀도 함수를 likelihood function이라고 합니다.
식의 결과 값이 가장 커지는 를 추정값 로 보는 것이 가장 그럴듯합니다.
결국 Maximum Likelihood Estimation은 Likelihood 함수의 최대값을 찾는 방법이라 할 수 있습니다.
2. 오차 최소화 관점에서 손실 함수 정의
먼저 손실함수 J()은 오차 의 크기를 나타내는 함수로 정의되며, 어떤 함수로 오차의 크기를 표현하냐에 따라 성질이 달라집니다.
이때 알아야 하는 개념이 Norm입니다.

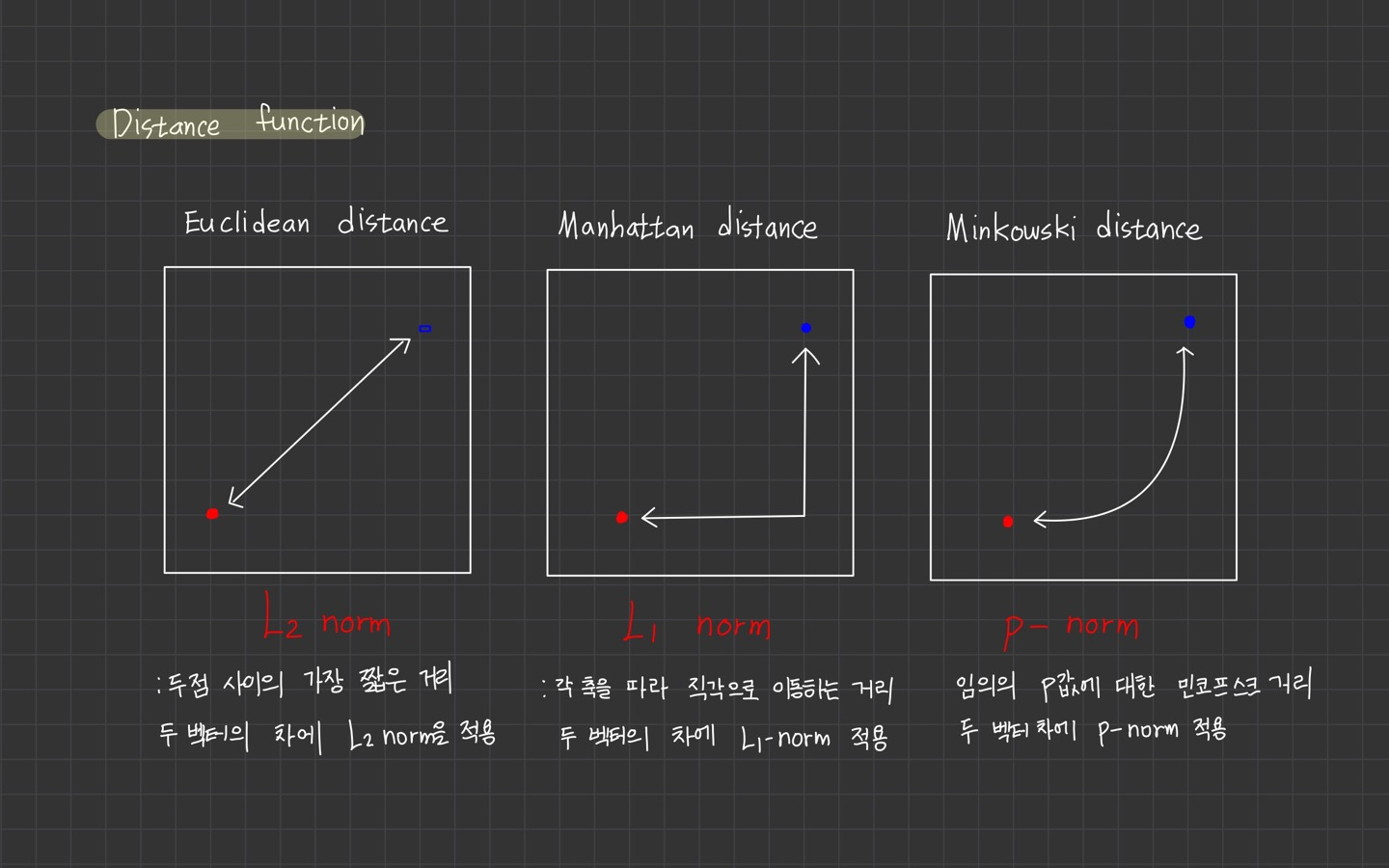
Norm에 대해서 정리를 해두었으니 참고하시길 바랍니다.
주로 과 을 사용하며, 이때 손실함수를 평균제곱오차(MSE: mean squared error), 평균절대오차(MAE: mean absolute error)라고 합니다.
지금부터 MSE, MAE에 대해 알아보겠습니다.
1) 평균제곱오차(MSE)
MSE (Mean Squared Error)
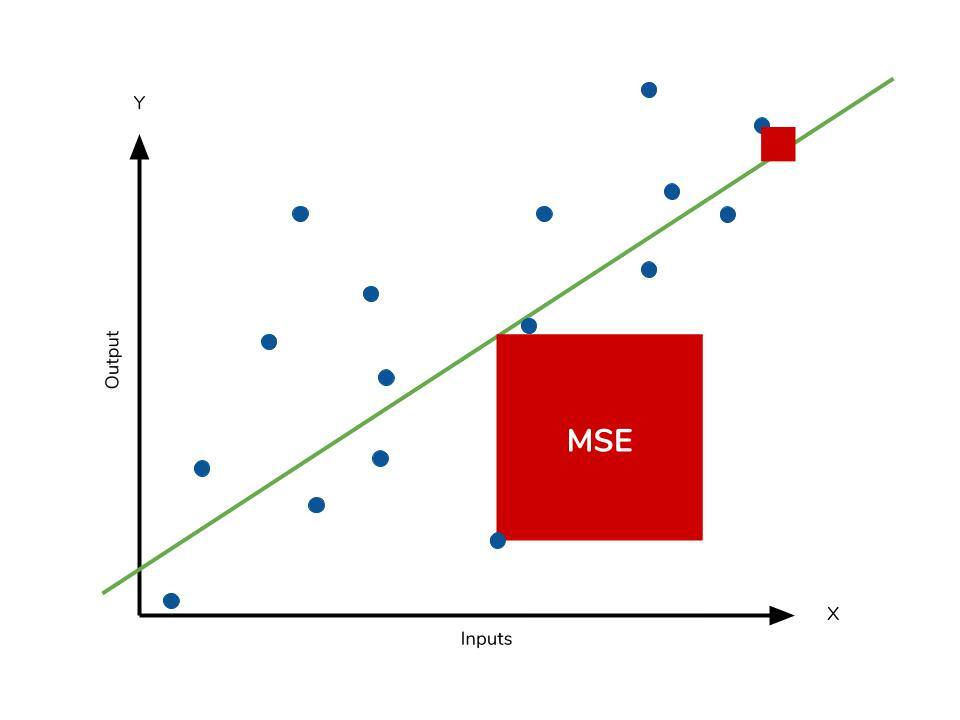
평균제곱오차는 개의 데이터에 대해 오차의 의 제곱의 평균으로 정의됩니다.
이를 라고 한다고 합니다.
평균제곱오차는 말그대로 모델이 타깃 의 평균을 예측하도록 만듭니다.
오차가 커질수록 손실이 제곱승으로 증가하므로 이상치에 민감하게 반응한다는 단점이 있습니다.
2) 평균절대오차(MAE)
MAE (Mean Absolute Error)
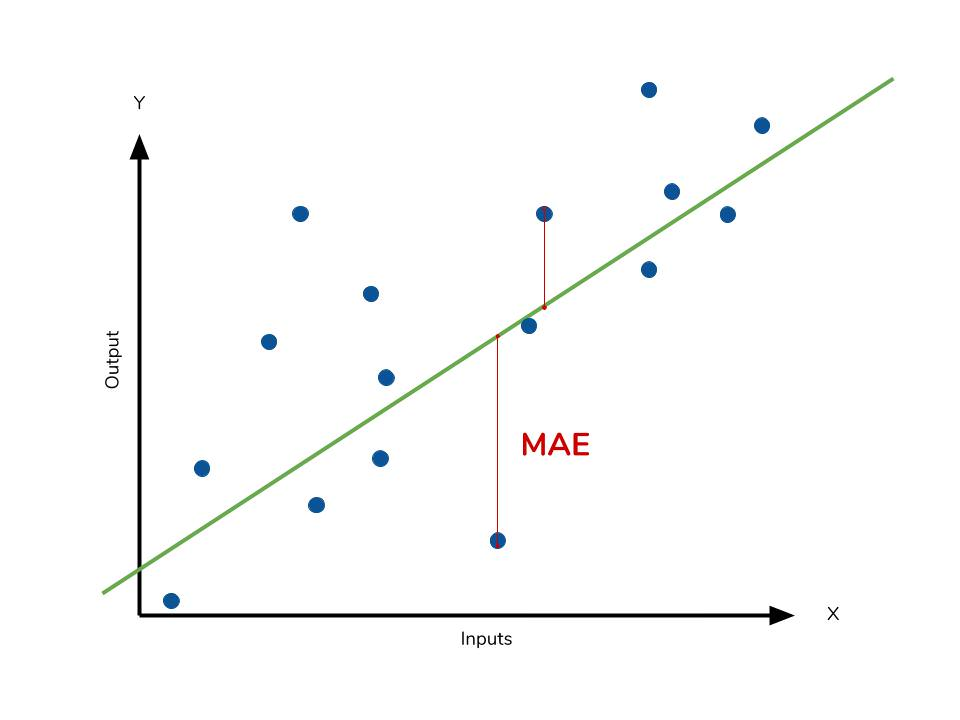
평균절대오차는 개의 데이터에 대해 오차의 의 평균으로 정의합니다.
이를 로 표기합니다.
평균절대오차는 모델이 타깃 의 중앙값을 예측하도록 만듭니다.
따라서 오차가 커질수록 손실이 선형적으로 증가하므로 이상치에 덜 민감합니다.
하지만 이는 미분가능한 함수가 아니기에 구간별로 미분을 처리해야 합니다.
*절대값을 쓰므로 미분이 불가능하다.
3) MSE vs MAE
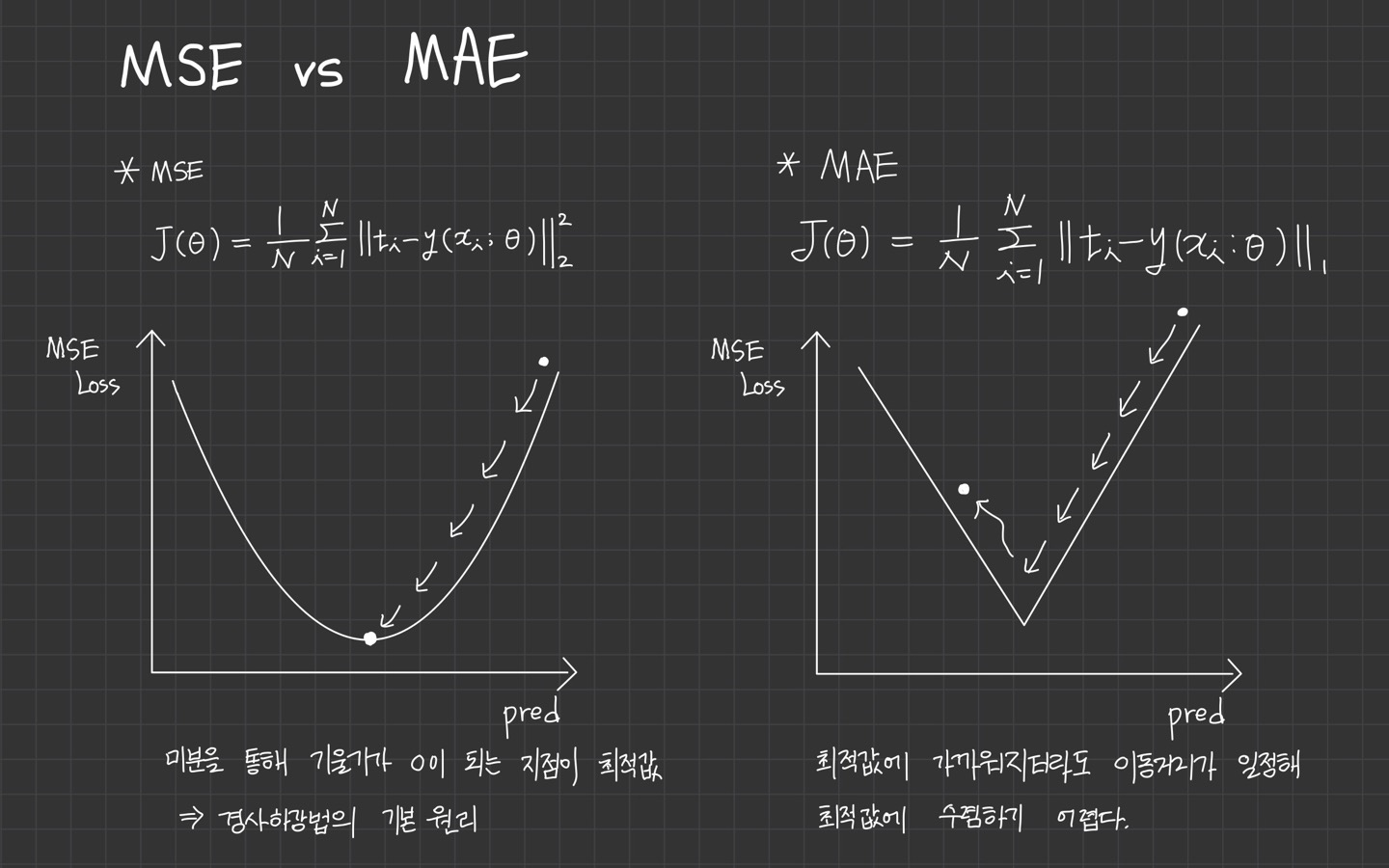
3. MLE란?
최대우도법(Maximum Likelihood Estimation)
*MLE의 경우, 위의 참고 자료 공대생의 수학정리노트를 바탕으로 정리하였습니다.
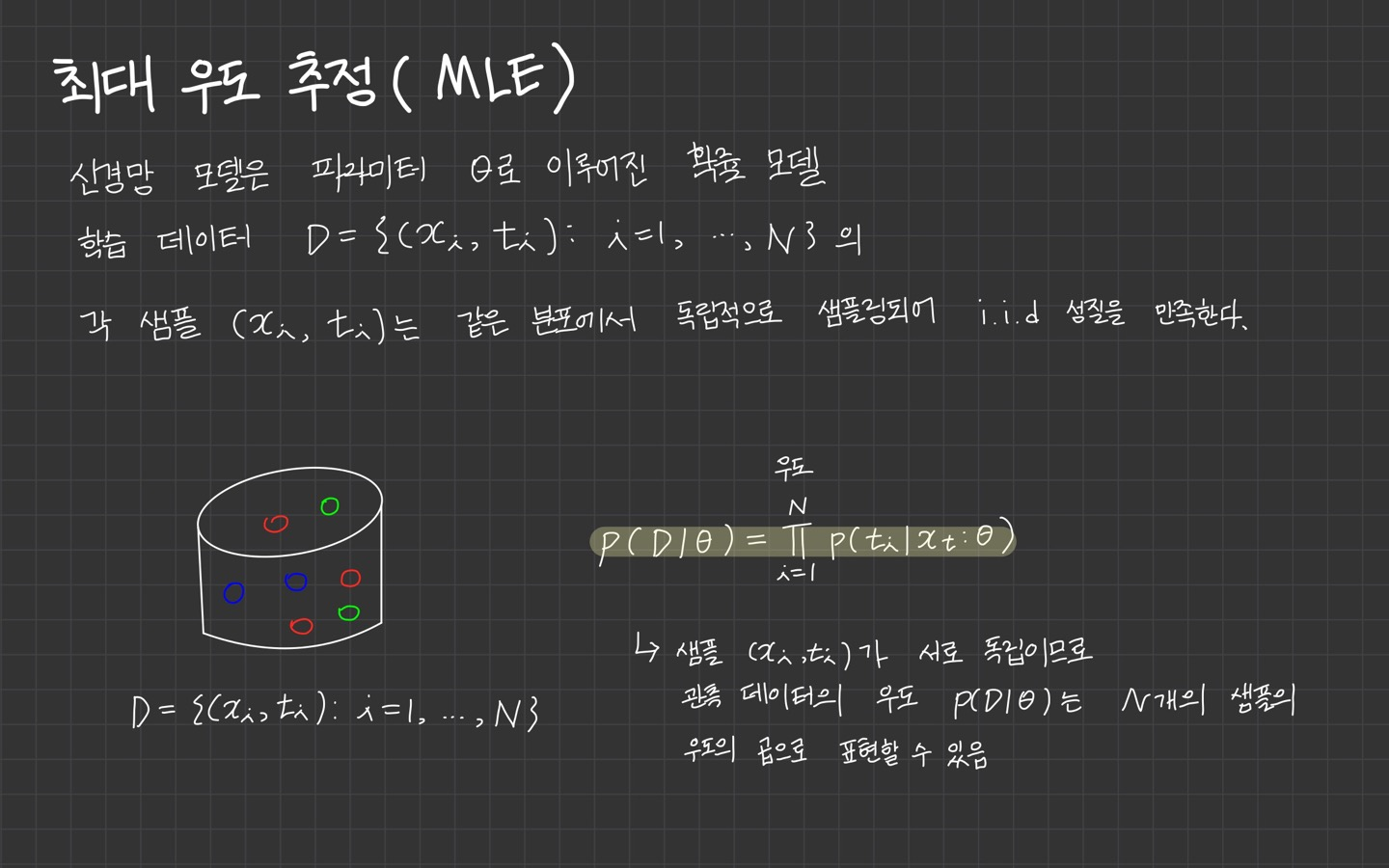
최대우도추정은 모수적인 데이터 밀도 추정 방법으로써 파라미터 으로 구성된 확률밀도 함수 에서 관측된 표본 데이터 집합을 이라 할 때 이 표본들에서 파라미터 를 추정하는 방법입니다.
위의 이미지를 통해 정리한 내용을 보면 샘플 가 서로 독립이므로 관측 데이터의 우도 는 N개의 샘플의 우도의 곱으로 나타난다고 설명되어 있습니다.
하지만 전 여기서 MLE가 이해되지 않았던 점은 왜 합()이 아닌 곱()으로 계산이 되느냐였는데요. 🥺❓
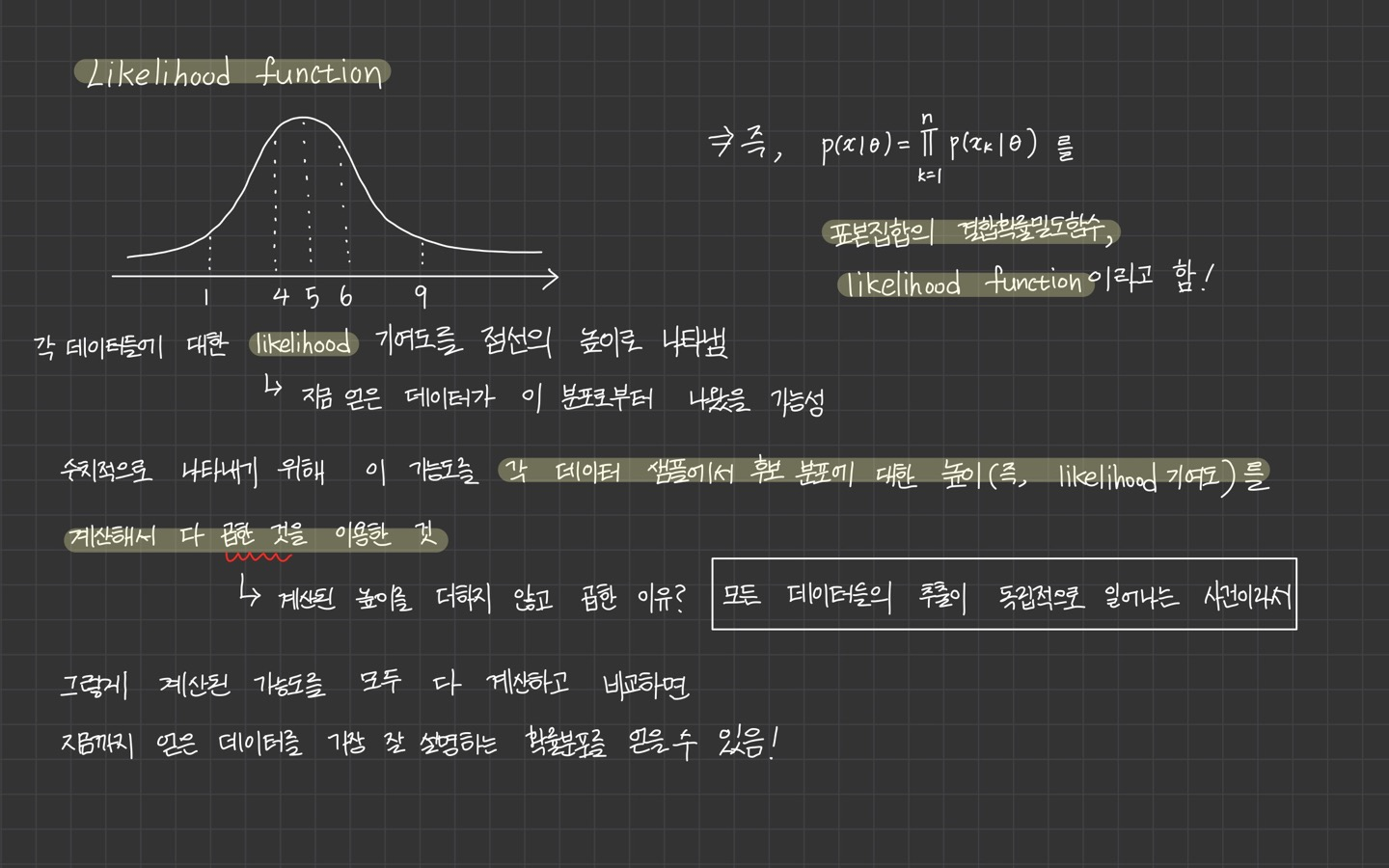
likelihood가 무엇인지, 의 식을 어떻게 해석하면 좋은지에 대해 위에 정리되어 있습니다.
위 식의 결괏값이 가장 커지는 를 추정값 으로 봐야합니다.
💡 여기서 중요한 것은 결국 likelihood function이 최대가 되어야 하며, 최대화 할 파라미터 를 찾는 문제라는 점입니다.
1) Likelihood function의 최대값을 찾는 방법

결국 Maximum Likelihood Estimation은 Likelihood 함수의 최대값을 찾는 방법입니다.
여기서 log 함수를 사용하는 이유는 log가 단조 증가 함수이기 때문에 log-likelihood function의 최댓값을 찾으나 두 경우 모두 최댓값을 찾게 해주는 정의역의 함수 입력값은 동일합니다.
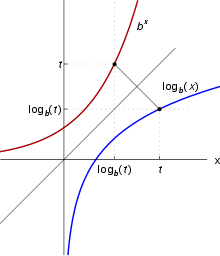
단조 증가의 의미는 함수가 정의된 구간에서 감소하지 않는 경우를 의미합니다.
위 그림에서 log 함수의 경우, 파란색 선 그래프를 의미합니다. 입력값 x가 커질수록 y도 꾸준히 증가합니다.
책에서는 로그 우도를 사용하는 이유로 세 가지를 설명하고 있는데요. (p.126-127) 3번이 위와 같은 이유를 의미합니다.
-
가우시안 분포 또는 베르누이 분포와 같은 지수 함수 형태로 표현되는 지수족(expoentail family) 확률분포의 경우 로그를 취하면 지수 항이 상쇄돼 다항식으로 변환되기 때문에 함수 형태가 다루기 쉬워진다고 합니다.
👉 이 부분은 지수함수에 로그를 취할 경우, 지수함수에 있는 지수승이 로그함수의 상수의 곱으로 내려와서 다항식으로 상쇄된다고 이해를 했는데, 틀렸다면 말씀해주세요.
-
N개의 샘플에 대한 우도의 곱을 합산으로 바꾸면 언더플로를 방지할 수 있다고 합니다. 확률은 1보다 항상 작기 때문에 확률을 N번 곱하면 N이 커질수록 언더플로가 더 심해집니다. 따라서 우도 대신 로그 우도를 사용하면 곱이 합산 형태로 바뀌므로 언더플로를 방지할 수 있습니다.
👉 여기서 생소한 개념은 언더플로였는데요. 언더플로 문제는 매우 작은 숫자를 컴퓨터에서 계산할 때 발생하는 문제라고 합니다.
정리하자면, 로그 우도(log likelihood)를 사용하는 것이 좋다!👏
왜냐하면 단조 증가의 성격을 갖고 있어서 대소 관계가 바뀌지 않습니다.
또한, 곱의 형태 식을 최대화하는 것은 어렵지만 로그를 취해서 합의 공식으로 바꿔주는 로그의 성질도 이용하여 극대화할 수 있습니다.
다시 흐름을 잃지 않기 위해, 우리는 관측 데이터 를 가장 잘 표현하는 확률 모델인 로그 우도를 최대화하는 파라미터 를 찾아야합니다!
2) 최대화 문제를 최소화 문제로 변환하는 방법
로그 우도에 음수를 취하면 됩니다! 간단...👏 로그의 성질을 이용하면 되니까 음수 부호만 붙이면 되는 것 같군요.
4. MLE 손실함수 정의
이제 거의 막바지입니다.😭 이제 손실함수를 각 아래의 문제에 따라 정의를 내려보려고 합니다.
- 회귀 문제
- 이진 분류 문제
- 다중 분류 문제
1) 회귀 문제
회귀 모델이 추정하는 가우시안 분포 는 신경망 모델이 출력한 평균 와 정밀도의 역수 를 분산으로 하는 분포로 정의됩니다.

회귀 문제는 신경망 모델을 통해 추정된 가우시안 분포의 음의 로그 우도를 손실함수로 정의합니다.

식 유도 과정은 이렇습니다. 천천히 살펴보시면 따라가실 수 있을 겁니다.
여기서 재밌었던 건 마지막에 앞에 곱해진 상수 를 1로 변경하고, 뒤의 constant를 없애주니 SSE의 식과 동일해집니다.
앞에서 보았던 평균제곱오차(MSE)와 다른 점은 를 곱한 것 밖에 없습니다.
MSE는 오차제곱합의 상수 배를 한 식이므로 둘의 최적해는 동일하다고 볼 수 있습니다.
- 상수 배는 를 의미
따라서 우도(likelihood)를 최대화하는 것은 오차를 최소화하는 것과 같습니다.
2) 이진 분류 문제

이진 분류 문제를 정의했습니다. 베르누이 분포 식을 참고해주세요.

*여기서 N은 샘플의 개수, K는 클래스의 개수를 의미합니다.
최적화 할 때는 이 식에 를 곱해서 샘플에 대한 합산 평균으로 바꿔서 사용합니다.
두 손실 함수의 최적해는 동일하지만, 평균을 사용하면 최적화 과정에서 손실이 작아지므로 수치상 안정화됩니다.
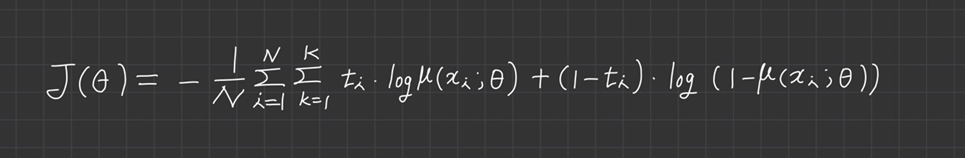
3) 다중 분류 문제
다중 분류 문제에서 최대우도추정을 위한 손실함수 정의는 다중 분류 모델이 추정하는 카테고리 분포 는 신경망 모델이 출력한 각 클래스가 발생할 확률인 로 정의됩니다.

*여기서 N은 샘플의 개수, K는 클래스의 개수를 의미합니다.
최적화 할 때는 를 곱해서 샘플에 대한 합산을 평균으로 바꿔 사용합니다.
두 손실 함수의 최적해는 동일하지만, 평균을 사용할 경우 최적화에서는 손실이 작아지므로 수치적으로 안정됩니다.
이 부분은 이진 분류 문제와 동일한 것 같습니다.
5. 신경망 학습을 위한 손실 함수
처음부터 여기까지의 과정은 신경망을 학습하기 위해 오차를 최소화하거나 우도를 최대화하는 방법을 사용하여 손실함수를 유도하기 위한 아주 긴 호흡의 과정이었습니다.
신경망 학습에 사용되는 손실 함수는 지도 학습에서 회귀 문제, 분류 문제에 따라 달라졌습니다.
- 회귀(가우시안 분포): MSE
- 분류(카테고리 분류): binary cross entropy, cross entropy
정리하며 틀린 부분은 언제나 지적 환영이며, 수고 많으셨습니다!😎
6. 추천 자료
🔗 [딥러닝] 목적/손실 함수(Loss Function) 이해 및 종류
🔗 [딥러닝 입문 5] 확률·통계의 기초(3/5)

2-2에서 MAE가 l2 loss로 표기한다는 오타가 있습니다!
그리고 4-1에서 J의 지수의 분모가 2B가 아닌 2/B가 아닌가 여쭤봅니다.!