[DL] 최적화 알고리즘 - RMSProp, Adam

공부 벌레🐛가 되자!

어제 최적화 알고리즘을 공부 중이라 하니까 어차피 Adam만 쓰는데, 굳이 다 알아야 하냐 라는 말을 들었습니다. 하지만 최근에 계속 쓰는 Adam까지 결국 왔다는 것...! 그러니까 일단 킵고잉👊

그전의 $optimizer$을 보고 싶다면

최적화 알고리즘 - SGD, Momentum, Nesterov momentum, AdaGrad

해당 게시글을 참고해주세요!

참고 자료

📕 딥러닝 교과서, 출판사: 이지스 퍼블리싱
📙 밑바닥부터 시작하는 딥러닝, 출판사: 한빛미디어
💻 Andrew Ng Exponentially Weighted Averages (C2W2L03)
💻 Andrew Ng RMSProp (C2W2L07)

💻 Andrew Ng Adam Optimization Algorithm (C2W2L08)

목차

지수 가중 이동 평균

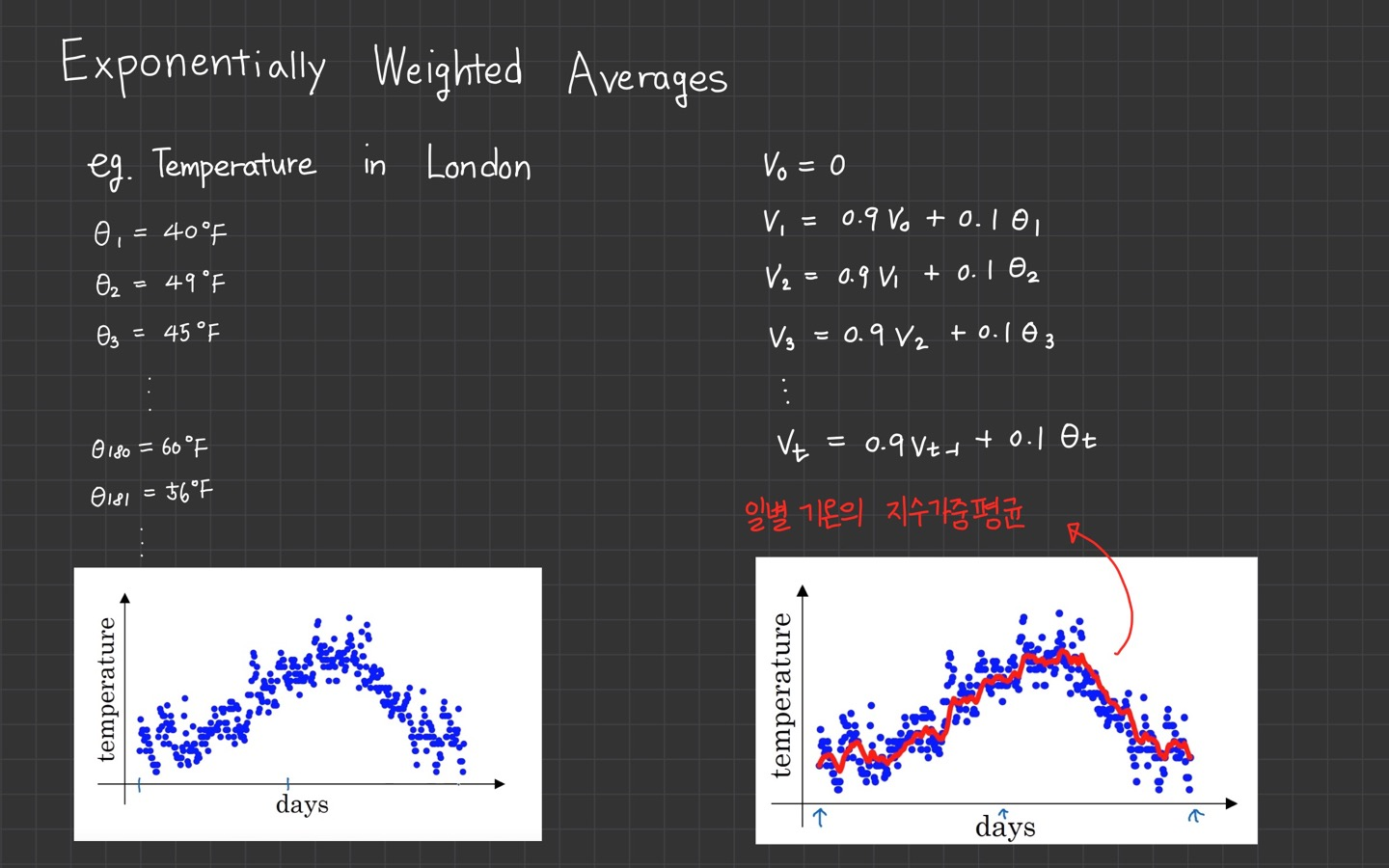
예시는 런던의 1년 일별 기온입니다.

$\theta_{1,...,365}$로 표현이 되었고 그래프에 파란색 점으로 찍혔습니다.

그리고 지수 가중 이동 평균을 구합니다.

식은 오른쪽을 참고하시면 되고

이전 기온의 지수가중이동평균에 0.9를 곱하고, 현재 기온에는 0.1을 곱합니다.

이전 값에 더 많은 가중치(0.9)를 주고, 현재 기온에는 0.1이라는 작은 가중치를 주는 방식입니다.

$V_t = \beta * V_{t-1}+(1-\beta) \theta_t$

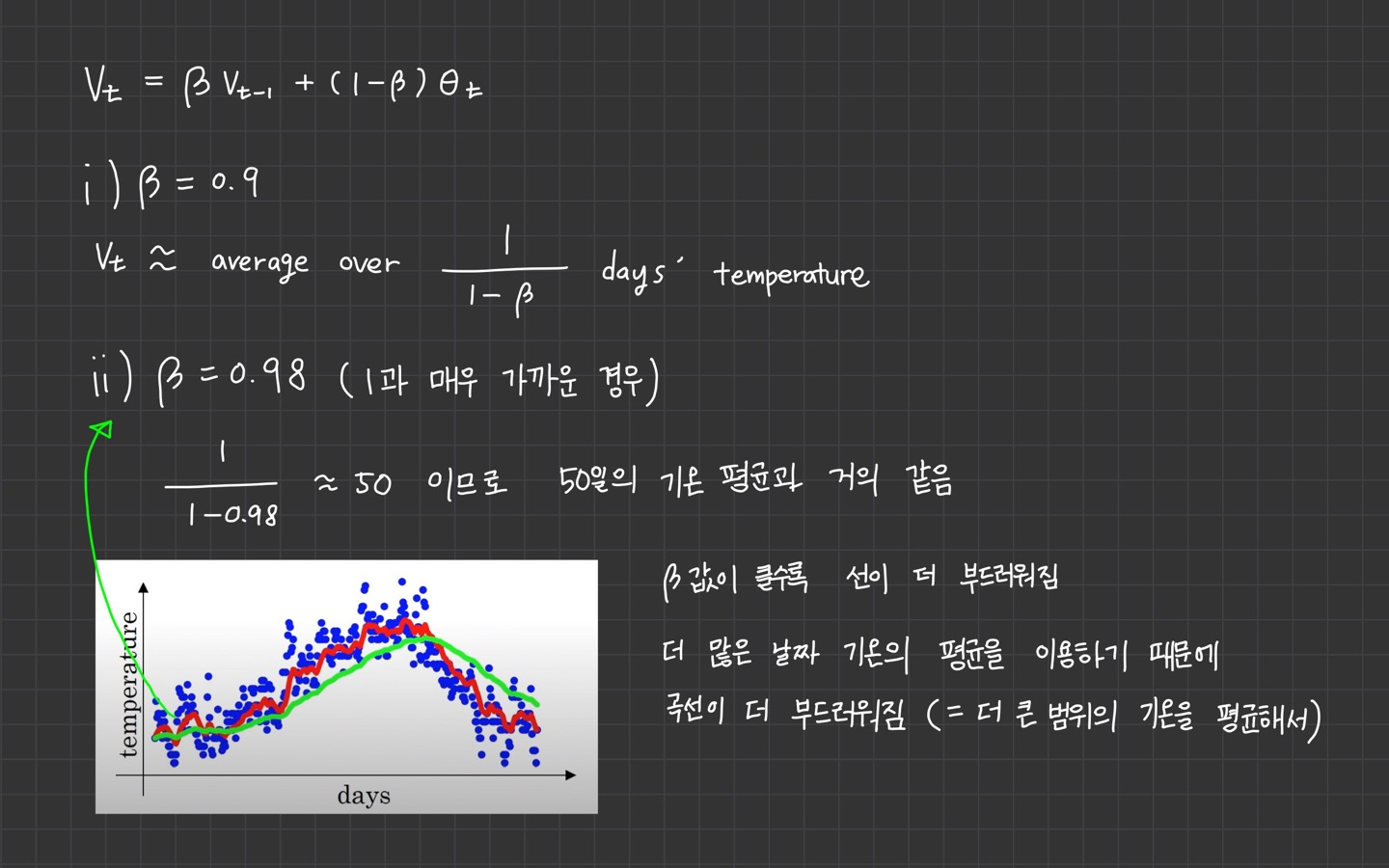
$v_t$는 $\frac{1}{1−β} 기간 동안 기온의 평균을 의미합니다.

• $β=0.9$일 때 10일의 기온 평균
• $β=0.5$일 때 2일의 기온 평균

그러나 곡선이 올바른 값에서 더 멀어집니다. 그래서 기온이 바뀔 경우 지수가중평균 공식은 더 느리게 적응합니다.

$\beta$가 0.98이면 이전 값에 많은 가중치를 주고, 현재의 기온에는 작은 가중치를 주게 됩니다.

따라서 기온이 올라가거나 내려가는데 더 느리게 반응하게 됩니다.

만약 $\beta$값을 0.5로 낮춘다면 $\frac{1}{1-\beta}$ 식에 따라 2일의 기온을 평균내는 것과 같습니다.

그렇다면 2일의 기온만 평균내서 더 노이즈가 많고 이상치에 민감한 형태가 됩니다. 기온 변화에는 더 빠르게 적응을 하게 됩니다.

$V_t = \beta * V_{t-1}+(1-\beta) \theta_t$

이 식은 Exponentially Weighted Averages(지수가중이동평균)이라 부르며,

parameter 혹은 학습 알고리즘의 hyper parameter 값을 바꾸면서 달라지는 효과를 얻게 되고 이를 통해 가장 잘 작동하는 값을 찾게 됩니다.

여기서 $β$ 값이 hyper parameter 값입니다. 보통 사용하는 값은 0.9 입니다.

이렇게 희한하게 계산되는 지수가중이동평균은 왜 쓰일까요?

지수가중이동평균은 최근 데이터에 더 많은 영향을 받는 데이터들의 평균 흐름을 계산하기 위해 구합니다. 그리고 최근 데이터 지점에 더 높은 가중치를 줍니다.

갑자기 최적화 알고리즘 공부하기 전, 지수가중이동평균을 공부한 이유는 RMSProp에서 쓰이기 때문입니다.

RMSProp

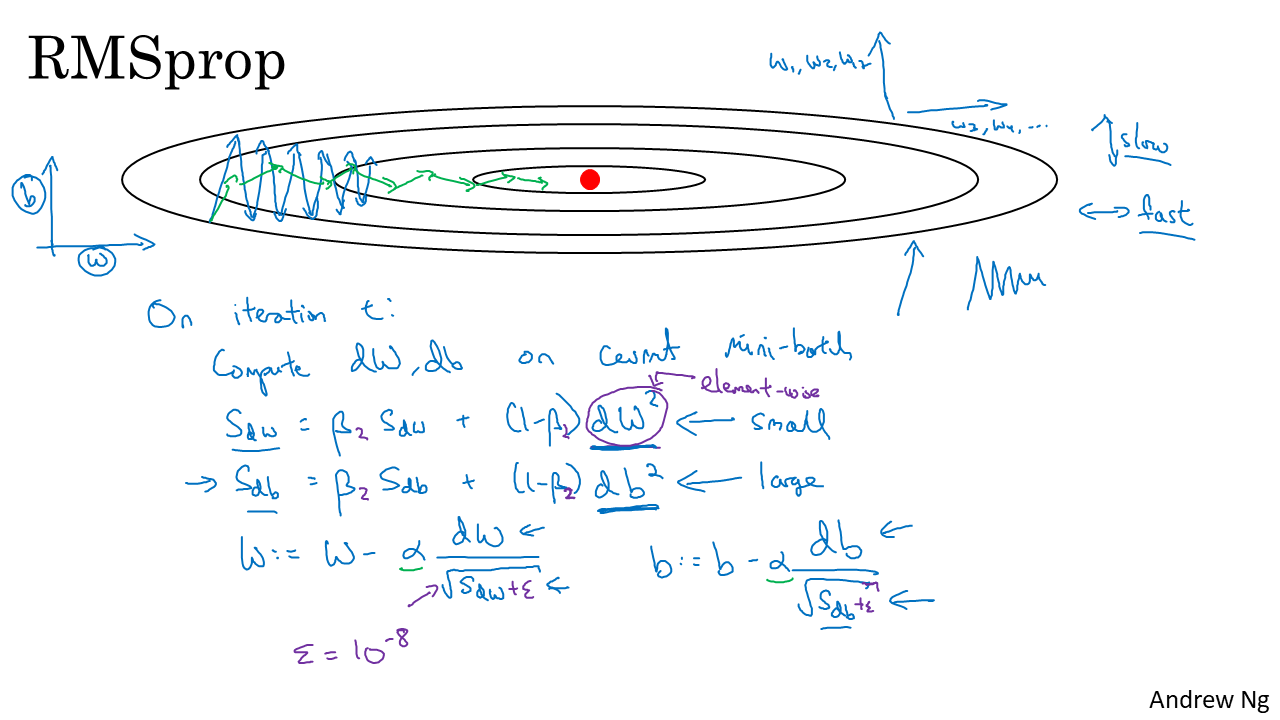
RMSProp은 AdaGrad에서 학습이 안 되는 문제를 해결하기 위해 hyper parameter인 $\beta$가 추가되었습니다.

변화량이 더 클수록 학습률이 작아져서 조기 종료되는 문제를 해결하기 위해 학습률 크기를 비율로 조정할 수 있도록 제안된 방법입니다.

RMSProp은 최근 경로의 곡면 변화량을 측정하기 위해 지수가중이동평균을 사용합니다.

RMSProp의 장점은 미분값이 큰 곳에서는 업데이트 할 때 큰 값으로 나눠주기 때문에 기존 학습률 보다 작은 값으로 업데이트 됩니다.

따라서 진동을 줄이는데 도움이 됩니다.

반면 미분값이 작은 곳에서는 업데이트시 작은 값으로 나눠주기 때문에 기존 학습률 보다 큰 값으로 업데이트 됩니다.

이는 조기 종료를 막으면서도 더 빠르게 수렴하는 효과를 불러옵니다.

따라서 최근 경로의 gradient는 많이 반영되고 오래된 경로의 gradient는 작게 반영됩니다.

gradient 제곱에 곱해지는 가중치가 지수승으로 변화하기 때문에 지수가중평균이라 부릅니다.

매번 새로운 gradient 제곱의 비율을 반영하여 평균을 업데이트 하는 방식입니다.

Adam

드디어 마지막 Adam입니다!

Adam은 Momentum과 RMSProp이 합쳐진 형태입니다.

진행하던 속도에 관성도 주고, 최근 경로의 곡면의 변화량에 따른 적응적 학습률을 갖는 알고리즘입니다.

'관성' + '적응적 학습률' = Adam

Momentum처럼 진행하던 속도에 관성을 주고, RMSProp과 같이 학습률을 적응적으로 조정하는 알고리즘

이 방법은 모멘텀이 있는 경사 하강법의 효과와 RMSProp이 있는 경사 하강법의 효과를 합친 결과가 나옵니다.

이것은 매우 넓은 범위의 아키텍처를 가진 서로 다른 신경망에서 잘 작동한다는 것이 증명되었습니다.

그래서 일반적 알고리즘에서 현재 가장 많이 사용되고 있습니다.

이 알고리즘은 출발 지점에서 멀리 떨어진 곳으로 이동하는 초기 경로의 편향 문제가 있는 RMSProp의 단점을 제거하였습니다.

천천히 살펴보겠습니다.

개념

• 1차 관성으로 속도를 계산합니다. 속도에 마찰 계수 $\rho$ 대신에 가중치 $\beta_1$을 곱해서 gradient의 지수가중이동평균을 구하는 형태로 수정되었습니다.

• 2차 관성으로 $(gradient)^2$의 지수가중이동평균을 구합니다.

• 마지막은 parameter 업데이트 식으로 1, 2차 관성을 사용합니다.

초기 경로에서 편향이 발생하는 이유

훈련을 시작할 때 1차 관성 $v_0$, 2차 관성 $r_0$ 모두 0으로 초기화합니다.

이 상태에서 첫 번째 단계를 시행하면

각각 0.1, 0.01이 곱해져서 값이 작아집니다.

$r_1$이 작아지면 적응적 학습률이 커져 출발 지점에서 멀리 떨어진 곳으로 이동하게 되고,

최적해에 도달하지 못할 수도 있습니다.

그래서 도입한 방법이 해당 방법입니다. 이렇게 알고리즘을 개선했을 때,

식이 상쇄되기 때문에 $r_1$은 $(gradient)^2$이 되어 아주 작아질 일이 없습니다.

이 방법으로 학습 초반에 학습률이 급격히 커지는 편향이 제거되고, 훈련이 진행될 수록 $(1-\beta^t_1)$와 $(1-\beta^t_2)는 1에 수렴하므로 원래 알고리즘 형태로 돌아옵니다.

수식에 대한 이해가 어렵다면 그냥 넘어가도 될듯 하옵니다.

hyperparameter

이때까지 본 optimizer와 비교해서 Adam이 가장 특별한 점은 이 hyper parameter 값이 많다는 점인데요.

하나씩 살펴보겠습니다.

• $\alpha$:학습률. 매우 중요하고 보정될 필요가 있으므로 다양한 값을 시도해서 잘 맞는 값을 찾아야 합니다.
• $\beta_1$: 기본적으로 0.9를 사용. 모멘텀에 관한 항
• $\beta_1$: 기본적으로 0.99나 0.999를 이용(논문에서는 0.999를 추천)
• $\epsilon$: Adam 논문에서는 $10^{-8}$을 추천. 분모가 0이 되는 것을 막기 위해 더해주는 상수. 하지만 이 값을 설정하지 않아도 전체 성능에는 영향이 없습니다.

보통 $\beta_1$, $\beta_2$, $\epsilon$의 세 가지 값은 고정 시켜두고, $\alpha$을 여러 값을 시도해가면서 가장 잘 작동되는 최적의 값을 찾습니다.

Adam은 Adaptive moment estimation에서 온 용어입니다.

$\beta_1$이 도함수의 평균을 계산하므로 첫 번째 momentum이고,

$\beta_2$는 지수가중평균의 제곱을 계산하므로 두 번째 momentum입니다.

이 모두를 Adma optimizer algorithm라 부릅니다.

이 분의 성함은 Adam Coates입니다. Andrew Ng 교수님의 오랜 친구이자 동료라고 하네요.

이분이 바로 Adam 알고리즘을 만든 사람...

같지만 '그가 이 알고리즘을 사용하기는 하지만 그와는 아무 상관이 없습니다.'라고 설명하십니다.

Adam까지 optimizer를 살펴보았습니다!

모두 고생하셨습니다.👊