[DL] 회귀 모델 (Regression Model)

이번 포스팅은 머신러닝의 지도학습 중 분류와 회귀로 나뉘는 개념 중 회귀에 대해 간단히 정리해보려고 합니다.

분류 문제는 범주형 데이터를 예측하는 문제이며, 회귀 문제는 숫자형 데이터를 예측하는 문제입니다.

회귀 문제는 여러 독립 변수와 종속 변수의 관계를 연속 함수 형태로 분석하는 문제인데요.

데이터를 관측할 때 발생하는 관측 오차 및 실험 오차를 가우시안 분포(Gaudssian distribution)로 정의되므로 회귀 문제는 가우시안 분포를 예측하는 모델로 정의할 수 있습니다.

가우시안 분포(Gaudssian distribution)

가우시안 분포는 정규 분포, 가우시안 정규 분포 등의 이름으로 동일하게 불리는 것 같습니다.

평균을 중심으로 대칭적인 종 모양의 사건이 발생할 확률을 나타내며

식은

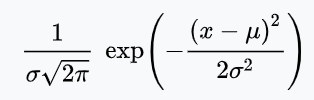
이렇게 정의합니다.

$x$가 확률 변수, $μ$는 평균, $σ^2$는 분산, $σ$는 표준 편차입니다.

관측 데이터의 분포를 근사하는 데에 자주 쓰인다고 생각하시면 됩니다.

중심 극한 정리에 따라 독립적인 확률 변수들의 평균은 가우시안 분포에 가까워지는 성질이 있습니다.

📌참고 중심 극한 정리

회귀 모델 정의

관측 데이터는 $D=${$(x_i, t_i): i=1,...,N$}으로 N개의 $(x_i, t_i)$ 샘플로 구성됩니다.

입력 데이터 $x_i$는 같은 분포에서 독립적으로 샘플링 되어 독립을 만족하고,

타깃 $t_i$는 모델 예측값 $y(x_i: Θ)$에 관측 오차 $ε$가 더해진 값으로 정의되며

관측 오차 $ε$는 가우시안 분포 $N(ε|0, B^{-1})$를 따른다고 가정합니다.

이때 오차의 분산 $B^{-1}$은 정밀도(precision) $β$의 역수로 상수로 가정합니다.

분산과 정밀도는 서로 역수 관계입니다. 즉, 분산이 크면 정밀하지 않은 것으로 생각하고, 분산이 작으면 정밀한 것으로 생각할 수 있습니다.

타겟은 다차원 공간의 연속 함수에 있는 한 점이라 생각하면 되고, 실수 벡터로 표현합니다.

이 타깃들의 분포가 가우시안 분포가 되는 겁니다.

$t_i$ = $y(x_i: Θ)$ + $ε$, $ε$~ $N(ε|0, B^{-1})$

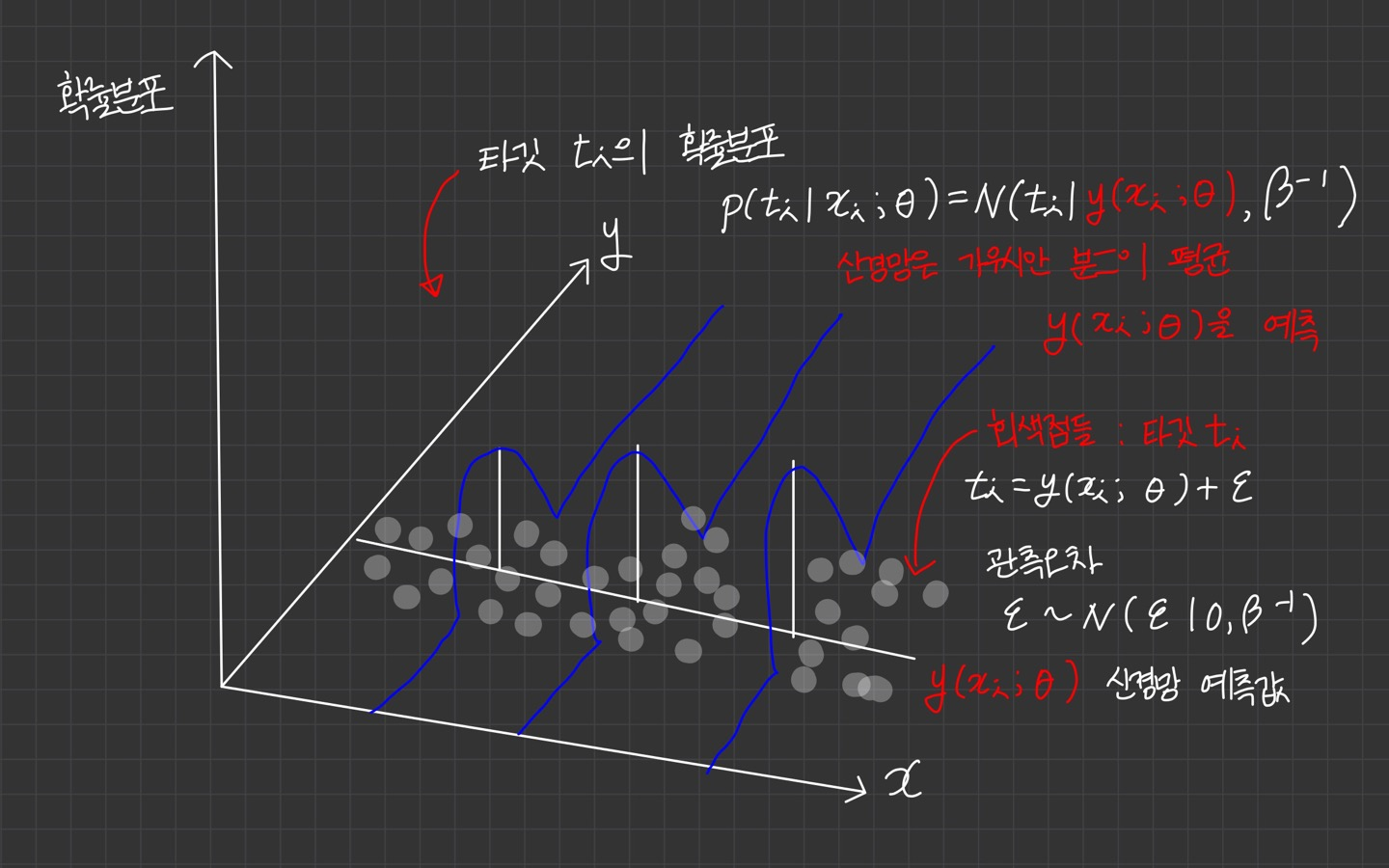
위 그림의 회색 점은 관측 데이터의 타깃 $t_i$입니다.

입력 $x_i$마다 관측 데이터인 타깃 $t_i$가 달라집니다.

예를 들어, $x_i$를 집값을 예측하기 위한 입력인 '방 3개, 32평, 아파트, 역과의 거리 20분 거리' 등이라 하면 회색 점들은 집값 관측 데이터인 $t_i$입니다.

따라서 동일한 입력마다 여러 회색 점들이 존재하므로 집값의 분포를 이루게 됩니다.

따라서 회귀 모델은 입력 $x_i$가 주어졌을 때 타깃 $t_i$의 조건부 확률분포인 $p(t_i|x_i; θ)$를 예측합니다.

관측 오차 $ε$는 가우시안 분포로 가정했기 때문에 타깃 $t_i$의 분포는 관측 오차의 분산 $B^{-1}$를 갖는 가우시안 분포로 정의됩니다.

따라서 신경망 모델은 평균 $y(x_i; θ)$만 예측하면 됩니다.

$p(t_i|x_i; θ)$ =$N(t_i|y(x_i:θ), B^{-1})$

출력 계층의 활성 함수

집값을 결정하는 요인으로 구성된 '방의 개수, 면적, 집 종류, 역과의 거리' 데이터로 집값을 예측하는 회귀 모델을 만든다고 해봅시다.

모델은 입력 데이터로 집값의 가우시안 분포의 평균인 $μ$를 예측합니다.

회귀 모델의 경우, 예측된 평균과 분산이 바뀌면 안 되기 때문에 항등 함수를 활성 함수로 사용합니다.