Super Resolution 결과 평가 - PSNR, SSIM

미남로그·2021년 9월 14일

Super Resolution 결과가 얼마나 좋은지 많은 연구들에서 사용되는 정량적인 평가 척도가 몇 가지 있습니다. 이러한 척도에 대해 간략하게 알아보겠습니다.

그리고 이를 활용해 앞서 진행한 SRCNN과 SRGAN 모델 각각이 만들어낸 고해상도 이미지를 비교해 봅시다!

PSNR과 SSIM

MSE(Mean Squre Error)

MSE는 몇 번 들어보셨을 듯! 평균 제곱 오차입니다. 그러니까 오차에 제곱에 대해 평균을 취한 값입니다.

그러면 값이 작을 수록 오차가 작은 거라 생각할 수 있겠죠? 그래서 값이 작을 수록 정확성이 높다고 볼 수 있습니다.

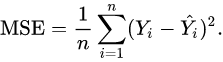
식은 이렇습니다.

오차는 classification 보다 선형회귀에서 더 주로 쓰입니다. 예측 값과 라벨의 오차를 제곱값으로 처리하여서 학습하도록 돕스니다.

MSE를 설명한 이유는 PSNR에 MSE가 쓰이기 때문입니다.

PSNR(Peak Signal-to-Noise Ratio)

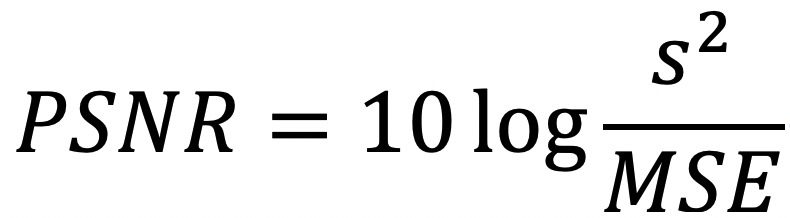
MSE가 분모로 들어갔습니다. 그러면 MSE 값이 적을 수록 좋았던 것이니까 PSNR은 값이 클수록 더 좋겠네요.

s는 영상에서 픽셀의 최대값입니다. 8bit unsigned integer 인 경우 255가 되고, double 이나 float type으로 소수점 형태로 표현될 경우 1이 됩니다.

PSNR은 영상 내 신호가 가질 수 있는 최대 신호에 대한 잡음(noise)의 비율을 나타냅니다. 일반적으로 영상을 압축했을 때 화질이 얼마나 손실되었는지 평가하는 목적으로 사용됩니다. 데시벨(db) 단위를 사용하며, PSNR 수치가 높을수록 원본 영상에 비해 손실이 적다는 의미입니다 (값이 높을수록 좋습니다).

하지만 해당 글에서 먼저 정량적 평가 지표를 살펴본 적이 있었습니다.

바로 이 이미지였는데요. 앞이 PSNR 값을 의미합니다. 하지만 사람의 눈에는 결과1보다 결과2가 더 선명하고 고해상도라고 느껴집니다.(사람마다 다르겠지만)

중요한 점은 PSNR은 인간이 시각적으로 느끼는 품질 차이를 표현한 방법이 아니라는 것입니다. 사람의 눈으로 보았을 때는 결과 2가 더 좋지만 결과 1이 더 좋은 결과를 보여주는 것처럼요.

또, MSE가 0이 되는 경우가 있습니다. 이것은 무엇을 의미할까요?

MSE가 0이 되면 PSNR이 정의 될 수 없다고 합니다. PSNR의 식을 다시 봅시다.

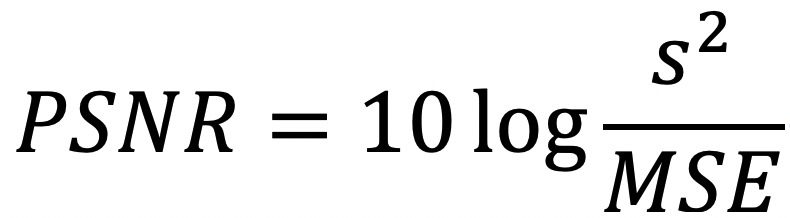
MSE는 분모에 들어가 있기 때문에, 분모에는 0이 들어갈 수 없어서 값을 정의내릴 수 없습니다. 0이 되는 것도 아닙니다.

이 경우에 실제로 PSNR 값은 inf로 출력됩니다. 이는 비교할 두 영상이 동일하다는 의미와 같다고 생각하면 됩니다. MSE가 두 영상 간의 각각의 픽셀 값 간의 차이를 계산하기 때문입니다.

SSIM(Structural Similarity Index Map)

SSIM은 PSNR과 다르게 수치적인 에러가 아닌 인간의 시각적 화질 차이를 평가하기 위해 고안된 방법입니다. 사람의 시각은 이미지 구조 정보를 도출하는데 특화되어 있어서 구조 정보의 왜곡되는 정도가 지각에 큰 영향을 미친다는 것이 SSIM의 핵심적 가설이었습니다.

SSIM은

Luminance(휘도)
Contrast(대비)
Structural(구조)

이 3가지 측면에서 품질을 평가합니다.

먼저, SSIM의 전체 수식을 살펴보면 <그림 3>과 같습니다.

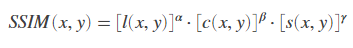
l이 1번, c가 2번, s가 3번이 됩니다.

각각의 함수식을 살펴보겠습니다.

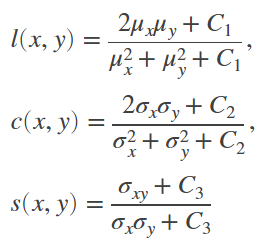
원본 이미지 x와 왜곡 이미지 y가 있다고 할 때, SSIM은 두 이미지의 휘도, 대비 및 구조를 비교합니다.

이렇게 세 가지 항목을 묶어서 품질 맵을 이미지 x, y의 상관계수를 구하는 방식으로 이미지를 비교합니다.

영상의 구조 정보를 고려하여 얼마나 구조 정보를 변화시키지 않았는지를 계산합니다. 특정 영상에 대한 SSIM값이 높을수록 원본 영상의 품질에 가깝다는 의미입니다. (마찬가지로 값이 높을수록 좋습니다).

개념 정리

PSNR은 인간이 시각적으로 느끼는 품질 차이를 표현한 방법이 아니다.
SSIM은 PSNR과 다르게 수치적인 에러가 아닌 인간의 시각적 화질 차이를 평가하기 위해 고안된 방법이다.
PSNR, SSIM 값 둘 다 높아야 좋다.

PSNR, SSIM 계산

두 값은 scikit-image 라이브러리를 이용해 쉽게 계산할 수 있습니다.

from skimage import data
import matplotlib.pyploy as plt

hr_cat = data.chelsea() # skimage에서 제공하는 예제 이미지를 불러옵니다.
hr_shape = hr_cat.shape[:2]

print(hr_cat.shape) # 이미지의 크기를 출력합니다.

plt.figure(figsize=(8,5))
plt.imshow(hr_cat)

(300, 451, 3)
<matplotlib.image.AxesImage at 0x7f407544bc50>

이 고양이 또 만났습니다. 😺😺 이 이미지로 PSNR과 SSIM을 계산해보겠습니다.

여기서는 peak_signal_noise_ratio , structural_similarity 두 메서드를 이용합니다.

from skimage.metrics import peak_signal_noise_ratio, structural_similarity

print("**동일 이미지 비교**")
print("PSNR :", peak_signal_noise_ratio(hr_cat, hr_cat))
print("SSIM :", structural_similarity(hr_cat, hr_cat, multichannel=True))

**동일 이미지 비교**
PSNR : inf
SSIM : 1.0

이번엔 고양이의 가로 세로 픽셀 수를 각각 1/2, 1/4, 1/8로 줄이고, bicubic interpolation을 이용해 원래 크기로 복원해 보겠습니다. 각각 처리된 이미지에 대해 원본 이미지와의 PSNR과 SSIM을 계산하고 그 결과를 제목으로 표시해 보겠습니다.

import cv2

# 이미지를 특정 크기로 줄이고 다시 늘리는 과정을 함수로 정의합니다.
def interpolation_xn(image, n):
    downsample = cv2.resize(
        image,
        dsize=(hr_shape[1]//n, hr_shape[0]//n)
    )
    upsample = cv2.resize(
        downsample,
        dsize=(hr_shape[1], hr_shape[0]),
        interpolation=cv2.INTER_CUBIC
    )
    return upsample

lr2_cat = interpolation_xn(hr_cat, 2) # 1/2로 줄이고 다시 복원
lr4_cat = interpolation_xn(hr_cat, 4) # 1/4로 줄이고 다시 복원
lr8_cat = interpolation_xn(hr_cat, 8) # 1/8로 줄이고 다시 복원

images = [hr_cat, lr2_cat, lr4_cat, lr8_cat]
titles = ["HR", "x2", "x4", "x8"]

# 각 이미지에 대해 PSNR을 계산하고 반올림합니다.
psnr = [round(peak_signal_noise_ratio(hr_cat, i), 3) for i in images]
# 각 이미지에 대해 SSIM을 계산하고 반올림합니다.
ssim = [round(structural_similarity(hr_cat, i, multichannel=True), 3) for i in images]

# 이미지 제목에 PSNR과 SSIM을 포함하여 시각화 합니다. 
plt.figure(figsize=(16,10))
for i in range(4):
    plt.subplot(2,2,i+1)
    plt.imshow(images[i])
    plt.title(titles[i] + f" [{psnr[i]}/{ssim[i]}]", fontsize=20)