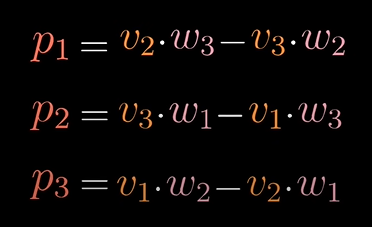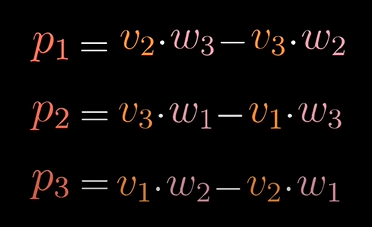
강의 바로 보러가기 클릭
Chapter 11
Cross products in the light of linear transformations
이번 챕터 11을 공부하기 위해서 선행 학습이 되어야 하는 부분이 있습니다.
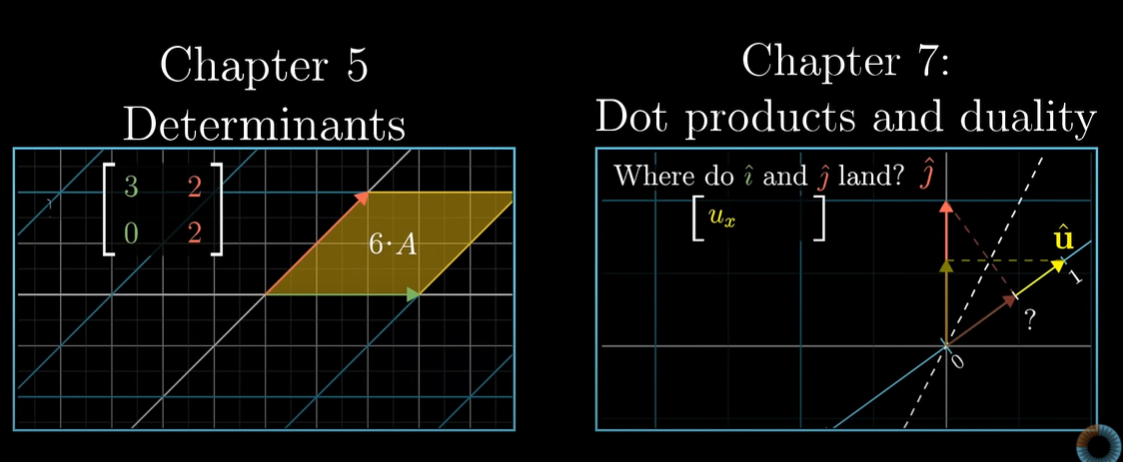
바로 행렬식을 다룬 Chapter 5. Determinants와 내적과 이중성을 다룬 Chapter 7. Dot products and duality입니다.
Chapter 5 👉 보러가기
Chapter 11 👉보러가기
짧게 복습하고 가겠습니다!
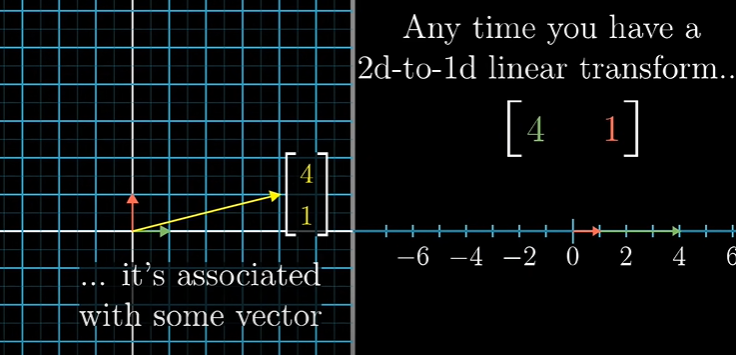
Duality(이중성)이란 어떤 공간을 수선(number line)으로 선형변환 할 때마다 그 공간의 한 특정 벡터와 연관을 가졌습니다.
선형 변환을 수행하는 것이 그 특정 벡터의 내적을 구하는 것과 같다는 의미입니다.
수치적으로 이것은 하나의 변환이 하나의 행이 있는 행렬로 설명되며, 각 열은 기저벡터가 변환된 숫자를 알려줍니다.
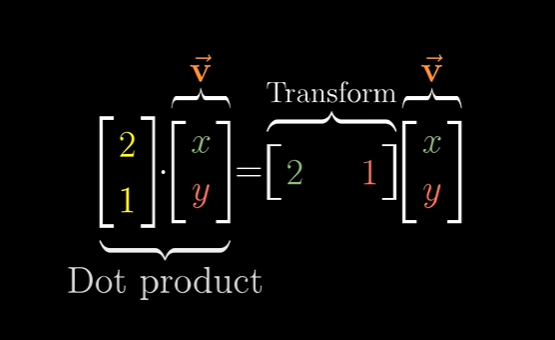
그리고 이 행렬에 어떤 벡터 v를 곱하면 계산적으로는 v와 그 행렬을 옆으로 돌려서 앋은 벡터의 내적을 구하는 것과 동일합니다.
이젠 수선(number line)에 대한 선형 변환을 발견할 때마다 그 변환을 'Dual vector(이중 벡터)'라고 불리는 어떤 벡터와 일치시킬 수 있습니다. 그래서 선형변환의 수행은 그 벡터의 내적을 얻는 것과 같습니다.
The plan
오늘의 학습 과정은 이렇다고 합니다.

- 3차원에서 수선으로의 선형변환을 정의하는 것 - 그것은 두 벡터 v, w로 정의됩니다.
- 변환을 3D 공간에서 이중 벡터로 연결 시킵니다.
- 그 이중 벡터는 v, w의 외적이 됩니다.

그러면 오늘은 기하학적 의미와 계산 사이의 관계를 명확히 이해가 될 것입니다.
Determinants
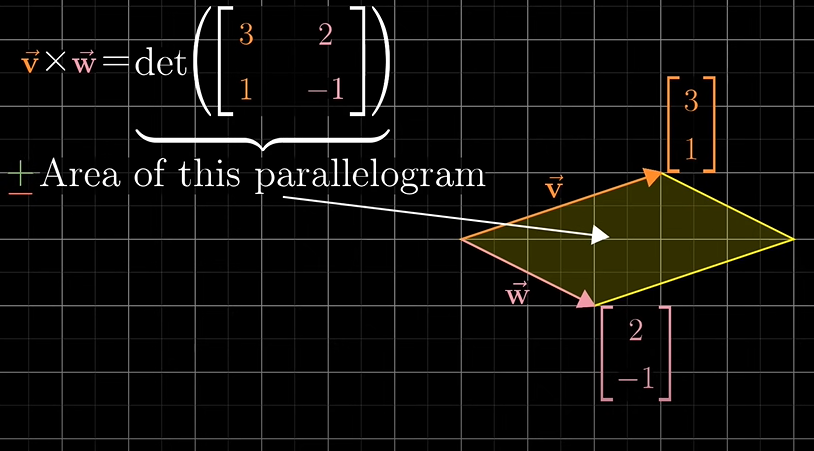
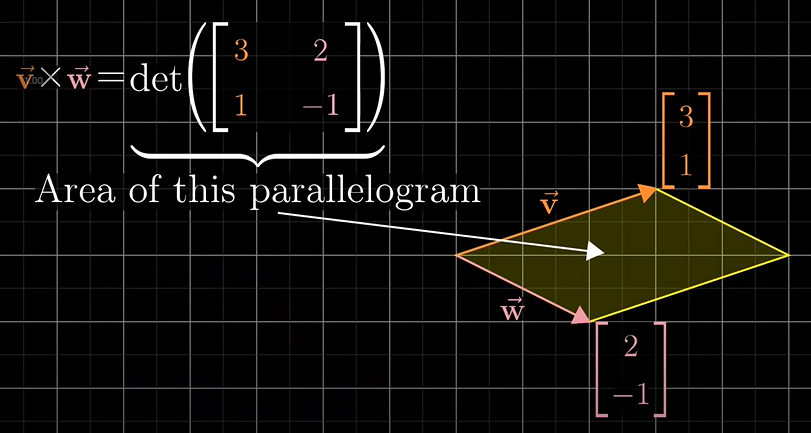
행렬식은 두 벡터에 의해 형성된 평행 사변형의 영역을 제공합니다. 그리고 두 벡터의 방향에 따라 양수/음수가 결정되었습니다.
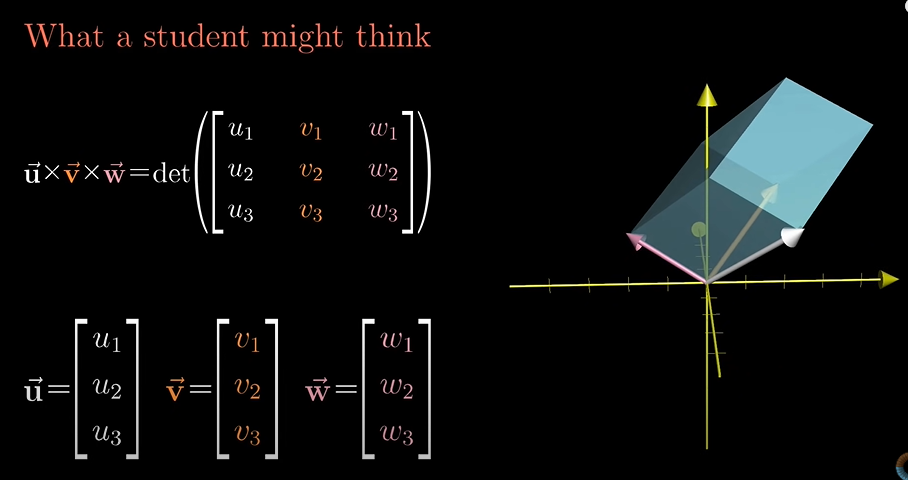
3차원은 이렇게 행렬식을 구성하고 생각할 수 있습니다. 기하학적으로 세 벡터에 의해 만들어진 평행 육면체의 부피가 됩니다.
위 식은 외적은 아닙니다. 하지만 진짜 외적이 무엇인지 가까이 다가갈 수 있게 합니다.
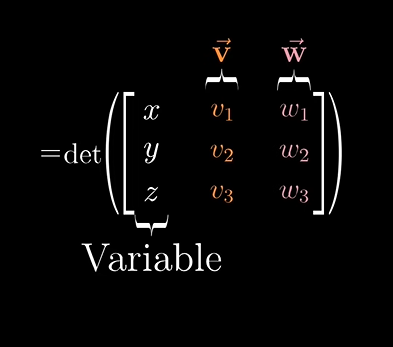
위의 식에서 x,y,z는 변수이고 v, w는 고정된 채로 남아 있습니다.
그러면 3차원에서 수선으로 가는 함수를 생각할 수 있습니다.
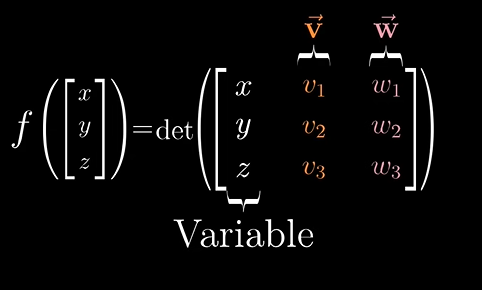
어떤 함수에 벡터 [x,y,z]를 입력하면 첫 번째 열이 x, y, z이고 다른 두 열이 상수 벡터 v, w의 좌표인 행렬의 행렬식을 얻습니다.
이 함수의 의미는 벡터 [x,y,z]에 대해 벡터 v와 w에 의해 정의된 평행 육면체입니다.
이 함수에 관해 중요한 사실은 이것이 선형이라는 점입니다.
벡터 p와 [x,y,z]의 내적
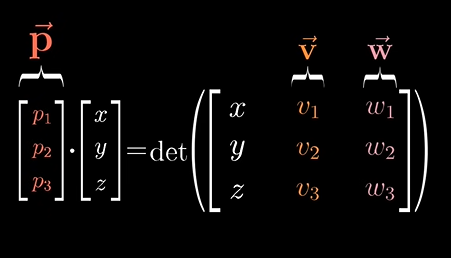
이 식을 풀어쓴다면
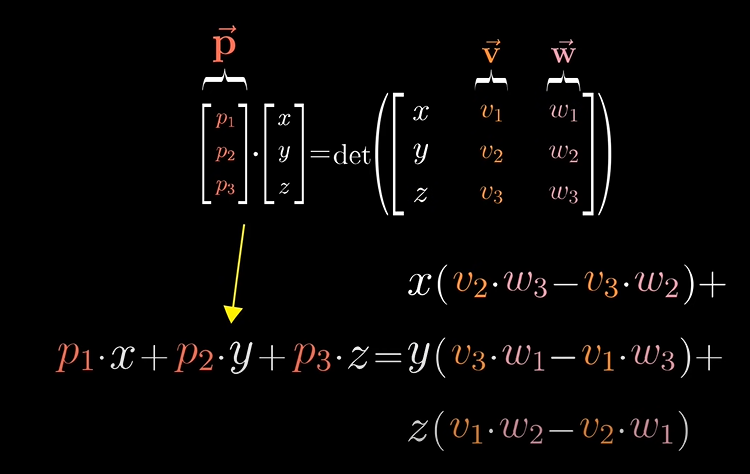
이와 같습니다.
상수들은 벡터 v와 w의 성분들에 대한 특정 조합입니다. 그래서 그 상수들 즉, v와 w좌표의 그 특별한 조합들은 찾아야 하는 벡터 p의 좌표가 됩니다!
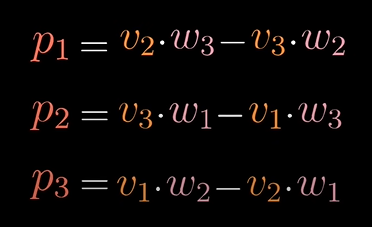
벡터 p의 속성
벡터 p와 다른 어떤 벡터 [x,y,z]의 내적을 구한 것과 벡터 v, w, [x,y,z]로 정의된 평행 육면체의 부피와 같아지는 벡터 p는 무엇인가?
주어진 벡터에 대해 선형 함수가 작동하는 방식은 주어진 벡터 v와 w에 모두 수직인 선에 투사하여 그 투사된 길이를 v와 w에 의해 정의된 평행 사변형의 면적에 곱하는 것입니다.
이제 p가 무엇인지 알 수 있을 것 같습니다.
p와 어떤 벡터 [x,y,z]의 내적을 구하는 것은 [x,y,z]와 v,w의 좌표를 열로 가지는 3x3 행렬의 행렬식을 구하는 것과 같습니다.