[최적화] Convex optimization problem

Reference

• Stanford slide
• Affine set

Convex optimization problem

Convex optimization problem
: f(x)가 convex이고 feasible set이 convex인 경우를 convex optimization problem이라 부른다.

Affine set

Affine set은 점(point), 직선(line), 평면(plane), 초평면(hyperplane)과 같이 선형적 특성이 있으면서 경계가 없는 집합을 의미합니다.

어떤 집합이 affine set이라고 말하려면 집합에 속한 임의의 두 점으로 직선을 그리고, 그 직선이 집합에 포함되는지를 확인하면 됩니다.

$x_1, x_2$가 line 위에 그려져 있습니다.

$x = \theta x_1 + (1-\theta)x_2$ $(\theta \in \boldsymbol R)$

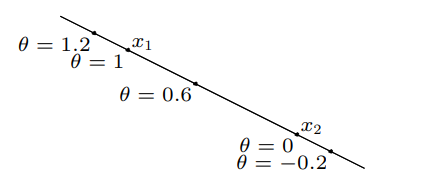
예시로 {$x| Ax=b$}의 선형 방정식 해를 의미합니다.

위 식은 set에 속한 두 점을 linear combination하면서 계수의 합을 1로 제한 했습니다. ($\theta$와 $(1-\theta$)

Convex set

$<convex \ set>$

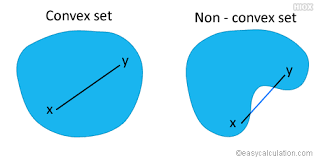
set은 집합을 의미합니다.

어떤 집합(set)이 주어져 있을 때, 이 집합의 원소인 두 점 $x_1$, $x_2$를 잇는 선분이 이 집합에 다시 포함될 때 이 집합을 convex set이라고 부릅니다.

그래서 위의 그림에서 convex set에 해당되는 그림은 왼쪽 그림입니다.

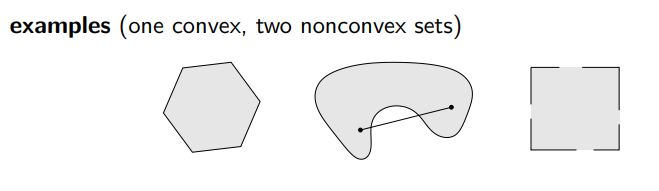
해당 그림에서는 제일 왼쪽만 convex하고 오른쪽 2개는 nonconvex sets임을 알 수 있습니다.

Convex function

$<convex \ function>$

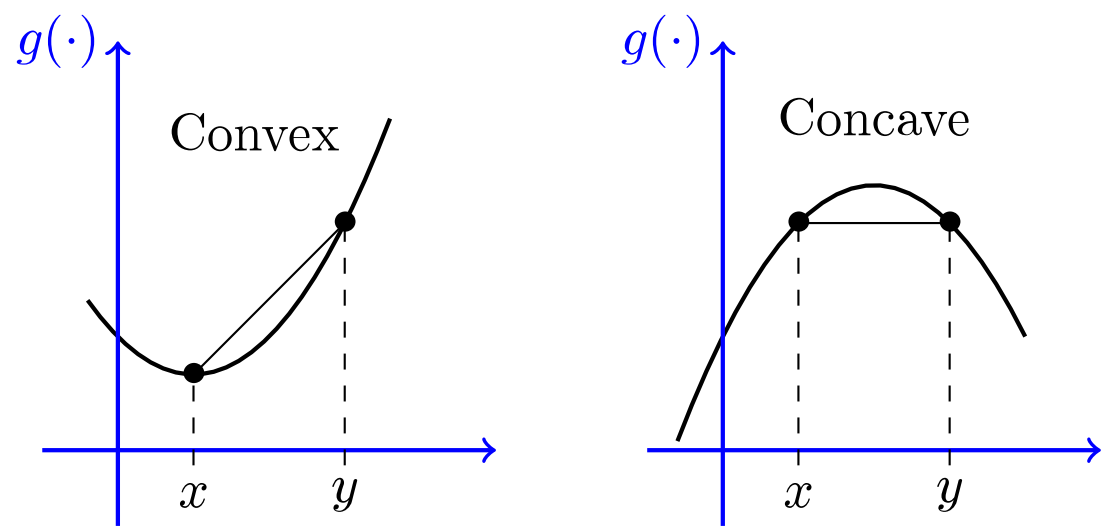
$f: R^n \rightarrow R$ is convex if dom f is a convex set and
$f(\alpha x+(1-\alpha)y) \le \alpha f(x) + (1-\alpha)f(y)$ for all $x,y \in dom \ f, 0 \le \alpha \le 1$

위 정의에서 부등식으로 표현된 조건은 다음과 같은 기하학적 의미를 가집니다.

f의 그래프 상의 임의의 두 점 (x, f(x)), (y, f(y))이 있다고 할 때,

이 두 점을 잇는 선분은 구간 [x, y]에서 그래프보다 크거나 같게 위합니다.

그래서 결국 위의 조건을 만족하는 경우,

f(x)가 convex이고 feasible set이 convex일 때의 경우엔

local minimum이 global minimum이다.

라는 것을 알 수 있습니다.

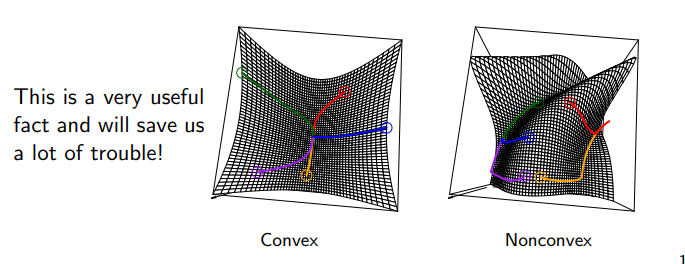
따라서 optimization problem에서는 함수를 convex하게 바꾸는 것, 그러면 global minimum을 찾을 수 있다는 것을 보장 받기 때문에 최적화에서 해당 개념이 중요하다고 볼 수 있습니다.