TIL(Today I Learn) - #6. Data Structure - Tree / Binary Search Tree

트리는 하나의 부모 노드에서 아래로 내려오는 Graph라고 할 수 있습니다.

앞서 보인 큐(Queue), 스택(Stack) 등은 자료구조에서 선형 구조라 한다.
선형 구조란 자료를 구성하고 있는 데이터들이 순차적으로 나열시킨 형태를 의미합니다.
이번에 배울 트리는 비선형 구조입니다. 비선형 구조는 선형구조와는 다르게 데이터가 계층적(혹은 망)으로 구성되어있습니다.
선형구조와 비선형구조의 차이점은 구성형태뿐만 아니라 용도에서도 차이점이 들어나는데요, 선형구조는 자료를 저장하고 꺼내는 것에 초점이 맞춰져 있고, 비선형구조는 표현에 초점이 맞춰져 있습니다. 그렇다면 트리는 무엇을 표현하기 위한 자료구조일까요?

컴퓨터의 directory 구조가 트리의 대표적인 예가 될 수 있습니다. 어떠한 프로그램, 사진, 영상 등을 찾을 때 우리는 폴더에서 폴더로 들어가면서 찾곤 합니다. 이렇게 계층적인 구조를 갖는 것이 트리라 할 수 있습니다. 또 다른 예로는 조직도, 족보 등이 있습니다.

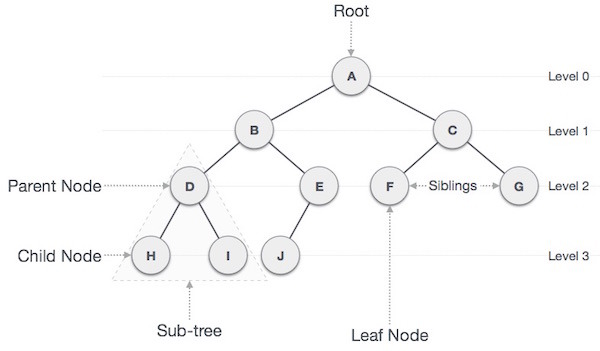
Root Node : 트리 구조에서 최상위에 존재하는 A와 같은 노드
Node : 트리의 구성요소에 해당하는 A,B,C,D,E,F,G,H,I,J와 같은 요소
Edge : 노드와 노드를 연결하는 연결설
Terminal Node(Leaf Node) : 밑으로 또 다른 노드가 연결되어 있지 않은 H,I,J,F,G와 같은 노드
Sub-Tree : 큰 트리(전체)에 속하는 작은 트리
Level : 트리에서 각 층별로 숫자를 매김
Height : 트리의 최고 레벨 (3)

Tree Data Structure 의 Method

• insert()
• get()
• add(data)
• remove()

Binary Tree node 구성 요소

• Data
• Pointer to left child
• Pointer to right child

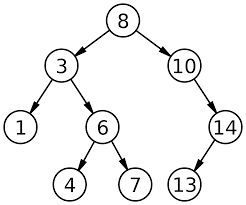
Binary Search Tree

자식을 최대 2개까지만 가질 수 있는 이진 트리,
이진 트리 중에서 이진 검색 트리에 대해 다룹니다.
왜 굳이 이진 검색 트리냐면, 중복 데이터가 없다는 가정 하에 크다와 작다를 쉽게 구분할 수 있기 때문입니다. 따라서 한 번 정렬하면 빠르게 찾을 수 있습니다.